시간 고해상도 라디오존데 관측 자료를 이용한 WRF 모델 행성경계층고도 정확도 평가

1. 서 론

최근 우리나라는 재해기상 대응 및 수자원 확보 등의 목적으로 낙동강 유역에 다목적 보를 설치하였다. 낙동강 유역에 대형 보를 설치함으로써 수표면적과 수심에 큰 변화를 가져온 경우와 같은 대규모의 국토개발에 수반되는 토지이용도의 변화는 행성경계층(PBL, Planetary Boundary Layer)의 기상 변화를 유발한다. PBL은 인간 활동이 이루어지는 하층대기로써 이곳에서는 온도, 습도, 바람 등의 모든 기상요소와 오염물질의 수송과 확산의 변화가 시공간적으로 급속하게 발생한다(Moon et al., 2011). 또한 대기질 모델링에서도 오염물질의 확산에 PBL 고도가 가장 큰 영향을 미치는 요소이다(Kim et al., 1994). PBL 내에서 야간 복사 냉각으로 형성되는 지표역전 강도가 난류로 인해서 어느 정도 해소될 수 있느냐에 따라서 안개의 발생, 대기오염물질의 확산 등이 크게 달라진다는 사실을 고려해 보면 PBL 고도 변화를 정확하게 파악하는 일이 매우 중요하다는 것을 알 수 있다.

PBL 고도는 라디오존데, 수직측풍장비 등을 이용한 고층기상관측을 통하여 산정될 수 있지만 이는 시간과 비용이 많이 요구되는 문제가 있기 때문에 수치모델을 이용하여 산정하기도 한다. 수치모델에서의 아격자 규모 난류 운동 영향은 PBL 모수화를 통해 표현되고 아격자 규모에서 중요한 역할을 하는 난류운동의 난류 혼합에 의해 PBL 내에서의 대기상태와 PBL 고도를 변경 시킬 수 있다. 지금까지 여러 선행연구에서는 수치모델에서 PBL 모수화의 중요성이 강조되어왔다. Bright and Mullen (2002)는 상층역전이 있을 때 난류 혼합이 작으면 차갑고 습하며 얇은 PBL을 모의하고 이것은 결국 부정확한 대류잠재에너지를 생산한다고 하였다. 또한 Braun and Tao(2000)는 PBL 내에서 지나친 난류 혼합은 따뜻하고 건조하며 두꺼운 PBL을 모의한다고 하였다. 특히 Li and Pu (2008)는 PBL 방안이 허리케인 강도와 동반하는 강수 모의에서 구름물리 방안만큼 중요하다고 하였다.

모델에서 제공하는 각각의 PBL 모수화 방안 별로그 특성이 다르기 때문에 PBL 방안에 따른 민감도 연구에 따라 모델링 결과에 차이가 있음을 여러 선행연구에서 제시하였다(Bright and Mullen, 2002; Zhang and Zheng, 2004; Hong et al., 2006; Shin and Hong, 2011; Garcia-Diez et al., 2013). Zhang and Zheng(2004)은 미국 중부를 대상으로 수치 모의한 결과 YSU, ACM2 방안은 MYJ 방안보다 낮 시간 동안 풍속을 낮게 모의하고, MYJ 방안은 저녁시간의 하층제트를 더 강하게 모의한다고 하였다. Hu et al. (2010)은 PBL 내에서의 오염사례를 정확하게 모의하기 위하여 2005년 여름철 텍사스 지역을 대상으로 WRF모델의 PBL 방안을 평가하였다. 그 결과 YSU와 ACM2방안이 낮 시간 동안 하층에서의 강한 연직 혼합 때문에 MYJ 방안보다 높은 기온과 낮은 습도를 모의한다고 하였다. 또한 낮 시간 동안 ACM2는 가장 높은 PBL 고도를 모의하였고 MYJ는 가장 낮은 PBL 고도를 모의하였다. 그러나 전반적으로 모의된 PBL 고도는 관측보다 최고고도가 일찍 나타나고 과소모의 된다고 하였다. Garcia-Diez et al. (2013)도 유럽을 대상으로 민감도 평가를 수행한 결과 주간에 YSU 방안은 ACM2, MYJ 방안보다 PBL 고도를 높게 모의한다고 하였다.

이러한 수치 모델의 PBL 방안 별 민감도 분석에 관한 연구들은 대부분 기온과 풍속 같은 지표면 기상변수와 그 변수들의 연직 구조 특성 분석에 초점을 맞춰 진행되었다. 한편 PBL 방안에 따른 PBL 고도를 분석한 연구가 있다고 하더라도 실제 PBL 고도관측자료는 없이 PBL 방안 별로 비교 하였거나 시간해상도가 낮은 관측 자료를 사용하여 분석 하였다. 또한 국내에서는 관측 PBL 고도를 이용하여 수치모델PBL 고도를 분석하고 평가한 연구가 부족한 실정이다.

본 연구에서는 중규모 기상모델의 PBL 고도 산정방식에 따른 정확도를 평가하기 위하여, PBL 모수화방안 중 가장 많이 사용하고 있는 MYJ (Mellor-Yamada-Janjic) PBL (Janjic, 1990) 방안과 YSU (YonSei University) PBL (Hong et al., 2006) 방안을 대상으로 모델 PBL 고도 정확도를 평가하고자 한다. 현재 우리나라 기상청에서는 백령도, 흑산도, 고산, 포항, 속초에서 일 2회 정규 고층기상관측을 실시하고 있으나 국지규모 기상현상에 활용하기에는 시 · 공간적인 제약이 따른다. 따라서 낙동강 중류에서 3시간 간격으로 수행한 고층기상관측자료로부터 산정된 PBL 고도를 이용하여 평가하고자 한다. 또한 YSU 방안을 대상으로 연직 분석을 통해 PBL 고도 오차원인을 파악하고, PBL 고도 오차를 줄이기 위한 방안으로 라디오 존데 자료를 이용한 자료동화(FDDA, Four-Dimensional Data Assimilation) 실험을 수행하고자 한다.

2. 자료 및 방법

2.1 사례일 및 관측 PBL 고도 산정

국립기상과학원에서는 낙동강 수변 지역의 국지기상 특성을 분석하기 위해 구미보 G4지점(36.241^oN, 128.334^oE)에서 라디오존데를 이용하여 고층기상관측을 수행하였다. 라디오존데 관측은 2014년 8월부터 12월까지 5개월 동안 각 월별 4일씩 수행되었고 고해상도 시간간격의 고층기상관측자료를 얻기 위하여 3시간 간격으로 라디오존데를 비양하였다. 1일 8회[00, 03, 06, 09, 12, 15, 18, 21 LST (Local Standard Time)]에 걸쳐 매달 32회, 총 160회 관측이 이루어졌다. 라디오존데를 이용하여 관측된 기상요소는 기온, 습도, 기압, 풍향, 풍속으로 관측된 기상자료를 이용하여 PBL 고도를 산정하였다. 8월에서 12월까지의 관측 날짜에 대한 실험명을 각각 Exp(8), Exp(9), Exp(10), Exp(11), Exp(12)로 명명 하였다(Table 2).

Table 2.

The configuration of the WRF simulation.

본 연구에서 사용된 관측 PBL 고도는 WRF 모델에서 의미하는 PBL 고도와 일치하도록 연직 혼합이 발생하는 층을 포함하여 유입역이 시작되는 고도까지로 정의하였다(Hu et al., 2010). 관측 PBL 고도는 Parcel 방법을 이용하여 산정하였고, 이를 벌크 리차드슨 수(Ri_b; Bulk richardson number) 방법과 비교하였다. Parcel 방법은 온도, 비습 등의 난류 혼합에 의해 직접적으로 영향을 받는 물리량의 연직 분포로 PBL 고도를 결정하는 방법으로, PBL 내에서는 난류에 의해 열, 수증기, 운동량이 연직으로 균일하게 혼합되므로 상층관측으로부터 얻은 온위와 혼합비의 연직 분포를 이용하여 PBL 고도를 결정할 수 있다(Benkley and Schulman, 1979; Lohou et al., 1998). Parcel 방법을 이용하여 PBL 고도를 산정할 때에는 주간과 야간에 다른 방법을 적용하였다. 주간에는 Lohou et al. (1998)이 제시한 방법을 응용하여 상층 관측으로부터 얻은 기온, 온위, 상당온위의 감률이 가장 크게 나타나는 고도를 PBL 고도로 결정하였다. 그리고 야간에는 지표 안정층의 상단을 PBL 고도로 결정하였다(Kaimal and Finnigan, 1994; Min et al., 1999). Ri_b 방법은 연직시어에 의해 생성되는 난류에 대한 열적으로 생성되는 난류의 비를 이용하여 PBL고도를 산정하는 것으로, 지면으로부터 계산된 Ri_b값이 임계값 0.25를 초과할 때의 고도를 경계층으로 결정한다(Seibert et al., 2000).

2.2 수치 모델 환경 설정

본 연구에서 사용한 기상모델은 NCAR (National Center for Atmospheric Research)에서 개발된 WRF모델 버전 3.4.1을 이용하였다. WRF는 비정역학 모델로 미규모, 중규모 기상 현상을 모의하기에 적합하다. 도메인은 단일 도메인으로 PBL 고도 모의에 있어서 종관 변화를 반영하기 위하여 우리나라 전역을 포함하였다(Fig. 1). 수평해상도는 1.5 km이고 연직 해상도는 지표 부근에 대한 정밀한 모사를 위하여 40개의 시그마 층으로 세분화 하였으며, 모델의 최하층은 0.995σ 레벨로 약 30 m 수준이다.

Fig. 1.

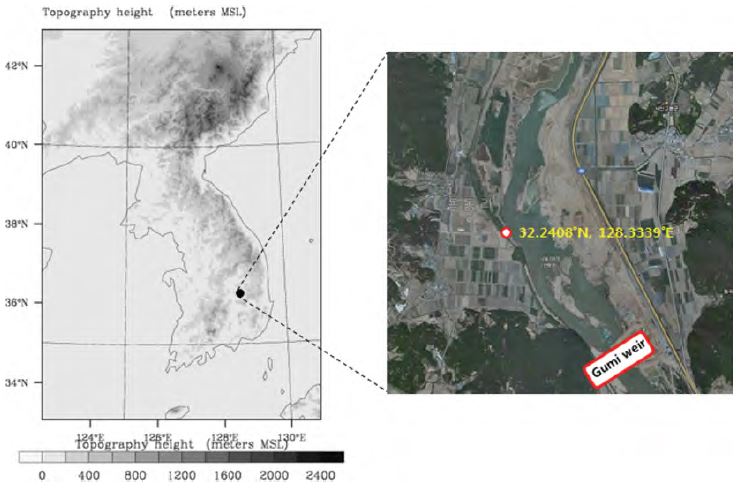
The map of domain for the WRF model. Horizontal grid size of the domain is 1,500 m and closed circle indicates the site of radiosonde observation near the Gumi weir in Nakdong river.

PBL 방안은 기존 연구에서 가장 많이 사용되고 있는 MYJ PBL 방안과 YSU PBL 방안을 이용하였다. MYJ PBL 방안은 국지 1.5차수 국지 종결 방안으로서 TKE (Turbulent Kinetic Energy) 진단 방정식을 이용하여 열과 수분 속을 계산한다. 열과 수분 속을 계산하기 위한 방정식은 혼합 항을 포함하고 있기 때문에 큰 맴돌이 효과를 나타낼 수 있다. MYJ PBL 방안에서 PBL 고도는 TKE 프로파일을 이용하여 결정된다. TKE는 PBL 내에서 가장 크게 나타나기 때문에 TKE가 이미 규정된 값인 0.005 m2 s−2보다 낮은 값으로 감소하는 지점의 높이를 PBL의 상단으로 정의한다(Janjic, 2002). YSU PBL 방안은 비국지 맴돌이 확산 계수를 이용하여 난류 속을 계산한다. YSU PBL 방안은 MRF (Medium Range Forecast) 모델의 PBL 방안을 기반으로 상층 유입효과를 명시적으로 처리하여 개선하였다. PBL 고도는 지표면의 플럭스로 계산된 지표면부근의 온위와 경계층 고도에서의 온위의 역경도항과 지표층과 그 위층의 안정도를 판별하는 Ri_b를 고려하여 계산된다. 지면에서부터 계산된 Ri_b의 임계값이 0.25를 초과할 때의 고도를 PBL의 상단으로 정의한다(Hong and Kim, 2008). 각각의 PBL 방안에서 PBL 고도를 결정하는 방법은 다르지만 이 자체가 각 PBL 방안의 특징이므로 각 방안에 따른 PBL 고도를 이용하였다(Shin and Hong, 2011).

자세한 모델 환경설정은 Table 1에 제시하였으며 수치모의는 각 관측 대상 사례[Exp(8) - Exp(12)]에 24시간의 초기적응시간(spin up time)을 고려하여 수행되었다.

Table 1.

The period of observation and experiment.

2.3 자료동화 및 PBL 고도 평가

YSU PBL 방안을 이용한 실험을 대상으로 PBL 고도 산정에 관여하는 가온위와 풍속의 연직 프로파일을 검증하고, PBL 고도 정확도를 향상시키는 방안으로 라디오존데 자료를 이용한 자료동화를 수행하였다. 사례는 전체 사례 중 종관장 영향을 받지 않고 맑은 날이 지속된 사례인 Exp(11)를 이용하였다. 본 연구에서 사용된 자료동화 기법은 오차를 줄이는데 효율적인 방법인 FDDA (Four-Dimensional Data Assimilation) 방법이다(Stauffer and Seaman, 1990, 1994). FDDA 방법에는 종관장을 따르는 관측치를 이용하여 경계 조건을 변화시키고 격자 형태로 내삽하는 분석 넛징(Analysis nudging)과 관측치를 직접 내삽하는 관측 넛징(Observation nudging)이 있다(Shafran et al., 2000). 본 연구에서는 관측치를 3시간 간격으로 직접 내삽하는 관측 넛징을 사용하였다. FDDA 방법에 활용된 고층관측자료는 5 hPa 간격의 온도, 노점 온도, 풍속, 풍향, 기압, 고도이다. 관측 넛징을 할 때에 넛징 계수가 너무 크면 관측이 모델 내에 너무 강하게 내삽 되어 모델의 불균형을 초래 할 수 있다. 반면 넛징 계수가 너무 작으면 모델 상태의 발달에 아주 작은 영향을 미치게 되어 기상장을 효과적으로 개선하기 어렵다(Stauffer and Seaman, 1990). 따라서 넛징 실험에 대해 최적화된 넛징 계수를 찾기 위해 바람과 기온의 넛징 계수(단위: s⁻¹)를 각각 3.0 × 10⁻⁴, 3.0 × 10⁻¹로 설정하여 실험(이하 넛징 계수 실험)을 수행하였다.

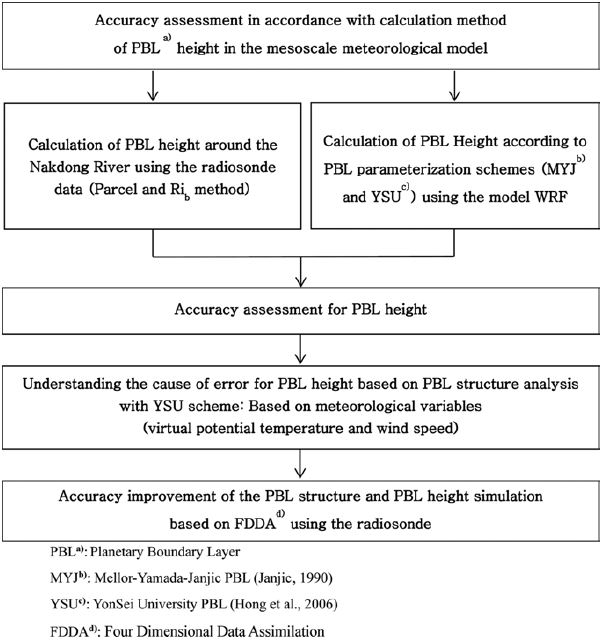
마지막으로 모델에서 산정된 PBL 고도는 관측 PBL 고도를 이용하여 평가되었다. 모델 평가방법으로는 편의(Bias)와 평균 제곱근 오차(RMSE, Root Mean Square Error)를 이용하였다. 본 연구의 전반적인 연구 흐름도는 Fig. 2에 간략하게 나타내었다.

Fig. 2.

Flow chart to simulate the accuracy assessment in accordance with calculation method of PBL height (m) in the mesoscale meteorological model.

3. 결 과

3.1 관측 PBL 고도 특성

Parcel 방법으로 산정된 관측 PBL 고도를 Ri_b 방법의 PBL 고도와 비교하였다. Figure 3은 8월부터 12월[Exp(8) - Exp(12)]까지 산정된 관측 PBL 고도를 시간(LST, Local Standard Time) 별로 나타낸 것이다. 붉은 막대는 Parcel 방법(이하 OBS-Pa), 푸른 막대는 Ri_b 방법(이하 OBS-Ri)으로 산정된 PBL 고도이고 점선은 각 방법의 평균을 나타낸 것이다.

Fig. 3.

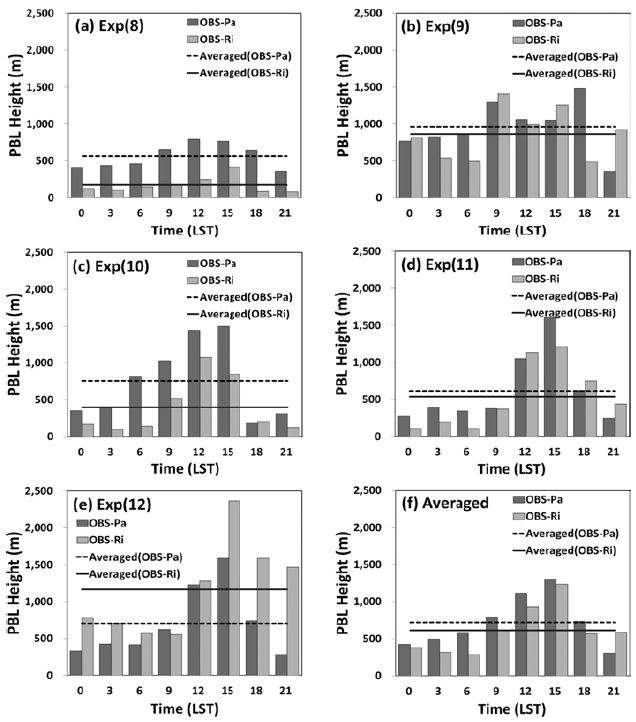
Mean diurnal variation of observed PBL height (m) using two different PBL height (m) calculation method (Parcel and Rib method) and averaged PBL height (m).

OBS-Pa과 OBS-Ri에 따라 산정된 PBL 고도는 전반적으로 낮 시간에 상승하고 저녁시간에 하강하는 일 변동성을 유사하게 나타냈다. 이 중 EXP(12)에서 두 방법간 평균 PBL 고도 차이가 가장 크게 나타났고, 반면 EXP(11)에서는 그 차이가 74 m로 두 방법간 PBL 고도가 비슷하였다. EXP(12)는 OBS-Pa가 OBS-Ri 보다 PBL 고도를 460 m 낮게 산정하였고, EXP(12)를 제외한 나머지 사례에서는 OBS-Pa가 OBSRi보다 PBL 고도를 높게 산정하였다. 전체 사례일 평균을 나타낸 Fig. 3f에서도 두 방법 모두 1500 LST에 PBL 고도가 가장 높게 형성되었고, 저녁에는 하강하는 패턴을 나타냈다. 그러나 2100 LST를 제외한 모든 시간에서 OBS-Ri는 OBS-Pa보다 PBL 고도를 낮게 산정하는 경향을 보였다. 0600 LST에 OBS-Pa는 1,115 m이고 OBS-Ri는 935 m로 그 차이가 299 m로 가장 크게 나타났고 1500 LST에 OBS-Pa와 OBS-Ri는 각각 1,302 m, 1,240 m로 그 차이가 62 m로 가장 작게 나타났다. OBS-Pa의 평균 PBL 고도는 721 m이고 OBS-Ri은 평균 PBL 고도는 615 m로 OBS-Pa 방법이 평균 106 m 정도 PBL 고도를 높게 산정하는 경향을 나타냈다(Fig. 3f).

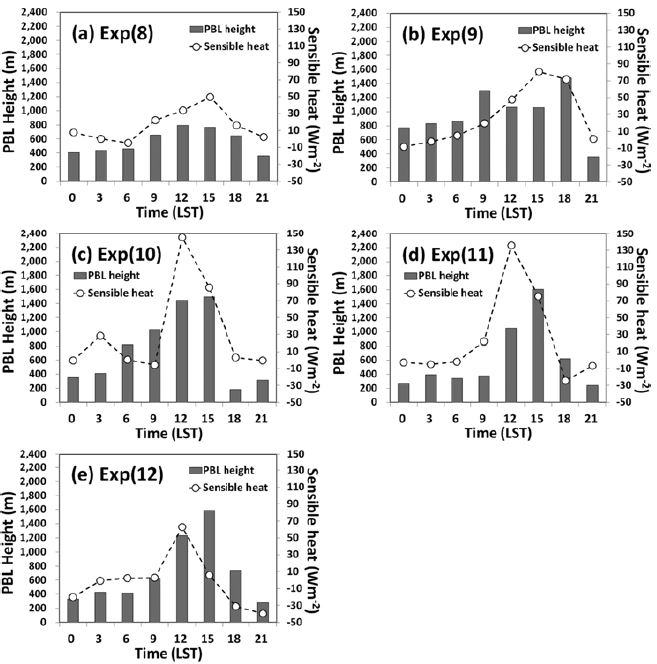
일반적으로 육지나 해양 위에서 주간의 대기 혼합층은 종관 상태와 무관하게 표층 현열속이 강한 지역에서 높게 발달하고 무차원화 된 현열속은 고도에 따라 선형적으로 감속하여 혼합층의 상부에서 0에 이르기 때문에, 혼합층 고도와 지표면 현열속과는 밀접한 관계가 있다고 하였다(Kwon et al., 1998). 따라서 지표면 현열속과 PBL 고도 발달의 관계를 알아보기 위해 Fig. 4에 지표면 현열속과 OBS-Pa로 산정된 PBL 고도를 나타내었다. 지표면 현열속은 낙동강 구미보 G4 플럭스 타워(Kang et al. (2015)의 Fig. 1b 참조)의 10 Hz 자료를 이용하였다. PBL 고도는 밤시간에 낮았다가 지표면 가열이 강한 낮 시간에 가장 잘 발달하고 밤시간에 다시 낮아지는 일변화 패턴을 보였다. 특히 낮 시간의 높은 지표면 현열속은 강한 열적 난류를 발달시켜 PBL 고도를 높게 발달시키는 것을 확인할 수 있었다. PBL 고도의 평균은 Exp(9)가 가장 높았고 Exp(10), Exp(12), Exp(11), Exp(8) 순으로 낮게 나타났다. 낮시간 현열속이 가장 높았던 EXP(11)는 1500 LST에 PBL 고도를 1,605 m로 제일 높게 형성하였다. Exp(8)의 PBL 고도는 1200 LST에 792.5 m까지 발달하였으나 다른 사례 보다 높게 발달하지 못하였다. Exp(8)은 강수로 인해 지표면에서 열원이 부족하였으며 그 결과 공기가 온도 성층화를 이루면서 PBL 고도가 성장하지 못한 것으로 보였다. 더불어 여름철에 PBL 고도가 낮은 이유는 여름철에 공기가 지표면뿐만 아니라 높은 고도에 이르기까지 전체적으로 데워져 지표면 현열속이 봄이나 가을에 비해 그리 크지 않기 때문이라고 하였다(Min et al., 1999). 사례별 낮시간의 현열속을 살펴보면 EXP(8)의 현연속은 29.7 W m⁻²이고, Exp(9)는 42.6 W m⁻², Exp(10)은 51.3 W m⁻², Exp(11)은 52.3 W m⁻²로 Exp(8)이 보다 낮게 나타났다. Exp(12)는 Exp(11)보다 낮시간 동안 낮은 현열속을 보였지만 시베리아 고기압 하에서 찬 기단이 상부에 유입되어 불안정이 유도되고 혼합이 촉진되어 높은 PBL 고도를 형성하였다.

Fig. 4.

Mean diurnal variation of observed PBL height (m; OBS-Pa) and surface sensible heat flux (W m−2).

3.2 PBL 고도 평가

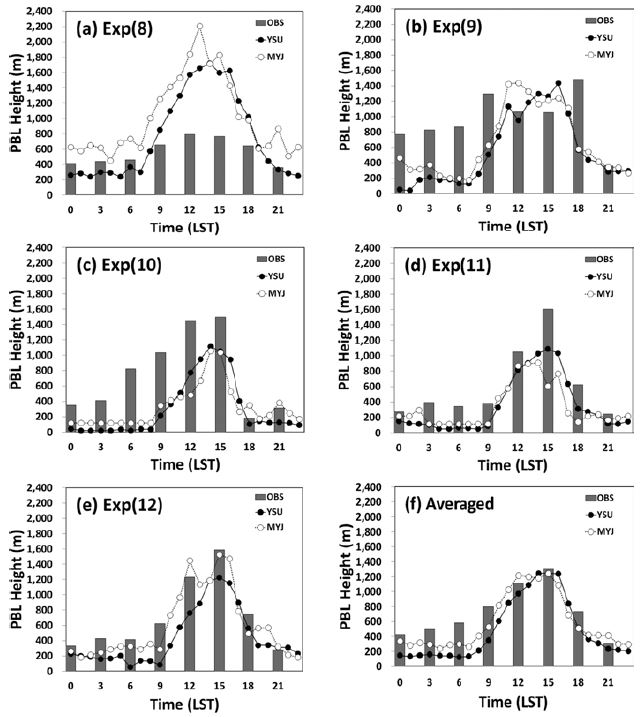
MYJ와 YSU PBL 방안을 이용하여 모델에서 산정된 PBL 고도의 오차를 분석하기 위하여 Fig. 5에 모델에서 산정된 PBL 고도와 관측 PBL 고도를 사례별로 시계열로 나타내었다. 그래프에서 막대형은 관측 PBL 고도를 나타낸 것이고 꺾은 선형은 YSU(●) PBL방안(이하 YSU)과 MYJ(○) PBL 방안(이하 MYJ) 결과를 각각 나타낸 것이다. 또한 사례 별 모델 RMSE(m)와 Bias (m)를 Table 3에 나타내었고, 전 기간, 주간(0700-1800 LST) · 야간(1900-0600 LST) 및 날씨 별(맑은 날, 흐린 날, 강수일, 안개일)로 세분화하여 나타내었다.

Fig. 5.

Time series of the PBL height (m) calculated from the five experiments and their average.

Table 3.

RMSE and Bias based on PBL scheme (MYJ, YSU), experiment [Exp(8), Exp(9), Exp(10), Exp(11), and Exp(12)), weather conditions (clear, cloudy, rainy, and misty days), and time (day and night time).

Figure 5의 모든 사례[Exp(8) - Exp(12)]에서 YSU, MYJ 모두 관측과 마찬가지로 낮 시간에는 PBL 고도를 높게 형성하였고 저녁 시간에는 하강하는 일 변동성을 잘 모의하였다. 두 PBL 방안 중 PBL 고도 최대치가 나타나는 시점은 MYJ보다 YSU가 관측과 보다 유사하게 모의하였다. 그러나 두 방안 모두 낮 시간 동안 PBL 고도의 오차가 크게 나타났다. Exp(8)의 경우 낮 시간 동안 MYJ, YSU 두 방안 모두 PBL 고도를 과대 모의하였고 이 때의 Bias는 YSU는 546.1 m, MYJ는 762.2 m를 나타내었다. 특히 1200 LST에 각 방안의 PBL 고도는 관측과 MYJ는 1,046 m, YSU는 780 m의 차이를 보였다. Exp(9)는 주간에 전반적으로 과소 모의를 하였으나 1500 LST에는 두 방안모두 과대 모의를 하였다. YSU의 주간 Bias는 −401.8 m를 MYJ는 −257.3 m를 나타내었다. 나머지 사례[Exp(10) - Exp(12)]에서도 주간에 두 PBL 방안 모두 Bias가 음의 값으로 PBL 고도를 과소 모의하였다. Exp(10) - Exp(12) 세 사례는 Hu et al. (2010)의 연구에서 전반적으로 모의된 PBL 고도는 관측보다 과소 모의된다고 한 결과와 부합한다. 일반적으로 선행연구에서는 YSU PBL 방안이 MYJ PBL 방안보다 낮 시간 동안 PBL 고도를 높게 모의한다고 하였다(Hu et al., 2010; Garcia-Diez et al., 2013). 그러나 본 연구에서는 Exp(8)과 Exp(12)를 제외한 모든 사례에서는 MYJ보다 YSU가 낮 시간 동안 PBL 고도를 보다 높게 모의하여 선행연구와 다른 양상을 보였다. Exp(8)의 경우에는 주간에 YSU가 MYJ 보다 PBL 고도를 낮게 모의하였고 RMSE는 YSU가 MYJ보다 252.9 m 작게 나타내었다. 반면 Exp(11)은 주간에 YSU가 MYJ보다 PBL 고도를 높게 모의하였고 이 때의 YSU와 MYJ의 RMSE는 각각 551.5 m와 843.2 m로 YSU의 오차가 작게 나타났다.

밤 시간 동안의 PBL 고도를 살펴보면, Exp(8)의 MYJ를 제외한 모든 사례에서 밤 시간 동안 관측보다 PBL 고도를 과소 모의하는 경향을 나타냈다. 자정에 가까워질수록 실제 역전 층의 발달에 의하여 성장하는 PBL 고도를 두 방안 모두 모의하지 못하였고 지표 층에 낮게 거의 일정하게 모의하였다. 특히, 저녁시간에 YSU는 MYJ보다 PBL 고도를 보다 낮게 모의하였다. YSU는 야간의 안정한 대기에서 연직 혼합을 덜 발달시키고 이를 개선하기 위하여 지속적으로 노력 중에 있다(Hong, 2010).

YSU, MYJ의 날씨 별 PBL 고도 오차를 살펴보았다(Table 3). 날씨 별로 분석 하였을 때도 주간에는 YSU의 RMSE가 작았고 야간에는 MYJ가 작았다. 맑은 날의 낮 시간 동안의 RMSE를 살펴보면 YSU는 669.1 m이고 MYJ는 823.6 m 수준이고 야간에는 각각 380.6 m, 366.9 m 수준으로, 주간에는 YSU의 RMSE가 작았고 야간에는 MYJ의 RMSE가 작았으나 그 차이는 미미하였다. 강수일에는 두 방안모두 과대모의를 보였고 각 방안의 Bias는 YSU는 200.1 m, MYJ는 1,054.2 m를 나타내었다. 이러한 강수일의 오차로 인하여 강수일이 다수 포함되어 있는 Exp(8)의 PBL 고도는 관측과 차이가 크게 나타났다.

3.3 PBL 고도 정확도 향상

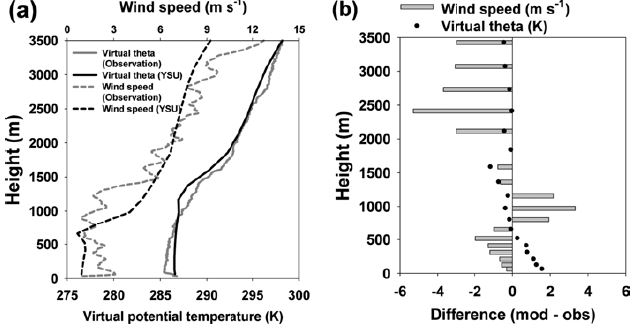
Exp(11)에서 YSU 방안을 대상으로 PBL 고도 산정에 관여하는 기상변수인 가온위와 풍속의 연직 분포를 검증하였다. Exp(11)은 종관장의 영향이 크지 않고 맑은 날이 지속된 사례이다. Exp(11)에서 2014년 11월 18일은 PBL 고도의 오차가 작은 사례이고 2014년 11월 20일은 오차가 큰 사례로 이 사례들의 PBL 고도를 Fig. 6에 시계열로 나타내었다. PBL 고도 오차가 작은 사례(2014년 11월 18일)의 일 평균 Bias는 88.8 m 수준으로 과대 모의되었고, RMSE는 189.1 m수준이었다. 2014년 11월 20일 사례의 경우에는 Bias가 −418.7 m로 PBL 고도는 과소 모의되었고 RMSE는 488.2 m 수준으로 나타났다. 2014년 11월 18일과 20일 1500 LST의 가온위와 풍속의 연직 프로파일을 Fig. 7과 Fig. 8에 각각 나타내었다. 이 때 PBL 고도 Bias는 2014년 11월 18일에는 15.2 m이었고 2014년 11월 20일에는 −418.7 m였다. 약 1 km 고도에서 온위와 풍속이 급격하게 변하기 때문에 1 km를 기준으로 상 · 하층 오차를 분석하였다. 2014년 11월 18일 1500 LST에 풍속은 전 층에서 전반적으로 과대 모의를 보였고 1 km 이하와 이상에서의 RMSE는 각각 2.9m s⁻¹와 1.6 m s⁻¹로 1 km 이하에서의 오차가 더 크게 나타났다. 온위는 풍속과 반대로 전 층에 걸쳐 과소모의를 보였으며 1 km 이하와 이상에서의 RMSE는 각각 0.7 K와 1.5 K로 하층보다 상층에서의 오차가 컸다. 2014년 11월 20일 1500 LST에 풍속은 전반적으로 과소 모의가 되었으나 1 km 고도 전후에서 과대모의를 하고 상층으로 갈수록 오차가 커지는 경향을 보였다. 1 km 이하에서의 가온위 Bias는 0.6 K로 과대모의 되었고 1 km 이상의 고도에서는 Bias가 −0.4 K로 과소 모의 되었다. 관측 가온위의 연직 구조가 하층에서 상층까지 거의 일정하다가 상층에서 급격한 감률을 보이는 일반적인 온위 연직 구조 일 때, 모델이 보다 연직 구조 오차를 작게 모의하였고 PBL 고도의 정확도도 보다 크게 나타났다. 또한 하층에서 풍속의 절대 오차와 상관없이 가온위와 풍속의 연직 구조가 관측과 비슷할 때 PBL 고도 모의 오차가 작게 나타났다.

Fig. 6.

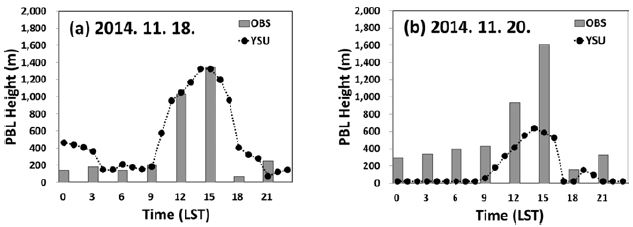
PBL height (m) on (a) a high accuracy case of 18 November 2014 and (b) a low accuracy case of 20 November 2014.

Fig. 7.

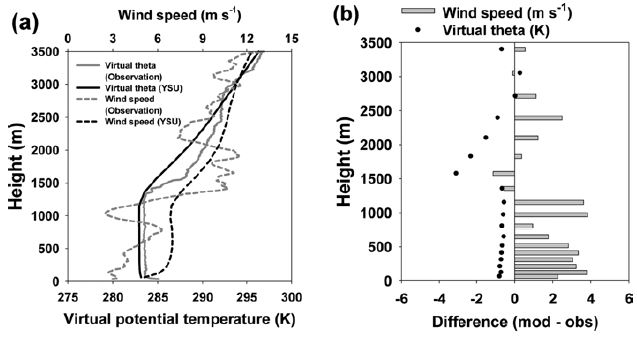
(a) Boundary layer profiles of observed and simulated (YSU scheme) virtual potential temperature and wind speed and (b) their difference at 1500 LST on 18 November 2014.

Fig. 8.

Same as Fig. 7, except for at 1500 LST on 20 November 2014.

앞선 결과로부터 모델에서 PBL 고도의 오차를 줄이기 위해서는 PBL 내의 가온위와 풍속의 연직구조를 정확하게 모의 것이 중요하다고 판단되었다. 한편 수치모델에서 라디오존데 자료를 자료동화에 사용함으로써 단기 예측성을 향상시킨다고 하였다(Hwang et al., 2011; Lim et al., 2014). 따라서 가온위와 풍속을 보다 정확하게 모의하고자 하고자 PBL 고도의 오차가 컸던 2014년 11월 20일을 대상으로 FDDA 방법을 이용하여 넛징 계수 실험을 추가적으로 수행하였다. 넛징 계수를 3.0 × 10⁻⁴로 설정한 실험인 YSU_FDDA_1과 3.0 × 10⁻¹로 설정한 실험인 YSU_FDDA_2의 1500 LST의 풍속과 가온위 연직 프로파일을 Fig. 9에 각각 나타내었다. 풍속의 연직 분포 분석 결과, FDDA를 적용한 두 실험 모두 풍속은 여전히 하층에서 관측보다 과소 모의하였으나, 두 실험 모두 300 m 이하에서의 오차가 줄었고 YSU보다 풍속이 상층(약 1 km)으로 갈수록 줄어들었다. 그 중 YSU_FDDA_2가 YSU_FDDA_1보다 풍속의 연직 구조를 관측과 더욱 비슷하게 모의하였다. 가온위의 경우에는 FDDA를 적용했음에도 불구하고 두 실험 모두 여전히 하층에서 과대모의를 보였으나 YSU_FDDA_2는 상층으로 갈수록 오차가 줄어들었다. 연직 분포 분석을 수행한 1500 LST의 관측 PBL 고도는 1,610 m이었고 YSU_FDDA_1의 경우에는 575.4 m, YSU_FDDA_2의 경우에는 998.8m로 YSU_FDDA_2의 경우에 YSU_FDDA_1보다 PBL 고도를 426.5 m 정도 높게 모의하여 관측과 보다 비슷하게 모의 하였다. Figure 10은 본 사례의 관측과 모델의 PBL 고도를 시계열로 나타낸 것이다. 또한 각각의 실험에 대한 Bias와 RMSE를 Table 4에 제시하였다. 저녁시간의 YSU_FDDA_1과 YSU_FDDA_2의 PBL 고도 Bias는 각각 −278.0 m와 −259.5 m로 YSU 실험과 비슷한 수준(−278.0m)으로 여전히 야간의 오차는 개선되지 않았다. 그러나 YSU_FDDA_2의 경우에는 주간 Bias가 −330.2 m로 YSU의 −516.8 m보다 개선되었다. 그러나 YSU_FDDA_1의 경우, 0900 LST 이후에도 PBL 고도를 YSU와 비슷한 수준으로 모의하였지만 관측자료를 넛징하였음에도 불구하고 YSU 보다 오차가 증가하였고 여전히 과소모의 하는 경향을 보였다. 세부적으로 1200 LST에는 372 m로 관측보다 566 m 낮게 모의하였고 1500 LST에는 575 m로 관측보다 1,035 m 낮게 모의하였다. 또한 1800 LST 이후 에는 YSU보다 PBL 고도 오차가 증가하였다. YSU_FDDA_2의 경우에도 여전히 관측보다는 과소 모의를 하였지만 1200 LST의 PBL 고도는 367 m로 관측과 301 m 정도의 차이를 보였다. 또한 1500 LST에는 999m로 관측보다 611 m 정도 과소 모의를 보였으며 1800 LST에도 YSU_FDDA_2는 94 m로 YSU (20 m)와 YSU_FDDA_1 (20 m)보다 개선됨을 보였다. YSU_FDDA_1은 YSU_FDDA_2에 비해 넛징 계수가 너무 작기 때문에 모델 상태의 발달에 아주 작은 영향을 미치게 되어 기상장을 효과적으로 개선하기 어려운 것으로 판단된다.

Fig. 9.

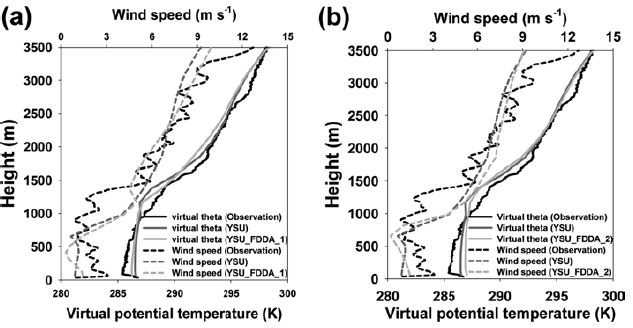
Boundary layer profiles of observed and simulated virtual potential temperature and wind speed from (a) YSU_FDDA_1 and (b) YSU_FDDA_2 experiments at 1500 LST on 20 November 2014.

Fig. 10.

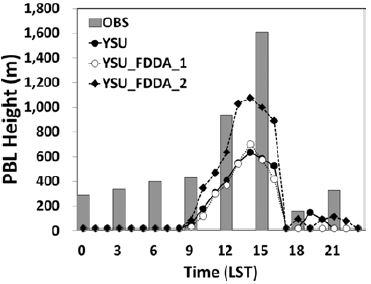
Observed and simulated PBL height (m) before (YSU) and after the Four-Dimensional Data Assimilation (YSU_FDDA_1 and YSU_FDDA_2) on 20 November 2014.

Table 4.

RMSE, and Bias before (YSU) and after the Four-Dimensional Data Assimilation (YSU_FDDA_1 and YSU_FDDA_2) on 20 November 2014.

4. 토 의

본 연구에서는 낙동강 수변지역에서 관측한 시간 고해상도 라디오존데 자료를 이용하여 WRF 모델의 MYJ, YSU PBL 방안에 따른 PBL 고도 정확도를 평가하였다. 또한 YSU PBL 방안을 대상으로 라디오존데 자료를 이용하여 FDDA 수행하였고 이를 통해 PBL 고도의 정확도를 향상시키고자 하였으며 다음과 같은 결과를 얻었다.

라디오존데 자료를 이용하여 관측 PBL 고도를 산정한 결과 Exp(8) - Exp(12)의 평균 PBL 고도는 OBSPa 방법의 경우에는 721 m, OBS-Ri 방법의 경우에는 평균 PBL 고도는 615 m로 OBS-Pa 방법이 PBL 고도를 높게 산정하는 경향을 보였으나 일 변화 패턴은 비교적 잘 일치하였다. PBL 고도는 지표면 현열속이 강한 낮 시간에는 강한 열적 난류를 발달시켜 PBL 고도를 높게 형성시켰고 현열속이 약해짐에 따라 낮아지는 일변화 패턴을 보였다. 이 중 Exp(8)은 강수로 인한 지표면에서의 열원 부족으로 인해 PBL 고도를 낮게 발달시켰고, Exp(12)는 시베리아 고기압 하에서 찬 기단이 상부에 유입해 불안정이 유도되고 혼합이 촉진되어 PBL 고도를 높게 발달시켰다. 이러한 PBL 고도 특징의 결과는 Min et al. (1999), Kwon et al. (2001)과 유사한 결과를 나타내었다.

WRF 모델에서 YSU, MYJ 방안을 이용하여 PBL 고도를 산정하였을 때 Exp(8) - Exp(12)의 모든 사례에서 두 방안 모두 일 변동 특성은 잘 모의하였다. 그러나 YSU 방안과 MYJ 방안의 주간 전체 Bias는 각각 −251.3 m, −124.4 m로 과소 모의를 보였고 각각의 RMSE는 732.4 m, 890.2 m로 MYJ 방안의 오차가 157.6 m 정도 크게 나타났다. 주간에 PBL 방안에 따른 결과 차이는 크진 않지만 전반적으로 YSU 방안을 이용하였을 때 RMSE가 MYJ보다 작게 나타났다. 주간 두 방안 모두 과소 모의 되는 결과는 Hu et al. (2010)의 연구에서 모의된 PBL 고도는 관측보다 과소 모의 된다는 결과와 같은 결과이다. 반면, Hu et al. (2010) 등의 연구에서는 YSU PBL 방안이 MYJ PBL 방안보다 낮 시간 동안 PBL 고도를 높게 모의한다고 하였으나 본 연구에서는 사례별로 다른 양상을 나타냈다. 야간에는 두 방안 모두 PBL 고도를 과소 모의하였다. 특히 YSU 방안은 낮은 연직 혼합에 의해 MYJ 방안보다 PBL 고도를 낮게 모의하였다. 날씨 별로 분석한 결과에서는 맑은 날과 흐린 날, 강수일 모두 YSU 방안이 MYJ 방안보다 낮은 RMSE를 나타냈다.

마지막으로 YSU 방안의 Exp(11) 사례에 대하여 라디오존데 자료를 이용한 관측 넛징을 수행함으로써 PBL 고도의 오차를 어느 정도 줄일 수 있었다(Table 4). 그러나 YSU_FDDA_1, YSU_FDDA_2 두 실험 모두, 고층기상관측 자료 동화 효과에 따른 야간 PBL고도의 정확도 향상 효과는 미미하였다. 반면, YSU_FDDA_2를 통해서 관측 넛징이 주간 PBL 고도 오차감소에는 긍정적인 결과를 나타내는 것을 확인하였다. 한편, YSU_FDDA_1의 경우에는 주간에도 관측 넛징을 수행하기 전인 YSU와 비슷한 결과를 나타냈으며 심지어 오차가 증가하는 경우도 존재했다. 넛징 계수가 너무 작으면 모델 상태의 발달에 아주 작은 영향을 미치게 되어 기상장을 효과적으로 개선하기 어렵기 때문에 오차 개선이 어려운 것으로 판단된다. 이러한 결과는 관측 넛징을 할 때에 적절한 넛징 계수선정이 PBL 고도 모의에 중요함을 시사한다.

향후 다양한 사례와 다양한 PBL 모수화 방안을 이용한 추가적인 모델 PBL 고도 평가가 필요하다. 또한 모델에서의 PBL 고도를 정확하게 모의하기 위한 다양한 방법의 자료동화 등의 초기 입력자료 개선 노력이 지속적으로 필요할 것이다.

Acknowledgments

본 연구는 국립기상과학원 연구개발사업 “기상업무 지원기술개발연구”의 일환으로 수행되었습니다.

REFERENCES

• Benkley, C. W., and L. L. Schulman, (1979), Estimating hourly mixing depths from historical meteorological data, J. Appl. Meteorol., 18, p772-780. [https://doi.org/10.1175/1520-0450(1979)018<0772:EHMDFH>2.0.CO;2]
• Braun, S. A., and W.-K. Tao, (2000), Sensitivity of high-resolution simulation of hurricane Bob (1991) to planetary boundary layer parameterization, Mon. Wea. Rev., 128, p3941-3961. [https://doi.org/10.1175/1520-0493(2000)129<3941:SOHRSO>2.0.CO;2]
• Bright, D. R., and S. L. Mullen, (2002), The sensitivity of the numerical simulation of the southwest monsoon boundary layer to the choice of PBL turbulence parameterization in MM5, Wea. Forecasting, 17, p99-114. [https://doi.org/10.1175/1520-0434(2002)017<0099:TSOTNS>2.0.CO;2]
• Chen, F., and J. Dudhia, (2001), Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part : Model implementation and sensitivity, Mon. Wea. Rev., 129, p569-585. [https://doi.org/10.1175/1520-0493(2001)129<0569:CAALSH>2.0.CO;2]
• Chou, M.-D., and M. J. Suarez, (1994), An efficient thermal infrared radiation parameterization for use in general circulation models, NASA Technical Memorandum, 104606, p85.
• Garcia-Diez, M., J. Fernandez, L. Fita, and C. Yague, (2013), Seasonal dependence of WRF model biases and sensitivity to PBL schemes over Europe, Quart. J. Roy. Meteor. Soc, 139, p501-514. [https://doi.org/10.1002/qj.1976]
• Hong, S.-Y., (2010), A new stable boundary-layer mixing scheme and its impact on the simulated East Asian summer monsoon, Quart. J. Roy. Meteor. Soc., 136, p1481-1496. [https://doi.org/10.1002/qj.665]
• ______, Y. Noh, and J. Dudhia, (2006), A new vertical diffusion package with an explicit treatment of entrainment processes, Mon. Wea. Rev., 134, p2318-2341. [https://doi.org/10.1175/MWR3199.1]
• ______, and S.-W. Kim, (2008), Stable boundary layer mixing in a vertical diffusion scheme, In 18th Symposium on Boundary Layers and Turbulence, B 16.
• Hu, X.-M., J. W. Nielsen-Gammon, and F. Zhang, (2010), Evaluation of three planetary boundary layer schemes in the WRF model, J. Appl. Meteor. Climatol., 49, p1831-1844. [https://doi.org/10.1175/2010JAMC2432.1]
• Hwang, Y. J., J. C. Ha, Y. H. Kim, K. H. Kim, E. H. Jeon, and D. E. Chang, (2011), Observing system experiments using KLAPS and 3DVAR for the upper-air observations over the south and west sea during ProbeX-2009, Atmosphere, 21, p1-16, (in Korean with English abstract).
• Janjic, Z. I., (1990), The step-mountain coordinate: physical package, Mon. Wea. Rev., 118, p1429-1443. [https://doi.org/10.1175/1520-0493(1990)118<1429:TSMCPP>2.0.CO;2]
• ______, (2002), Nonsingular implementation of the Mellor- Yamada level 2.5 scheme in the NCEP Meso model, NCEP office note, 437, p61.
• Kaimal, J. C., and J. J. Finnigan, (1994), Atmospheric Boundary Layer Flows: Their Structure and Measurement, Oxford University Press, p289.
• Kang, M., Y.-K. Lim, C. Cho, K. R. Kim, J. S. Park, and B.-J. Kim, (2015), The sensitivity analyses of initial condition and data assimilation for a fog event using the Mesoscale Meteorological Model, J. Korean Earth Sci. Soc., 36, p567-579, (in Korean with English abstract). [https://doi.org/10.5467/JKESS.2015.36.6.567]
• Kim, Y.-K., J.-H. Hong, and B.-I. Jeon, (1994), A study on the distribution of air pollutant concentration according to micrometeorological characteristics, Atmosphere, 3, p31-38, (in Korean with English abstract).
• Kwon, B. H., B. Benech, D. Lambert, P. Durand, A. Druilhet, H. Giordani, and S. Planton, (1998), Structure of the marine atmospheric boundary layer over an oceanic thermal front: SEMAPHORE experiment, J. Geophys. Res., 103, p25159-25180. [https://doi.org/10.1029/98JC02207]
• ______, K.-D. Min, and D.-S. Kim, (2001), Development of the atmospheric mixed layer observed in Kyungpook province, J. Korean Meteor. Soc., 37, p31-38, (in Korean with English abstract).
• Li, X., and Z. Pu, (2008), Sensitivity of numerical simulation of early rapid intensification of hurricane Emily (2005) to cloud microphysical and planetary boundary layer parameterization, Mon. Wea. Rev., 136, p4819-4838. [https://doi.org/10.1175/2008MWR2366.1]
• Lim, K.-S. S., and S.-Y. Hong, (2010), Development of an effective double-moment cloud microphysics scheme with prognostic cloud condensation nuclei (CCN) for weather and climate models, Mon. Wea. Rev., 138, p1587-1612. [https://doi.org/10.1175/2009MWR2968.1]
• Lim, Y. K., S. K. Song, and S. O. Han, (2014), Data assimilation effect of mobile rawinsonde observation using unified model observing system experiment during the summer intensive observation period in 2013, J. Korean Earth Sci. Soc., 35, p215-224, (in Korean with English abstract). [https://doi.org/10.5467/JKESS.2014.35.4.215]
• Lohou, F., B. Campistron, A. Druilhet, P. Foster, and J. P. Pages, (1998), Turbulence and coherent organizations in the atmospheric boundary layer: a radar-aircraft experimental approach, Bound.-Layer Meteor., 86, p147-179. [https://doi.org/10.1023/A:1000613232592]
• Min, K. D., S. H. Kim, K. E. Kim, and B. H. Kwon, (1999), Seasonal and local characteristics of atmospheric mixed layer over Kyungpook province, J. Korean Meteor. Soc., 35, p539-548, (in Korean with English abstract).
• Mlawer, E. J., S. J. Taubman, P. D. Brown, M. J. Iacono, and S. A. Clough, (1997), Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated- k model for the longwave, J. Geophys. Res., 102, p16663-16682. [https://doi.org/10.1029/97JD00237]
• Moon, N., S. Kim, and J. Seo, (2011), Sensibility study for PBL Scheme of WRF-CMAQ, J. Korean Soc. Atmos. Environ., 27, p791-804, (in Korean with English abstract). [https://doi.org/10.5572/KOSAE.2011.27.6.791]
• Seibert, P., F. Beyrich, S.-E. Gryning, S. Joffre, A. Rasmussen, and P. Tercier, (2000), Review and intercomparison of operational methods for the determination of the mixing height, Atmos. Environ., 34, p1001-1027. [https://doi.org/10.1016/S1352-2310(99)00349-0]
• Shafran, P. C., N. L. Seaman, and G. A. Gayno, (2000), Evaluation of numerical predictions of boundary layer structure during the Lake Michigan Ozone Study, J. Appl. Meteorol., 39, p412-426. [https://doi.org/10.1175/1520-0450(2000)039<0412:EONPOB>2.0.CO;2]
• Shin, H. H., and S. Y. Hong, (2011), Intercomparison of planetary boundary-layer parameterizations in the WRF model for a single day from CASES-99, Bound.-Layer Meteor., 139, p261-281. [https://doi.org/10.1007/s10546-010-9583-z]
• Stauffer, D. R., and N. L. Seaman, (1990), Use of fourdimensional data assimilation in a limited-area mesoscale model. Part I: experiments with synoptic scale data, Mon. Wea. Rev., 118, p1250-1277. [https://doi.org/10.1175/1520-0493(1990)118<1250:UOFDDA>2.0.CO;2]
• ______, and ______, (1994), On multi-scale four-dimensional data assimilation, J. Appl. Meteorl., 33, p416-434. [https://doi.org/10.1175/1520-0450(1994)033<0416:MFDDA>2.0.CO;2]
• Zhang, D.-L., and W.-Z. Zheng, (2004), Diurnal cycles of surface winds and temperatures as simulated by five boundary layer, J. Appl. Meteorol., 43, p157-169. [https://doi.org/10.1175/1520-0450(2004)043<0157:DCOSWA>2.0.CO;2]