도시 협곡에서 수목이 흐름과 스칼라 물질 확산에 미치는 영향
Abstract
In this study, the effects of trees on flow and scalar dispersion in an urban street canyon were investigated using a computational fluid dynamics (CFD) model. For this, we implemented the drag terms of trees to the CFD model, and compared the CFD-simulated results to the wind-tunnel results. For comparison, we considered the same building configuration as the wind-tunnel experiment. The trees were located at the center of street canyon with the aspect ratio (defined as the ratio of the street width to the building height) of 1. First, the flow characteristics were analyzed in the tree-free and high-density tree cases and the results showed that the CFD model reproduced well the flow pattern of the wind-tunnel experiment and reflected the drag effect of trees in the street canyon. Then, the dispersion characteristics of scalar pollutants were investigated for the tree-free, low-density tree and medium-density tree cases. In the tree-free case, the nondimensionalized concentration distribution simulated by the CFD model was quite similar to that in the wind-tunnel experiment in magnitude and pattern. The correlation coefficients between the measured and simulated concentrations are more than 0.9 in all the cases. As the tree density increased, nondimensionalized concentration increased (decreased) near the wall of the upwind (downwind) building, which resulted from the decrease in wind speed case by the drag effect of trees. However, the CFD model underestimated (overestimated) the concentration near the wall of upwind (downwind) building.
Keywords:
CFD model, wind-tunnel experiment, tree-drag effects, flow and dispersion characteristics, street canyon1. 서 론
도시 지역 사람들이 보다 쾌적한 삶을 추구함에 따라 도시 지역 녹화 사업에 대한 관심과 요구가 증가하고 있다. 2000년대에 들어서면서 일정 규모 이상의 도시개발사업 시 공원녹지 확보가 의무화됨(국토해양부령 제 378호)에 따라 도시 내의 공원과 녹지(수목)가 꾸준히 증가하고 있다. 수목은 광화학 작용을 통해 대기 중 이산화탄소를 흡수하고 잎의 증산작용을 통해 기온을 낮추고 수분을 제공하는 등의 순기능을 가지고 있다(Kim and Kim, 2002; Gromke et al., 2015). 그 뿐만 아니라 도심 내의 초록색 공원경관은 사람들에게 심미적 효과를 주고, 수목이 방출해 내는 신선한 공기와 피톤치드는 사람들에게 심리적 안정을 준다. 이에 따라 수목 자체의 생리적 연구 뿐만 아니라 대기질 개선과 정화 효과에 대한 다양한 연구가 수행되고 있다(Jo et al., 1995; Nowak and Crane, 2002; Joo and Park, 2004). 그러나 이 연구들은 시간당 오염물질 흡수량 또는 단위면적당 산소/이산화탄소의 방출/흡수량 등에 관한 연구가 대부분이고 도심속 수목에 의한 흐름 변화와 이에 따른 오염물질 확산에 관한 역학적 연구는 거의 이루어지지 않았다(Gromke et al., 2008). 또한 상세 규모의 흐름과 확산을 이해하기 위해 지금까지 수행된 대부분의 연구(Baik and Kim, 1999; Liu and Barth, 2002; Kim and Baik, 2004)는 주로 건물과 같은 비투과성 장애물들만 고려하였고, 수목이나 식물들과 같은 투과성 장애물에 대한 연구는 최근에 들어서야 연구가 진행되고 있다(Gromke et al., 2008; Balczó et al., 2009).
도시 협곡에서의 수목은 건물과 함께 유동장에 영향을 미치는 장애물 역할을 한다(Gross, 1987). 흐름이 건물과 같은 비투과성 장애물을 통과하게 되면 장애물 양쪽 측면과 지붕 모서리 부근에서 흐름이 분리되고, 장애물 풍하측에서 흐름이 다시 만나는 재순환 지역이 형성된다(Hosker, 1984). 투과성 장애물인 수목 주변에서도 수목의 양쪽 측면과 꼭대기에서 분리되고 풍하측에서 다시 만나는 재순환 지역이 형성된다는 측면에서는 투과성 장애물 주변의 흐름과 유사하다. 그러나 투과성 장애물 내부에는 공극이 존재하고 일부 흐름이 장애물을 투과하여 지나게 되어 잎표면 마찰에 의해 풍속이 감소한다(Ruck and Schmitt, 1986). 수목과 같은 투과성 장애물은 주변 흐름에 영향을 주기 때문에, 수목이 밀집되어 있는 도심 공원이나 가로수가 위치한 도시 협곡의 대기 흐름과 오염물질 확산에 미치는 영향을 이해할 필요가 있다.
본 연구에서는 도시 협곡 내의 수목이 흐름과 스칼라 물질 확산에 미치는 영향을 조사하였다. 이를 위하여 Kim and Baik (2010)의 전산유체역학(computational fluid dynamics, CFD) 모델에 수목의 항력(tree drag force)항을 추가하였다. 수목 항력항이 추가된 CFD 모델을 검증하기 위하여 Gromke et al. (2008)의 풍동 실험 결과를 이용하였다.
2. 연구방법
2.1 수치 모형
본 연구에서 사용한 전산 유체 역학(Computational Fluid Dynamics, CFD) 모델은 Kim and Baik (2010)이 사용한 것과 같다. 이 모델은 3차원 비정수, 비회전, 비압축 대기 흐름을 가정한다. 비선형 응력변형율(strain rate)을 고려하기 위해 Yakhot et al. (1992)이 제시한 재규격화군(renormalization group, RNG) 이론에 근거한 k-ε 난류 모형을 이용하였다. Versteeg and Malalasekera (1995)가 제안한 벽면 함수를 사용하여 벽 근처에서의 점성 효과를 고려하였다.
2.2 수목 효과의 수치 모델링
수목 효과를 수치 모델링을 하기 위해 투과성 장애물을 통과할 때 나타나는 압력 손실을 이용한다(Gromke et al., 2008). 유체 흐름이 수목을 지나게 되면 압력손실이 일어나 풍속이 감소하고, 난류 운동 에너지와 그 소멸률(ε)이 변한다(Balczó et al., 2009). 이러한 풍속 감소 효과는 수목이 존재하는 지역의 지배방정식에 항력항을 부과함으로써 고려할 수 있다. Ries and Eichhorn (2001)은 단위 부피당 수목에 의한 항력을 다음과 같이 제시하였다.
| (1) |
여기서 ρ는 공기 밀도, ui는 i번째 평균 속도 성분, |u|는 평균 속도, λ는 압력손실계수(pressure loss coefficient)이다. 압력손실계수(λ)는 수목이 지표를 덮은 정도와 잎 표면의 거칠기, 단위 부피당 잎의 밀도에 대한 함수로 식(2)와 같이 표현된다.
| (2) |
여기서 cd0는 잎의 항력 계수로 잎 표면의 거칠기와 면적에 따라 0.2에서 2 사이의 값을 가지며, 잎의 표면(표면적)이 거칠수록(넓을수록) 값이 커지게 된다(Gross, 1993). 본 연구에서는 Balczó et al. (2009)과 같이 0.2로 설정하였다. nc는 수목이 지표를 덮은 정도를 나타낸 것으로 수목이 있는 격자는 1이고 없는 격자는 0으로 설정하였다. b는 단위 부피당 잎의 면적으로 정의되는 잎면적밀도(leaf area density, LAD)이고 다음과 같이 표현된다.
| (3) |
여기서 Aleaves는 나뭇잎의 한쪽 면의 면적이고, Vcell는 격자 부피이다. 풍동 실험을 통해 측정한 밀도에 따른 잎면적밀도는 Table 1과 같다. 식(1)~(3)을 이용하여 운동량 방정식, 난류 운동에너지(k)와 소멸률(ε) 방정식에 수목 항력항을 추가하면, 기존의 지배방정식은 다음과 같이 표현된다(Balczó et al., 2009).
| (4) |
| (5) |
| (6) |
여기서, 아래첨자 old는 기존의 지배방정식을 나타내고, 아래첨자 veg는 수목 항력이 포함된 지배방정식을 나타낸다.
2.3 실험 설계
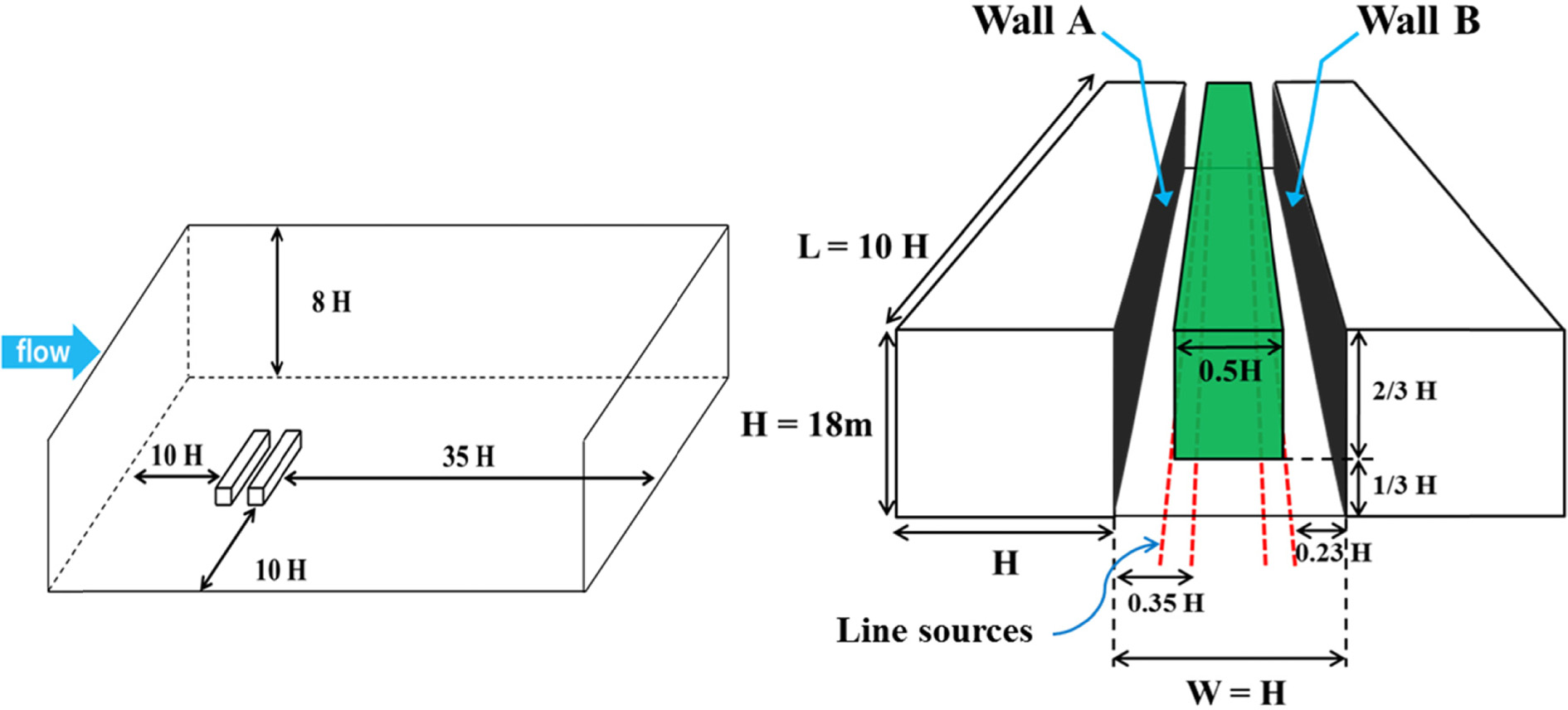
Gromke et al. (2008)의 풍동 실험 결과를 이용하여 수목 항력항을 포함한 CFD 모델을 검증하였고, 수목이 도시 협곡 흐름과 스칼라물질 확산에 미치는 영향을 조사하였다. Figure 1은 수치 도면을 고려한 도시 협곡을 나타낸다. 건물 높이(H)와 건물 사이의 너비(W)는 18 m이고, 건물 길이(L)와 높이의 비(L/H)는 10이다. 건물로부터 풍상측 경계까지 거리를 10H, 측면 경계까지 거리를 10H, 풍하측 경계까지 거리를 35H, 그리고 상층 경계까지 거리를 8H가 되도록 설정하였다. x, y, z 방향의 격자 개수는 각각 500, 120, 100개이고, 격자 크기가 1.5 m, 4.5 m, 1.5 m로 일정한 등격자계를 사용하였다. 시간 간격을 0.5초로 하여 7,200초까지 수치 적분하였다. 수목은 도시 협곡 중심에 위치하고 수목 너비와 높이는 각각 0.5H와 0.67H이다(Fig. 2). 도시 협곡 내에 수목이 없는 경우와 수목의 잎면적밀도가 1.33과 3.33인 경우에 대해서 실험하였다. 대기오염물질은 양쪽 건물로부터 0.23H와 0.35H 떨어진 지표면에서 4개의 선을 따라 초당 10 g씩 7,200초 동안 배출된다. 바람, 난류 운동에너지 소멸률에 대한 유입 경계 조건은 Gromke et al. (2008)에서 사용된 연직 분포를 사용하였고 다음과 같다.
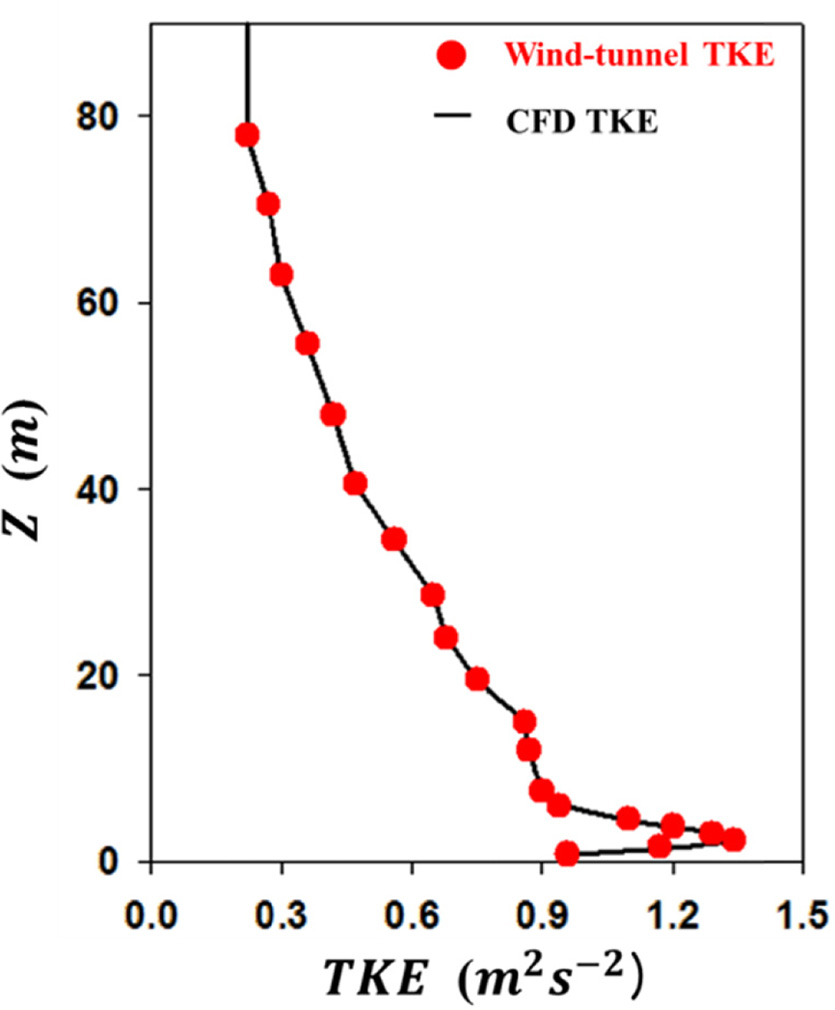
Vertical profile for turbulent kinetic energy (TKE) used as an inflow boundary condition in the CFD model.
| (7) |
| (8) |
여기서 u* (= 0.52 ms−1), κ (= 0.4), δ (= 75 m)는 각각 마찰 속도, von Karman 상수, 경계층 두께이다. 유입 경계에서 y, z 방향의 속도 성분은 0이다. 거칠기길이, z0는 0.0033 m이다. 난류 운동 에너지의 유입 경계 조건은 풍동 실험 결과값을 1차 선형내삽하여 사용하였다(Fig. 2).
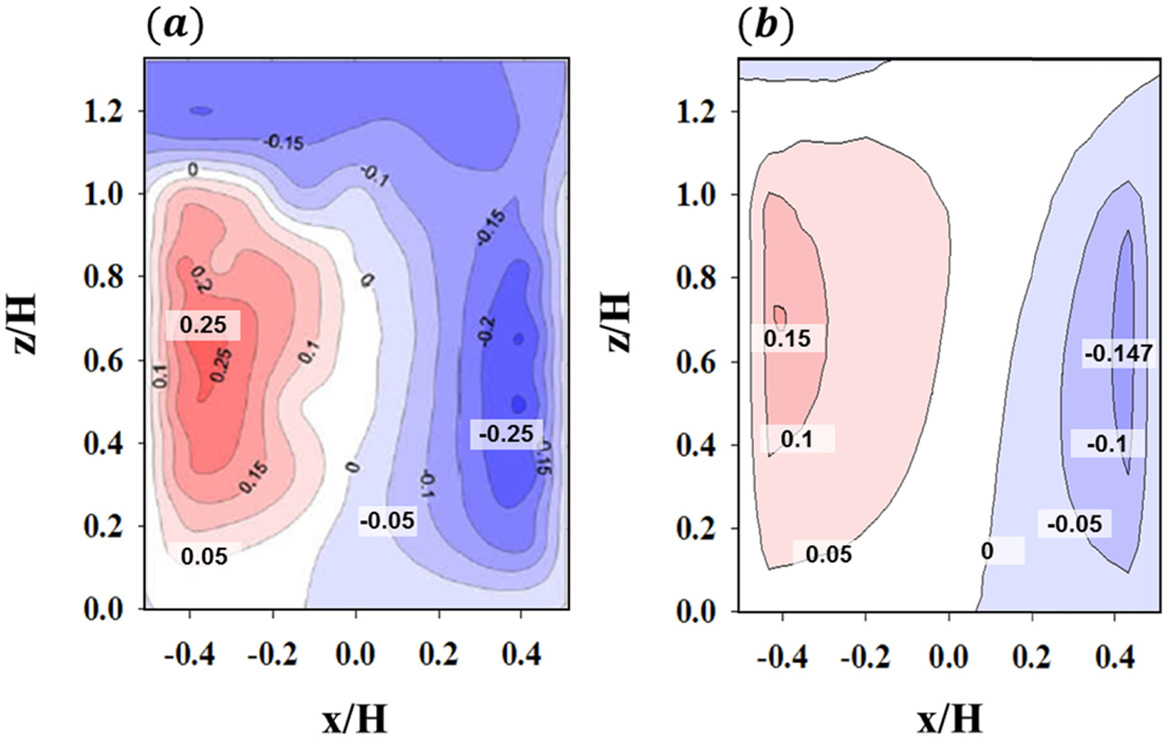
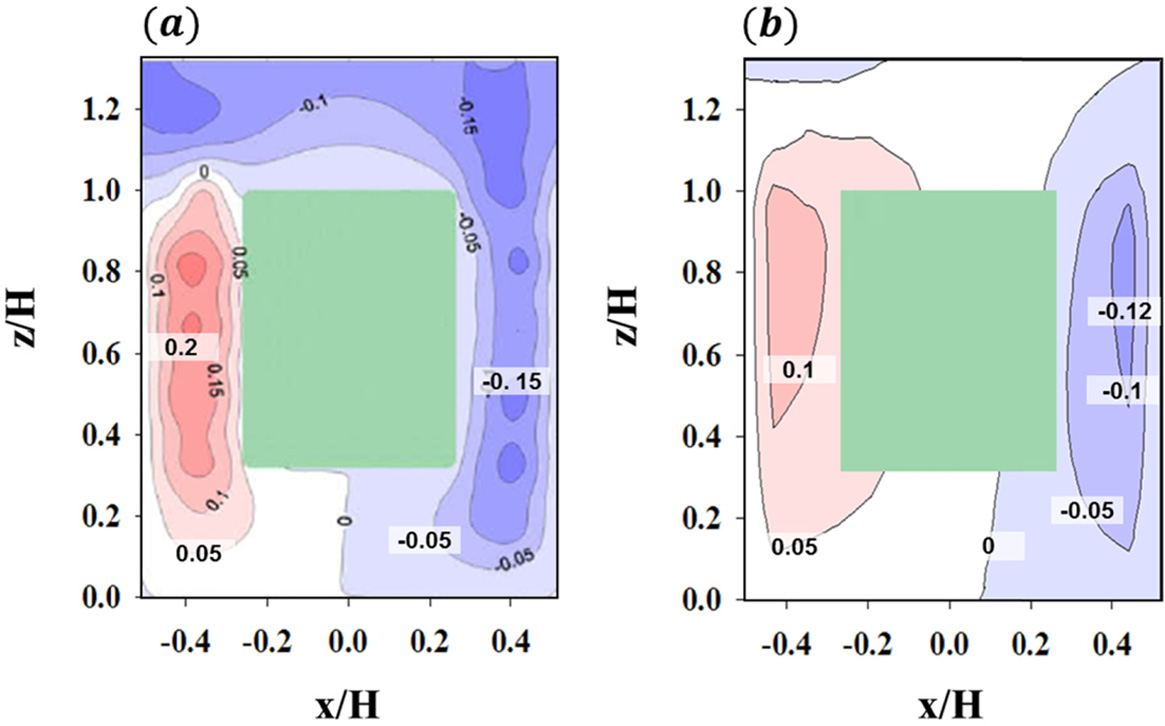
Contours of vertical wind component normalized by the inflow wind speed at z = H for the tree-free case in the (a) wind-tunnel experiment (Gromke et al., 2008) and (b) this study.
3. 결과와 토의
3.1 유동장 특성
수목의 항력 효과를 포함한 CFD 모델을 검증하기 위하여 Gromke et al. (2008)의 풍동 실험 결과와 비교하였다. 먼저, 본 연구에서 사용한 CFD 모델의 도시 협곡 흐름 재현 능력을 조사하기 위하여 수목이 없는 경우에 대한 수치 실험을 선행하였다. Figure 3은 수목이 없는 경우, 도시 협곡 중심(y/H = 0.5)에서 조사한 무차원된 연직 속도 분포를 나타낸다. 풍동 실험 결과를 보면, 소용돌이가 도시 협곡 내부에 갇힌 skimming flow 형태인 것을 확인할 수 있다. 풍상측(−0.5 ≤ x/H ≤ 0)에서는 상승류가, 풍하측(0 ≤ x/H ≤ 0.5)에서는 하강류가 지배적으로 나타나는 것을 확인할 수 있다. 상승류 강도는 건물벽의 마찰로 인해, 벽의 앞 부근(−0.4 ≤ x/H ≤ −0.3)에서 높게 나타난다. 하강류의 경우에는, 지붕 높이의 강한 수평바람이 유입되면서 풍하측 건물 벽면을 따라서 지표면까지(0.2 ≤ z/H ≤ 1)강하게 나타나는 것을 확인할 수 있다. 수치 실험 결과를 보면, 무차원화된 연직 성분 속도의 최대 상승류(하강류)가 풍동 실험 결과의 약 80% (60%)로 약하게 수치 모의하였으나, 풍하측에서 비교적 강한 하강류가 벽면을 따라 지표까지 하강하고, 풍상측에서 다시 상승하는 패턴을 비교적 잘 모의한 것을 확인할 수 있다.
다음은 도시 협곡 중심에 수목이 있는 경우이다. 수목은 지표로부터 1/3H 고도로부터 건물 높이까지 위치한다. 풍동 실험과 비교를 위하여 수목의 밀도가 높은 경우(λ = 250 Pa · m−1)를 고려하였다. 수목이 없는 경우(Fig. 3)와 비교하였을 때, 수목으로 인해 도시 협곡 내의 전체적인 풍속이 감소한 것을 확인할 수 있다(Fig. 4). 또한 상승류와 하강류의 강도가 수목과 건물 사이(−0.5 ≤ x/H ≤ −0.3, 0.3 ≤ x/H ≤ 0.5)에서 비교적 강하고 수목 내부에서는 약한 것을 확인할 수 있다. 본 연구에서 사용한 CFD 모델도 수목의 효과를 잘 반영하여 흐름을 재현한 것을 확인할 수 있다. 앞에서도 언급한 바와 같이, 풍동 실험에 비해 바람을 약하게 수치 모의하였으나, 연직 성분 바람 분포 패턴과 수목에 의한 풍속 감소 현상을 잘 재현한 것으로 판단된다. 최대 하강류의 경우, 풍동 실험에서는 수목에 의해 약 60%까지 감소한 반면 수치 실험에서는 약 81%까지 감소하였다. 최대 상승류의 경우, 풍동실험에서는 수목에 의해 약 80%까지 감소하였고 수치 실험에서는 약 67%까지 감소하였다.
3.2 스칼라 물질 확산 특성
수목이 스칼라 물질의 확산에 미치는 영향을 조사하기 위해 Gromke et al. (2008)의 풍동 실험 결과와 비교하였다. 이를 위해 도시 협곡 내의 수목 밀도가 낮은 경우(λ = 80 Pa · m−1)와 보통인 경우(λ = 200 Pa · m−1)를 고려하였다. CODASC (concentration data of street canyon, http://www.codasc.de)는 풍상측 건물 벽면(A in Fig. 1)과 풍하측 건물 벽면(B)의 오염물질 농도를 무차원하여 제공하고 있다. CODASC는 다음과 같이 정의된 무차원 농도(C+)를 사용한다(Gromke et al., 2008).
| (9) |
여기서 C는 측정된 농도, H는 건물 높이, UH는 건물 높이에서의 풍속, Ql은 단위 길이 당 배출률을 나타낸다.
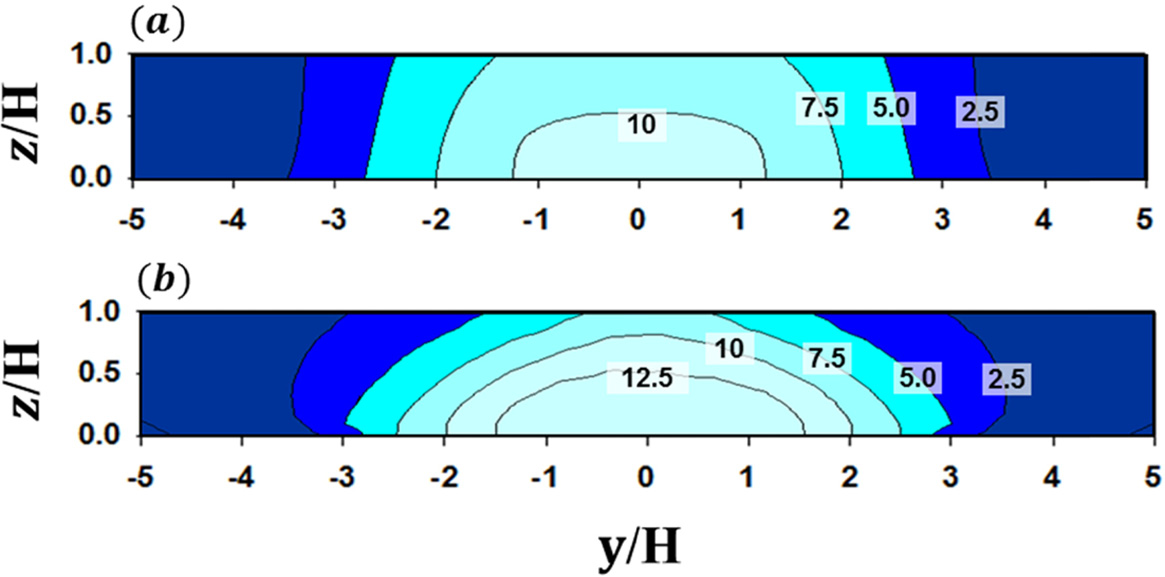
Figure 5는 풍상측 건물 벽면(A)의 무차원화된 농도장을 나타낸다. 풍동 실험의 경우, A면의 중심부의 넓은 지역에 걸쳐서 스칼라 물질 농도가 높게 나타났고, 오염원이 위치하는 도시 협곡 바닥 근처로 갈수록 높은 농도가 나타났다(Fig. 5a). 이는 도시 협곡의 양쪽 측면(y/H = −0.5 and 0.5)에서 협곡 내부로 유입되는 흐름에 의해 도로에서 배출되는 스칼라 물질이 중심부에서 축적되고, 도시 협곡 하층의 역류(reverse flow)에 의해 이류되는 스칼라 물질이 A면을 따라 상승하기 때문이다. 수치 실험의 경우도 풍동 실험 결과와 매우 유사한 분포 패턴이 나타났다. 고농도가 나타나는 영역이 풍동 실험에 비해 비교적 좁고 다소 뾰족한 형태로 분포하는 것을 제외하고는 풍동 실험 결과를 잘 재현함을 확인할 수 있다(Fig. 5b). B면의 경우, A면의 농도에 비해 낮은(최고 농도의 1/4) 농도가 분포하였다(Fig. 6). 이는 도시 협곡의 지붕과 양쪽 측면에서 유입되는 비교적 낮은 농도를 갖는 대기 흐름이 B면에서 수렴되기 때문이다. 풍동 실험에 비해 수치 실험이 스칼라 물질 농도를 다소 과대 모의하고 있지만, 전반적으로 풍동 실험 결과를 잘 재현함을 확인 할 수 있다. 앞에서 살펴본 바와 같이, 본 연구에서 사용한 CFD 모델이 수목이 없는 경우에 풍동 실험의 스칼라 물질 확산 패턴을 정성적으로 잘 모의함을 알 수 있다. 다음은 수목의 항력항을 고려한 CFD 모델 결과를 풍동 실험 결과와 비교하였다. Figure 7은 도시 협곡 내에 수목 밀도에 따른 무차원된 농도장을 나타낸다. 풍동 실험의 경우, 수목 밀도가 증가할수록 (λ가 증가할수록) A면의 농도가 증가하고 B면의 농도는 감소하였다(Figs. 7a~d). 이는 수목으로 인해 도시 협곡 내부의 소용돌이 강도가 감소하면서 스칼라 물질 확산이 잘 일어나지 않고(Figs. 3 and 4), 수목이 일정 부피를 차지함에 따라 도시 협곡 내부의 공기부피가 감소하면서 스칼라 물질 농도가 증가하는 것으로 판단된다. 반면에, B면의 경우에는 소용돌이에 의해 풍상측으로부터 풍하측으로 확산되는 스칼라 물질을 수목이 차단하면서 농도가 감소하였다. 수치 실험 결과를 보면, 수목 밀도가 증가하면서 A면의 농도가 증가하고 B면의 농도는 전반적으로 감소하는 등 풍동 실험의 농도 변화 경향을 잘 재현하는 것을 확인할 수 있다(Figs. 7e~h). 그러나, 수치 모델은 고농도가 나타나는 영역과 무차원화된 농도를 풍동 실험에 비해 과소 모의하였다. 이에 대한 원인을 조사하기 위하여 도시 협곡 중심(y/H = 0)의 농도 분포를 살펴보았다(Fig. 8). 풍동 실험에서는 수목이 물리적인 공간을 차지하지만, 수치 모델에서는 수목이 위치하는 지점에서 수목의 항력만을 고려하기 때문에 풍속 감소 효과만 반영된다. 따라서, 수목이 위치하는 지점에서 고농도의 스칼라 물질이 존재하게 되고, 풍동 실험 결과에 비해 A면의 농도가 과소 모의된 것으로 판단된다. 많은 선행 연구들은 수목의 긍정적인 효과에 대해서 초점을 맞추어서 수행되어 왔다. 그러나, 본 연구 결과에 따르면, 수목은 압력 저하를 일으켜 풍속을 감소시켰다. 이러한 도시 협곡에서 풍속 감소는 자동차 등으로부터 배출된 대기오염물질의 바람에 의한 수송을 약화시킴으로써 대기오염물질 확산에 부정적인 영향을 미침을 알 수 있다.
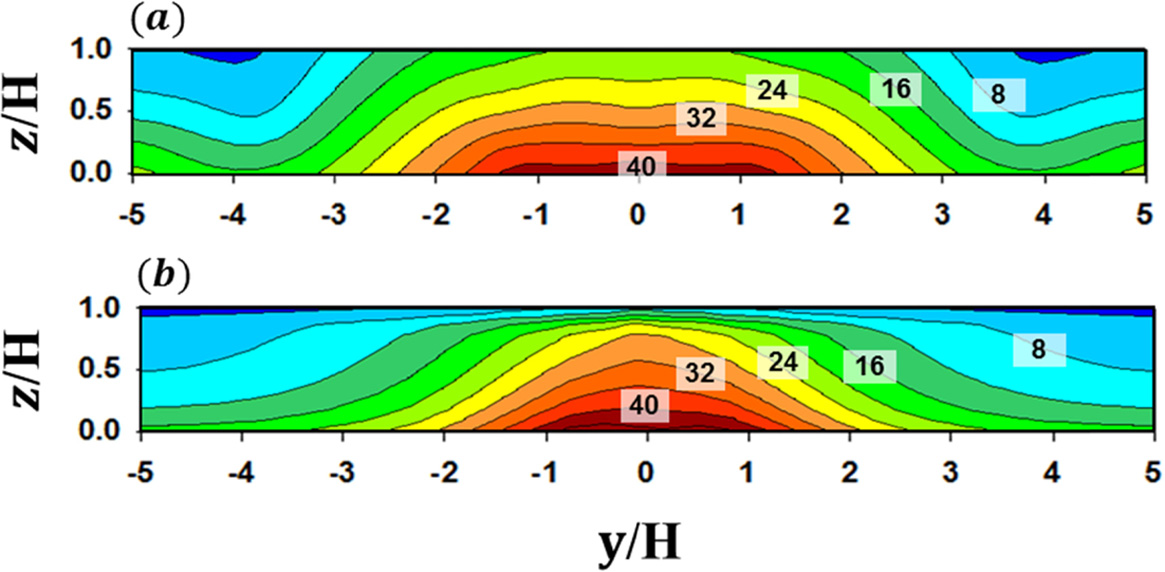
Contours of nondimensionalized concentration (C+) on the wall A for the tree-free case in the (a) wind-tunnel experiment (Gromke et al., 2008) and (b) this study.
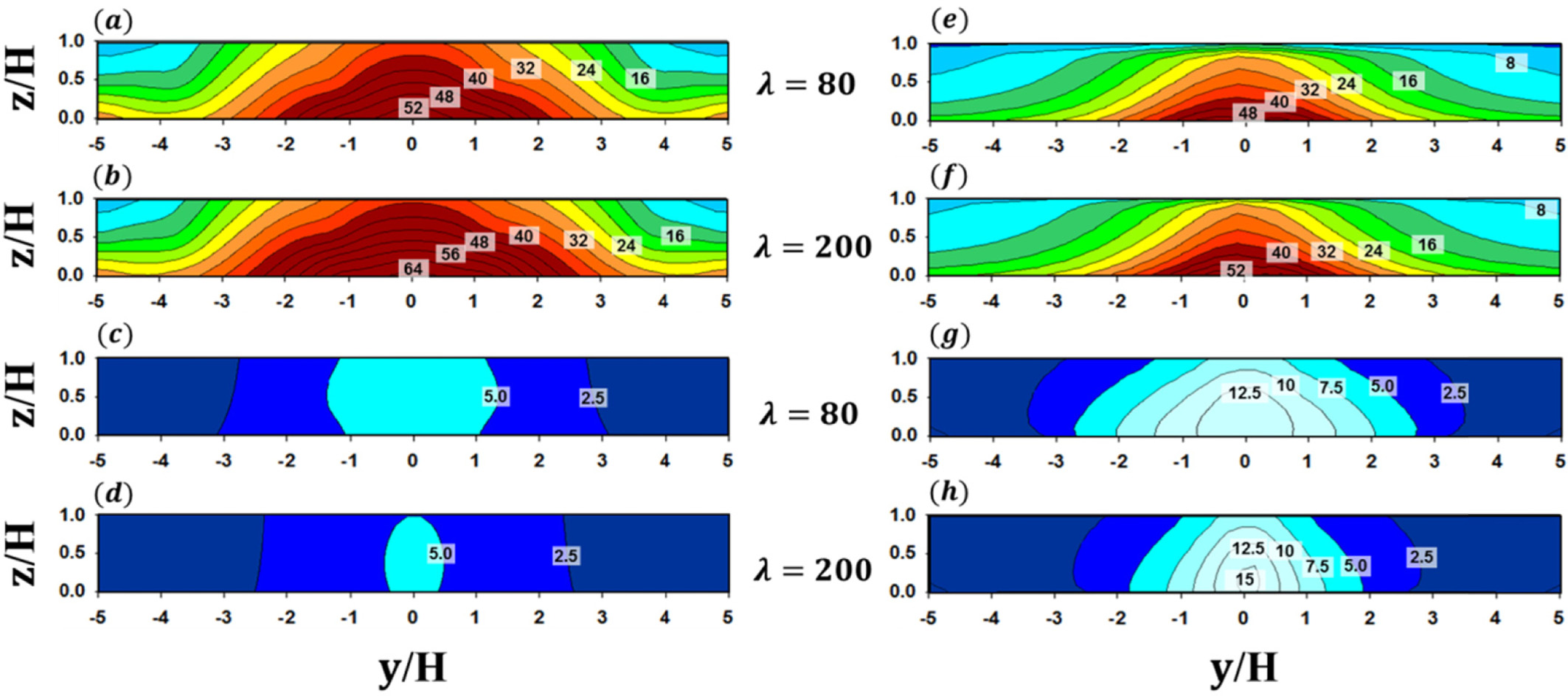
Contours of nondimensionalized concentration (C+) on the A and B walls for the low-density tree [(a), (c), (e), and (g)] and medium-density tree cases [(b), (d), (f), and (h)] in the wind-tunnel experiment by Gromke et al. (2008) (left panel) and this study (right panel).
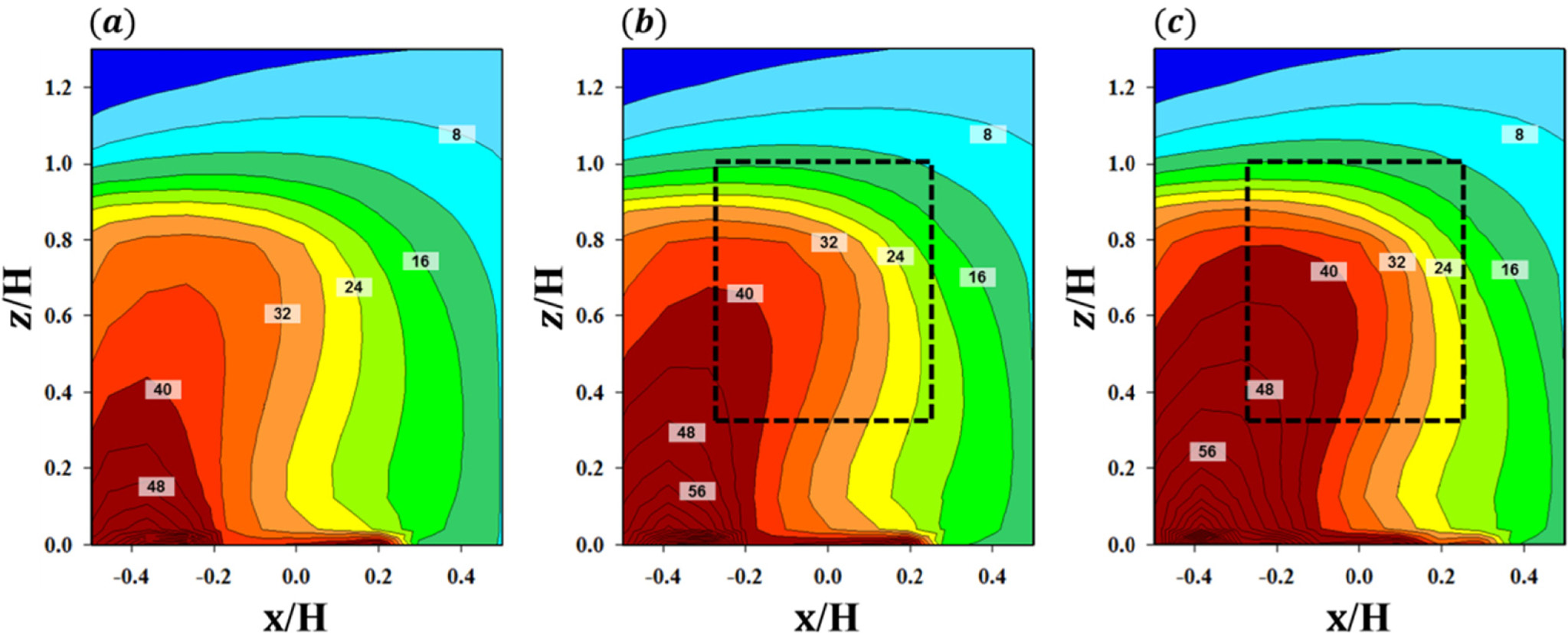
Contours of nondimensionalized concentration (C+) at y/H = 0.5 for the (a) tree-free, (b) low-density tree, and (c) medium-density tree cases in this study.
수치 실험 결과를 정량적으로 검증하기 위하여 Chang and Hanna (2004)가 제안한 방법을 이용하였다. Chang and Hanna (2004)는 관측값과 예측값 사이의 상관성 분석을 위해 정규화된 평균오차제곱(normalized mean square error, NMSE), 편차분율(fractional bias, FB), 2인수범위 내 일치도(the fraction of predictions within a factor of two of observations, FAC2), 기하평균편차(geometric mean bias, MG), 기하평균분산(geometric mean variance, VG), 상관계수(Correlation Coefficient, R) 등을 제시한 바 있다. Chang and Hanna (2004)에 따르면, 관측값을 완벽하게 예측하였을 때, FAC2, MG, VG, R이 1이고 NMSE와 FB가 0이다. Di Sabatino et al. (2011)은 모델 예측 결과가 신뢰성을 확보하기 위해서 가져야 할 권장 범위를 아래와 같이 제시하였다.
NMSE < 4
−0.3 < FB < 0.3
FAC2 ≥ 0.5
MG < 1
VG < 1.5
R > 0.8
Table 2는 풍동 실험 측정 결과와 수치 모델 예측결과를 이용하여 Chang and Hanna (2004)의 통계적 측도를 계산한 결과이다. NMSE, FAC2, R 등은 Di Sabatino et al. (2011)의 권장 범위를 잘 만족하는 것을 확인할 수 있다. 반면, VG와 MG는 수목이 있는 경우에, 각각 한쪽 벽면(VG는 B벽면, MG는 A벽면)에 대해서만 권장 범위를 만족하였다. 이는 스칼라 물질 농도를 A벽면에서는 과소 모의하고, B벽면에서는 과대 모의하여 나타난 결과로 판단된다. 또한 FB 경우에는 수목이 있는 경우에, 권장 범위를 만족하지 못하는 것을 확인할 수 있다. 전반적으로 본 연구에서 사용한 CFD 모델은 정량적인 측면에서 일부 통계적 측도를 만족시키지 못했지만, 풍동 실험 결과를 정성적으로는 잘 재현하였다. 이는, 앞에서 언급한 바와 같이, 수목이 차지하는 물리적인 공간을 수치 모델에서는 제대로 반영하지 못해서 나타난 결과라고 판단된다. 향후, 보다 현실적인 수목 효과를 수치 모의하기 위해서는 이에 대한 보완이 필요할 것으로 판단된다.
4. 요약과 결론
본 연구는 도시 협곡에서 수목으로 인한 흐름 변화와 스칼라 물질 확산에 대하여 연구하였다. 이를 위하여 CFD 모델에 수목의 항력 효과를 반영하였고 풍동 실험 결과와 비교 · 분석하였다. 외관비가 1인 도시 협곡 중심부에 수목을 위치시켰고, 수목 유무에 따른 흐름장 변화를 분석하기 위하여 수목이 없는 경우와 수목의 잎면적밀도가 높은 경우에 대해서 수치 실험을 수행하였다. 또한 스칼라 물질의 확산 분석을 위하여 잎면적밀도가 낮은 경우와 보통인 경우에 대해서 수치 실험을 수행하였다.
수목 유무에 따라 도시 협곡에 형성되는 흐름 패턴은 수치 실험이 풍동 실험을 전반적으로 잘 모의하였으나, 풍속을 다소 과소 모의하였다. 수목이 있는 경우에 수목의 항력으로 풍속이 크게 감소하였고, 풍상측(풍하측)에서 상승(하강)하는 흐름이 다소 감소하였는데, 이는 풍동 실험 결과와 정성적으로 잘 일치한 것이다. 도시 협곡 지표면을 따라 스칼라 물질이 배출되도록 설계하여 수목의 잎면적밀도에 따른 스칼라 물질의 확산 분포를 풍동 실험과 비교 · 분석하였다. 수목의 잎면적밀도가 증가하면서 풍상측 벽면의 농도는 증가하고 풍하측 벽면 농도는 감소하였는데, 이 결과는 풍동 실험 결과와 잘 일치한다. 수치 모델은 풍상측(풍하측) 벽면의 농도를 과소(과대) 모의하였지만, 전반적으로 풍동 실험 결과에서 나타난 스칼라 물질의 농도 분포 패턴을 정성적으로 잘 재현하였다. 통계적 측도를 이용하여 수치 모델의 모의 결과를 풍동실험 결과와 정량적으로 검증하였다. 정규화된 평균 오차제곱, 2인수범위 내 일치도, 상관계수 등은 선행연구에서 제안한 허용 범위를 매우 잘 만족시켰다. 수치 모델이 수목의 물리적인 부피를 고려하지 못함으로써 풍상측 벽면 농도를 과소 모의하고 풍하측 벽면 농도를 과대 모의 했다. 이로 인해 편차분율, 기하평균편차, 기하평균분산 등의 측도를 일부 만족시키지 못했다. 향후, 보다 현실적인 수목 효과를 수치 모의하기 위해서는 이에 대한 보완이 필요할 것으로 판단된다.
도시 지역 흐름과 확산에 관한 연구의 대부분은 건물과 같은 비투과성 장애물만 고려하여 수행되어왔다. 도심지 수목과 녹지공원이 증가하고 있기 때문에, 보다 현실적인 수치 모의를 위해서는 수목과 녹지의 효과를 반영해야 할 것으로 판단된다. 향후, 본 연구에서 사용한 CFD 모델을 개선하고 실제 도시 지역에 적용하여 수목이 흐름과 확산에 미치는 영향에 관한 연구를 수행하고자 한다.
Acknowledgments
이 연구는 부경대학교 자율창의학술연구비(2015년)에 의하여 연구되었습니다. 논문에 대해 유익한 지적을 해주신 심사위원님께 감사드립니다.
References
-
Baik, J.-J., and J.-J. Kim, (1999), A numerical study of flow and pollutant dispersion characteristics in urban street canyons, J. Appl. Meteorol, 38, p1576-1589.
[https://doi.org/10.1175/1520-0450(1999)038<1576:ANSOFA>2.0.CO;2]

-
Balczó, M., C. Gromke, and B. Ruck, (2009), Numerical modeling of flow and pollutant dispersion in street canyons with tree planting, Meteorol. Z.,, 18, p197-206.
[https://doi.org/10.1127/0941-2948/2009/0361]

-
Chang, J. C., and S. R. Hanna, (2004), Air quality model performance evaluation, Meteorol. Atmos. Phys, 87, p167-196.
[https://doi.org/10.1007/s00703-003-0070-7]

-
Gromke, C., R. Buccolieri, S. Di Sabatino, and B. Ruck, (2008), Dispersion study in a street canyon with tree planting by means of wind tunnel and numerical investigations-evaluation of CFD data with experimental data, Atmos. Environ, 42, p8640-8650.
[https://doi.org/10.1016/j.atmosenv.2008.08.019]

-
Gromke, C., B. Blocken, W. Janssen, B. Merema, T. van Hooff, and H. Timmermans, (2015), CFD analysis of transpirational cooling by vegetation: Case study for specific meteorological conditions during a heat wave in Arnhem, Netherlands, Build. Environ, 83, p11-26.
[https://doi.org/10.1016/j.buildenv.2014.04.022]

-
Gross, G., (1987), A numerical study of the air flow within and around a single tree, Bound-lay. Meteorol, 40, p311-327.
[https://doi.org/10.1007/BF00116099]

-
Gross, G., (1993), Numerical simulation of canopy flow, Springer, p167.
[https://doi.org/10.1007/978-3-642-75676-4]

- Hosker, R. P., (1984), Flow and diffusion near obstacles, Atmos. Sci. Power. Prod, 3, p241-326.
- Jo, H.-K., Y.-H. Yun, and K.-E. Lee, (1995), Atmospheric CO2 Sequestration by Urban Greenspace-In the Case of Chuncheon, J. Korean. Inst. Tradit. Landsc. Archit, 23, p80-93.
- Joo, O.-J., and Y.-K. Park, (2004), A Study on the Environment- friendly Evaluating Strategies of Green Space in a Housing Complex - Focused on the Amount of O2 Production and Atmospheric Purification of the trees, J. Archit. Inst. Korea, 20, p67-74.
- Kim, S.-B., and H.-D. Kim, (2002), Influences of urban tree on the control of the temperature, J. Korean Inst. Tradit. Landsc. Archit, 30, p25-34.
-
Kim, J.-J., and J.-J. Baik, (2004), A numerical study of the effects of ambient wind direction on flow and dispersion in urban street canyons using the RNG k-ε turbulence model, Atmos. Environ, 38, p3039-3048.
[https://doi.org/10.1016/j.atmosenv.2004.02.047]

-
Kim, J.-J., and J.-J. Baik, (2010), Effects of street-bottom and building-roof heating on flow in three-dimensional street canyons, Adv. Atmos. Sci, 27, p513-527.
[https://doi.org/10.1007/s00376-009-9095-2]

-
Liu, C. H., and M. C. Barth, (2002), Large-eddy simulation of flow and scalar transport in a modeled street canyon, J. Appl. Meteorol, 41, p660-673.
[https://doi.org/10.1175/1520-0450(2002)041<0660:LESOFA>2.0.CO;2]

-
Nowak, D. J., and D. E. Crane, (2002), Carbon storage and sequestration by urban trees in the USA, Environ. Pollut, 116, p381-389.
[https://doi.org/10.1016/S0269-7491(01)00214-7]

-
Ries, K., and J. Eichhorn, (2001), Simulation of effects of vegetation on the dispersion of pollutants in street canyons, Meteorol. Z, 10, p229-233.
[https://doi.org/10.1127/0941-2948/2001/0010-0229]

-
Ruck, B., and F. Schmitt, (1986), Das strömungsfeld der einzelbaumumströmung, Forstwissenschaftliches Centralblatt, 105, p178-196.
[https://doi.org/10.1007/BF02741710]

-
Sabatino, S. D., R. Buccolieri, H. R. Olesen, M. Ketzel, R. Berkowicz, J. Franke, and A. Starchenko, (2011), COST 732 in practice: the MUST model evaluation exercise, Int. J. Environ. Pollut, 44, p403-418.
[https://doi.org/10.1504/IJEP.2011.038442]

- Versteeg, H. K., and W. Malalasekera, (1995), An Introduction to Computational Fluid Dynamics: The Finite Volume Method, Longman, p257.
-
Yakhot, V., S. A. Orszag, S. Thangam, T. B. Gatski, and C. G. Speziale, (1992), Development of turbulence models for shear flow by a double expansion technique, Phys. Fluids, A4, p1510-1520.
[https://doi.org/10.1063/1.858424]