FT-IR을 이용한 중요 광물의 적외 방출도 스펙트럼 측정
Abstract
This study measured the emissivity spectra of 5 major rock-forming minerals using a Fourier Transform Infrared (FT-IR) spectrometer in the spectral region of 650~1400 cm−1. The mineral samples are quartz, albite, bytownite, anorthite, and sandstone. We compared emissivity spectra measured in this study with spectra provided by Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) and Arizona State University (ASU). The spectral features of emissivity such as Reststrahlen Band (RB) and Christiansen Feature (CF) locations were compared. Results showed that both CF and RB locations of emissivity spectra measured in this study were similar to those from ASTER and ASU. In the case of quartz, the RB was occurred in the region of 700~850 cm−1 and 1050~1250 cm−1. The spectral position of emissivity peak was in good agreement with the location of ASTER and ASU. For plagioclase (albite, bytownite, and anorthite), the spectral location of CF was shifted toward larger wavenumber and the emissivity value was increased in the region of 870~1200 cm−1 with Ca percentage. The CF of anorthite and bytownite was occurred at 1245.79 cm−1, and that of albite was occurred at 1283.79 cm−1. We also confirmed that emissivity feature of sandstone includes both emissivity features of quartz and calcite. However, there were some differences in the magnitude of emissivity and locations of RB and CF. These were due to the differences in measurement methods, and differences in particle size and temperature of samples.
Keywords:
FT-IR, infrared spectra, mineral composition, emissivity, laboratory measurement1. 서 론
위성의 적외채널로 측정한 지구-대기계의 복사에너지는 지표로부터 방출되는 에너지와 대기로부터 방출되는 에너지로 구성된다. 특히 대기의 광학두께가 작은 파장의 경우 지표에서 방출된 에너지의 기여가 상당한 부분을 차지하게 된다. 그리고 이러한 파장의 위성자료를 이용하여 지표 온도를 산출할 때에는 지표 방출도의 정보가 산출한 지표 온도의 정확도에 영향을 미치게 된다. Qin and Karnieli (1999)은 NOAA (National Oceanic and Atmospheric Administration)에 탑재된 AVHRR (Advanced Very High Resolution Radiometer)의 채널 5 (10.39~11.0 μm)와 채널 6 (11.50~12.50 μm)을 이용하여 지표 온도(Land Surface Temperature, LST)를 산출할 때 지표의 방출도가 산출한 지표 온도의 정확도에 중요한 영향을 미친다고 지적하였다. 또한 2010년 발사된 천리안 위성 (Communication, Ocean, and Meteorological Satellite, COMS)의 2개 적외채널(10.3~11.3 μm, 11.5~12.5 μm) 자료를 이용한 지표 온도 산출에서도 지표 방출도의 정확성이 요구 된 바 있다(Cho and Suh, 2013). 지표 방출도에 3%의 오차가 있다면 위성 적외채널 자료를 이용하여 산출한 지표 온도는 약 3 K 정도의 오차를 나타내며(Schmugge et al., 1998), 0.5%의 방출도 오차는 산출한 지표 온도에 0.3~0.7 K 오차를 나타낸다(Hulley and Hook, 2009).
적외영역에서 물질의 방출도 스펙트럼은 FT-IR (Fourier Transform Infrared Spectrometer)을 이용하여 물질이 방출하는 복사강도를 측정하거나(Nerry et al., 1990; Christensen and Harrison, 1993; Henderson et al., 1996; Mathew et al., 2009) 반사도를 측정하여(Salisbury et al., 1994; Korb et al., 1999; Chunnilall and Theocharous, 2012) 구할 수 있다. 이러한 방출도 자료는 위성 자료를 이용하여 산출한 지표 방출도를 검증하거나 복사모델을 이용하여 위성이 측정하는 복사강도를 모의하는 데 활용된다.
NASA에서는 JPL (Jet Propulsion Laboratory), JHU (Johns Hopkins University), 그리고 USGS (U.S. Geological Survey) 반사도 자료를 Advanced Spaceborne Thermal Emission and Reflection Radiometer Spectral Liberary(이하 ASTER)로 통합하여 온라인으로 제공하고 있다(Baldridge, 2009). ASTER는 암석, 광물, 토양, 식물, 눈, 얼음과 같은 자연적 물질과 아스팔트와 같은 인공적인 물질의 반사도를 0.4~2.4 μm와 2~25 μm의 파장대로 나누어 제공하고 있다. 또한 ASU 스펙트럼 자료(Arizona State University Spectral Library, 이하 ASU)에서는 150개 이상 광물의 방출도 스펙트럼을 제공하고 있다(Christensen et al., 2000).
본 연구에서는 지표면 물질 중 우리나라의 기반암을 구성하고 있는 주요 광물의 적외영역 방출도를 FTIR 간섭계를 이용하여 측정하였다. 국내에서는 이러한 관측이 처음으로 수행되어 비교할 수 있는 자료가 없었기 때문에 본 연구에서의 측정 자료는 ASTER와 ASU가 제공하는 방출도 스펙트럼과 비교하였다.
2. FT-IR 이론
2.1 FT-IR과 측정 장비
본 연구에서는 광물 시료가 방출하는 빛 에너지를 측정하기 위하여 미국의 Midac Corp.에서 제작된 M4400 FT-IR을 이용하였다. 이 장비는 Michelson 간섭계로서 분할기, 고정거울, 이동거울, 집광기, 검출기 등으로 구성되어 있다. Liquid Nitrogen (LN2)으로 냉각되는 MCT (Mercury Cadmium Telluride) 검출기의 유효 검출범위는 400~5000 cm−1이며, 측정 분해능은 Midac에서 제공되는 소프트웨어를 이용하여 0.5~32 cm−1 범위에서 선택가능하다.
FT-IR로 측정한 자료를 복사강도로 변환하기 위해 사용한 흑체는 Mikon Inc.가 제작한 M340이다. 이 흑체의 설정 가능 온도범위는 −20~150oC이며 온도 분해능은 0.1oC이다. 그리고 광물 시료가 방출하는 에너지를 증가시키기 위하여 시료를 가열하였는데, 가열장치는 0~300oC 범위에서 온도 설정이 가능하며 시료의 온도를 일정하게 유지할 수 있다.
2.2 복사강도 스펙트럼 계산
FT-IR로 측정한 간섭자료(interferogram)를 푸리에 변환하면 파수에 따른 빛 에너지의 분포, 즉 스펙트럼이 된다. 빛 에너지가 장비의 임의 단위(machine unit)로 표시되었을 때, 이를 원시 스펙트럼 Vs(ω)라 한다. FT-IR 간섭계 부품들이 방출한 빛 에너지의 기여(instrument offset)를 제거하고, 시료가 방출한 빛 에너지를 복사강도 스펙트럼(S(ω))으로 나타내기 위해 다음과 같은 정량화 방법(Revercomb et al., 1988)을 사용하였다.
| (1) |
여기서 r(ω)는 FT-IR의 반응도(instrument response function)이며 Io(ω)는 FT-IR 간섭계가 방출한 빛의 기여를 의미한다. FT-IR의 반응도는 검출기에 입사한 빛 에너지와 검출기가 나타내는 수신 에너지 사이의 변환계수(conversion factor)를 의미하며 다음과 같이 정의된다(Mathew et al., 2009).
| (2) |
여기서 Vh(ω)와 Vc(ω)는 각각 온도가 높은 흑체와 온도가 낮은 흑체를 측정한 원시 스펙트럼이다. 그리고 Bh(ω)와 Bc(ω)는 각각 고온과 저온의 흑체가 방출하는 Planck 함수로 다음과 같이 정의된다.
| (3) |
여기서 h (= 6.62617 × 10−33 J s−1)는 Planck 상수이고 k (= 1.38066 × 10−23 J K−1)는 Boltzmann 상수이며 c (= 2.9979 × 108 m s−1)는 진공 상태에서 빛의 속도이다.
그리고 FT-IR 수감부가 입사하는 빛 에너지에 선형으로 반응한다면, 식(1)의 간섭계 기여는 다음과 같이 정의된다(Ishii and Ono, 2001).
| (4) |
식(1)로 계산된 시료의 복사강도 스펙트럼이 본 연구의 방출도 계산에 사용되었다.
2.3 FT-IR의 NESR
방출도 측정에 사용한 M4400 FT-IR 간섭계의 잡음(noise) 크기를 살펴보기 위하여 NESR (Noise Equivalent Spectral Radiance)을 측정하였다. NESR은 흑체를 측정한 원시 스펙트럼의 표준편차와 간섭계 반응도의 비율로 다음과 같이 정의된다.
| (5) |
흑체를 측정하였을 때 원시 스펙트럼의 표준편차 σV(ω)는 다음과 같이 계산하였다.
| (6) |
여기서 Vs(ω)은 원시 스펙트럼 자료이며 는 이들 자료의 평균을 나타낸다.
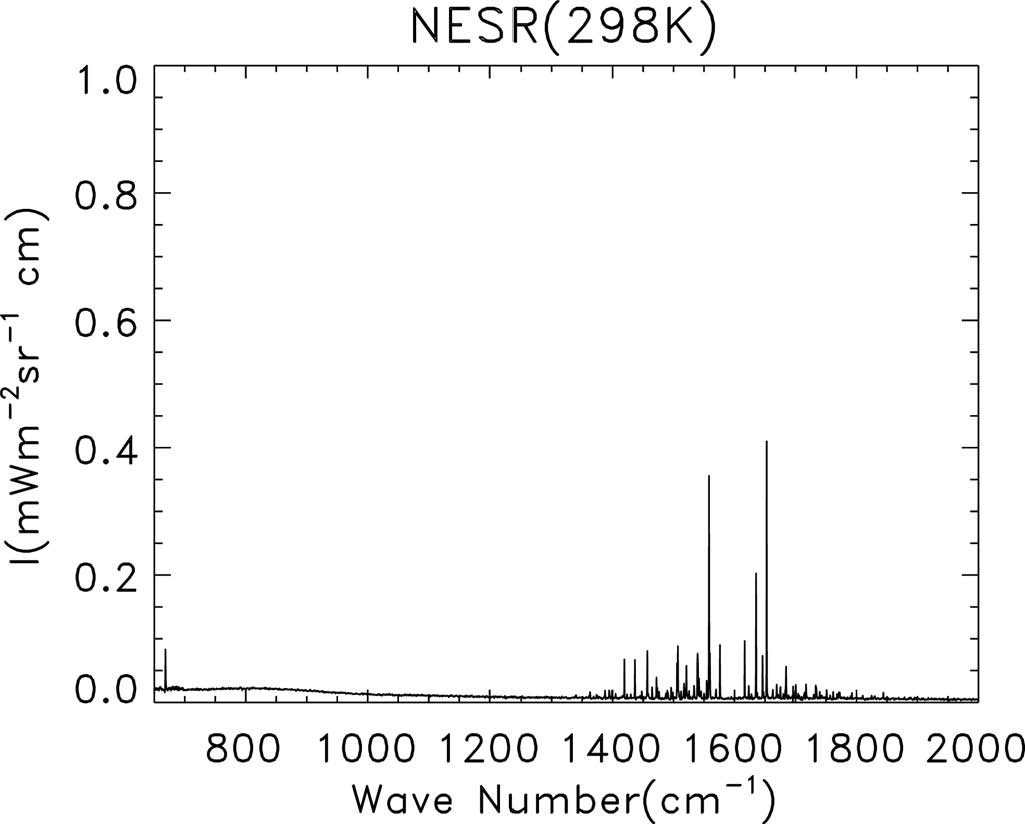
Figure 1은 25oC의 흑체를 20회 측정한 자료를 이용하여 계산한 NESR을 나타낸 것이다. 장비 내부에 존재하는 수증기의 영향으로 파수범위 1400~1700 cm−1 에서 NESR은 강한 수증기 흡수선 위치에 큰 값이 나타났다. 이들을 제외하면 NESR은 10−3~10−2 정도의 작은 값을 나타내었다. 따라서 1400 cm−1보다 작은 파수에서는 NESR이 10−3 이하로 거의 일정하기 때문에수증기의 영향을 받는 범위를 제외한 영역의 자료는 방출도 측정에 사용할 수 있을 것으로 사료된다.
3. 방출도 측정
3.1 방출도
물질의 방출도(emissivity, ε(ω))는 물질이 방출하는 빛 에너지와 그 물질과 동일한 온도의 흑체가 방출하는 빛 에너지의 비율로 정의되며, 물질의 종류와 온도 그리고 파장에 따라 다르다(Norman and Becker, 1995). 방출도의 측정은 반사도(reflectivity, R(ω))를 측정하여 키르히호프 법칙으로 계산하거나 물질의 방출에너지를 측정하여 흑체의 방출에너지와 비교하는 방법이 있다. 이는 각각 식(7)과 식(8)와 같이 정의된다.
| (7) |
| (8) |
여기서 S(ω)는 시료의 방출 복사강도 스펙트럼이고 B(ω)는 시료와 동일한 온도에서 흑체가 방출한 복사강도의 스펙트럼이다.
3.2 광물 시료
광물이란 화학 조성이 일정하고 원자 배열이 규칙적인 결정체이다. 광물은 화학 조성에 따라 분류되며 규산염 광물은 지각의 95% 그리고 지구 상부 맨틀의 97%을 차지한다(Sen, 2001).
우리나라의 기반암은 대리암, 각섬암, 화강질 편마암, 화강암, 사암 등 화강암과 변성암, 그리고 퇴적암으로 이루어져 있다. 이 암석을 구성하는 주요 광물군으로는 석영(quartz), 백운모(muscovite), 사장석(plagioclase), 칼륨장석(K-feldspar) 등이 있다(Hwang et al., 2000). 또한 Jeong (2008)은 봄철 중국으로부터 유입되는 황사의 성분이 규산염 광물인 석영, 사장석, 칼륨장석, 필로규산염(phyllo-silicates) 그리고 탄산염광물(carbonate minerals)인 방해석(calcite) 등으로 구성되어 있음을 보고한 바 있다.
본 연구에서는 지표를 구성하고 있는 주요 광물로 시료를 선정하였다. 시료는 석영(quartz), 사장석 종류인 회장석(anorthite), 아회장석(bytownite), 조장석(albite), 그리고 사암(sandstone)을 포함하여 총 5종이다. 사암은 하나 이상의 광물로 이루어진 암석으로 구성 광물의 방출도 특징을 나타내기 때문에 이를 확인하고자 시료에 포함하였다. 시료들은 평균 가로 9 cm, 세로 6.5 cm, 높이 2.7 cm의 결정체로 경북대학교 지질학과에서 제공되었다.
3.3 시료의 방출 에너지 측정
광물 시료가 방출하는 빛 에너지를 측정하기 위하여 가열장치로 시료를 50~70oC로 가열하였다. 시료를 가열하는 이유는 방출 에너지가 온도에 비례하기 때문에 더 많은 방출 에너지를 측정하여 그 정확도를 높이기 위한 것이다. 그리고 시료의 표면에는 접촉식 온도계를 부착하여 시료의 온도를 측정하였다.
FT-IR을 이용하여 먼저 시료의 간섭자료를 측정하고 차례로 시료보다 온도가 높은 흑체와 시료보다 온도가 낮은 흑체의 간섭자료를 측정하였다. 간섭자료의 측정에서 분해능은 1 cm−1로 하였으며, 자료의 정확도를 높이기 위하여 64번 스캔한 자료의 평균값을 이용하였다. 이들 간섭자료를 푸리어 변환하여 시료의 원시 스펙트럼 Vs와 고온 및 저온 흑체의 원시 스펙트럼 Vh와 Vc를 구하였다. 식(1)을 이용하여 각각의 복사강도 스펙트럼으로 변환한 후, 식(8)을 이용하여 시료의 방출도를 구하였다.
4. 실험 결과
4.1 방출도 스펙트럼
광물의 방출도 스펙트럼에는 Reststrahlen Band(이하 RB)와 Christiansen Feature(이하 CF)가 나타난다(Salisbury and Walter, 1989; Cooper et al., 2002; Donaldson Hanna et al., 2012). RB는 방출도 스펙트럼에서 다른 파장에 비해 값이 작게 나타나는 구간으로 광물 구성 분자들의 진동에 의해 에너지가 흡수되는 파장 영역이다. 석영의 경우 Si-O의 늘임 진동에 의한 흡수대가 8.2~9.2 μm에서 나타난다고 보고된 바 있다(Salisbury and Walter, 1989). Conel (1969)에 의해 처음 사용된 CF는 방출도가 최대가 되는 구간으로 시료의 실수부 굴절율이 시료를 둘러싼 매질의 굴절율에 근접한 파장에 나타나는 것으로 광물을 구분하는 지표로 활용된다(Cooper et al., 2002; Johnson et al., 2002; Bras and Erard, 2003).
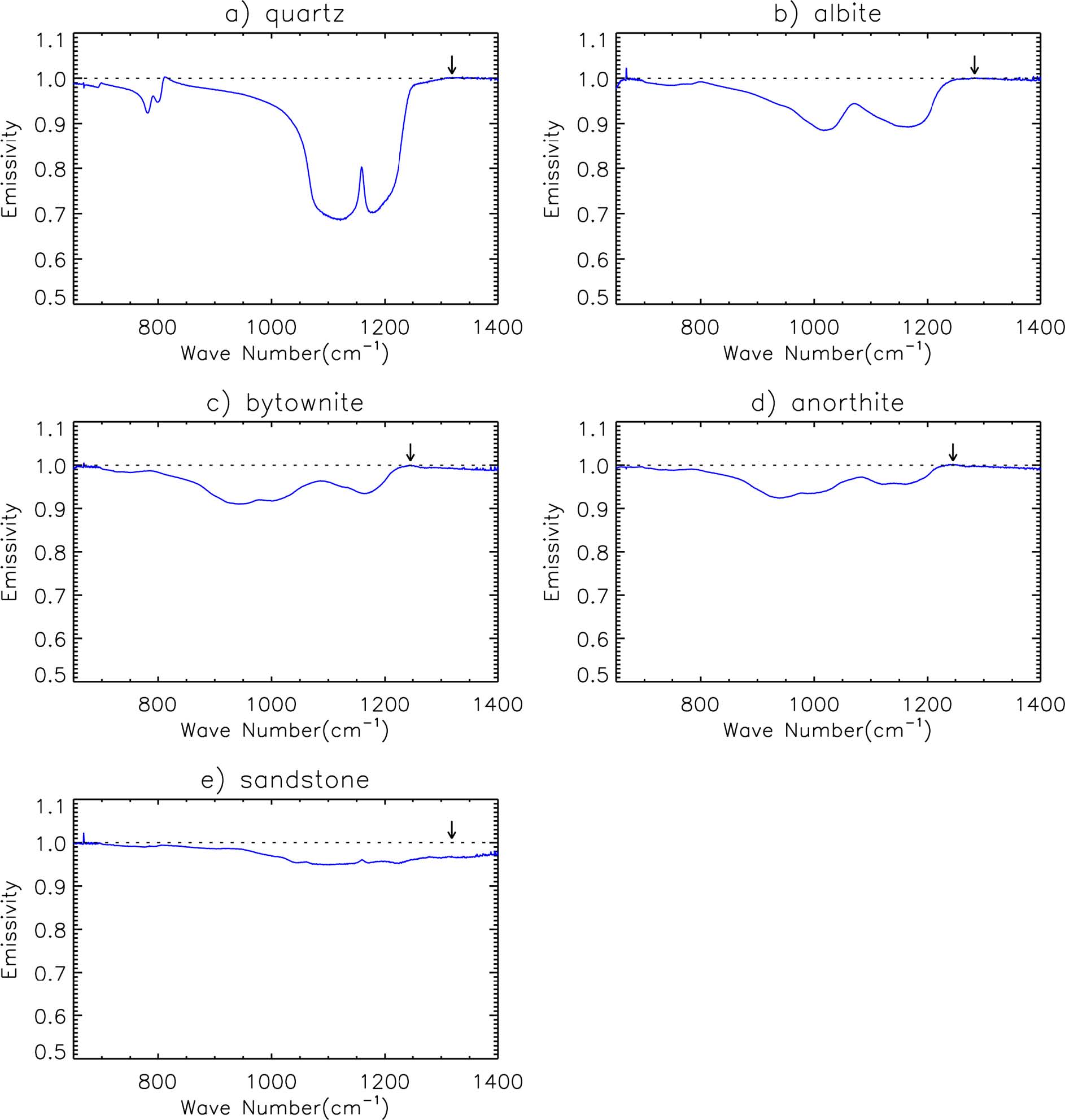
Figure 2는 본 연구에서 측정한 시료들의 방출도를 나타낸 것이다. 스펙트럼 범위는 수증기 흡수대를 제외한 650~1400 cm−1 영역이다. Figure 2a는 온도가 327.15 K인 석영(quartz)의 방출도를, Figs. 2b~d는 조장석(albite, 334.15 K), 아회장석(bytownite, 349.45 K), 회장석(anorthite, 330.85 K)의 방출도를, 그리고 Fig. 2e는 사암(sandstone, 330.35 K)의 방출도를 나타낸 것이다.
Christensen and Harrison (1993)은 석영의 방출도 스펙트럼에서 790 cm−1와 1160 cm−1 부근에 RB가 있으며 이들은 비대칭으로 나타난다고 보고하였다. 본 연구에서 측정한 석영의 경우, RB 구간인 700~850 cm−1에서 평균 방출도는 약 0.944이고 1050~1250 cm−1에서 평균 방출도는 약 0.754였다. 두 RB 구간을 제외한 영역에서의 평균 방출도는 0.976으로 RB에서의 방출도와 0.03~0.22의 차이가 났다. 최소 방출도는 1121.41 cm−1에서 나타났으며 방출도는 0.685이다. 그리고 1178.29 cm−1에서 다른 최소 방출도가 나타났으며 그 크기는 약 0.702이다. 이들은 1158 cm−1을 기준으로 비대칭을 보이는데, 이러한 비대칭은 Salisbury and Walter (1989)와 Wenrich and Christensen (1996)의 연구에서도 보고된 바 있다. 석영의 CF는 온도에 따라 달라질 수 있지만(Salisbury and Walter, 1989), 본 연구에서 측정한 1337.87 cm−1의 CF는 Wenrich and Christensen (1996)의 연구에서 보고한 CF의 위치(1360 cm−1 부근, 298.15 K)와 비슷하였다.
본 연구에서 측정한 조장석, 아회장석, 회장석은 장석(feldspar) 중에서 사장석으로 분류되는 광물들이다. Milam et al. (2004)의 연구에 따르면 사장석의 방출도 스펙트럼 특징은 다음과 같다: (1) 1250~1351 cm−1에서 CF 가 나타나며, (2) 규소(Si)와 알루미늄(Al) 원자들 간의 늘임 진동에 의한 흡수로 900~1100 cm−1와 700~800 cm−1에서 RB가 나타나고, (3) 회장석(Ca)의 포함량이 많을수록 CF가 나타나는 파수는 감소한다. 아울러 약 1050 cm−1에서 방출 에너지가 나타난다는 것이 선행 연구에서 보고된 바 있다(Wagner, 2000; Milam et al., 2004; Donaldson Hanna et al., 2012). 조장석은 1000~1070 cm−1 구간의 방출도가 1070~1200 cm−1 구간의 방출도보다 작은 것이 특징인데(Milam et al., 2004; Hecker et al., 2010; Donaldson Hanna et al., 2012), 본 연구에서 측정한 조장석의 해당 구간 평균 방출도는 0.88과 0.89로 1000~1070 cm−1 구간에서의 평균 방출도가 작게 측정되었다. 아회장석과 회장석은 회장석의 함량에 따라 구분되지만 구성 성분이 비슷하기 때문에 방출도 특징 또한 유사하다. Figures 2c~d에 보인 바와 같이 아회장석과 회장석의 RB는 700~800 cm−1와 900~1200 cm−1 영역에서 나타났고, 1085 cm−1에서의 방출도는 각각 0.96과 0.97로 측정되었다. 두 광물의 방출도는 1085 cm−1를 기점으로 900~1080 cm−1와 1090~1200 cm−1에서 방출도가 다르게 나타나는 특징을 볼 수 있다. Christensen et al. (2000)은 860 cm−1에서 회장석의 방출도가 더 작다고 보고한 바 있는데, 본 연구에서 측정한 이들의 방출도는 큰 차이를 나타내지 않았다. 이는 본 연구에서 사용한 두 광물 시료의 경우 회장석 함량의 차이가 적기 때문으로 사료된다.
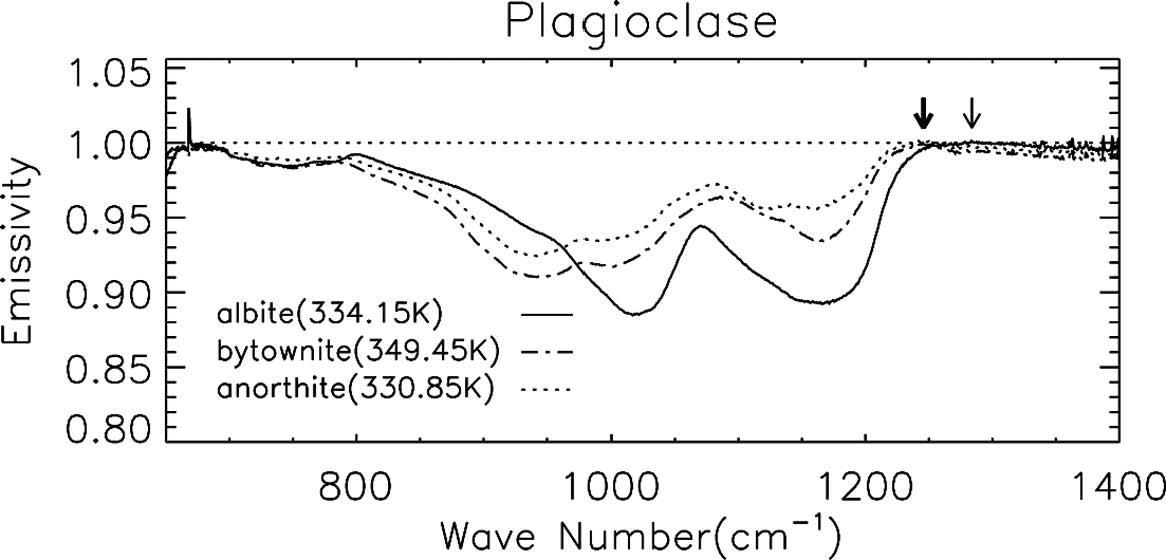
Three emissivity spectra of plagioclase: albite (solid), bytownite (dash-dotted), anorthite (dotted). The thin arrow indicates CF location of albite, while thick arrow indicates CF location of bytownite and anorthite.
Figure 3은 본 연구에서 측정한 사장석(조장석, 아회장석, 회장석)의 방출도를 비교한 것이다. 첫 번째 RB 구간인 700~800 cm−1에서 회장석의 평균 방출도는 0.988, 조장석의 평균 방출도는 0.984, 그리고 아회장석의 평균 방출도는 0.982로 측정되었다. 두 번째 RB가 나타나는 구간은 850~1250 cm−1인데, 방출도 특징을 좀 더 자세히 보기 위해 Milam et al. (2004)과 Donaldson Hanns et al. (2012)가 제안한 것과 같이 RB 구간을 850~1100 cm−1와 1100~1250 cm−1로 구분하여 비교하였다. Table 1에는 첫 번째 RB와 두 번째 RB의 각 소구간에서 최소 방출도를 나타내었다. 파수범위 850~1100 cm−1에서 최소 방출도의 경우 회장석은 0.926, 아회장석은 0.910, 그리고 조장석은 0.884였다. 또한 1100~1250 cm−1에서 최소 방출도는 회장석이 0.955, 아회장석이 0.934 그리고 조장석이 0.892으로 측정되었다. CF는 회장석과 아회장석의 경우 1245.79 cm−1에서 그리고 조장석의 경우 1283.79 cm−1에서 나타났다. 이러한 순서는 선행연구 Milam et al. (2004)과 Donaldson Hanns et al. (2012)의 결과와 일치하는 것이다.
Salisbury and D’Aria (1992)는 석영과 방해석의 방출도 특징이 사암에서도 나타난다고 하였는데, 그 내용은 다음과 같다: (1) 석영의 RB 특징이 나타나며, (2) 760~820 cm−1 구간에서는 방출도가 석영보다 크게 나타나고, (3) 885 cm−1 부근은 CO3에 의한 RB 구간으로 방해석보다 큰 방출도를 보인다. 이러한 특징은 본 연구에서 측정한 사암의 방출도 스펙트럼(Fig. 2e)에서도 관측되었다. 방출도의 파장에 따른 변화를 보면 석영의 경우 1121 cm−1에서 1158 cm−1까지 방출도가 0.685에서 0.802으로 0.117 증가한 반면 사암의 경우 동일한 구간에서 방출도가 0.872에서 0.908로 0.036 증가하였다. 또한 820~900 cm−1에서 석영의 방출도 변화에 비해 사암의 방출도의 변화가 더 작게 측정되었다. 이는 탄산염에 의한 영향으로, Salisbury and D’Aria (1992)가 언급한 사암의 방출도 스펙트럼 특징이 본 연구에서도 유사하게 측정되었음을 알 수 있다.
4.2 오차분석
시료의 온도는 방출도의 계산에서 중요한 인자이기 때문에 시료의 온도를 정확하게 정의하여야 한다. 본 연구에서는 부착 온도계를 이용하여 시료의 온도(Tsamp)를 측정하였지만 부착 위치에 따라 온도가 다르게 나타나는 단점이 발견되었다. Ruff et al. (1997)은 이러한 단점을 보완하기 위하여 CF에서의 방출도가 1이되는 온도(Tcf)를 시료의 온도로 가정하고 방출도를 계산하였다. 본 연구에서도 시료의 온도는 Ruff et al.(1997)의 방법을 사용하여 구하였다.
시료의 온도를 Tsamp 혹은 Tcf로 가정하였을 때, 계산한 방출도의 차이를 보기 위하여 방출도 오차를 다음과 같이 계산하였다.
| (9) |
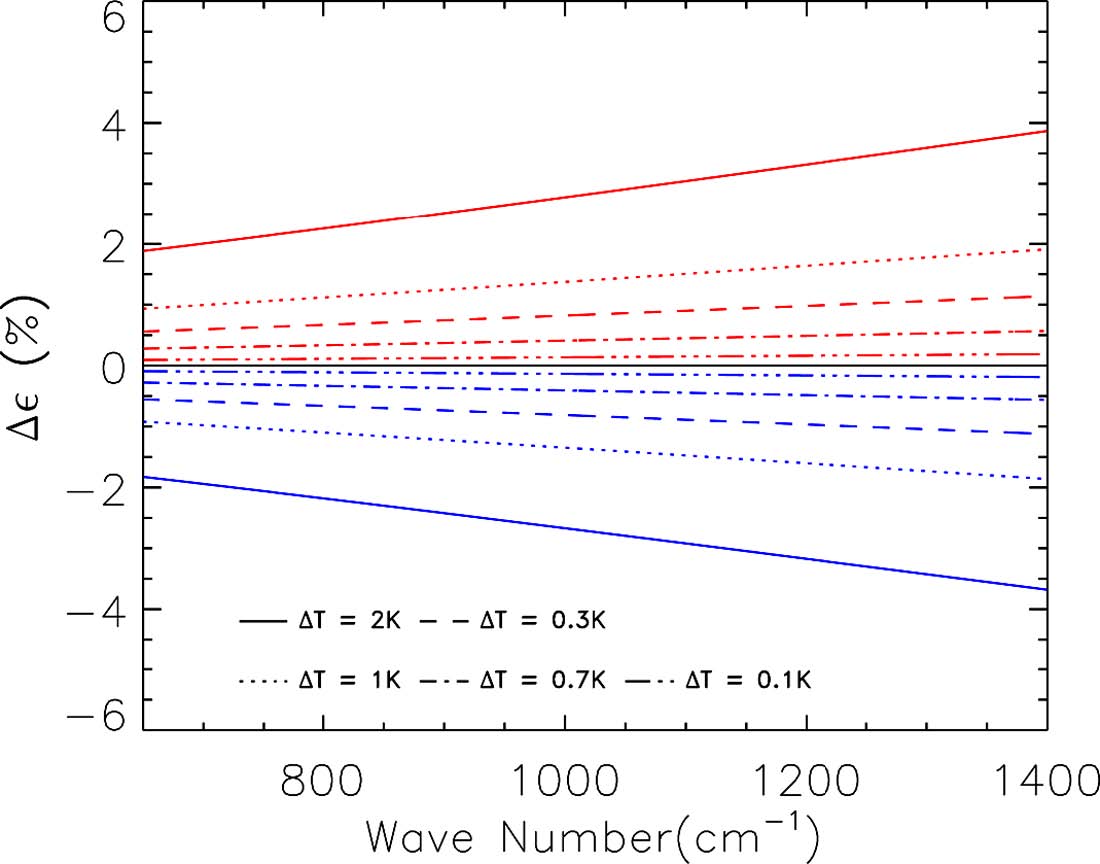
The emissivity error resulting from incorrect temperatures of the sample. Spectral errors are presented as percent change in emissivity from the correct emissivity value.
여기서 ε은 Tcf를 사용하여 계산한 방출도이고, ε*은 Tsamp을 가정하여 계산한 방출도이다.
Figure 4는 ΔT (= Tsamp − Tcf)에 따른 Δε를 파수에 따라 나타낸 그림이다. 붉은 선은 Tsamp < Tcf인 경우이고 파란 선은 Tsamp > Tcf인 경우이다. 파수 650 cm−1에서 ΔT = −1 K일 때 방출도는 1%가 차이가 나며 ΔT=+1K일 때 −1%의 차이를 보인다. 파수 1400 cm−1에서는 2%와 −2%로 Δε (%)의 크기는 ΔT에 따라 그리고 파수에 따라 거의 선형적으로 증가하였다. 식(9)로 정의된 방출도 오차는 근사적으로 다음과 같이 표현된다.
| (10) |
만약 ΔT = 0이면 Δε = 0이 되며, Tsamp과 Tcf가 비슷하여 그 차이가 작은 경우에는 Δε ∝ (hcω/k)(Tcf − Tsamp/TsampTcf)가 되어 오차는 파수에 따라 그리고 |ΔT|에 따라 크기가 증가하게 된다.
Table 2는 본 연구에서 측정한 Tsamp와 방출도 계산에 사용한 Tcf의 온도를 나타낸 것이다. Tsamp와 Tcf의 평균 차이는 0.98 K이며, Tcf을 사용하지 않고 Tsamp을 사용했을 때 계산한 방출도 오차는 1% 내외이다.
4.3 다른 자료와 비교
본 연구에서 측정한 광물의 방출도를 다른 자료와 비교하였다. 여기에서는 ASTER에서 제공하는 Bidirectional 반사도(이하 BR)와 Directional-hemisphere 반사도(이하 DHR) 자료 및 ASU의 반사도 자료에서 구한 방출도와 비교하였다. 물질의 방출도는 구성 성분과 온도에 따라 다르며 반사도는 구성 성분과 온도 뿐만 아니라 표면 상태(예; 고체, 분말, 거칠기)와 측정 방법(예; BR, DHR, Biconical Reflectance)에 따라서도 다르게 나타난다(Salisbury and Walter, 1989; Christensen and Harrison, 1993; Bras and Erard, 2003). 본 연구에서 측정한 평면 광물 시료의 방출도는 비방향성을 가정할 수 있는데, 이러한 비방향성 방출도는 Biconical 반사도에 키르히호프 법칙 식(7)을 적용하여 구한 방출도와 비교하여야 된다(King et al., 2004). 따라서 ASTER의 BR 자료 혹은 DHR 자료에서 구한 방출도와 정량적 비교는 타당하지 않기 때문에 여기에서는 정성적 비교에 중점을 두었다.
Figure 5a는 ASTER 자료에서 구한 방출도와 본 연구에서 측정한 석영의 방출도를 비교한 것이다. ASTER 자료는 크기가 500~1500 mm인 석영 분말의 DHR 자료와 석영 결정체의 BR 자료를 이용하여 계산한 것이다. 분말을 이용한 반사도 측정은 DHR 측정에 유리한 측면이 있으나 산란의 영향을 포함한 Hapke(1981) 이론을 적용해야 하는 어려움이 있다. 그러나 입자의 크기가 파장에 비해 상당히 큰 경우 산란의 영향이 무시되지만, DHR 자료이기 때문에 본 연구에서 측정한 방출도와 정량적 비교는 되지 않는다. 이러한 차이가 있음에도 본 연구에서 측정한 석영의 방출도는 ASTER 자료와 비교했을 때, 석영의 RB 구간인 750~850 cm−1와 1050~1250 cm−1에서 방출도 스펙트럼의 특징은 매우 유사하게 나타났다. 특히 약 1160 cm−1에서 방출도가 크게 증가하였는데, 이것은 석영 방출도의 대표적인 특징이라 할 수 있다.
Figure 5b는 조장석의 결과를 비교한 것이다. 크기가 125~500 μm인 조장석 입자를 측정한 ASTER 자료와 본 연구에서 측정한 조장석의 방출도 스펙트럼은 전 구간에서 그 특징이 일치하였다. RB 구간인 1100~1200 cm−1에서의 방출도는 950~1050 cm−1에서의 방출도보다 크게 나타났다.
Figure 5c는 아회장석에 대한 비교 결과이다. 크기가 710~1000 μm인 입자를 측정한 ASU 반사도 자료에서 계산한 방출도와 비교하였다. 본 연구의 결과와 ASU의 방출도 스펙트럼은 RB 구간의 위치와 파장에 따른 변화가 유사하며, Milam et al. (2004)의 결과와도 그 위치와 파장에 따른 변화 특징이 비슷하다. ASU 자료의 CF는 파수 1210 cm−1에서 나타났으며 본 연구에서 측정한 스펙트럼의 CF는 1245 cm−1 부근에서 나타났다. CF와 RB가 나타나는 영역과 방출도 값의 차이는 시료의 구성 성분, 온도, 그리고 측정 방법의 차이에 기인한 것으로 사료된다.
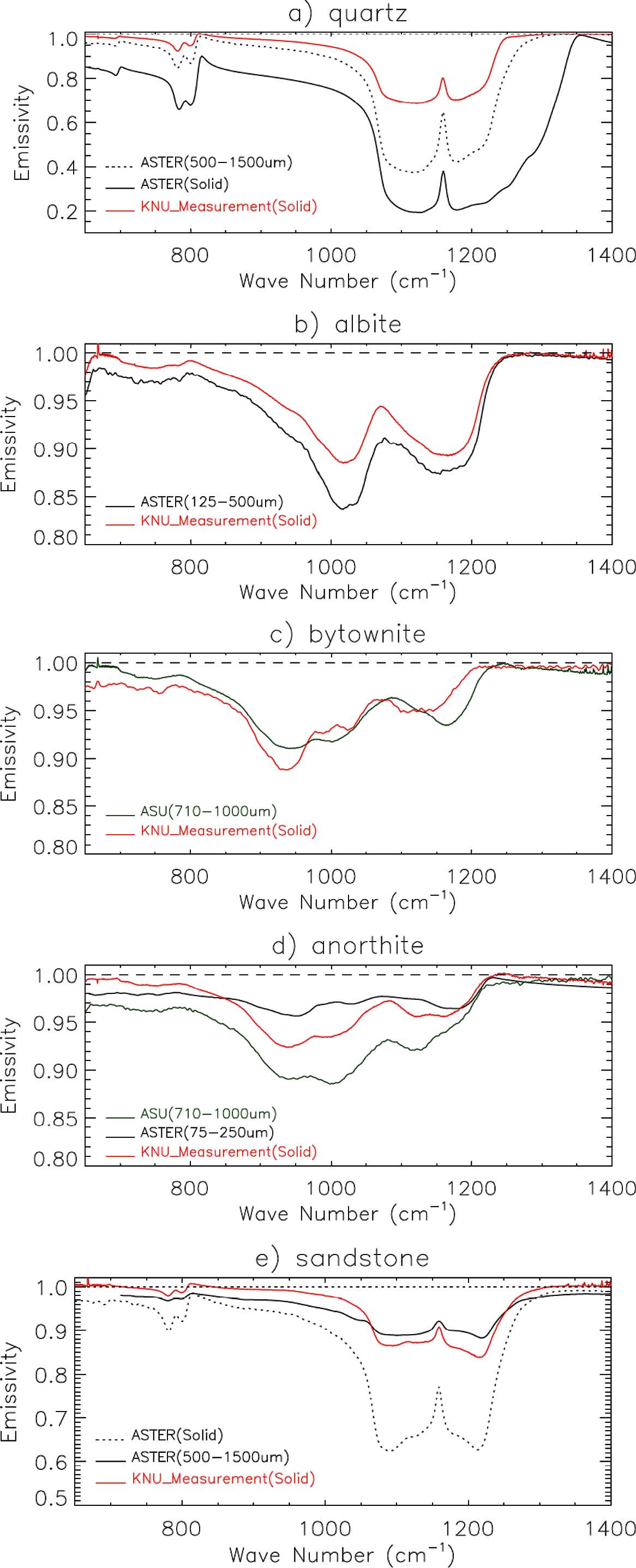
Comparison of emissivity spectra acquired from this study (red) with emissivity spectra acquired by ASTER (black and green) for a) quartz, b) albite, c) bytownite, d) anorthite, and e) sandstone. Emissivity calculated from bidirectional reflectance data and directional-hemisphere reflectance data are indicated by solid line and dotted line, respectively.
Figure 5d는 회장석에 대한 결과를 비교한 것으로 ASTER 자료는 입자의 크기가 75~250 μm인 분말의 BR 자료에서 구한 방출도를 나타낸 것이다. ASU 자료는 크기가 710~1000 μm인 분말에 대한 것이다. 아회장석의 방출도는 RB 구간인 900~980 cm−1에서의 방출도가 1000~1050 cm−1의 방출도보다 작은 특징을 나타내는데(Christensen et al., 2000; Donaldson Hanna et al., 2012), ASU 자료에서는 1000~1050 cm−1의 방출도가 작게 나타났다. ASTER 방출도 스펙트럼에서는 CF가 파수 1220 cm−1에서 나타났고, 본 연구에서 측정한 회장석의 CF는 1245.79 cm−1에서 측정되었다.
Figure 5e은 사암에 대한 비교이다. ASTER 자료는 500~1500 μm 분말의 BR 자료와 결정체의 DHR 자료에서 구한 것이다. 이들 사암의 방출도는 규산염에 의해 나타나는 RB 구간(700~850 cm−1와 1000~1250 cm−1)이 서로 일치하였다. 특히 본 연구의 결과는 ASTER의 500~1500 μm 분말에 대한 자료와 비교하였을 때 방출도가 비슷하며 파장에 따른 변화 특징도 매우 유사하였다.
5. 요약 및 결론
2018년에 발사 예정인 후속 기상위성은 천리안 위성보다 많은 적외 채널이 있으며, 지표 정보를 포함한 다양한 대기의 정보를 산출할 예정이다. 위성의 각 채널로 측정한 빛 에너지를 모의할 때 복사모델에서는 지표 방출도 자료가 중요한 자료로 요구된다. 아쉽게도 국내에서는 지표 물질의 적외영역 방출도에 대한 연구, 특히 방출도 측정에 대한 연구가 미흡하여 본 연구가 이 분야의 첫 시도가 되었다. 현재까지 지표 물질에 대한 자료를 많이 축적하지 못하였기 때문에 본 연구에서는 지표를 구성하고 있는 대표적 광물을 선정하여 방출도를 측정하고 그 특징을 분석하였다.
본 연구에서 방출도 측정에 사용한 FT-IR 간섭계의 NESR은 측정 영역인 650~1400 cm−1에서 10−3 이하의 작은 값이기 때문에, FT-IR 측정 자료는 신뢰할 수 있는 것으로 사료된다. 시료의 온도(Tsamp)와 방출도 계산에 사용된 CF온도(Tcf)의 평균 차이는 0.98 K이며, Tcf을 사용하지 않고 Tsamp을 사용했을 때 계산한 방출도 오차는 1% 내외이다.
온도가 327.15 K인 석영의 방출도에서는 700~850 cm−1와 1050~1250 cm−1 영역에 RB가 나타났다. 해당 구간의 방출도 평균은 0.944와 0.754이다. 이 두 구간을 제외한 파수 영역에서의 평균 방출도는 0.976이며, RB에서의 방출도보다 크게 측정되었다. ASTER 반사도 자료에서 구한 방출도와 비교했을 때 본 연구에서 측정한 석영의 방출도는 크기에서 차이가 있지만 동일한 위치에서 RB가 나타났다. 본 연구에서 측정한 CF는 1337.87 cm−1 부근에서 측정되었으며, 이것은 Christensen and Harrison (1993)과 Wenrich and Christensen (1996)의 결과와 일치하였다. 회장석과 아회장석의 경우 CF가 1245.79 cm−1에서 나타났으며, 조장석의 경우 1283.79 cm−1에서 나타났다. 회장석의 함량이 많을수록 CF가 나타나는 파수가 증가하는 것은 선행연구(Wagner, 2000; Milam et al., 2004; Donaldson Hanna et al., 2012)의 결과와 일치하였다. 온도가 334.35 K인 사암의 방출도 스펙트럼에서는 석영의 RB (700~850 cm−1와 1050~1250 cm−1)와 방해석의 RB (820~900 cm−1)가 나타났다.
본 연구에서는 5개의 시료를 선정하여 측정하였으나 위성 자료에서 산출한 방출도를 검증하거나 정확한 대기의 정보를 산출하기 위해서는 다양한 지표면 구성 물질에 대한 방출도 정보를 축적하여야 할 것으로 사료된다.
Acknowledgments
본 연구는 환경부 차세대에코이노베이션 기술개발사업(2012000160002)의 지원으로 수행되었습니다.
References
-
Baldridge, A. M., S. J. Hook, C. I. Grove, and G. Rivera, (2009), The ASTER spectral library version 2.0, Remote Sens. Environ, 113, p711-715, [Available online at http://speclib.jpl.nasa.gov].
[https://doi.org/10.1016/j.rse.2008.11.007]

-
Bras, A. L., and S. Erard, (2003), Reflectance spectra of regolioth analogs in the mid-infrared: effects of grain size, Planet. Space Sci, 51, p281-294.
[https://doi.org/10.1016/S0032-0633(03)00017-5]

-
Cho, A. R., and M. S. Suh, (2013), Evaluation of Land Surface Temperature Operationally Retrieved from Korean Geostationary Satellite (COMS) Data, Remote Sens, 5, p3951-3970.
[https://doi.org/10.3390/rs5083951]

-
Christensen, P. R., and S. T. Harrison, (1993), Thermal Infrared Emission spectrometer of natural Surfaces: Application to Desert Varnish Coating on Rocks, J. Geophys. Res, 98, p19819-19834.
[https://doi.org/10.1029/93JB00135]

-
Christensen, P. R., J. L. Bandfield, and V. E. Hamilton, (2000), A thermal emission spectral library of rock-forming minerals, J. Geophys. Res, 105, p9735-9739, [Available online at http://speclib.asu.edu].
[https://doi.org/10.1029/1998JE000624]

-
Chunnilall, C. J., and E. Theocharous, (2012), Infrared hemispherical reflectance measurements in the 2.5 μm to 50 μm wavelength region using a Fourier transform spectrometer., Metrologia, 49, p73-80.
[https://doi.org/10.1088/0026-1394/49/2/S73]

-
Conel, J. E., (1969), Infrared emissivities of silicates: Experimental results and a cloudy atmosphere model of Spectral emission from condensed particulate mediums, J. Geophys. Res, 74, p1614-1634.
[https://doi.org/10.1029/jb074i006p01614]

-
Cooper, B. L., J. W. Salisbury, R. M. Killen, and A. E. Potter, (2002), Midinfrared spectral features of rocks and their powders, J. Geophys. Res, 107, p1-7.
[https://doi.org/10.1029/2000JE001462]

-
Donaldson Hanna, K. L., I. R. Thomas, N. E. Bowles, B. T. Greenhagen,, C. M. Pieters, J. F. Mustard, C. R. M. Jackson,, and M. B. Wyatt, (2012), Laboratory emissivity measurements of the plagioclase solid solution series under varying environmental conditions, J. Geophys. Res, 117, pE11004..
[https://doi.org/10.1029/2012JE004184]

-
Hapke, B., (1981), Bidirectional reflectance spectroscopy, 1: Theory, J. Geophys. Res, 86, p3039-3054.
[https://doi.org/10.1029/JB086iB04p03039]

-
Hecker, C., M. van der Mdijde, and F. D. van der Meer, (2010), Thermal infrared spectrometer on feldspars - Successes, limitations and their implications for remote sensing, Earth Sci. Rev, 103, p60-70.
[https://doi.org/10.1016/j.earscirev.2010.07.005]

-
Henderson, B. G., P. G. Lucey, and B. M. Jakosky, (1996), New laboratory measurements of mid-IR emission spectra of simulated planetary surfaces, J. Geophys. Res, 101, p14969-14975.
[https://doi.org/10.1029/96JE01089]

-
Hulley, G. C., and S. J. Hook, (2009), Intercomparision of versions 4, 4.1 and 5 of the MODIS Land Surface Temperature and Emissivity products and validation with laboratory measurements of sand samples from the Namib desert, Namidia, Remote Sens. Environ, 113, p1313-1318.
[https://doi.org/10.1016/j.rse.2009.02.018]

- Hwang, J. Y., M. I. Jang, J. S. Kim, W. M. Cho, B. S. Ahn, and S. W. Kang, (2000), Mineralogy and chemical composition of the residual soils from South Korea, J. Miner. Soc. Korea, 13, p147-163.
-
Ishii, J., and A. Ono, (2001), Uncertainty estimation for emissivity measurements near room temperature with a Fourier transforms spectrometer, Meas. Sci. Technol, 12, p2103-2112.
[https://doi.org/10.1088/0957-0233/12/12/311]

-
Jeong, G. Y., (2008), Bulk and single-particle mineralogy of Asian dust and a comparison with its source soils, J. Geophys. Res, 113, p429-467.
[https://doi.org/10.1029/2007JD008606]

-
Johnson, J. R., F. Hörz, P. G. Lucey, and P. R. Christensen, (2002), Thermal infrared spectrometer of experimentally shocked anorthosite and pyroxenite: Implications for remote sensing of Mars, J. Geophys. Res, 107, p1-14.
[https://doi.org/10.1029/2001JE001517]

- King, P. L., M. S. Ramsey, P. F. McMillan, and G. Swayze, (2004), Laboratory Fourier transform infrared spectroscopy methods for geologic samples, In Infrared Spectroscopy in Geochemistry, Exploration Geochemistry and Remotesening, King P. L. , M. S. Ramsey, and G. Swayze Eds, Mineral. Assoc, p57-92.
-
Korb, A. R., J. W. Salisbury, and D. M. D’Aris, (1999), Thermal-infrared remote sensing and kirchhoff’s law 2. Field measurements, J. Geophys. Res, 104, p15339-15350.
[https://doi.org/10.1029/97JB03537]

-
Mathew, G., A. Nair, T. K. Gundu Rao, and K. Pande,, (2009), Laboratory technique for quantitative thermal emissivity measurements of geological samples, J. Earth System Science, 118, p391-404.
[https://doi.org/10.1007/s12040-009-0035-4]

-
Milam, K. A., H. Y. McSween, V. E. Hamilton, Moersch, J. M., and P. R. Christensen, (2004), Accuracy of plagioclase compositions from laboratory and Mars spacecraft thermal emission spectra, J. Geophys. Res, 109, p1-16.
[https://doi.org/10.1029/2003JE002097]

-
Nerry, F., J. Labed, and M. P. Stoll, (1990), Spectral Properties of Land Surfaces in the Thermal infrared 1. Laboratory Measurements of Absolute spectral Emissivity Signatures, J. Geophys. Res, 95, p7027-7044.
[https://doi.org/10.1029/JB095iB05p07027]

-
Norman, J. M., and F. Becker, (1995), Terminology in thermal infrared remote-sensing of natural surfaces, Agric. Forest Meteor, 77, p153-166.
[https://doi.org/10.1016/0168-1923(95)02259-Z]

-
Qin, Z., and A. Karnieli, (1999), Progress in the remote sensing of land surface temperature and ground emissivity using NOAA-AVHRR data, Int. J. Remote Sens, 20, p2367-2393.
[https://doi.org/10.1080/014311699212074]

-
Revercomb, H. E., H. Buijs, H. B. Howell, D. D. Laporte, W. L. Smith, and L. A. Sromovsky, (1988), Radiometric calibration of IR Fourier transform spectrometers: solution to a problem with the High-Resolution Interferometer Sounder, Appl. Opt, 27, p3210-3218.
[https://doi.org/10.1364/ao.27.003210]

-
Ruff, S. W., P. R. Christensen, and P. W. Barbera, (1997), Quantitative thermal emission spectrometer of minerals: A laboratory technique for measurement and calibration, J. Geophys. Res, 102, p14899-14913.
[https://doi.org/10.1029/97JB00593]

-
Salisbury, J. W., and L. S. Walter, (1989), Thermal infrared (2.5~13.5 μm) Spectroscopic Remote Sensing of Igneous Rock Types on Particulate Planetary Surfaces, J. Geophys. Res, 94, p9192-9202.
[https://doi.org/10.1029/JB094iB07p09192]

-
Salisbury, J. W., and D. M. D’Aria, (1992), Emissivity of Terrestrial Materials in the 8~14 μm Atmospheric Window, Remote Sens. Environ, 42, p83-106.
[https://doi.org/10.1016/0034-4257(92)90092-X]

-
Salisbury, J. W., A. Wald, and D. M. D’Aria, (1994), Thermal- infrared remote sensing and Kirchhoff's law 1. Laboratory measurements, J. Geophys. Res, 99, p11891-11911.
[https://doi.org/10.1029/93JB03600]

-
Schmugge, T., S. J. Hook, and C. Coll, (1998), Recovering Surface Temperature and Emissivity from Thermal Infrared Multispectral Data, Remote Sens. Environ, 65, p121-131.
[https://doi.org/10.1016/S0034-4257(98)00023-6]

- Sen, G., (2001), Earth’s Materials: Minerals and Rocks, Prentice Hall, p560.
- Wagner, C., (2000), Thermal Emission spectrometer of Laboratory Regoliths, Astron. Soc. Pac. Conf. Ser, 196, p233-247.
-
Wenrich, M. L., and P. R. Christensen, (1996), Optical constants of minerals derived from emission spectrometer: Application to quartz, J. Geophys. Res, 101, p15921-15931.
[https://doi.org/10.1029/96JB01153]