접합대순환모형의 초기조건 생산방법에 따른 북반구 겨울철 기온과 해수면 온도의 계절 예측성 비교 연구

1. 서 론

접합대순환모형(Coupled General Circulation Model, CGCM)은 지구시스템 내에서 일어나는 기후를 이해하고 장기기후를 예측하기 위한 주요한 수단이다(IPCC, 1990). 하지만 자연의 혼돈적 성질로 인해 모형의 예측결과는 아직까지 많은 불확실성을 지니고 있다(Charney, 1951; Lorenz, 1963; IPCC, 2007). 만약 모형이 기후의 물리 · 역학적 과정을 완벽하게 표현한다해도 초기 및 경계조건에서 오는 불확실성으로 인해 모형의 예측 성능에는 한계가 있다. 선행연구들은 모형의 예측결과에 불확실성을 줄이기 위해 모형의 해상도를 조밀하게 만들거나(e.g., Guilyardi et al., 2004), 모형 내의 물리적 과정에 대한 모수화(parameterization)를 개선하였다(e.g., Gregory et al., 2000; Collins et al., 2001; Kiehl and Gent, 2004). 초기조건에 대한 불확실성을 줄이기 위한 다른 방안으로는 초기 조건에 섭동을 주거나(Houtekamer and Derome, 1995; Stensrud et al., 2000) 모델의 초기 시간(Lu et al., 2007) 및 물리적 과정(Stensrud et al., 1999)을 다르게 해 다수의 앙상블 멤버를 구성하는 앙상블 방법이 있다.

모형의 예측성을 개선하기 위한 또 하나의 방안으로는 모형에 제공되는 초기조건을 통계 및 역학적 방법을 이용하여 더욱 현실적으로 초기화하여 모형에 제공하는 방법이 있다(Alves et al., 2004; Balmaseda and Anderson, 2009). 세계 여러 현업기관(operational center)에서도 계절 예측성을 향상시키기 위하여 모델의 물리적 과정과 해상도를 개선하는 것 외에도 접합대순환모형 초기조건의 질을 향상시켜 모형의 예측성을 개선하고 있다(e.g., Wang et al., 2001; Palmer et al., 2004; Saha et al., 2006; Molteni et al., 2011; Kim et al., 2012; Saha et al., 2014). 세계 현업기관 중 하나인 NCEP (National Centers for Environmental Prediction)에서 운영중인 NCEP CFSv2 (Climate Forecast System Version 2)의 경우 대기-지면-해양-해빙에 초기조건을 자료동화 방법을 이용하여 초기화시켜 계절 예측 성능을 개선하였을 뿐만 아니라 자료동화에 들어가는 재분석 자료를 대기-해양-빙-지면이 결합된 재분석 자료(Climate Forecast System Reanalysis, CFSR)로 새롭게 만들어 개선 시켜서 계절 예측 성능을 향상시키고 있다(Saha et al., 2010, 2014).

본 연구에서는 접합대순환모형 초기조건 가운데 지면 초기조건과 해양 초기조건 생산방법에 따른 북반구 겨울철 기온과 해수면 온도 예측 성능을 살펴보고자 하였다. 접합대순환모형의 지면 초기조건 생성 방법에는 단순히 재분석자료와 기후값을 넣어주는 방법과 AMIP type 적분을 통해 만드는 방법, 그리고 GLACE (Global Land-Atmosphere Coupling Experiment)에 사용된 실험설계와 같이 land surface 모형을 offline형식으로 적분하여 지면 초기조건으로 사용하는 방법 등이 있다(Gates, 1992; Koster et al., 2009; Wang et al., 2009; Sun and Ahn, 2014). 특히 GLACE는 11개의 유수기관들의 모형들을 통해 토양수분의 초기화가 지표변수인 기온과 강수의 sub-seasonal (2-month) 예측성에 영향 미친다는 것을 보였다(Koster et al., 2011). AMIP type의 적분을 이용한 방법은 Atmospheric General Circulation Model (AGCM)에 관측된 경계장(e.g., 해수면 온도)을 넣어주면서 대기와 지면이 상호작용하면서 연속적으로 적분을 수행하는 것으로 NCEP 등에서 운영하는 역학적 계절예측 시스템 방안으로 사용한 바 있다(Ji et al., 1998). 본 연구에서는 AMIPtype 적분 결과를 이용하여 바로 사용했을 때와 기후값으로 생성하여 사용했을 때에 계절 예측성이 미치는 영향을 보고자 하였다.

해양 초기조건의 경우 자료동화 유무에 따른 계절 예측성 변화를 살펴보고자 하였다. 자료동화 방법은 초기조건의 개선을 위한 효과적인 방법으로 활발히 연구되었다. 앞에서 언급되었지만, 최근 현업기관에서는 자료동화 방법을 이용하여 대기-지면-해양-해빙까지 사용되고 있다. 자료동화는 관측과 모형자료를 결합하는 방법으로 관측과 유사하면서 모형의 기후에 동화된 분석장을 생산하는 방법이다. 자료동화에는 Kalman Filter, optimal interpolation, adjoint-based inverse technique, three-dimensional variational data assimilation (3DVAR), for-dimensional variational data assimilation (4DVAR) 등 다양한 방법이 있다(e.g., Ghil and Malanotte-Rizzoli, 1991; Wunsch, 1996; Bennett, 2002; Dommenget et al., 2004; Wikle and Berliner, 2007; Yang et al., 2009). 본 연구에서는 변분법의 하나인 필터를 이용한 변분법(Variational Analysis using a Filter, VAF)을 자료동화 방법으로 사용하였다. 해수면만 자료동화하여 적분한 결과보다는 표면 아래까지 자료동화한 결과가 ENSO 발달과정을 더 잘 모의한다는 선행연구를 바탕으로(Alves et al., 2004), 해양의 전체 층에 대하여 자료동화를 수행하였다. 대기 초기조건의 경우 AMIP-type 적분에서 얻은 정보를 사용하면 모델이 열대지역 계절안 변동성(tropical intraseasonal variability)을 잘 모의하지 못한다는 선행연구의 결과에 따라(e.g., Reichler and Roads, 1999; Kessler and Kleeman, 2000; Hendon et al., 2007; Shi et al., 2009) 재분석자료를 초기조건으로 사용하되, 이 초기조건에서 발생하는 모델 내에 충격을 피하기 위해 하루의 spin-up을 수행하였다(Anderson and Ploshay, 2000). 보다 자세한 방법에 대한 설명은 2장에서 설명하였다.

2. 자료 및 연구방법

2.1 모형 설명

본 연구에 사용된 모형은 PNU CGCM (Pusan National University Coupled general circulation model)이다(Sun and Ahn, 2011, 2014). Asia-Pacific Economic Cooperation (APEC) Climate Center (APCC)의 장기예측을 위한 다중모델 앙상블(Multi-model Ensemble) 시스템에 참여한 모형인 PNU CGCM은 NCEP Community Climate Model version 3 (CCM3 T42, Kiehl et al., 1996; Hurrel et al., 1998) AGCM, GFDL Modular Ocean Model version 3 (MOM3, Pacanowski and Griffies, 1998) OGCM, Los Alamos National Laboratory (LANL) Elastic-Viscous-Plastic (EVP) Sea-Ice Model (Ahn et al., 2001)로 구성된다(http://www.apcc21.net/eng/html/hapcc030001.html). 대기 성분 모형인 CCM3는 2.8125^o의 수평 해상도를 가지고 있으며, 연직으로는 18층으로 구성되어 있다. 해양 성분모형인 MOM3는 대기 성분모형과 같은 2.8125^o의 경도방향의 수평 해상도를 가지고 있으며, 위도방향으로는 조밀한 가변격자(30^o 아래의 저위도에서는 0.7^o, 30^o~60^o 사이의 중위도에서는 1.4^o, 60^o 이상의 고위도에서는 2.8^o이고 연직은 40층으로 구성되어 있다. PNU CGCM에 대한 설명은 Table 1에 나타내었다.

모델 검증을 위한 관측자료로는 National Centers for Environmental Prediction and the National Center for Atmospheric Research (NCEP/NCAR)에서 제공하는 updated reanalysis2를 사용하였다(Kanamitsu et al., 2002). 이 자료에서 사용된 변수는 기온(2m air temperature, T2m)과 토양수분(soil moisture)이며, T63 gaussian grid (192 × 94)의 격자 자료이다. 또한 경도와 위도방향의 수평해상도가 1.0를 가진Hadley Centre Sea Surface Temperature (HadISST, SST) 자료도 분석을 위해 사용하였다(Rayner et al., 2003). 해양내부의 수온 분포 비교에는 NCEP에서 제공하는 전구 해양자료동화 시스템(Global Ocean Data Assimilation System, GODAS) 자료를 사용하였다(Behringer et al., 1998).

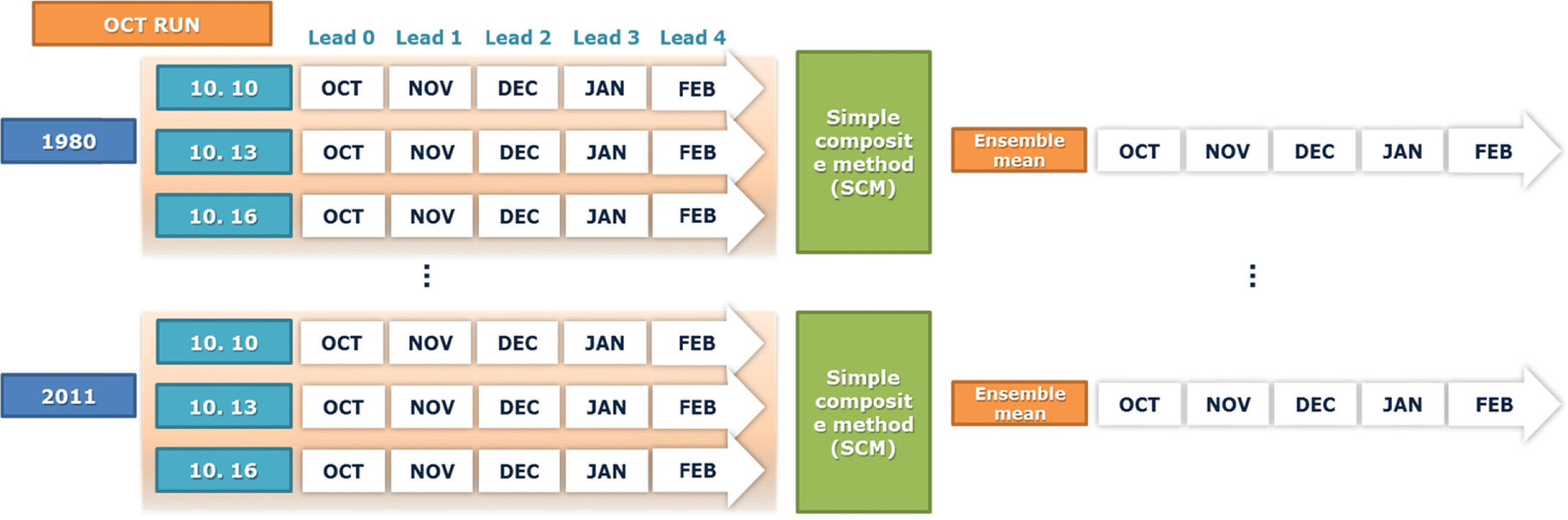
본 연구에서는 초기조건에 따른 모형의 불확실성을 줄이기 위하여 앙상블 예보를 사용하였다(Fig. 1). 앙상블 예보는 서로 다른 초기조건들에 의해 초기화된 앙상블들을 평균하여 초기조건이 가지는 오차에서 기인된 예측의 불확실성들을 줄일 수 있는 방법으로 알려져 있다(Kharin et al., 2001). 앙상블 멤버를 만들기 위해 사용한 방법은 시간지연방법(time lag method)이다. ECMWF의 extended range prediction에 사용된 이 방법은 초기조건의 시간을 다르게 하여 앙상블 멤버를 만드는 방법으로, 효과적으로 앙상블 멤버를 만들어 초기조건에 불확실성을 줄이는 방법이다(Branković et al., 1990). 본 연구에서는 시간지연방법을 이용하여 대기, 지면, 해양 등 CGCM 초기조건에 대하여 각각 3개(10월의 10, 13, 16일)의 앙상블 멤버를 만들었다. 여기서 각 앙상블 멤버들은 동일한 초기조건 시간들끼리 수행되었으며, 최종적으로 각 멤버들의 결과를 simple composite method (SCM)을 이용하여 평균한 후 그 결과의 예측성을 비교하였다. Figure 1과 같이 매 해의 10월 중순(해당되는 앙상블 멤버 날짜)에 모형의 적분을 시작하였고, 모형의 적분 lead time은 5개월(October to February)이다. 1980년부터 2011년까지 총 32년의 자료를 생산하였으며, 각 lead time(month) 및 겨울철(DJF) 기온과 해수면 온도 예측성을 분석하였다.

Table 1.

Component models and resolution of the PNU CGCM.

Fig. 1.

Schematic diagram of PNU CGCM ensemble system.

Fig. 2.

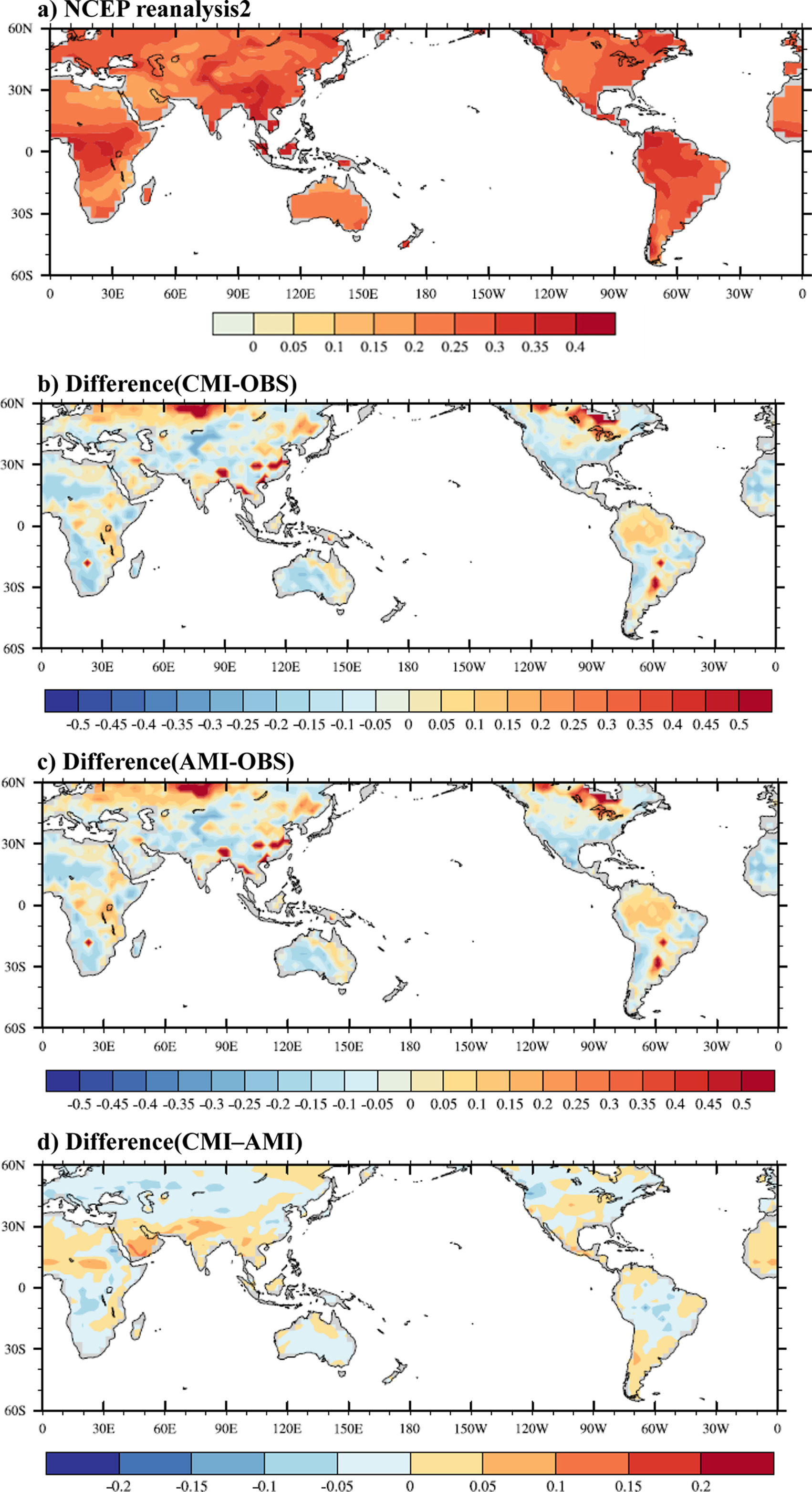
Soil moisture climatology of a) NCEP reanalysis2, differences of b) CMI and c) AMI from NCEP reanalysis2 climatology, difference between d) CMI and AMI.

Fig. 3.

Timeseries of global mean soil moisture of OCT land initial condition per every year from a) CMI and b) AMI in each level.

2.2 지면 및 대기 초기장 생산

본 연구에서는 접합대순환모형의 지면 초기조건 생산을 위하여 AMIP-type 적분을 이용하였다. AMIPtype 적분은 대기 모형에 관측된 대기 상태를 처음 한번만 초기조건으로 입력하고 관측된 SST를 경계조건으로 하여 연속적으로 적분을 수행하는 것이다. 즉, 경계조건으로 주어진 관측된 해양정보에 따라 모형내에서의 대기 및 지면 상태가 동화되도록 한다. 본 연구에서는 지면 초기조건 생산을 위해 PNU CGCM의 대기 성분 모형인 CCM3를 사용하였으며, 1978년 9월 재분석 자료 초기조건 및 경계조건을 이용하여 2012년까지 적분을 이어왔다. 지면 초기조건에 따른 예측성 비교를 위해 AMIP-type 적분 결과를 바로 사용한 경우와 AMIP-type 적분 결과의 기후값을 사용한 경우로 나누어서 실험하였다. 여기에서의 기후값은 32년간에(1980~2011) 10월의 평균값이다. 간단히 표현하기 위하여 AMIP-type 적분으로 만든 지면 초기조건을 AMI, 기후값으로 만든 지면 초기조건을 CMI라 하였다.

대기 초기장의 경우 AMIP-type 적분 결과를 사용하면 열대지역 계절안 변동성을 잘 모의하지 못한다는 선행연구를 바탕으로 NCEP updated reanalysis2 재분석자료를 초기조건으로 사용하되, 적분과정에서 발생하는 모델 내의 충격을 피하기 위해 대기성분모형(CCM3)을 이용하여 하루의 spin-up을 수행하였다. 이 때 대기 변수와 지면 변수 사이에 균형을 맞추기 위해 지면 초기조건도 함께 넣어 spin-up을 수행하였다. 예를 들어 2000년 10월 16일의 접합대순환모형의 대기와 지면초기조건을 만들기 위한 대기성분모형(CCM3)적분의 초기조건으로 AMI은 AMIP-type 적분 결과 중 2000년 10월 15일 자료를 사용하였고, CMI는 10월 기후값을 사용하였다. 대기 초기조건의 경우 2000년 10월 15일 재분석 자료를 이용하였으며, 하루의 spinup 적분을 수행하여 2000년 10월 16일 지면과 대기 초기조건을 만들었다. 즉, 접합대순환모형의 입력자료로는 최종적으로 하루 spin-up으로 생성된 지면과 대기초기조건이 사용되었다.

Figure 2는 재분석 자료와 AMI, CMI으로 생성된 접합대순환 모형의 10월 지면초기장의 최상의 층(10 cm) 토양수분의 기후값 및 기후값 차이 분포를 나타낸 것이다. AMI와 CMI의 최상의 층 토양수분 기후값은 재분석 자료의 차이가 서로 유사하게 나타났다(Figures 2b와 c). 즉, 남아메리카, 캐나다 북동쪽, 중국 등과 같은 지역에서 토양수분이 재분석 자료에 비해 많이 나타나고 있으며 미국과 카자흐스탄 등 지역에서는 토양수분이 적게 나타나는 등 공간적 패턴이 유사하게 나타났다. Figure 2d는 CMI와 AMI의 토양 수분 차이를 나타낸 그림으로, CMI는 AMI에 비하여 적도를 포함한 북위 30^oN까지 토양수분을 많이 나타내고 있으며 30^oN 이상되는 유라시아 대륙에서는 토양수분을 적게 나타내고 있다. CMI이 AMI의 기후값으로 만들어졌음에도 불구하고 이러한 토양수분 차이를 보이는 이유는 최종적으로 생상된 접합모형의 지면초기조건이 CCM3에서 대기초기조건과 함께 하루의 spin-up을 통해 얻어진 결과이기 때문이다.

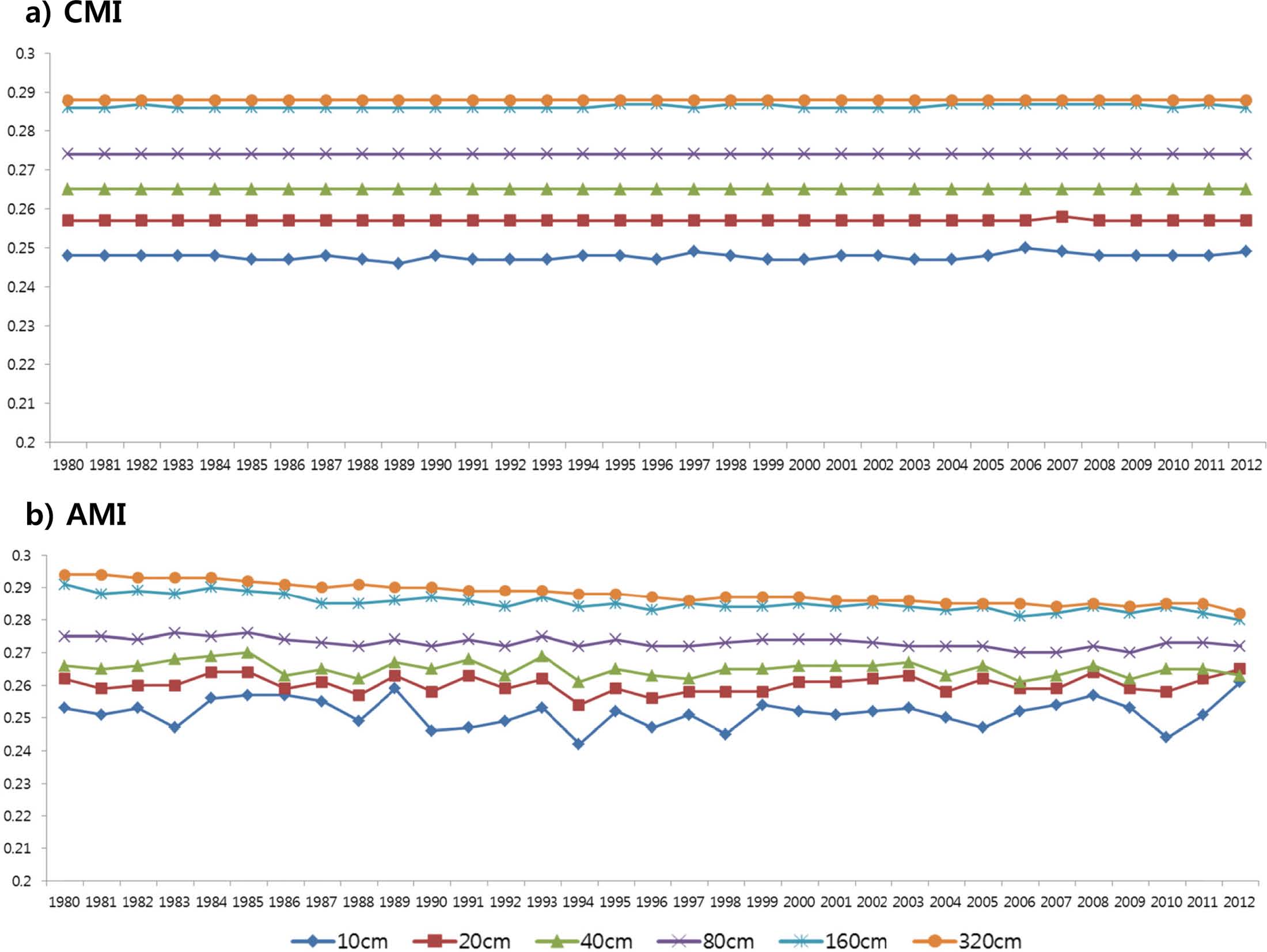
Figure 3는 Fig. 2에서 나타낸 토양수분의 전구 평균값을 각 지면 층별로 나타낸 시계열이다. CMI는 10~20 cm를 제외하고 나머지 층에서는 시간에 따른 변동성이 나타나지 않고 일정한 결과를 보지만, AMI의 경우 10 cm의 최상의 층에서 320 cm의 최하층까지 토양수분의 변동성이 나타난다. 이는 CMI의 경우 지면초기조건을 기후값을 이용하여 하루의 spin-up으로 만들었기 때문에, 지면 최상층에만 변동이 있을 뿐 하층에는 그대로 기후값이 사용되었음을 나타낸다. 반면 AMI 지면 초기조건은 연속적으로 적분된 자료로 생성된 초기조건이기 때문에 CMI와는 달리 모든 지면층에서 시간에 대한 변동성이 나타나고 있다. 하지만 AMIP-type 적분은 관측된 SST를 경계조건으로 하여 연속적으로 적분을 수행하기 때문에, 내륙 깊은 곳, 고위도 등 대기-해양 상호작용, 원격상관에 의한 영향이 미치지 않는 곳에서의 지면 초기조건은 초기화 효과를 크게 기대하기 힘든 한계가 있다.

Fig. 4.

Temporal correlation coefficient maps of SST between observation and a) noDA, b) DA OCT ocean initial conditions. The values at the top left of each figure (a~b) are the global mean TCC.

2.3 해양 초기장 생산

본 연구에서는 최적화된 접합대순환모형 해양 초기 조건 생산을 위하여 자료동화방법을 이용하였다. 여기서의 자료동화방법으로는 변분법의 하나인 필터를 이용한 변분법(Variational Analysis using a Filter, VAF)을 선택하였다(Huang, 2000; Ahn et al., 2005; Ahn et al., 2012b). 이는 관측과 모형의 비용함수를 고려한 방법으로, 비용함수가 최저가 되는 점의 가중치를 사용해 모형과 관측을 동화시켜 준다. 해양 초기조건이 가지고 있는 40층에 대하여 자료동화를 적용하였으며, 자료동화에 사용되는 해양 초기조건 내에 변수는 해양온위(potential sea temperature)와 염도(salinity)이다. 간단히 표현하기 위해 자료동화가 적용된 초기조건을 DA, 적용되지 않는 경우를 noDA이라고 하였다. 자료동화를 위해 사용된 재분석 자료는 계절예측에 실시간 적용하기 위하여 자료의 업로드가 빠른 전구 해양 자료동화시스템(GODAS)자료이다.

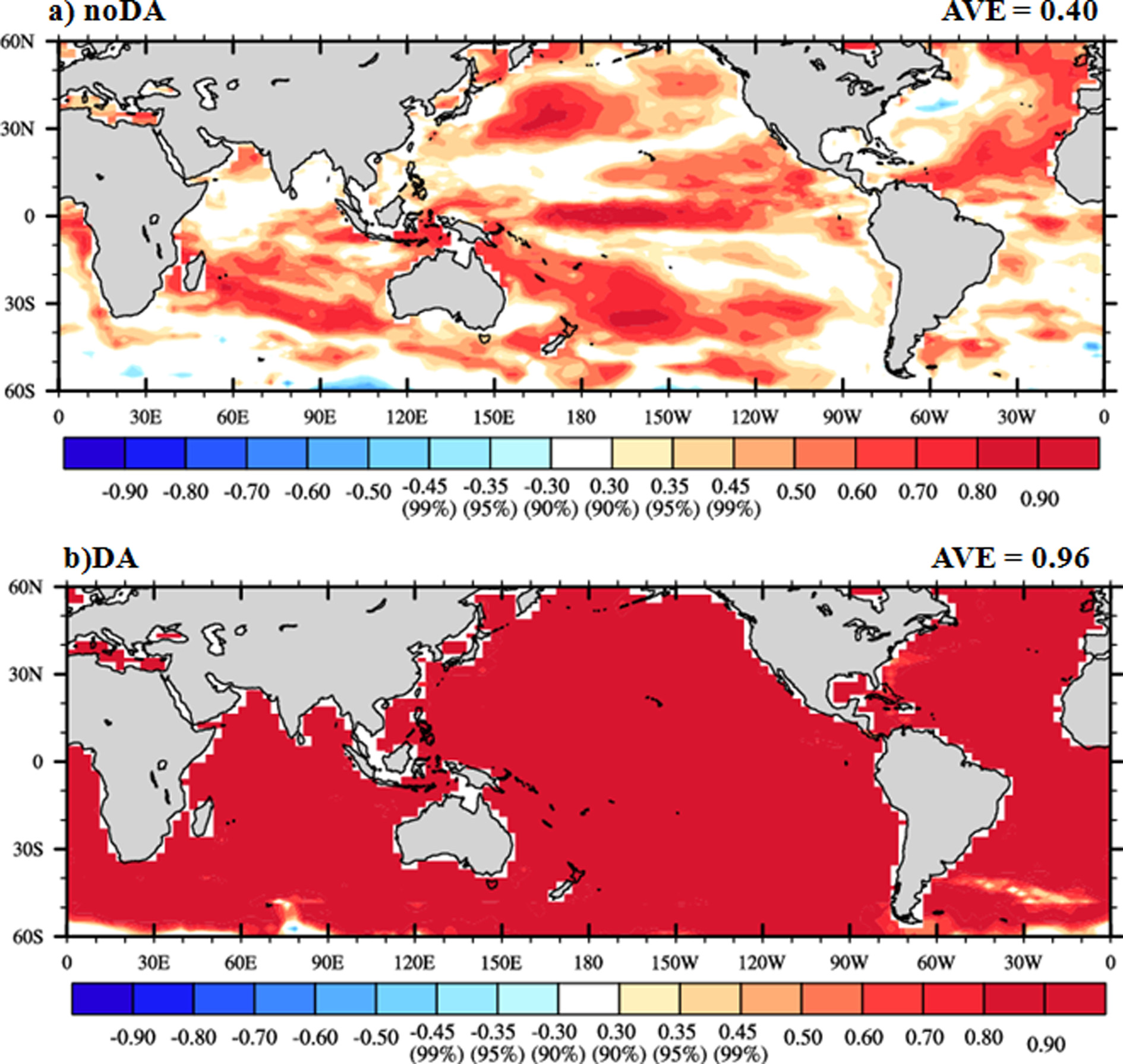
Figure 4는 SST에 대하여 재분석 자료(GODAS)와 각 해양 초기조건(noDA와 DA)들 간에 시간상관(Temporal correlation coefficient, TCC)를 나타낸 것으로 90% 이상 신뢰구간에 유의한 점들에 색칠을 하였다. 이는 자료동화 전후의 해양 초기조건 정확도를 확인해 보기 위한 것으로 noDA는 면적평균(0^o~360^oE, 60^oS~60^oN)값이 0.40인 반면, DA 해양 초기조건은 0.96이었다. 이는 자료동화 후 해양 초기조건이 자료동화 전보다 모든 영역에 대하여 재분석 자료(GODAS)와 매우 높은 시간 상관성을 보임을 알 수 있다.

Table 2.

Model experiments.

3. 실험결과

본 연구에서는 초기조건 생산방법에 의한 북반구 겨울철 예측성 차이를 보기 위하여, Table 2와 같이 실험을 4가지로 나누어서 수행하였다. 각 실험은 CMI와 noDA 초기조건을 이용한 경우(EXP1)와 CMI와 DA 초기조건을 사용한 (EXP2) 경우, AMI와 noDA를 초기조건으로 이용한 경우(EXP3)와 AMI와 DA를 초기조건으로 사용한 경우(EXP4)로 분류된다. 이렇게 분류된 4가지 초기조건을 이용하여 PNU CGCM에 나타나는 북반구 겨울철(DJF) 예측성을 비교하였다. 분석변수는 T2m와 SST이고, 분석기간은 1980~2011년 32년이다. 본 연구에서는 아래와 같이 평균부분과 편차부분으로 분류하여 분석을 편차부분을 이용하여 분석하였다. 이는 평균을 제거함으로써 모형이 가지는 계통적 오차(systematic bias)를 손쉽게 제거할 수 있기 때문이다(Ahn et al., 2012a).

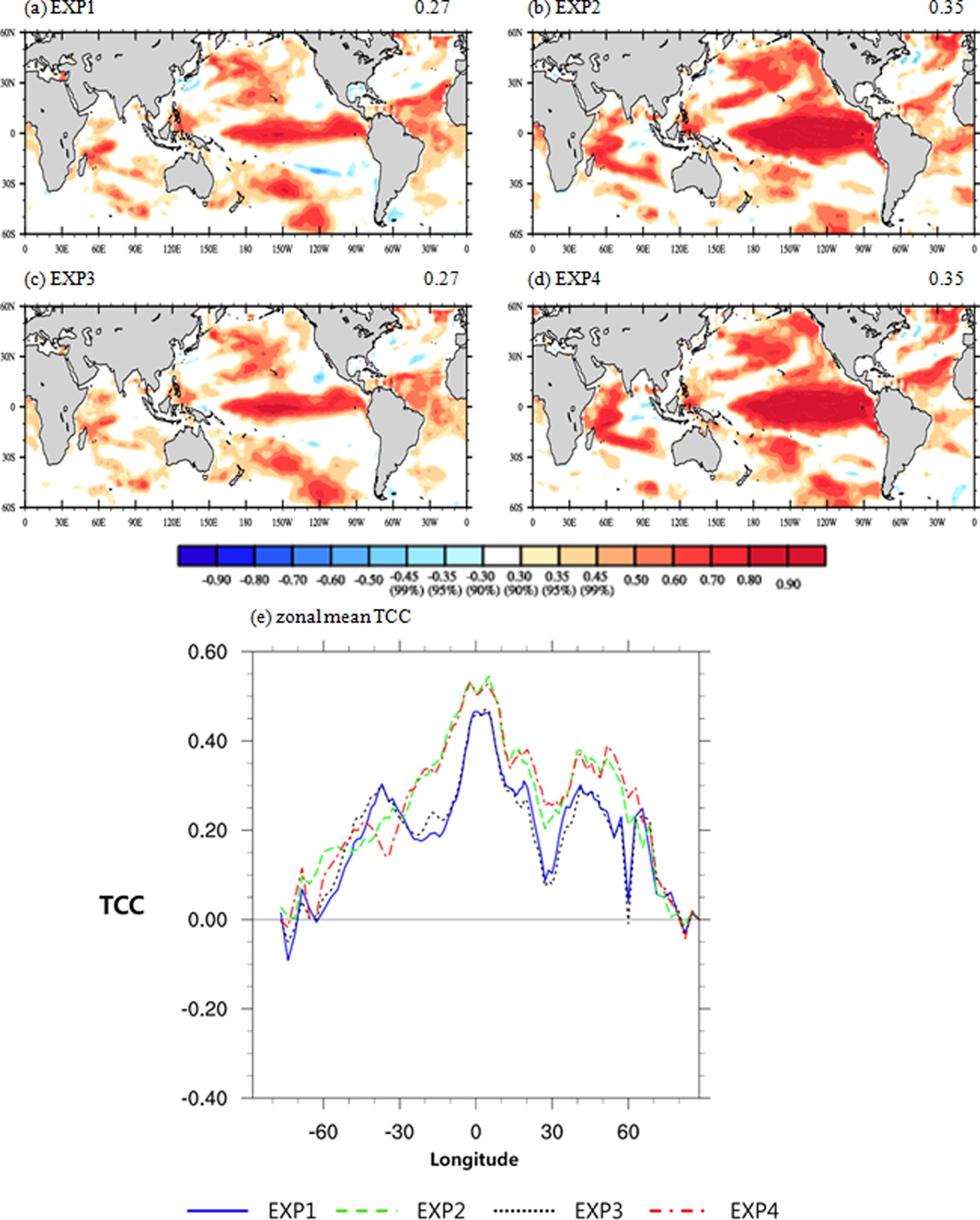
Figure 5는 T2m와 SST의 lead time (month)에 따른 TCC 면적평균(0^o~360^oE, 50^oS~50^oN)값을 나타낸 것이다. 파란색, 녹색, 검정색, 빨간색은 순서대로 EXP1, EXP2, EXP3, EXP4의 결과이다. 두 변수 모두 자료동화가 적용된 EXP2와 EXP4의 결과가 적용되지 않은 EXP1과 EXP3에 비하여 높은 TCC를 나타낸다. 반면 CMI와 AMI를 사용한 EXP1 (EXP2)과 EXP3 (EXP4) 결과 차이는 두 변수 모두 큰 차이가 없지만, SST 보다는 T2m에서 lead time (month)이 길어줄수록 CMI와 AMI의 TCC 차이가 조금씩 증가했다. T2m의 경우 자료동화가 적용되지 않은 실험에서는 10월까지(lead0) TCC가 90% 신뢰구간에 유의하였고, 자료동화가 적용된 실험에서 12월까지(lead0-2) TCC가 유의하였다. SST는 자료동화가 적용됨에 따라 11월(lead0-1)에서 1월까지(lead0-3) 90% 신뢰구간에 유의한 TCC의 lead time (month)이 늘어났다. 보다 상세히 살펴보기 위하여 Figs. 6과 7에서는 T2m와 SST의 각 실험별 북반구 겨울철(DJF)에 따른 TCC 공간 패턴과 동서평균값을 나타내었다. 각 그림에 왼쪽 상단에 위치한 값은 면적평균(0^o~360^oE, 60^oS~60^oN)값으로, T2m의 경우 자료동화를 적용한 EXP2와 EXP4가 0.24, 0.25로 자료동화를 적용하지 않은 EXP1와 EXP3에 비하여 약 0.06~0.08 증가됨을 보였다. 반면 AMI와 CMI 같이 지면 초기조건 차이로 인한 TCC의 값차이는 0.01 정도로 나타났다. SST의 경우에도 자료동화 적용여부에 따라 TCC의 차이가 0.08이 났으며, 지면 초기조건 차이에 따라서는 면적평균값으로는 그 차이가 나타나지 않을 만큼 작았다. 이는 지면 초기 조건보다는 해양 초기조건이 지배적으로 계절 예측성능에 영향을 미치는 것을 알 수 있다. 이러한 결과는 지면 초기조건의 영향은 적분이 시작되고 급격하게 감소하여 30일 지난 뒤에는 SST의 영향이 크게 미친다는 선행연구와 일치한다(Chen et al., 2010). 위도에 따라 각 초기조건들이 미치는 영향을 보기 위하여 Figs. 6e와 7e에 TCC 동서평균값(0^o~360^oE)을 나타냈다. 위도에 따라서 지면과 해양 초기장의 영향에 따른 계절 예측 성능이 조금씩 달랐는데, T2m의 경우 적도와 저위도(30^oS~30^oN)에서 자료동화에 따른 계절 예측성능 증가가 크게 나타났으며 고위도(60^oN 이상)에서는 자료동화로 인한 예측 성능 증가가 크게 나타나지 않았다. 오히려 고위도 북반구의 경우 AMIP과 noDA 초기조건을 사용한 EXP3 실험이 다른 실험들에 비하여 높은 TCC를 보였다. SST의 경우 적도 및 저위도에서는 T2m와 유사한 결과를 보이지만, 고위도에서는 T2m와 달리 4개의 모든 실험 결과들이 큰 차이 없이 유사하게 나타났다.

Fig. 5.

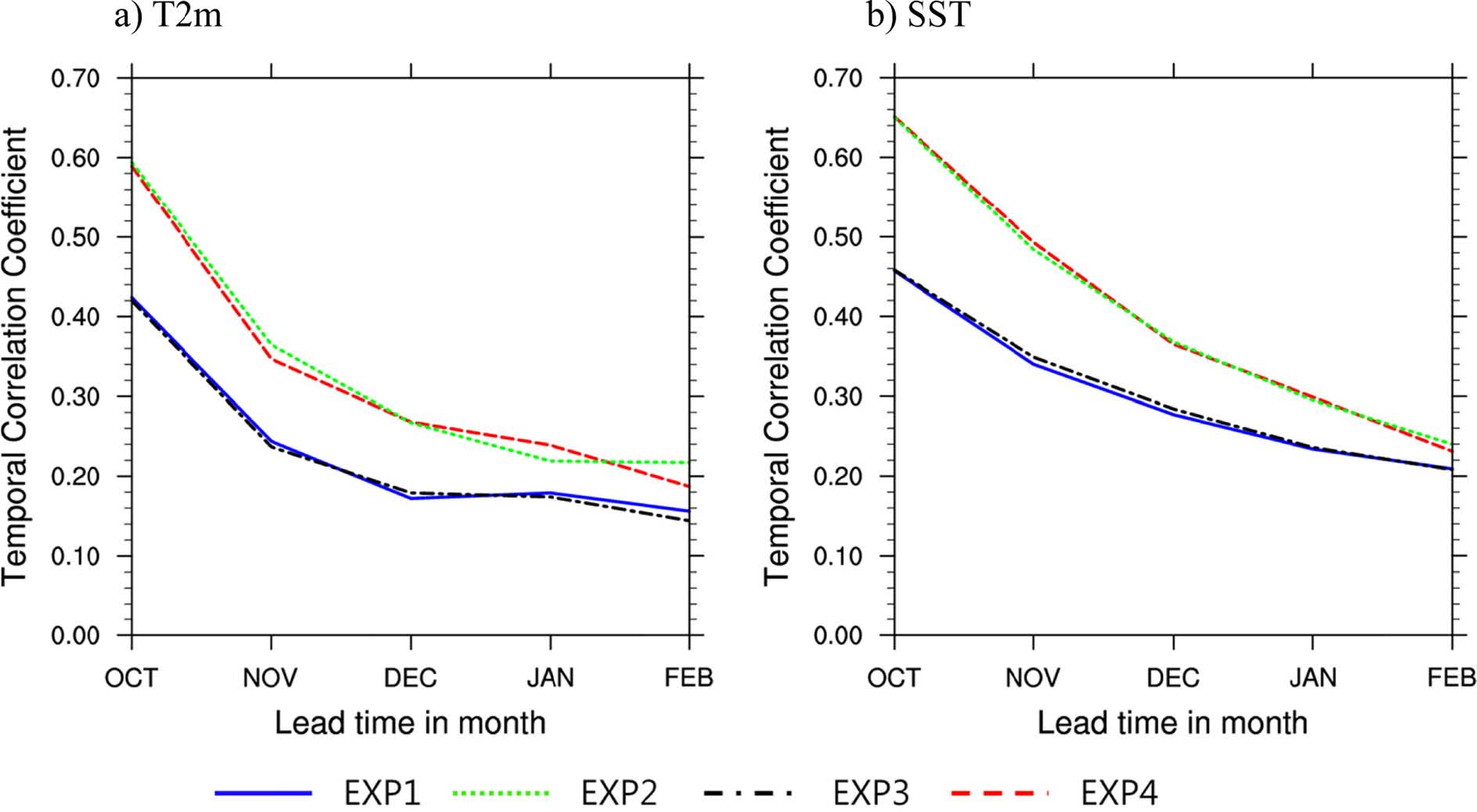
Global mean temporal correlation coefficient for T2m and SST with respect to lead time (month). The blue, green, black and red lines denote EXP1, EXP2, EXP3 and EXP4 respectively.

Fig. 6.

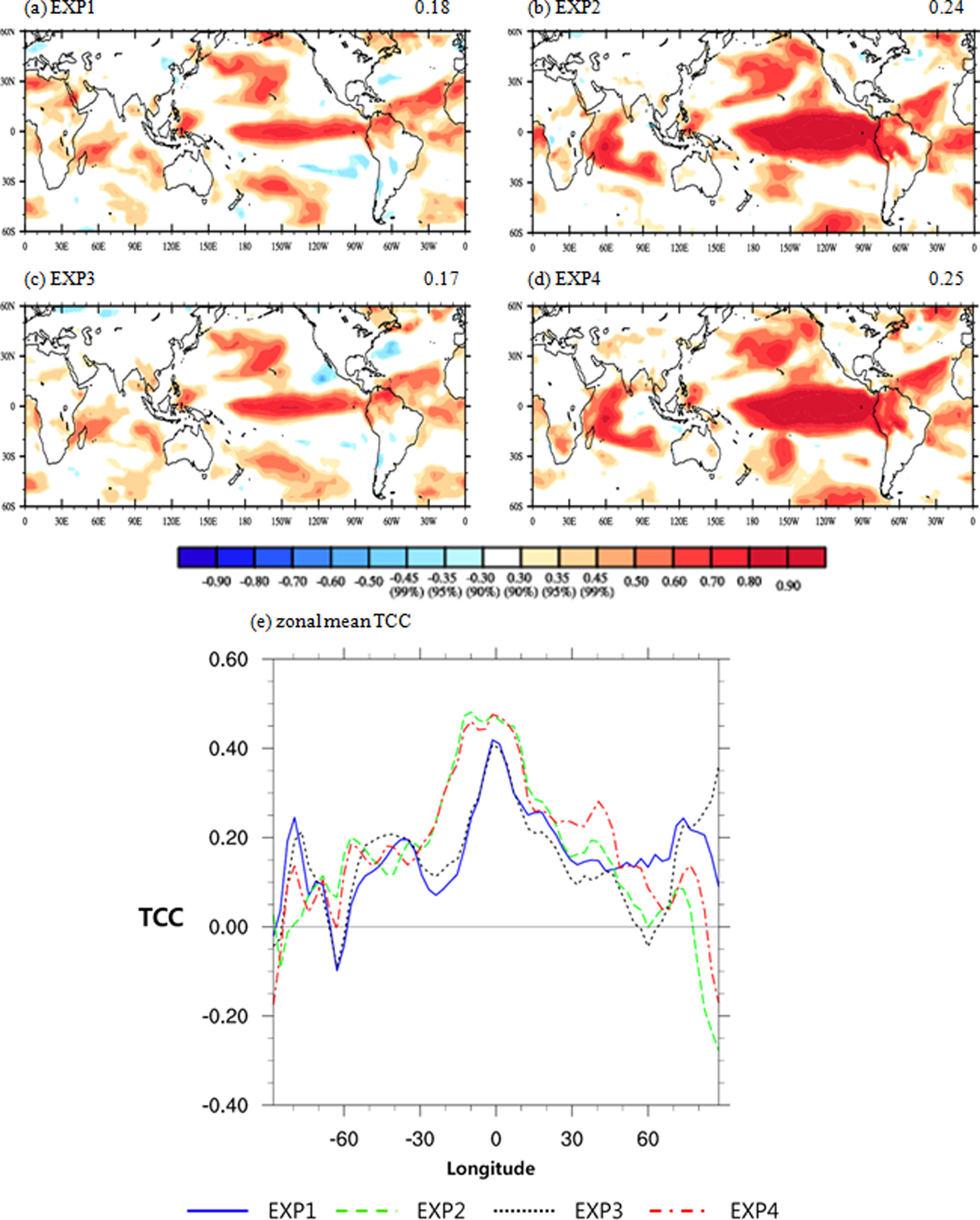
Temporal correlation coefficients map (a~d) and zonal mean TCC (e) (0o~360oE) of T2m between observation and each experiments for boreal winter (DJF, lead2-4). The values at the top left of each figure (a~d) are the global mean TCC. The blue, green, black and red lines denote EXP1, EXP2, EXP3 and EXP4 respectively.

Fig. 7.

Same as in Fig. 6, but for SST.

Fig. 8.

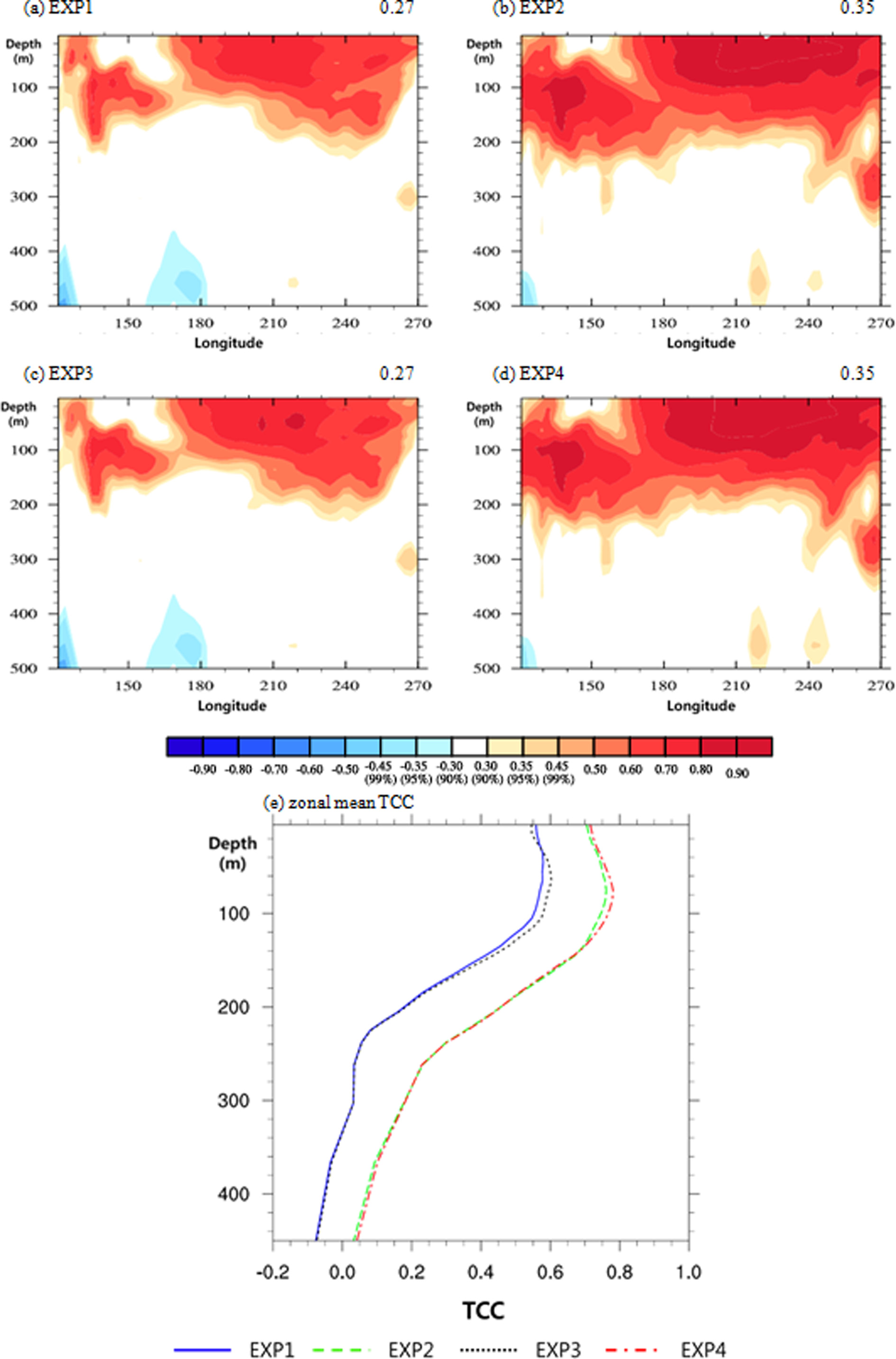
Same as in Fig. 7, but for vertical cross sections and zonal mean (120o~270oE) of potential sea temperature for the section from 5oS to 5oN.

Fig. 9.

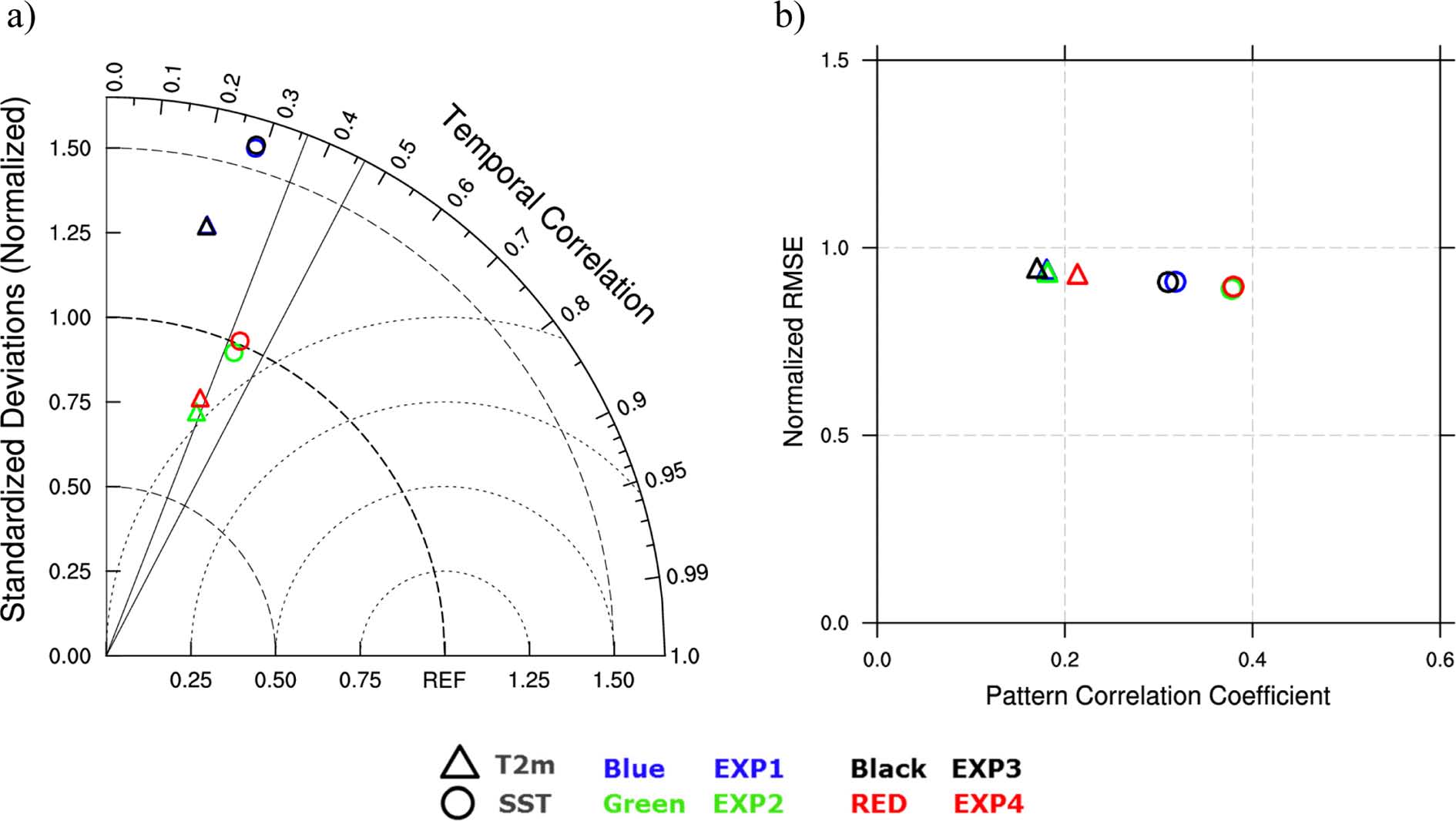
a) Taylor diagram and b) PCC-RMSE scatter plot of T2m (triangle) and SST (circle) for boreal winter (DJF, lead2-4) from 50oS to 50oN. The blue, green, black and red colors denote EXP1, EXP2, EXP3 and EXP4 respectively.

해수면 외에도 해양의 하층을 살펴보기 위하여, Fig. 8에서 각 층에 대한 북반구 겨울철(DJF) 해수온도의 TCC를 살펴 보았다. 이 그림은 위도방향으로 평균(5^oS~5^oN) 된 그림으로, 적도 태평양의 예측성을 연직구조로 나타내었다. 이 지역은 Hadley circulation의 upward branch이자, ENSO 현상이 나타나는 곳으로 지구 전체 대기 순환에 영향을 미치는 중요한 지역이다. 자료동화가 적용되지 않은 실험들(EXP1, EXP3)은 적도 동태평양이 0~200 m까지 재분석 자료와 높은 예측성을 보임에도 불구하고 서태평양에는 낮은 예측성을 보인다. 반면 자료동화가 적용된 실험들(EXP2, EXP4)은 동태평양 지역뿐만 아니라 서태평양 지역에서도 0~200 m까지 재분석 자료와 매우 높은 상관성을 보이고 있다. 특히 100~200 m 사이에서 자료동화를 적용함에 따라 예측성 향상이 크게 나타났다. 각 실험별 수심에 따른 해수온도의 TCC를 보기 위하여 Fig. 8e에 동서평균값(120^o~270^oE)을 수심에 대하여 나타내었다. 모든 실험에서 해수면에서 약 100아래 까지는 TCC가 증가하다가, 그 뒤로는 감소하는 형태를 보인다. 초기조건에 따른 영향을 살펴보면 해수면 분석과 마찬가지로, 자료동화에 따라 계절 예측성 향상이 크게 나타났으며, AMI와 CMI 등 지면 초기조건의 영향은 해수면 근처에서 약간의 차이가 있을 뿐 하층으로 내려갈수록 그 차이는 거의 나타나지 않았다.

Figure 9의 경우 북반구 겨울철(DJF) T2m(세모)와 SST(원)의 Taylor diagram과 Pattern correlation coefficient (PCC)와 Root Mean Square Error (RMSE)의 scatter plot을 나타내었다. 파란색, 녹색, 검정색, 빨간색은 순서대로 EXP1, EXP2, EXP3, EXP4의 결과이다. 여기서 나타내는 값들(TCC, RMSE, PCC, normalized standard deviation (NSTD))은 각각 0^o~360^oE, 50^oS~50^oN에 해당하는 영역에 대하여 면적평균된 값이다. Taylor diagram은 NSTD과 TCC를 함께 나타낸 그림으로, NSTD는 모형의 변동성에서 관측의 변동성을 나눈 것으로 REF (1)에 가까울수록 관측과 변동성이 같음을 의미한다. PCC의 경우 재분석 자료와의 공간적 상관성을 나타내는 것으로 1에 가까울수록 재분석 자료와 유사함을 의미하며, RMSE는 재분석 자료와의 차이를 나타내는 값으로 0에 가까울수록 재분석 자료와 유사하다. NSTD의 경우 자료동화를 적용하지 않은 초기조건을 사용한 결과에서는 재분석자료에 비해 높은 변동성을 보였지만, 자료동화를 적용한 초기조건을 사용한 실험은 재분석 자료와 유사한 변동성을 보였다. 그뿐만이 아니라 자료동화가 적용된 초기조건을 사용한 실험들(EXP2, EXP4)은 그렇지 않은 실험들(EXP1, EXP3)에 비해 TCC와 PCC는 증가되었으며, RMSE는 감소하였다. 특히 PCC의 경우 같은 자료동화를 사용한 결과임에도 불구하고 T2m에서 지면 초기조건에 따라 EXP4 실험이 EXP2 실험보다 높은 값을 보였다. 하지만 SST에서는 이러한 차이가 보이진 않았다. T2m의 PCC를 제외하고 AMI와 CMI를 비교할 경우 지면 초기조건이 계절 예측에 미치는 영향은 해양 자료동화의 효과에 비해 크게 나타나지 않았다.

4. 요약 및 결론

본 연구에서는 접합대순환모형의 지면과 해양 초기조건의 생산방법에 따라 계절 예측성에 미치는 효과를 살펴 보았다. 지면 초기장의 경우 AMIP-type 적분을 통해 연속적으로 지면 정보를 생산하여 초기조건내에 있는 모든 지면층 간에 연속성 및 일관성을 유지하도록 한 후, 만들어진 AMIP-type 적분 결과를 직접적으로 사용할 때와 기후값을 사용할 때로 분류하였다. 해양 초기장의 경우 관측과 자료동화기법(DA)을 이용하여 모든 수심에서 관측과 시공간적 패턴이 유사하도록 만든 초기조건과 자료동화가 적용되지 않은 초기조건으로 분류하였다. 초기조건에 따른 예측성을 비교하기 위해 사용한 접합대순환모형은 PNU CGCM이다. 자료의 기간은 32년이며(1980~2011), 매해 10월에 적분을 시작하였다. 여기서 lead time (month)은 5개월(October to February)이고, 분석변수는 T2m, SST이다. 두 변수 모두 자료동화가 적용된 초기조건을 사용한 실험(EXP2, EXP4)이 자료동화가 적용되지 않은 초기조건을 사용한 실험(EXP1, EXP3)보다 TCC의 영역평균(0^o~360^oE, 60^oS~60^oN)값이 북반구 겨울철(DJF)에 대하여 향상됨을 보였다. 특히 공간적으로는 적도 태평양에서 TCC의 향상이 크게 나타났다. 반면 AMI과 CMI과 같이 지면 초기조건에 따른 실험들간에 예측성 차이는 크게 나타나지 않았다. 해수온도를 연직적으로 살펴보면 자료동화가 적용된 초기조건을 사용한 실험(EXP2, EXP4)은 noDA 실험(EXP1, EXP3)에 비해 0~200 m까지의 적도 동태평양 부근의 예측성이 개선된 것으로 나타났다. NSTD와 TCC를 나타내는 Taylor diagram와 PCC-RMSE scatter plot를 분석해 본 결과 자료동화를 적용한 초기조건을 사용한 실험(EXP2, EXP4)이 그렇지 않은 실험(EXP1, EXP3)에 비해 높은 예측성을 보였으며, 지면 초기조건에 따라서는 예측성의 차이가 크게 나타나지 않았다.

해양 자료동화와 AMIP-type 지면초기자료가 계절 예측성에 미치는 영향을 종합해 보면, 대부분의 영향은 지면의 초기조건 변화보다는 자료동화로 인한 해양 초기조건 개선에서 오는 영향이 지배적임을 알 수 있었다. 하지만 본 연구에서 사용된 지면 초기조건은 AMIP-type 적분을 통해 생산된 반면 해양 초기조건의 경우 재분석 자료를 이용해 초기화되었기 때문에, 재분석 자료로 초기화된 해양 초기조건과 AMIP-type 적분으로 생성된 지면 초기조건이 미치는 계절 예측성을 동등하게 비교하기엔 한계가 있다. 위도별로 초기조건에 따른 예측성능의 향상 정도가 다르게 나타났는데, 적도를 포함한 저위도 지역에서는 자료동화에 따른 예측성 향상이 크게 나타나는 반면, 고위도에서는 그 영향이 크게 나타나지 않았다. 위도에 따른 예측성 향상 차이는 많은 요인이 있겠지만 그 중 하나는 자료동화에서 사용된 재분석 자료(GODAS)가 위도 74.5^oS~64.5^oN 영역으로 제한적이기 때문이다. 즉, 재분석으로 인해 자료동화가 수행된 초기조건영역은 74.5^oS~64.5^oN이기 때문에 그 이상의 고도에서는 계절 예측성 증가 효과가 크게 나타나지 않은 것으로 보인다. 지면초기조건에 따른 계절 예측성은 4개의 실험 모두에서 차이가 작게 나타났지만, 자료동화를 사용한 해양 초기조건과 AMI 지면 초기조건으로 실험된 EXP4 결과가 가장 좋은 북반구 겨울철 예측 성능을 보였다.

Acknowledgments

이 논문은 부산대학교 자유과제 학술연구비(2년)에 의해서 연구되었습니다.

REFERENCES

• Ahn, J. B., and J. A. Lee, (2011), Numerical study on the role of sea-ice using ocean gerneral cirulation model, J. Korean Soc. Oceanogr, 6, p225-233.
• Ahn, J. B., J. L. Lee, and E. S. Im, (2012(a)), The reproducibility of surface air temperature over South Korea using dynamical downscaling and statistical correction, J. Meteor. Soc. Japan, 90, p493-507. [https://doi.org/10.2151/jmsj.2012-404]
• Ahn, J. B., S. B. Lee, and S. B. Ryoo, (2012(b)), Development of 12-month ensemble prediction system using PNU CGCM V1.1, Atmos. Korean Meteor. Soc., 22, p455-464. [https://doi.org/10.14191/atmos.2012.22.4.455]
• Ahn, J. B., Y. H. Yoon, E. H. Cho, and H. R. Oh, (2005), A study of global ocean data assimilation using VAF, J. Korean. Soc. Oceanogr., 10, p69-78.
• Alves, O., M. A. Balmaseda, D. Anderson, and T. Stockdale, (2004), Sensitivity of dynamical seasonal forecasts to ocean initial conditions, Quart. J. Roy. Meteor. Soc., 130, p647-667. [https://doi.org/10.1256/qj.03.25]
• Anderson, J. L., and J. J. Ploshay, (2000), Impact of initial conditions on seasonal simulations with an atmospheric general circulation model, Quart. J. Roy. Meteor. Soc., 126, p2241-2264. [https://doi.org/10.1002/qj.49712656713]
• Balmaseda, M., and D. Anderson, (2009), Impact of initialization strategies and observations on seasonal forecast skill, Geophys. Res. Lett., 36, pL01701. [https://doi.org/10.1029/2008GL035561]
• Behringer, D. W., M. Ji, and A. Leetmaa, (1998), An improved coupled model for ENSO prediction and implications for ocean initialization. Part I: The ocean data assimilation system, Mon. Wea., Rev., 126, p1013-1021. [https://doi.org/10.1175/1520-0493(1998)126<1013:aicmfe>2.0.co;2]
• Bennett, A. F., (2002), Inverse modeling of the ocean and atmosphere, Cambridge University Press. [https://doi.org/10.1017/CBO9780511535895]
• Bonan, G. B., (1998), The land surface climatology of the NCAR Land Surface Model (LSM 1.0) coupled to the NCAR Community Climate Model (CCM3), J. Climate, 11, p1307-1326. [https://doi.org/10.1175/1520-0442(1998)011<1307:TLSCOT>2.0.CO;2]
• Branković, Č., T. N. Palmer, F. Molteni, S. Tibaldi, and U. Cubasch, (1990), Extended?range predictions with ECMWF models: Time?lagged ensemble forecasting, Quart. J. Roy. Meteor. Soc., 116, p867-912. [https://doi.org/10.1002/qj.49711649405]
• Charney, J. G., (1951), Dynamical forecasting by numerical process, Compendium of Meteorology, T. F. Malone Ed., Amer. Meteor. Soc., p470-482.
• Chen, M., W. Wang, and A. Kumar, (2010), Prediction of monthly-mean temperature: The roles of atmospheric and land initial conditions and sea surface temperature, J. Climate, 23, p717-725. [https://doi.org/10.1175/2009JCLI3090.1]
• Collins, M., S. F. B. Tett, and C. Cooper, (2001), The internal climate variability of HadCM3, a version of the Hadley Centre coupled model without flux adjustments, Clim. Dynam., 17, p61-81. [https://doi.org/10.1007/s003820000094]
• Dommenget, D., and D. Stammer, (2004), Assessing ENSO simulations and predictions using adjoint ocean state estimation, J. Climate, 17, p4301-4315. [https://doi.org/10.1175/3211.1]
• Gates, W. L., (1992), AMIP: The atmospheric model intercomparison project, Bull. Amer. Meteor. Soc., 73, p1962-1970. [https://doi.org/10.1175/1520-0477(1992)073<1962:ATAMIP>2.0.CO;2]
• Ghil, M., and P. Malanotte-Rizzoli, (1991), Data assimilation in meteorology and oceanography, Adv. Geophys., 33, p141-266. [https://doi.org/10.1016/S0065-2687(08)60442-2]
• Gregory, D., and Coauthors , (2000), Revision of convection, radiation and cloud schemes in the ECMWF Integrated Forecasting System, Quart. J. Roy. Meteor. Soc., 126, p1685-1710. [https://doi.org/10.1002/qj.49712656607]
• Guilyardi, E., and Coauthors , (2004), Representing El Niño in coupled ocean-atmosphere GCMs: the dominant role of the atmospheric component, J. Climate, 17, p4623-4629. [https://doi.org/10.1175/JCLI-3260.1]
• Hendon, H. H., M. C. Wheeler, and C. Zhang, (2007), Seasonal dependence of the MJO-ENSO relationship, J. Climate, 20, p531-543. [https://doi.org/10.1175/JCLI4003.1]
• Houtekamer, P. L., and J. Derome, (1995), Methods for ensemble prediction, Mon. Wea. Rev., 123, p2181-2196. [https://doi.org/10.1175/1520-0493(1995)123<2181:MFEP>2.0.CO;2]
• Huang, X. Y., (2000), Variational analysis using spatial filters, Mon. Wea. Rev., 128, p2588-2600. [https://doi.org/10.1175/1520-0493(2000)128<2588:VAUSF>2.0.CO;2]
• Hurrel, J., J. J. Hack, B. A. Boville, D. Williamson, and J. T. Kiehl, (1998), The dynamical simulation of the NCAR Community Climate Model version 3 (CCM3), J. Climate, 11, p1207-1236. [https://doi.org/10.1175/1520-0442(1998)011<1207:TDSOTN>2.0.CO;2]
• IPCC, (1990), Climate Change: The IPCC Scientific Assessment Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge.
• IPCC, (2007), Climate Change 2007 - The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, [ Solomon, S., D. Qin, M. Manning, Z. Chen, M. Marquis, K. B Averyt, M. Tignor, and H. L Miller (eds.), [ Cambridge University Press, Cambridge, United?Kingdomand New York, NY, USA, p634p647p793-795.
• Ji, M., D. W. Behringer, and A. Leetmaa, (1998), An improved coupled model for ENSO prediction and implications for ocean initialization. Part II : The coupled model, Mon. Wea. Rev., 126, p1022-1034. [https://doi.org/10.1175/1520-0493(1998)126<1022:aicmfe>2.0.co;2]
• Kanamitsu, M., W. Ebisuzaki, J. Woollen, S. K. Yang, J. J. Hnilo, M. Fiorino, and G. L. Potter, (2002), NCEPDEO AMIP-II Reanalysis (R-2), Bull. Amer. Meteor. Soc., 83, p1631-1643. [https://doi.org/10.1175/BAMS-83-11-1631]
• Kessler, W. S., and R. Kleeman, (2000), Rectification of the Madden-Julian oscillation into the ENSO cycle, J. Climate, 13, p3560-3575. [https://doi.org/10.1175/1520-0442(2000)013<3560:ROTMJO>2.0.CO;2]
• Kharin, V. V., F. W. Zwiers, and N. Gagnon, (2001), Skill of seasonal hindcasts as a function of the ensemble size, Clim. Dynam., 17, p835-843. [https://doi.org/10.1007/s003820100149]
• Kiehl, J. T., and P. R. Gent, (2004), The community climate system model, version 2, J. Climate, 17, p3666-3682. [https://doi.org/10.1175/1520-0442(2004)017<3666:TCCSMV>2.0.CO;2]
• Kiehl, J. T., J. J. Hack, G. B. Bonan, B. A. Boville, B. P. Briegleb, D. L. Williamson, and P. J. Rasch, (1996), Description of the NCAR Community Climate Model (CCM3), NCAR Tech. Note. NCAR/TN-420+STR, p152.
• Kim, H. M., P. J. Webster, and J. A. Curry, (2012), Seasonal prediction skill of ECMWF System 4 and NCEP CFSv2 retrospective forecast for the Northern Hemisphere Winter, Clim. Dynam., 39, p2957-2973. [https://doi.org/10.1007/s00382-012-1364-6]
• Koster, R. D., and Coauthors , (2010), Contribution of land surface initialization to subseasonal forecast skill: First results from a multi-model experiment, Geophys. Res. Lett., 37. [https://doi.org/10.1029/2009gl041677]
• Koster, R. D., and Coauthors , (2011), The second phase of the global land-atmosphere coupling experiment: soil moisture contributions to subseasonal forecast skill, J. Hydrometeor, 12, p805-822. [https://doi.org/10.1175/2011JHM1365.1]
• Lorenz, E. N., (1963), Deterministic nonperiodic flow, J. Atmos. Sci., 20, p130-148. [https://doi.org/10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2]
• Lu, C., H. Yuan, B. E. Schwartz, and S. G. Benjamin, (2007), Short-range numerical weather prediction using time-lagged ensembles, Wea. Forecasting, 22, p580-595. [https://doi.org/10.1175/WAF999.1]
• Molteni, F., and Coauthors , (2011), The new ECMWF seasonal forecast system (System 4), ECMWF Technical Memorandum 656.
• Pacanowski, R. C., and S. M. Griffies, (1998), MOM 3.0 Manual. NOAA/Geophysical Fluid Dynamics Laboratory, Princeton, USA 08542.
• Palmer, T., and Coauthors , (2004), Development of a European multimodel ensemble system for seasonal-tointerannual prediction (DEME-TER), Bull. Amer. Meteor. Soc., 85, p853-872. [https://doi.org/10.1175/BAMS-85-6-853]
• Rayner, N. A., D. E. Parker, E. B. Horton, C. K. Folland, L. V. Alexander, D. P. Rowell, E. C. Kent, and A. Kaplan, (2003), Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century, J. Geophys. Res., 108(D14), p4407. [https://doi.org/10.1029/2002jd002670]
• Reichler, T. J., and J. O. Roads, (1999), The role of boundary and initial conditions for dynamical seasonal predictability, Nonlinear Proc. Geophys., 10, p211-232. [https://doi.org/10.5194/npg-10-211-2003]
• Saha, S., and Coauthors , (2006), The NCEP Climate Forecast Sys-tem, J. Climate, 19, p3483-3517. [https://doi.org/10.1175/JCLI3812.1]
• Saha, S., and Coauthors , (2010), The NCEP Climate Forecast System Reanalysis, Bull. Amer. Meteor. Soc., 91, p1015-1057. [https://doi.org/10.1175/2010BAMS3001.1]
• Saha, S., and and Coauthors , (2014), The NCEP climate forecast system version 2, J Climate, 27, p2185-2208. [https://doi.org/10.1175/JCLI-D-12-00823.1]
• Shi, L., O. Alves, H. H. Hendon, G. Wang, and D. Anderson, (2009), The role of stochastic forcing in ensemble forecasts of the 1997/98 El Nino, J. Climate, 22, p2526-2540. [https://doi.org/10.1175/2008JCLI2469.1]
• Stensrud, D. J., H. E. Brooks, J. Dun, M. S. Tracton, and E. Rogers, (1999), Using ensembles for short-range forecasting, Mon. Wea. Rev., 127, p433-446. [https://doi.org/10.1175/1520-0493(1999)127<0433:UEFSRF>2.0.CO;2]
• Stensrud, D. J., J. W. Bao, and T. T. Warner, (2000), Using initial condition and model physics perturbations in shortrange ensemble simulations of mesoscale convective systems, Mon. Wea. Rev., 128, p2077-2107. [https://doi.org/10.1175/1520-0493(2000)128<2077:UICAMP>2.0.CO;2]
• Sun, J. Q., and J. B. Ahn, (2011), A GCM-based forecasting model for the landfall of tropical cyclones in China, Adv. Atmos. Sci., 28, p1049-1055. [https://doi.org/10.1007/s00376-011-0122-8]
• Sun, J., and J. B. Ahn, (2015), Dynamical seasonal predictability of the Arctic Oscillation using a CGCM, Int. J. Climatol., 35, p1342-1353. [https://doi.org/10.1002/joc.4060]
• Wang, B., J. Y. Lee, and I. S. Kang, (2009), Advance and prospectus of seasonal prediction: assessment of the APCC/CliPAS 14-model ensemble retrospective seasonal prediction (1980–2004), Clim. Dynam., 33, p93-117. [https://doi.org/10.1007/s00382-008-0460-0]
• Wang, G., R. Kleeman, N. Smith, and F. Tseitkin, (2001), The BMRC coupled general circulation model ENSO forecast system, Mon. Wea. Rev., 130, p975-991. [https://doi.org/10.1175/1520-0493(2002)130<0975:TBCGCM>2.0.CO;2]
• Wunsch, C., (1996), The Ocean Circulation Inverse Problem, Cambridge University Press. [https://doi.org/10.1017/CBO9780511629570]
• Wikle, C. K., and L. M. Berliner, (2007), A Bayesian tutorial for data assimilation, Physica D., 230, p1-16. [https://doi.org/10.1016/j.physd.2006.09.017]
• Yang, S. C., M. Corazza, A. Carrassi, E. Kalnay, and T. Miyoshi, (2009), Comparison of local ensemble transform Kalman filter, 3DVAR, and 4DVAR in a quasigeostrophic model, Mon. Wea. Rev., 137, p693-709. [https://doi.org/10.1175/2008MWR2396.1]