GloSea5 모형의 6개월 장기 기후 예측성 검증

1. 서 론

계절 규모에서 기후예측성에 대한 연구는 과거 다양하게 진행되었다. 그러나 계절 규모 이상의 중장기 기후 예측성에 대한 연구는 상대적으로 미비한 형편이다(Van Oldenborgh et al., 2012). 최근 중장기 기후 변동성에 대한 연구가 활발히 이루어져 모델을 기반으로 한 중장기 계절예측시스템 또한 주목을 받고 있다. 이러한 흐름에 맞춰 계절예측시스템의 계절 규모에 대한 예측 가능성을 시공간적으로 파악하고 정량화하는 것이 중요한 연구 주제로 떠오르고 있다(Hurrell et al., 2009; Kim et al., 2012).

동아시아에서는 지역기후에 직접적인 영향을 미치는 몬순에 대한 연구가 활발히 이루어졌다. 몬순의 예측성에 대한 연구도 다수 이루어졌는데 여름 및 겨울몬순은 계절규모 이상에서는 예측성이 크지 않은 것으로 알려졌다(Wang et al., 2012). 특히 강우의 경우 예측성이 1~2개월 이내에 사라지는 것으로 보고되었다. 그러나 대규모 순환장은 일부 장기 예측이 가능한 것으로 밝혀졌는데 여름철 몬순 지수는 최대 5개월 전에 정성적으로 예측이 가능하다고 보고되었다(Lee et al., 2011; Li et al., 2012).

지역규모의 기후 변동성은 주로 인근 지역에 직접적으로 영향을 끼치지만 경우에 따라서는 원격 상관을 통해 지리적으로 거리가 먼 곳에도 간접적으로 영향을 미칠 수 있다. 일례로, 엘니뇨-남방진동(El-Nino Southern Oscillation, ENSO)은 열대 및 아열대 지역뿐 아니라 중위도 지역의 계절 변동성에도 영향을 미친다. 따라서 ENSO의 예측성이 1~2년으로 향상된다면 이는 농업, 수문학, 에너지 분야 등 여러 분야에 큰 영향을 미칠 수 있다(Sarachick and Cane, 2010). 이와 같은 중요성으로 인해 ENSO의 예측성은 여러기후 모델을 통해 활발히 연구되어 왔다. 최신 모델의 경우 대부분의 모델은 ENSO를 6~9개월 이상 예측할 수 있는 것으로 보고되었다(Jin et al., 2008; Wang et al., 2009).

국제적으로 계절예측에 대한 연구가 활발히 이루어지고 그 중요성이 주목 받고 있는 현 시점에서 국내에서도 계절예측시스템의 개발 및 기후 인자의 정확한 예측을 위한 다양한 노력을 기울이고 있다. 그 일환으로 한국 기상청과 국립기상과학원은 계절 규모에서 한영 공동 기후예측시스템을 정착하고 현업으로 이용하기 위해 영국 기상청(U.K. Met office)과 협력해 왔다. 그 결과, 2010년부터 영국 기상청의 전지구대기-해양-해빙 결합모델(HadGEM3)을 기반으로 한계절예측 시스템 Global Seasonal Forecasting System version 4 (GloSea4)를 도입하고 구축하였다.

선행연구에 따르면 GloSea4의 ENSO 예측성은 6개월 이상이다(Kang et al., 2011; Maclachlan et al., 2014). 그리고 예측성이 봄철에 감소하는 ‘ENSO spring predictability barrier’가 나타난다. 또한 서태평양으로 전이되는 ENSO 아노말리가 과대 모의되는 경향(Maclachlan et al., 2014)을 보이는데 이는 계절예측시스템이나 결합모델에서 일반적으로 나타나는 오차현상으로 개선이 필요하다(Luo et al., 2005; Guilyardi et al., 2009). GloSea4는 전 버전인 GloSea3에 비해 열대태평양의 해수면 온도나 각 기후 지수 등에서 전반적으로 개선된 결과를 보여주지만 지역적으로 좀 더 나은 예측을 위해 물리과정을 개선하고 연직 해상도를 높이는 등 개선이 필요한 것으로 보고되었다(Alberto et al., 2011).

기상청은 향상된 계절 예보를 위해 2014년 하반기부터 한영 공동계절예측시스템 GloSea4에서 모델 물리과정과 수평분해능을 개선한 고해상도 기후모델인 GloSea5 (GloSea version 5)를 현업에 도입하였다. 본 연구는 최근 구축된 GloSea5의 6개월 과거기후 모의자료를 이용해 최신 계절예측시스템의 6개월간 기후 예측 능력을 평가하고자 한다. 분석은 재분석 자료와의 비교를 통해 진행하였으며 구체적으로 기후시스템의 계절별 변동성을 파악하는 데 중요한 역할을 하는 기후변동지수를 선택하여 그 예측성을 진단하였다. 우선 지표기온의 예측성을 살펴본 후 동아시아 기후에 직 · 간접적으로 영향을 미치는 ENSO와 Indian Ocean Dipole (IOD) 및 다양한 몬순 지수의 예측성을 평가하였다.

2. 자 료

본 연구에서 사용된 모형자료는 HadGEM3를 기반으로 한 계절예측 시스템인 GloSea5의 과거 기후 모의자료이다. HadGEM3는 Met Office Unified Model (UM)의 대기모델과 Nucleus for European Modeling of the Ocean (NEMO)의 해양모델 및 Los Alamos sea ice model (CICE)의 해빙모델, 그리고 Met Office Surface Exchange Scheme (MOSES)의 지면 모델 및 대기-해양 플럭스 교환을 위한 OASIS 커플러로 구성된다. GloSea5의 수평격자 해상도는 위도 0.56^o와 경도 0.83^o이며 85개의 연직층을 갖는다. 1996년 2월부터 2009년 12월까지 총 14년 동안 매달 1일, 9일, 17일, 25일의 초기장을 이용하여 6개월 동안 적분된 hindcast의 월평균 값들을 이용하였다. 초기장과 모형내의 불확실성을 고려하여 1~3개의 앙상블 멤버를 이용하였으며, 앙상블 평균에 사용된 자료는 영국 기상청의 분석방법(Maclachlan et al., 2014)을 기반으로 17일을 제외한 25, 1, 9일의 앙상블 멤버이다. 일례로 Table 1은 2월을 기준으로 앙상블 멤버 구성 방법을 보여준다. 즉 해당월의 자료는 1월 25일, 2월 1일, 그리고 2월 9일 초기화된 모형의 결과를 이용한다.

GloSea5의 예측성을 평가하기 위해 비교대상으로 재분석자료와 관측자료를 이용하였다. 월평균 ERAInterim (Dee et al., 2009)을 이용하였고 해수면기온 관측자료는 월평균 Extended Reconstructed Sea Surface Temperature Version3 (ERSSTv3b; Smith et al., 2008)를 이용하였다. 강수량은 월평균 Global Precipitation Climatology Project (GPCP; Adler et al., 2003)를 이용하였다. 분석에 사용된 모든 자료들은(모형과 재분석 및 관측자료) 해상도를 통일하기 위해 위경도 2.5^o로 선형 내삽하였다.

Table 2는 본 연구에서 사용된 주요 기후 지수들의 정의와 변수명을 나타낸다. 지표대기온도(Surface Air Temperature, SAT)를 이용하여 전지구평균 지표대기온도(Global mean SAT; 이하 GMSAT)와 동아시아 지역에서 평균된 지표대기온도(East Asia SAT; 이하 EASAT)의 예측성을 평가하였다. 또한 동아시아 기후 변동에 많은 영향을 미치는 주요 기후모드인 ENSO지수(보다 구체적으로 Nino3.4 지수)와 인도양 쌍극자지수(Indian Ocean Dipole; 이하 IOD 지수; Saji et al., 1999)를 모형의 Skin temperature (TS)를 이용하여 Table 2와 같이 정의하였다. 여름-겨울철 동아시아 몬순 및 극한기상현상과 관련 있는 것으로 알려진 북극진동 지수(Arctic Oscillation index; 이하 AO 지수; Li and Wang., 2003), 여름철 동아시아지역의 하층순환을 대표하는 북대서양 몬순 지수(Western North Pacific Monsoon index; 이하 여름몬순1 지수; Wang et al., 2001)와 동아시아 몬순 지수(East Asian Monsoon index; 이하 여름몬순2 지수; Ha et al., 2005), 겨울철 동아시아 몬순지수를 대표하는 시베리아 고기압지수(Siberian High index; 이하 겨울몬순1 지수; Panagiotopoulos et al., 2005)와 동아시아 겨울몬순 지수(East Asian Winter Monsoon Index; 이하 겨울몬순2 지수; Jhun et al., 2004) 등을 Table 2와 같이 정의하여 GloSea5의 예측성 검증을 위한 주요 기후지수로 사용하였다.

Table 1.

An example of ensemble mean construction for February prediction.

Table 2.

Climate indices used in this study.

3. 예측성 평가 방법

GloSea5의 6개월 예측성 평가를 위해 매달 총 3일 (25, 1, 9일)의 초기장으로 적분이 시작된 원시 자료를 앙상블 평균한 후 사용하였다. 각 날짜의 적분마다 1~3개의 앙상블 멤버가 존재하기 때문에 앙상블 평균 값은 최소 3개에서 최대 9개의 멤버로 구성된다. 앙상블 멤버의 수가 예측성에 미치는 민감도에 관한 분석을 추가적으로 수행하여 결론 및 토의에서 논의하였다. Table 1은 2월에 적분이 시작되는 hindcast의 앙상블 평균을 구하는 데 쓰인 자료의 구성을 나타낸 보기이다. Lead time(0~5)은 예측 시점과 초기화 시점의 시간상 차이(월 단위)로서 Lead time 0은 해당월의 초기장을 이용해 같은 달의 월 평균 값을 예측한 것이며, Lead time 5는 5개월 전 초기장을 이용하여 적분된 결과를 나타낸다. 즉 Lead time이 5인 7월의 예측성은 1월 25일, 2월 1일, 2월 9일의 초기장으로 적분을 시작한 앙상블 멤버들(3개에서 9개)을 이용한 앙상블 평균으로 평가되었다.

모델 결과는 적분 시간이 증가할수록 모델 내에 존재하는 climate drift (기후 모델들의 장기 적분에서 외부 강제력(external forcing) 없이도 나타나는 경향성; Gupta et al., 2012)가 나타나는데 이는 관측과의 오차를 일으키는 중요한 요인이다. 예측성 평가지수를 분석하기 전에, 이러한 모델의 구조적 오차를 제거하기 위해 각 월별로 관측 자료를 이용하여 보정해 주었으며 자세한 식은 아래와 같다(Meehl et al., 2014).

H_jτ는 각 초기장에 따른 앙상블 평균한 월별 모델 값을 의미한다. j는 대상이 되는 월에 대해 총 14년 동안 각 해에 해당하는 값(j = 1~14)이고 τ는 예측 시기와 초기된 시기의 차이, 즉 lead time (τ = 0~5)이다. O_jτ는 H_jτ에 상응하는 시기의 관측 값을 의미한다. H'_jτ는 위의 식을 바탕으로 구조적 오차를 제거한 후, 실제 본 연구에서 사용한 월별 값이다. $$ {\stackrel{-}{H}}_{\text{τ}}$$와 $$ {\stackrel{-}{O}}_{\text{τ}}$$는 각 lead time에 따른 전체 시기의 평균으로 아래와 같이 정의된다.

본 연구에서 n은 14 (1996년부터 2009년까지 총 14년)이다. 보정 식을 이용하면 원시 모델 값에서 각 lead time에서의 모델과 관측의 평균차이를 빼줌으로써 구조적 오차를 제거할 수 있으며, 이 과정을 모형 오차 수정(Bias correction)이라 한다.

Figure 1은 모형 오차 수정을 GloSea5에 적용하였을 때 모델 내의 drift가 얼마나 효과적으로 제거되었는지 보여준다. Figure 1의 파란색과 빨간색 실선은 각각 2월과 8월에 초기화된 자료와 관측의 차이로써 모형 오차 제거 전의 drift 현상(lead time이 증가함에 따라 예측 값이 음의 경향성을 보임)이 나타나는 것을 확인할 수 있다. 모형 오차 수정 후(하늘색과 주황색 실선) 이러한 경향성이 효과적으로 제거되었음을 확인할 수 있다. 따라서 본 연구에서 계산된 모델 자료는 모두 구조적 오차를 제거한 후 사용하였고, 이는 GloSea5가 갖는 climate drift가 예측성 평가에 미치는 영향을 최소화한 자료라고 할 수 있다.

재분석 및 관측 자료를 통해 보정된 자료의 예측성은 예측성 평가 인자인 이상상관계수(Anomaly Correlation Coefficient; ACC)와 평균제곱근 예측성(Mean Squared Skill Score; MSSS)을 이용해 평가하였다. 각 평가 인자는 다음과 같이 정의된다.

여기서 각 기호의 의미는 앞서 기술한 식에서 설명하였다. ACC는 관측과 모델이 가지는 선형 상관관계에 대한 예측성 진단 변수로 1에 가까울수록 관측의 변동성을 모델의 예측 값이 잘 모의하고 있음을 의미한다. MSSS는 평균제곱오차(Mean Squared Error; MSE)를 이용해 구할 수 있다.

위의 식을 정리하면 아래와 같이 표현할 수 있다.

MSSS는 US CLIVAR Decadal predictability Working Group으로부터 다년 시간규모의 예측성 평가를 위해 제안된 진단변수이며(Goddard et al., 2013), Choi et al. (2015)에서 1년 이하의 계절 규모 예측성 평가를 위해 사용된 바 있다. 위의 식처럼 MSSS는 ACC 및 예측과 관측의 분산비율(s_H/s_O)에 관한 함수라고 할 수 있다. 예측과 관측의 분산 비율이 고려된 괄호 안의 식 (ACC(τ) - (s(τ)_H/_s(τ)_O))을 조건부 오차(Conditional bias)라 한다. 즉, MSSS는 ACC와 조건부 오차(Conditional bias)의 값이 고려된 예측성 진단변수이다. 조건부 오차는 ‘평균 오차(mean bias)’와는 다른 개념으로 관측과 예측의 평균이 같더라도 시간에 따른 경향성의 크기가 다를 때 존재 할 수 있다. 이는 기존 ACC가 관측과 모형 간의 분산 차이를 고려하지 못하는 단점을 보완할 수 있으며 1에 가까울수록 모형의 예측성이 우수함을 뜻한다. 이 점에 있어 MSSS는 ACC보다 훨씬 정량적인 예측성 평가 지수라고 할 수 있다.

위와 같은 방법으로 평가된 예측성 진단변수는 적은 표본 수 때문에 통계적 유의성에 대한 평가가 반드시 필요하다. 본 연구에서는 Goddard et al. (2013)이 제안한 bootstrap기반의 방법을 사용하여 ACC와 MSSS가 ‘0’ 이상의 값을 몇 번 갖는지에 대한 통계적 유의성을 평가하였다. 통계적 유의성 평가를 위해 무작위로 앙상블 멤버를 선택해 앙상블 평균을 구하고, 여기서 중복을 허용하여 n개의 표본을 또다시 무작위로 선택한다. 이 표본을 이용하여 ACC 또는 MSSS를 계산하는데, 본 연구에서는 이 과정을 1,000번 반복하였다. ACC와 MSSS는 관측과 모델의 변동성을 반영하여 두 자료의 상관성을 표현하는 계수이므로 예측성 평가에서는 양의 값만이 유의미하다. 이 계수들이 음의 값을 갖는다는 것은 모델이 관측의 변동성을 반대로 모의한다는 것이며, 이는 모델의 예측이 반대로 되고 있음을 뜻한다. 따라서 무작위로 계산된 1,000개의 각 표본에서 음의 값이 나오는 횟수(m)를 계산하고, m/1,000을 p-value로 사용한다. 이 p-value의 값이 α보다 작을 때, (1 - α) × 100% 신뢰 수준에서 유의하다고 할 수 있다.

Fig. 1.

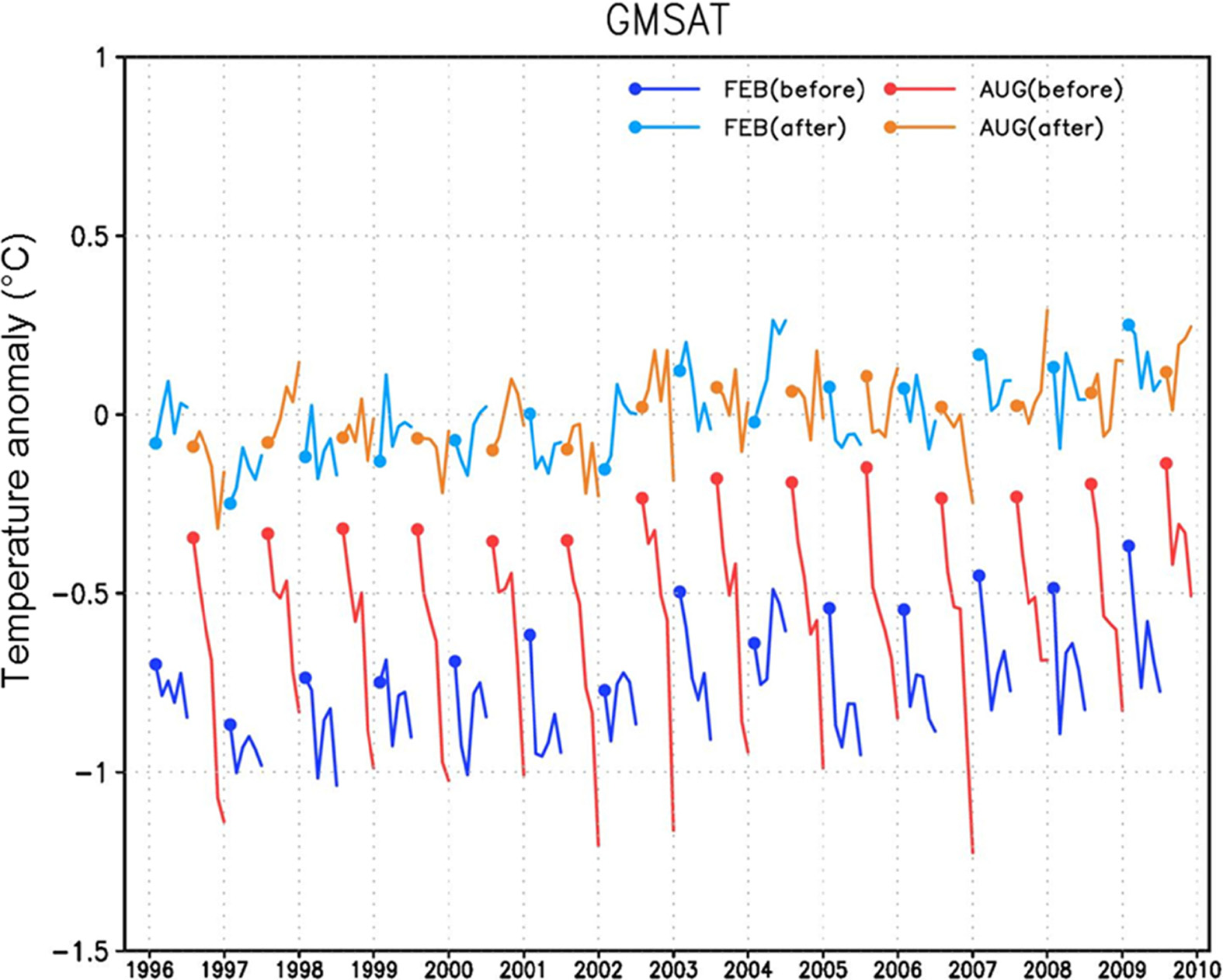
Time series of GMSAT for February and August prediction before (blue and red) and after (sky blue and orange) bias correction.

Fig. 2.

The ACC and MSSS of (a) GMSAT and (b) EASAT prediction. Initialized month is indicated by the first circle in each month. Filled (open) circle indicates the values that are statistically significant at the 95% (90%) confidence level.

4. 지표 대기 온도(SAT)의 예측성

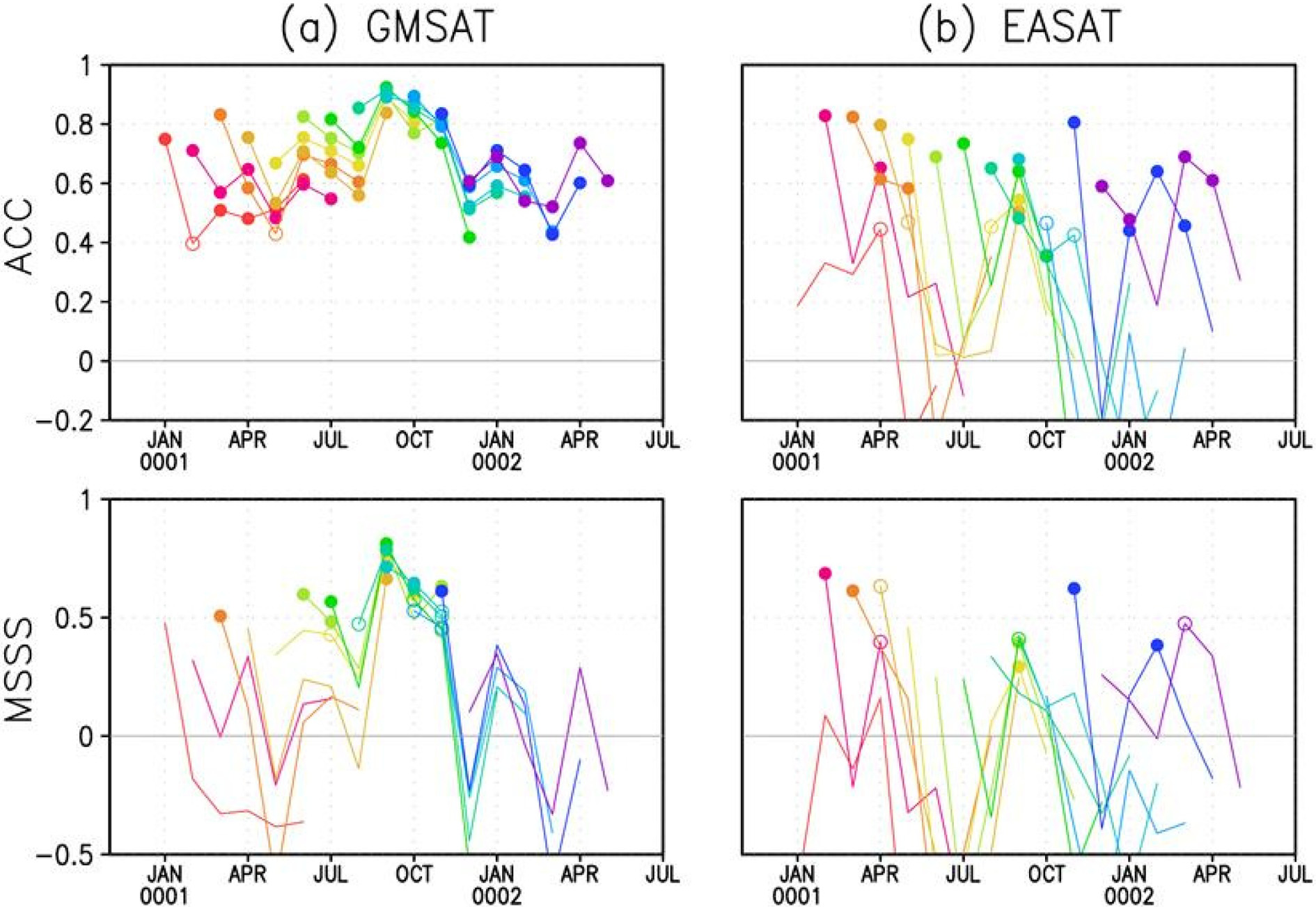
본 절에서는 SAT의 예측성을 평가하기 위해 전지구 평균과 동아시아 평균을 분석하였다. 전지구 평균된 지표대기온도(GMSAT)와 동아시아 평균된 지표온도(EASAT)의 월별 ACC와 MSSS를 Fig. 2에 나타냈다. 각 월에 해당하는 채워진 원(빈 원)은 예측성 진단변수가 통계적 95% (90%) 유의수준에서 신뢰할 수 있음을 의미한다. 빨간색과 보라색 실선은 각각 1월과 12월에 초기화된 hindcast의 예측성 진단변수의 결과이다. 각 실선들은 lead time 0에서 5까지의 결과를 나타내고 있다. 예를 들어 GMSAT의 ACC 결과를 보면, 보라색 실선에서 6개의 채워진 원이 의미하는 것은 12월에 초기화된 hindcast의 GMSAT 예측성이 lead time 0에서 5까지 95% 신뢰수준에서 모두 통계적으로 유의하다는 것을 뜻한다. GMSAT의 월별 예측성을 살펴보면 가을철에 높고 겨울철에 낮다. 또한 통계적으로 유의한 수준에서 여름에 시작된 예측이 겨울에 시작된 예측보다 오래 지속됨을 알 수 있다. MSSS로 평가된 GMSAT의 예측성은 ACC가 높게 나타났던 가을철만 통계적으로 유의하다. 즉, GMSAT의 정성적 예측은 6개월의 시간 규모에서 가능하나 조건부 오차를 고려한 보다 정량적인 예측은 2~3개월에 국한된다.

Fig. 3.

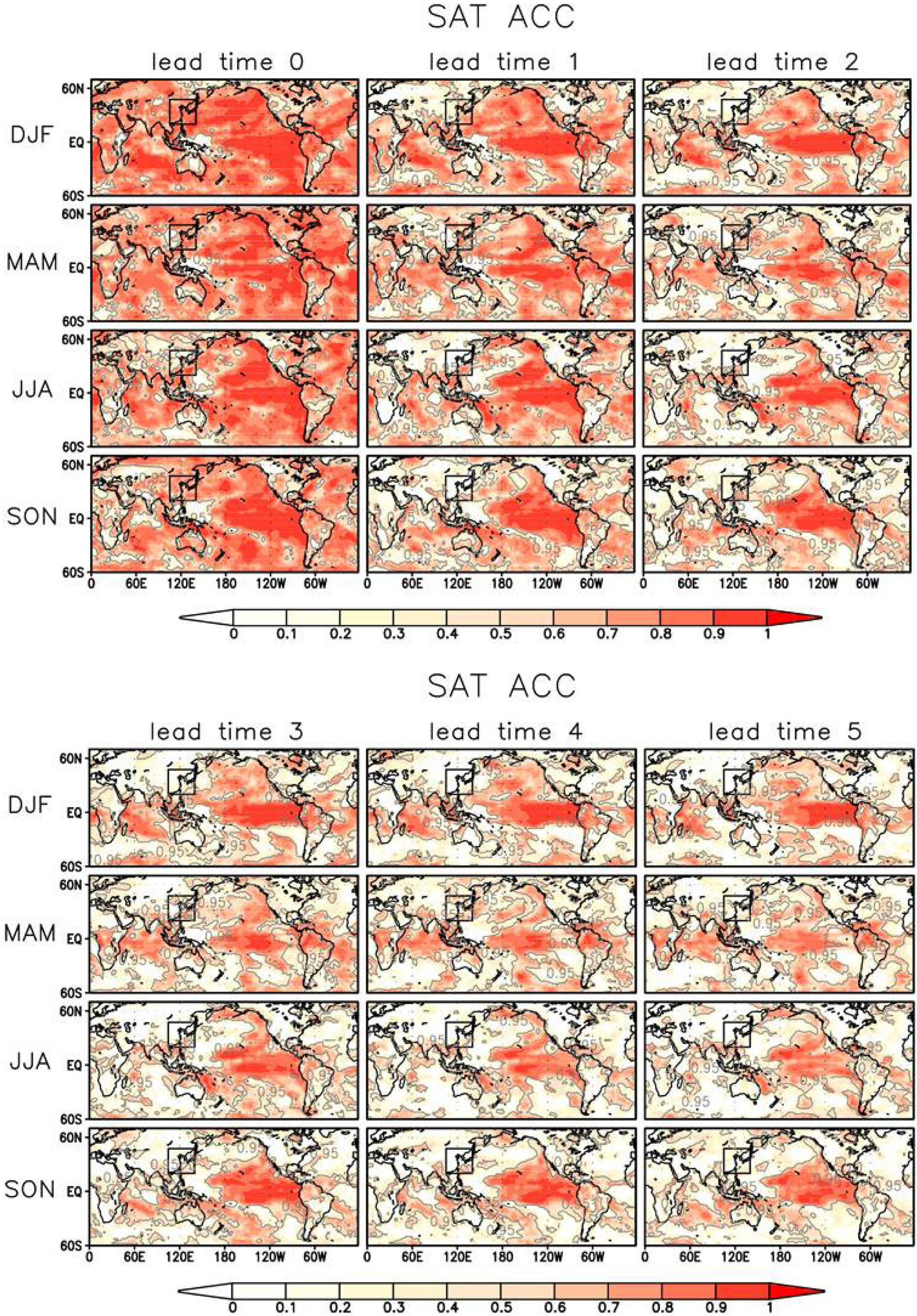
Spatial pattern of ACC for surface air temperature (SAT) at each season and lead time. A squared indicates geographical domain used to define East Asia. Gray lines indicate values that are statistically significant at the 95% confidence level.

동아시아 지역을 살펴본 EASAT의 ACC는 일부 계절만 약 2개월 정도 예측이 가능할 뿐 lead time 0을 제외하고는 통계적으로 유의하지 않다. ACC보다 예측성을 낮게 평가하는 MSSS에서는 앞서 말한 특징이 더 두드러지게 나타난다. 동아시아는 큰 계절변동성을 가지기 때문에 SAT 또한 큰 계절변동성을 가지고 시간에 따른 편차가 크다. 이러한 특성 때문에 다양한 기후 모델에서 동아시아는 예측성이 떨어지는 지역으로 알려져 있다(Wang et al., 2009; Lee et al., 2010). GloSea5 또한 EASAT의 큰 계절변동성을 잘 모의하지 못하며, 전 계절에 걸쳐 예측성이 낮은 것으로 평가된다.

계절별 SAT의 lead time에 따른 ACC의 공간분포를 Fig. 3에 나타내었다. 회색 선은 95% 신뢰수준에서 통계적으로 유의한 지역의 경계를 의미한다. 우선 lead time이 증가할수록 전반적인 ACC가 감소하지만, 지역에 따른 차이가 존재함을 볼 수 있다. 검은 사각형은 예측성 분석을 위하여 정의한 동아시아 지역을 나타낸다. 동아시아를 포함한 유라시아 대륙의 SAT예측성을 살펴보면 전 계절에서 lead time 0을 제외하고는 통계적으로 유의하지 않은 것을 확인할 수 있다. ACC는 남미대륙의 열대 지역을 제외한 대부분의 대륙에서 대체적으로 낮은 반면 해양에서는 높게 나타난다. 적도태평양은 전 계절에서 유사한 예측성을 보이고 있으며, 서태평양보다는 동태평양에서 높게 나타난다. 북태평양 SAT는 겨울철에 가장 높은 예측성을 보이며 통계적으로 유의한 예측성이 lead time 5까지 존재한다. 인도양의 SAT 또한 겨울철과 봄철에 lead time 5까지 예측 가능하다. 대서양의 예측성은 lead time 2부터 일부 남대서양을 제외하고는 예측성이 눈에 띄게 감소하는데 이는 APCC/CliPAS 모델을 다룬 선행연구의 결과와 일관성이 있다(Wang et al., 2009). 선행연구에 따르면 CMIP5 모형에서도 유라시아 대륙과 캐나다 북쪽 대륙의 변동성을 잘 모의하지 못하였는데 이는 모델에서 빙권과 고위도 지역의 메커니즘이 대기 변수와 잘 결합되지 않아 발생한 것으로 보인다(Outten et al., 2013). 또한 모델에 사용되는 지면온도와 해빙의 초기값은 관측의 제한으로 인해 해양의 초기값보다 덜 안정적이기 때문에 해양에 비해 고위도 육지에서 발생하는 모형의 오차가 큰 것으로 보인다.

계절적으로 살펴보면 겨울철의 ACC는 다른 계절에 비해 전반적으로 넓은 지역에서 높은 값을 보이며, 적도태평양 주변 지역의 SAT의 예측성은 가을철에 가장 높게 나타난다. 전지구 평균시 적도 지역의 격자값은 고위도 지역의 값보다 더 큰 비중으로 고려된다. 따라서 GMSAT의 예측성이 가을철에 높게 나타난 것(Fig. 2)은 이 계절에서 적도 태평양의 예측성 또한 높았기 때문이라고 볼 수 있다.

5. 해수면 온도(SST)의 예측성

해수면 온도의 예측성은 대표적인 경년 변동인 ENSO와 IOD 지수를 이용하여 살펴보았다. ENSO는 적도 부근의 해양과 대기의 상호작용으로 인해 일어나는 기후 경년 변동성으로 직접적으로는 적도태평양의 기압과 바람 및 강수에 영향을 주어 열대지역의 대류운동을 변동시킨다(Horel and Wallace, 1981). 엘니뇨 영향은 적도에 국한되지 않고, 발생 기간 동안 지구의 평균 기온을 높이며 워커 순환, 몬순의 강도, 태풍 주요 발생시점의 변화, 열대지역의 가뭄 등 열대 및 아열대 지역의 기후시스템에 변화를 일으킨다. 또한 원격상관을 통해 지리적으로 거리가 있는 중위도 지역(동아시아 및 한반도 등)의 계절 패턴에도 영향을 미치는 것으로 알려져 있으며 한반도의 온도와 강수 아노말리에도 영향을 준다는 선행연구들이 있다(Kang, 1998; Cha et al., 1999). 따라서 ENSO의 예측성은 동아시아 기후 예측성과 밀접한 관련이 있다.

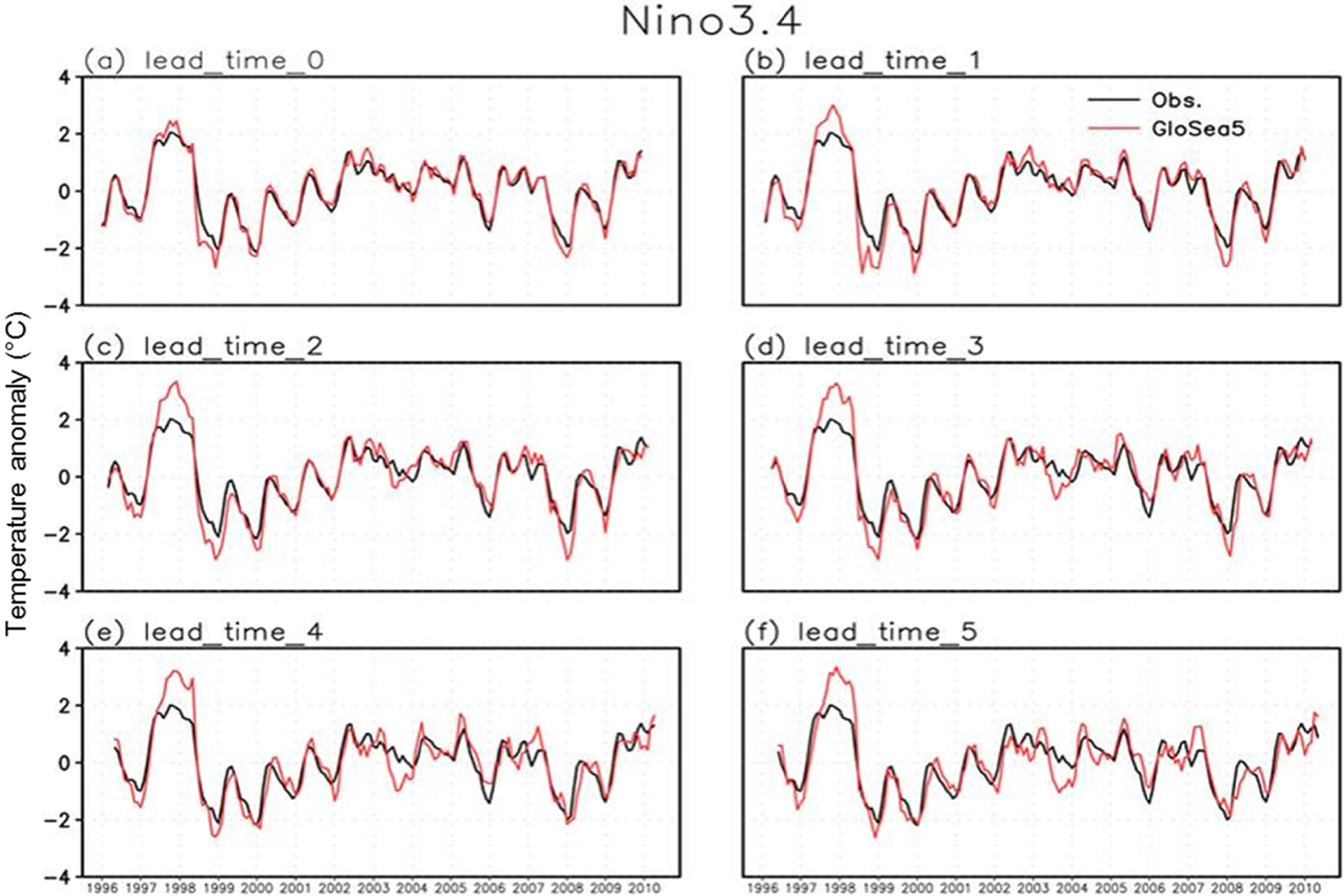
ENSO의 예측성은 Nino3.4 지수를 이용하여 진단하였다. Figure 4는 lead time에 따른 GloSea5의 hindcast(빨간색 실선)와 각 시기에 해당하는 관측 자료(검정색 실선, ERSSTv3)의 시계열이다. 역사상 가장 큰 엘니뇨였던 1997/98의 경우 모든 lead time에서 잘 모의되는데, lead time이 증가할수록 과대모의하는 경향이 있다. 바로 다음해에 발생한 1998/99와 1999/00의 라니냐도 잘 모의한다. 2000년 이후 발생한 다소 작은 크기의 엘니뇨들은 lead time 2까지 관측과 매우 유사하게 모의되고 있다.

선행연구에 의하면 다양한 기후 모델에서 ENSO의 예측성은 최소 6개월에서 2년까지 통계적으로 유의한 값을 가진다(Jin et al., 2008; Luo et al., 2008). Figure 5a는 Nino3.4의 예측성을 ACC와 MSSS로 정량적으로 평가한 결과이다. ENSO의 변동성이 큰 계절만을 고려하기 위해 관측 값을 사용한 Nino3.4 지수의 월별 표준편차를 구하여 변동성이 큰 6개월(Nino3.4 지수의 경우 9월에서 2월까지)을 선택하였고, Fig. 5에서 이를 제외한 계절은 회색으로 명암을 주었다. Nino3.4 지수의 ACC는 초기화된 월에 상관없이 0.7이상의 통계적으로 유의한 값을 가지며 특히 가을철, 겨울철에 높게 나타났다. MSSS의 결과도 일부 봄철을 제외하고 모두 통계적으로 유의한 예측성이 있는 것으로 나타났다. 가을철 Nino3.4의 높은 예측성은 GMSAT의 예측성을 높이는 데 일부 기여했다고 볼 수 있다(Fig. 2와 Fig. 5a 비교). Nino3.4 지수의 ACC는 lead time이 커질수록 대체적으로 감소하는 것을 알 수 있으며, 특히 봄철의 예측성 감소가 뚜렷하다. 예측성이 낮은 봄철은 초기화 월에 따른 퍼짐 정도가 크게 나타난다. ACC와 MSSS 모두 봄철에 가장 감소하는데, 이는 잘 알려진 ‘ENSO spring predictability barrier’ 현상이다. 이는 중-동태평양 지역의 SST에서 대기-해양 상호작용에 따른 1년 주기의 계절 변동이 강하게 나타나는데, 다른 계절에 비해 높은 봄철 SST의 평균 온도로 인해 오차의 성장률이 커져서 발생한다. 또한 ENSO의 성장률이 봄철에 가장 크기 때문에 그 자체의 변동성으로 인해 오차가 성장하는 원인도 있다(Moore and Kleeman, 2006). 종합적으로 GloSea5의 ENSO 예측성은 ENSO predictability barrier와 관련하여 봄철에 떨어졌다가, 이후에 다시 회복하는 경향을 보인다.

Fig. 4.

Time series of Nino3.4 index at each lead time from GloSea5 (red) and observation (black).

Fig. 5.

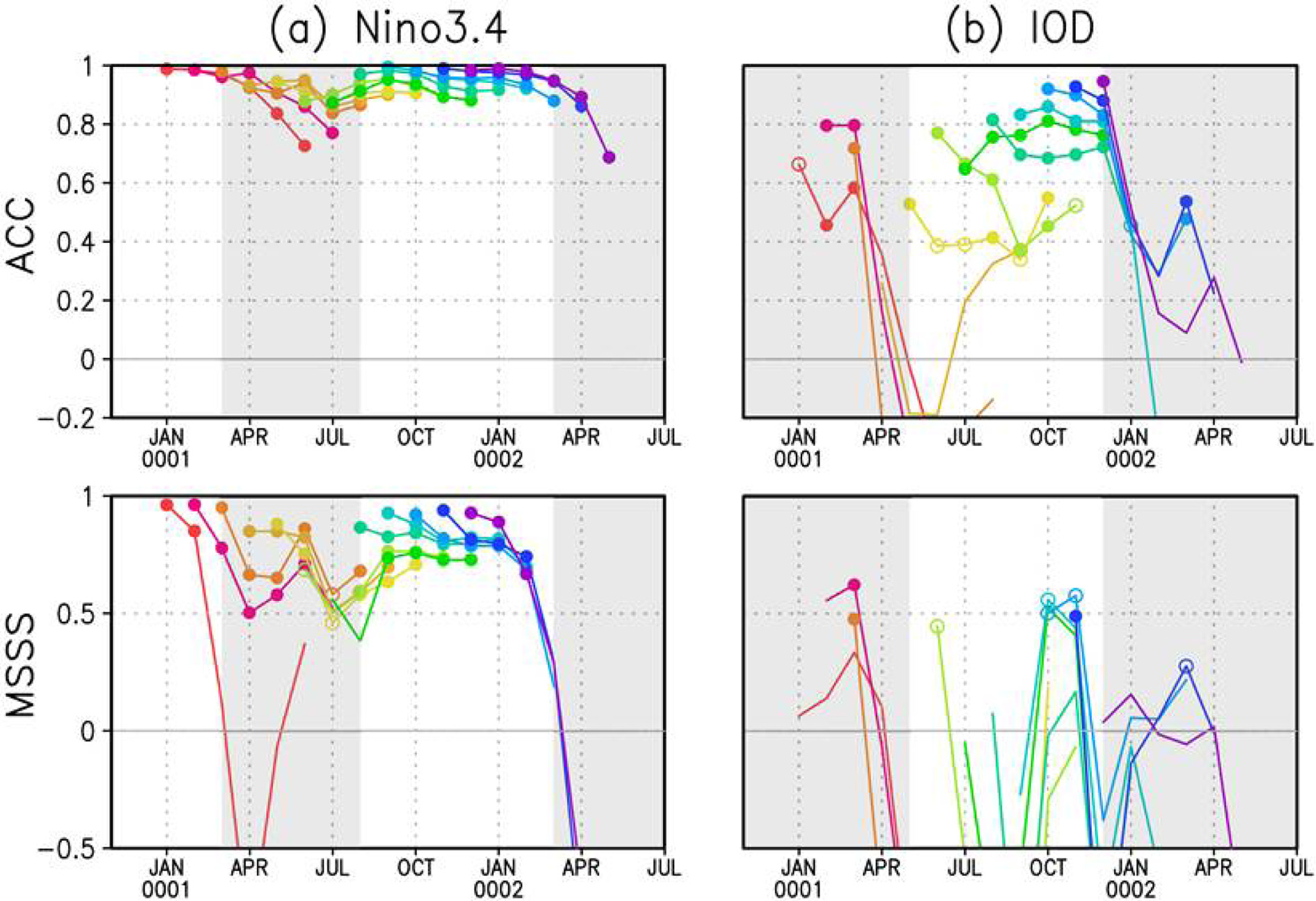
Same as Fig. 2 but for (a) Nino3.4 and (b) IOD indices. Months show the given index is not much physically meaningful are shaded in gray.

ENSO가 광범위한 열대태평양의 해양-대기 결합시스템으로 설명할 수 있다면 IOD는 주로 인도양 지역을 중점으로 한 지역적 해양-대기 결합시스템으로 설명된다(Behera et al., 1999; Iizuka et al., 2000). 이 현상은 SST가 인도양의 동부에서 낮아지고 서부에서 높아지는 현상으로 열대 서인도양과 남인도양의 SST 차이로 정의된다. IOD는 ENSO와 비슷하게 전 지구 기후시스템에 영향을 주는 것으로 알려져 있다. 양의 IOD가 발생하면 인도양에 인접한 동아프리카 지역의 집중호우와 인도네시아 지역의 가뭄 등에 직접적인 영향을 준다(Saji et al., 1999). 또한 원격상관을 통해 지리적으로 떨어진 유럽과 북미-남미 및 북동아시아의 기온과 강우에도 영향을 준다. 동아시아의 몬순 변동성에도 영향을 줄 수 있음을 선행연구에서 확인할 수 있다(Guan and Yamagata, 2003; Kripalani et al., 2005). 주로 여름철에 발생하여 10월에 가장 성장하고 그 이후에 2~3개월에 걸쳐 쇠퇴하는 짧은 수명을 가지고 있다. 따라서 월별 표준편차가 가장 큰 6월에서 11월까지의 6개월을 중점으로 분석하였다.

IOD가 발생하기 시작하는 5~6월의 경우 편차가 크기 때문에 통계적으로 유의한 수준의 예측성이 없거나 다소 떨어진다(Fig. 5b). 하지만 최대로 성장하여 그 변동성이 안정한 10월 전후의 가을철은 lead time에 상관없이 예측성이 높게 나타난다. 이러한 결과는 엘니뇨 발생 시기에 예측성이 떨어지고, 최대로 성장한 시기에 예측성이 높게 나타나는 Nino3.4의 ACC분석 결과와 비슷하다. 다만 IOD의 경우, 그 예측성이 전체적으로 Nino3.4에 비해 낮게 나타난다. MSSS는 전반적으로 그 값이 통계적으로 유의하지 않다.

6. 북극진동 및 몬순 지수의 예측성

북극진동(Arctic Oscillation, AO)은 북반구 겨울철 대기대순환에서 두드러지는 변동으로 중위도 및 고위도 기후와 밀접하게 연관되어 있다(Thompson and Wallace, 2000; Wettstein and Mearns, 2002). 특히 한파, 폭설, 강풍과 같은 극한 기상인자에 영향을 주는 것으로 알려져 있다(Higgins, 2002). AO는 동아시아 겨울철 몬순에 영향을 주기도 하고(Wu and Wang, 2002) 본 연구에서 겨울몬순 지수로 사용한 시베리아 고기압과 음의 상관관계를 가진다(Gong et al., 2001). 또한 겨울철뿐만 아니라 여름철 동아시아 몬순관련 순환과 강수에도 영향을 미치는 것으로 알려져 있다(Gong and Ho, 2003; Gong et al., 2011). 따라서 AO의 예측성 향상은 동아시아 겨울 및 여름 몬순 지수의 예측성에 일부 영향을 줄 것으로 추측된다.

본 연구에서는 Empirical Orthogonal Function (EOF)을 이용한 통계적 방법으로 정의된 AO 지수(북위 20^o이상 해면기압의 leading EOF) 대신 Li and Wang (2003)이 고안한 AO 지수를 사용하였다. 이 지수는 EOF를 이용한 지수와 마찬가지로 북반구 중위도 순환장의 변동성을 잘 나타낸다. 또한 간단한 정의로 인해 다른 자료와의 비교가 쉬워 AO 관련 선행연구에서 사용되었다(e.g., Wu et al., 2009; Jiang and Li, 2011). Figure 6a를 보면 AO는 다른 계절에 비해 11월과 12월에 초기화된 자료에서 다소 예측성이 존재하는 것으로 보인다. 그러나 다른 계절에서는 lead time 0을 제외하면 통계적으로 유의한 예측성은 없는 것으로 진단되었다.

동아시아 몬순의 변동은 아시아와 태평양 주변 지역에 사회-경제학적으로 큰 영향을 미치기 때문에 그 예측성의 향상이 중요하다(Gadgil et al., 2005; Shukla, 2007; Wang et al., 2014). 그러나 중위도 지역뿐만이 아니라 적도, 아열대 지역과 강한 상호작용을 하고 있으며 계절 내 규모에서 시간적, 공간적 변동성이 매우 큰 복잡한 시스템이기 때문에 동아시아 몬순의 계절 예측성은 몇 개월 정도로 매우 짧다. 해양-대기 결합모델의 계절예측 시스템에서도 여름몬순 순환의 예측은 최대 5개월로 알려져 있으며(Lee et al., 2011; Li et al., 2012) 이는 ENSO와 같은 기후변동에 비해 예측 가능한 lead time이 매우 짧음을 뜻한다.

계절예측시스템에서 몬순 강수량의 예측성이 좋지 않은 것은 선행연구에서 찾아볼 수 있다. 그러나 보다 큰 규모를 가지는 동아시아 여름 몬순의 순환장은 다소 예측이 가능한 것으로 알려져 있다(Lee et al., 2011; Li et al., 2012). 동아시아 지역은 북서태평양 고기압의 발달, 하층 수증기의 수송, 상층 제트기류의 영향 등 다양한 기후인자에 영향을 받고 있다. 따라서 하나의 지수만으로는 동아시아 몬순의 복잡한 시스템을 이해하기 힘들기 때문에 동아시아 몬순의 강도를 정량화하기 위해 많은 연구가 선행되었다. 동아시아 몬순 지수는 몬순의 전체적인 순환장에서 어느 지역의 어떤 특성에 주목했느냐에 따라 굉장히 다양하게 정의된다(e.g., Lau et al., 2000; Li and Zeng, 2002; Ha et al., 2005). 간단히 몇 개의 여름 몬순지수를 예로 들면 Western North Pacific Monsoon (WNPM; Wang et al., 2001)은 북서태평양 아열대 고기압과 관련한 하층의 순환을 정량화하였고, Webster-Yang (WY; Webster and Yang, 1992)은 인도 몬순의 영향을 받은 연직순환에 초점을 맞추었다.

Fig. 6.

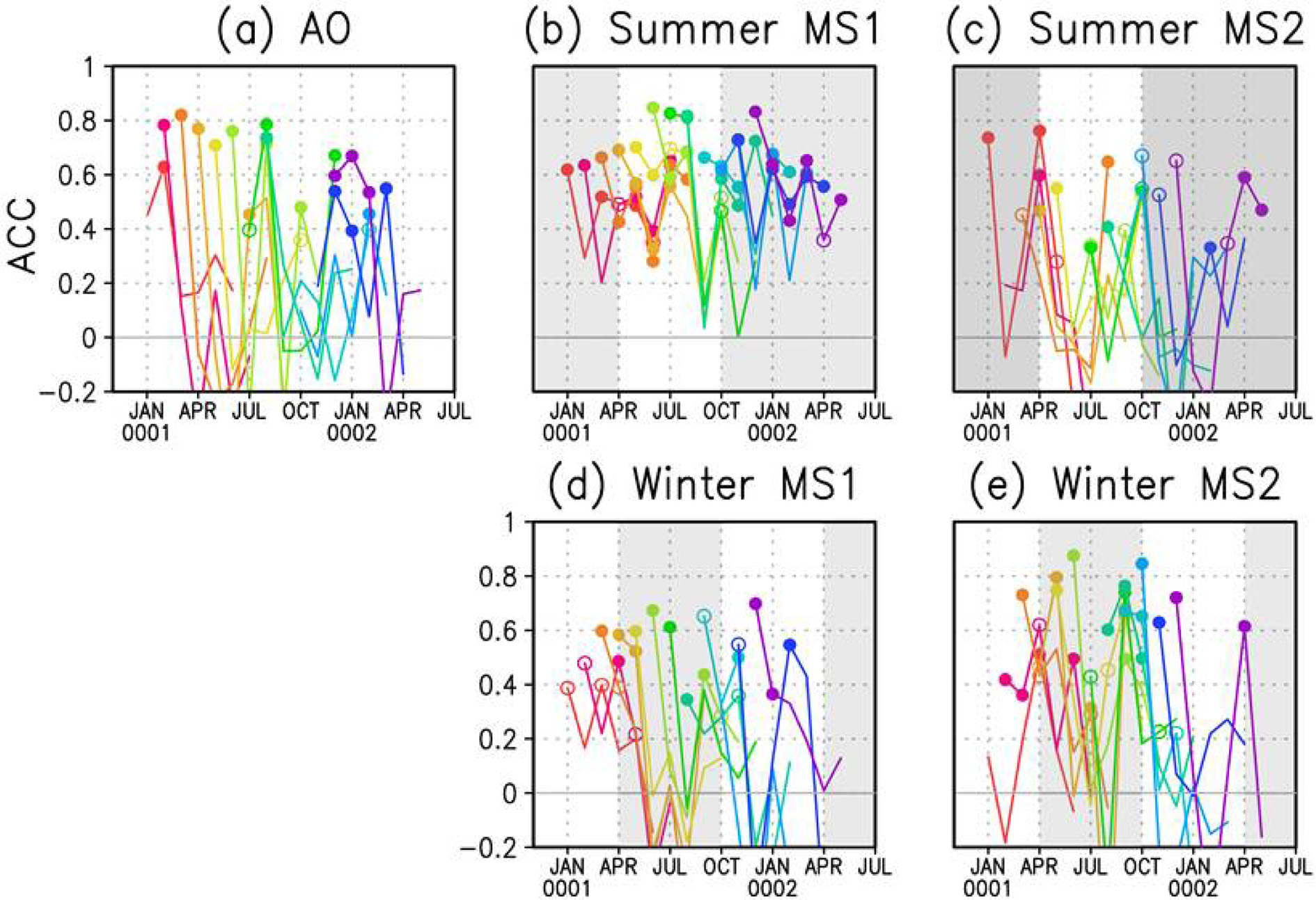
Same as Fig. 2 but only for the ACC of (a) AO, (b,c) summer monsoon and (d,e) winter monsoon indices. Months show the given index is not much physically meaningful are shaded in gray.

본 연구에서는 선행연구를 참고하여 큰 규모의 순환장을 지수화한 두 개의 여름 몬순 지수를 살펴보았다. 동아시아 여름 몬순의 예측성을 평가하기 위해 여름몬순1 지수(Wang et al., 2001)와 여름몬순2 지수(Ha et al., 2005)를 사용하였다. 이 두 지수는 동아시아 몬순 순환을 나타내는 지표로서 Table 2에 나타낸 것처럼 지역 평균된 하층 바람장을 이용하여 정의한다.

Figure 6b에서 여름몬순1은 몬순 최대기인 여름철에 높은 ACC를 가지며 10월에 급격하게 감소한다. 여름몬순 2는 lead time 0을 제외하고 예측성이 없는 것으로 보인다. 여름몬순1이 여름몬순2보다 높은 이유는 지수에서 나타나는 계절변동성이 작기 때문으로 추측된다. 선행연구에 따르면 UK Met Office (UKMO)와 Meteo-France (MF), the European Centre for Medium-Range Weather Forecasts (ECMWF) 및 the Leibniz Institute of Marine Sciences at Kiel University (IFM-GEOMAR) 등 다양한 프로젝트에서 사용하는 해양-대기 결합 모델에서 여름몬순1의 강한 경년 변동성은 5개월 정도 예측이 가능한 것으로 알려져 있다(Lee et al., 2011; Li et al., 2012). GloSea5의 이른 여름에 시작된 예측에서는 최소한 약 5개월의 예측성을 갖는 것을 확인할 수 있었다.

여름철 동아시아 몬순과 관련된 순환장들은 전년도 겨울철 ENSO의 영향을 많이 받는 것으로 알려져 있다(Wang et al., 2009). 그러나 GloSea5는 6개월 적분값이 최대 lead time이기 때문에 자료의 한계로 동아시아 몬순과 ENSO의 지연상관관계를 확인할 수 없었다. 이처럼 몇 개월의 기간을 두고 발생하는 원격 상관관계의 예측성을 파악하기 위해서는 1년 이상의 적분 자료가 추가되어야 할 것이다.

동아시아 겨울몬순은 시베리아 고기압 및 알루샨 저기압과 관계가 있으며 이들의 강화는 동아시아 지역에서 발생하는 한파 등 악기상 현상과 관련이 있다(Jhun and Lee, 2004). 또한 동아시아 겨울 몬순은 지리적으로 거리가 있는 북서태평양과 동태평양에 영향을 준다. 동아시아 겨울몬순 순환의 변동성을 예측하기 위해 수많은 선행연구들이 있다(Chang et al., 1979; Chang and Lau, 1982; Zhang et al., 1997). 여름몬순과 마찬가지로 겨울몬순 또한 몬순 순환장의 어떤 특성에 초점을 맞췄느냐에 따라 다양하게 정의되고 있다.

동아시아 겨울 몬순의 예측성을 평가하기 위해 겨울몬순1 지수(Panagiotopoulos et al., 2005)와 겨울몬순2 지수(Jhun et al., 2004)를 사용하였다. 겨울몬순2 지수를 구할 때, Jhun and Lee (2004)에서는 300 hPa의 U-wind 값을 제안하였지만 본 연구에서는 자료의 한계로 200 hPa의 U-wind를 사용하였다. Figures 6d와 6e의 결과를 살펴보면 겨울몬순1에서 lead time 0은 일부 통계적으로 유의한 예측성을 가지나 lead time이 증가할수록 거의 예측성이 없는 것으로 판단된다. 겨울몬순2도 비슷한 결과를 나타낸다. 따라서 동아시아 겨울몬순에 대한 계절 예측성은 lead time 0의 일부분을 제외하고 없다고 본다.

Fig. 7.

Same as Fig. 3 but for precipitation.

7. 결론 및 토의

본 연구에서 살펴본 GMSAT는 대체적으로 높은 ACC를 가지며 가을철에 높고 겨울에 다소 낮게 모의되는 경향이 있다. ACC가 높은 이유는 1) 전지구 평균이기 때문에 GMSAT 자체의 변동성이 작아 보다 예측하기 쉽고 2) 지역평균시 위도별 반영비율을 고려하면 적도 해양 지역의 높은 예측성이 크게 반영되었기 때문이다. 해양 중 특히 동태평양의 예측성이 높은데 이는 열대지역의 계절 변동을 나타내는 Nino3.4로도 확인할 수 있다. ENSO는 지리적으로 가까운 인근지역뿐 아니라 원격 상관을 통해 중위도지역의 기후 · 기상 인자에도 영향을 준다. 따라서 Nino3.4의 예측성을 증가시키면 EASAT와 동아시아 몬순의 예측성도 향상될 것으로 기대된다.

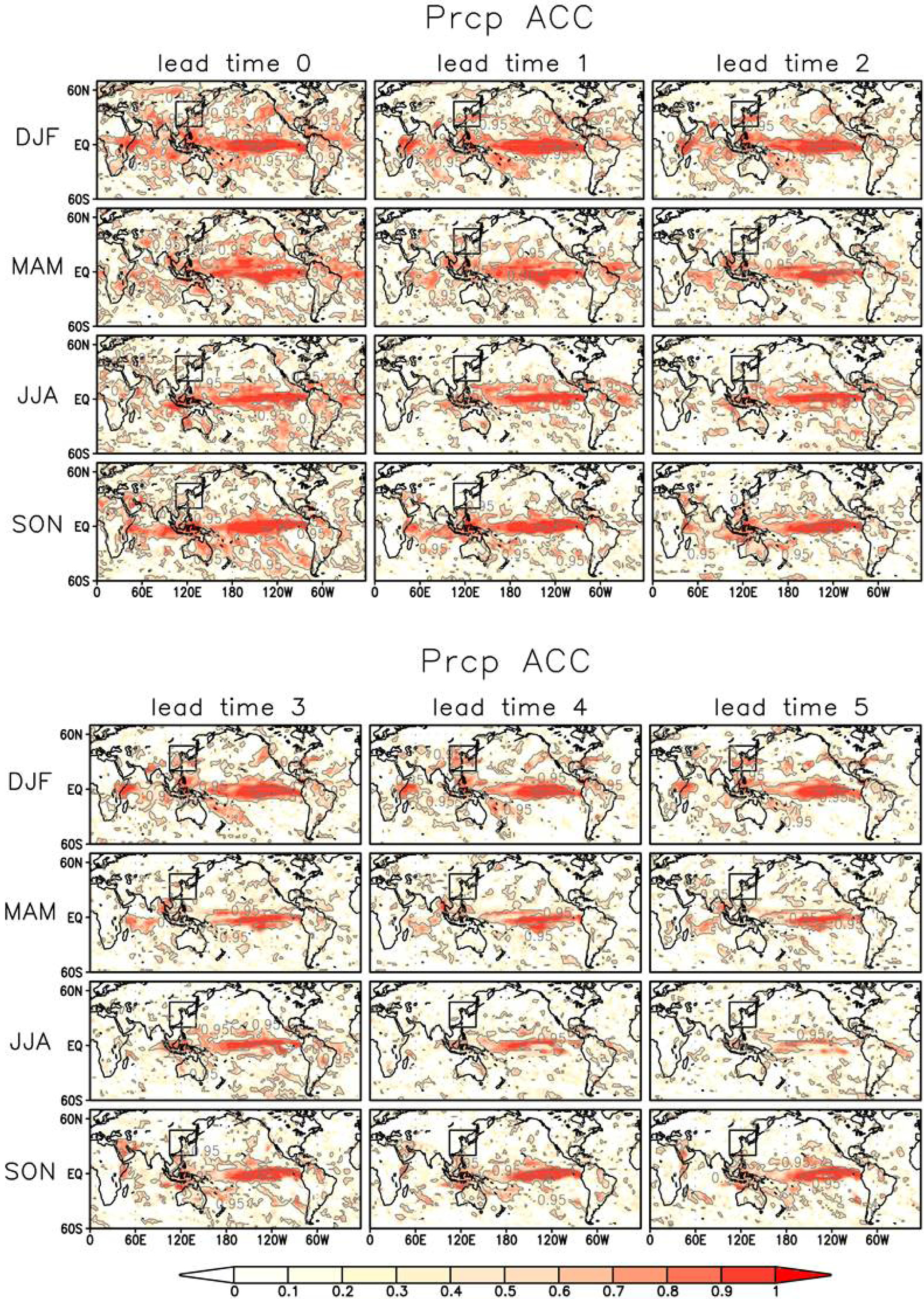
본 연구는 SAT와 동아시아 기후 변동성에 영향을 끼치는 주요 기후 인자를 중심으로 예측성을 평가하였다. SAT 및 순환장만큼 중요한 변수인 강수량에 대한 분석은 자세하게 이루어지지 않았다. 이는 강수량이 중위도에서 큰 예측성을 보이지 않았기 때문이다. Figure 7은 계절별 강수량의 ACC를 보여준다. 강수는 겨울철 lead time 0일 때, 열대 서태평양보다 열대 동태평양 지역에서 다소 우수한 예측성을 보이며, 이는 Fig. 3의 SST 예측성 결과와 일치한다. 그러나 인도양 지역의 강수 예측성은 거의 없는 것으로 판단된다. 다른 계절 또한 겨울철에 비해 비교적 낮은 예측성을 가지지만 비슷한 공간 분포를 보인다. 전반적으로 강수량의 예측은 매우 짧은 lead time에도 ACC가 낮다. 따라서 강수의 계절 예측에 있어서 많은 한계가 있는 것으로 판단된다. 무엇보다 강수는 SAT와 마찬가지로 대륙 지역의 변동성은 거의 모의하지 못한다.

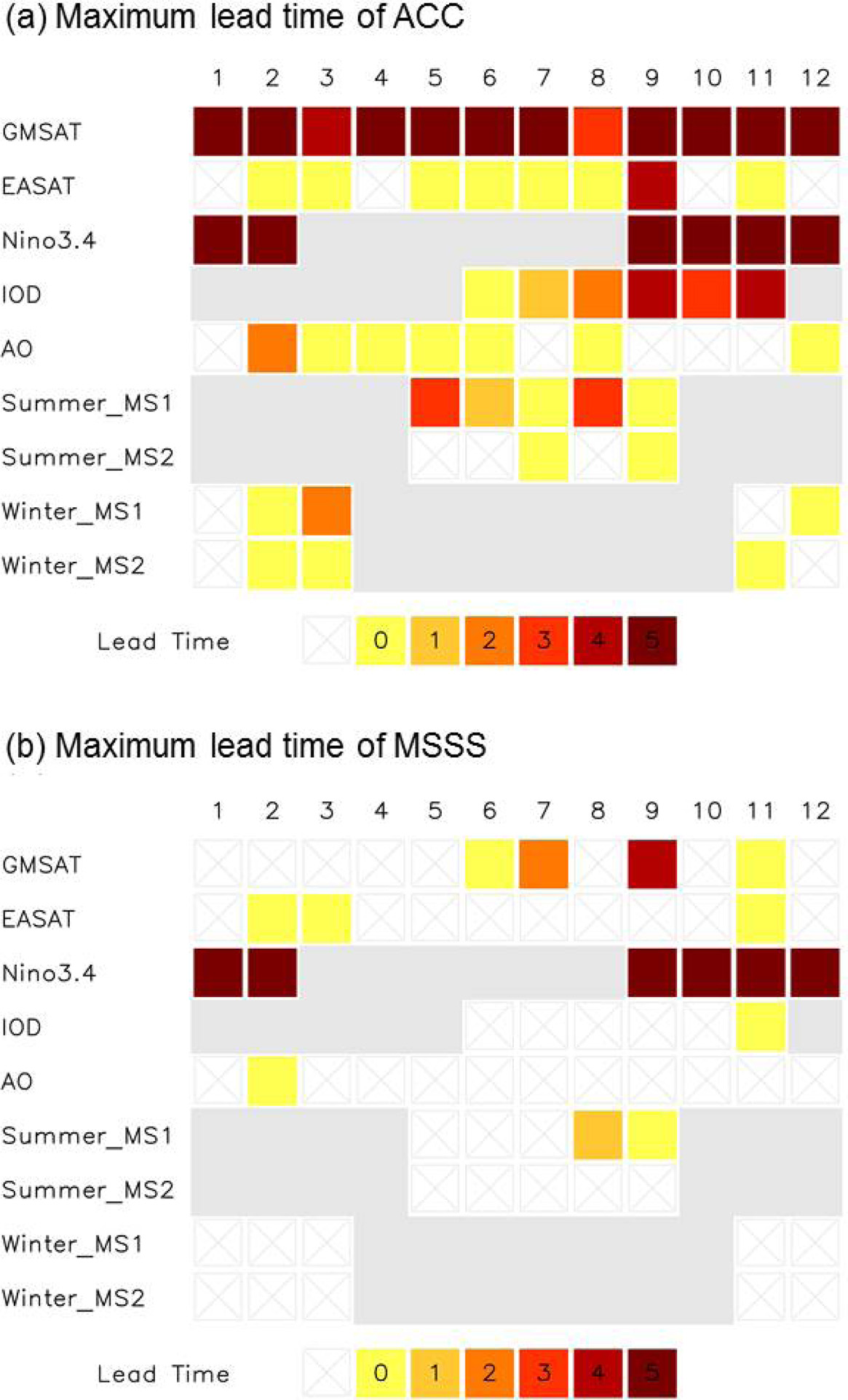
Figure 8a는 각 지수의 계절 예측이 몇 개월 전부터 가능한지를 종합적으로 보여준다. 일반적으로 예측성 평가시 ACC를 이용한다는 점을 이용해 예측성을 ACC가 통계적으로 유의한 lead time으로 정의하였다. 특히 해당월에 ACC가 통계적으로 유의하지 않더라도 전후 각 한 달 동안 ACC가 통계적으로 유의한 값을 가지면 예측성이 있는 것으로 간주하였다. 그 결과 GMSAT와 Nino3.4는 6개월 전부터 예측이 가능하고 IOD는 늦여름, 가을철의 예측이 5~6개월 전부터 가능한 것으로 나타났다. AO의 경우 겨울철과 봄철에서만 통계적으로 유의한 예측성이 보였다. 여름철 동아시아 몬순 지수 중 여름몬순1 지수는 4~6개월 전부터 예측이 가능하나 다른 몬순 지수는 예측성이 없는 것으로 판단된다.

동일한 분석을 MSSS에 대해서도 진행하였다(Fig. 8b). MSSS는 ACC와 조건부 오차를 동시에 고려한 진단 지수로 기존에 ACC가 관측과 모형 간의 분산차이를 고려하지 못하는 단점을 보완한다. Nino3.4의 경우 ACC가 높았고 지수 자체가 가지는 계절변동이 적어 MSSS도 높게 평가되지만, 다른 기후 지수들의 경우 MSSS를 이용할 때 기후 지수 예측성이 매우 떨어지는 것을 볼 수 있다. 이는 모형에서 예측된 기후지수의 선형추세 및 분산이 관측에서 나타나는 것과 상당 부분 다르다는 것을 의미한다. 이를 종합적으로 판단하면 GloSea5의 경우 GMSAT와 Nino3.4처럼 계절변동이 적은 지수는 6개월 전부터 예측이 가능한 것으로 보인다. 하지만 비교적 계절변동이 심하고 메모리가 짧은 나머지 지수들의 예측성은 낮게 나타난다.

Fig. 8.

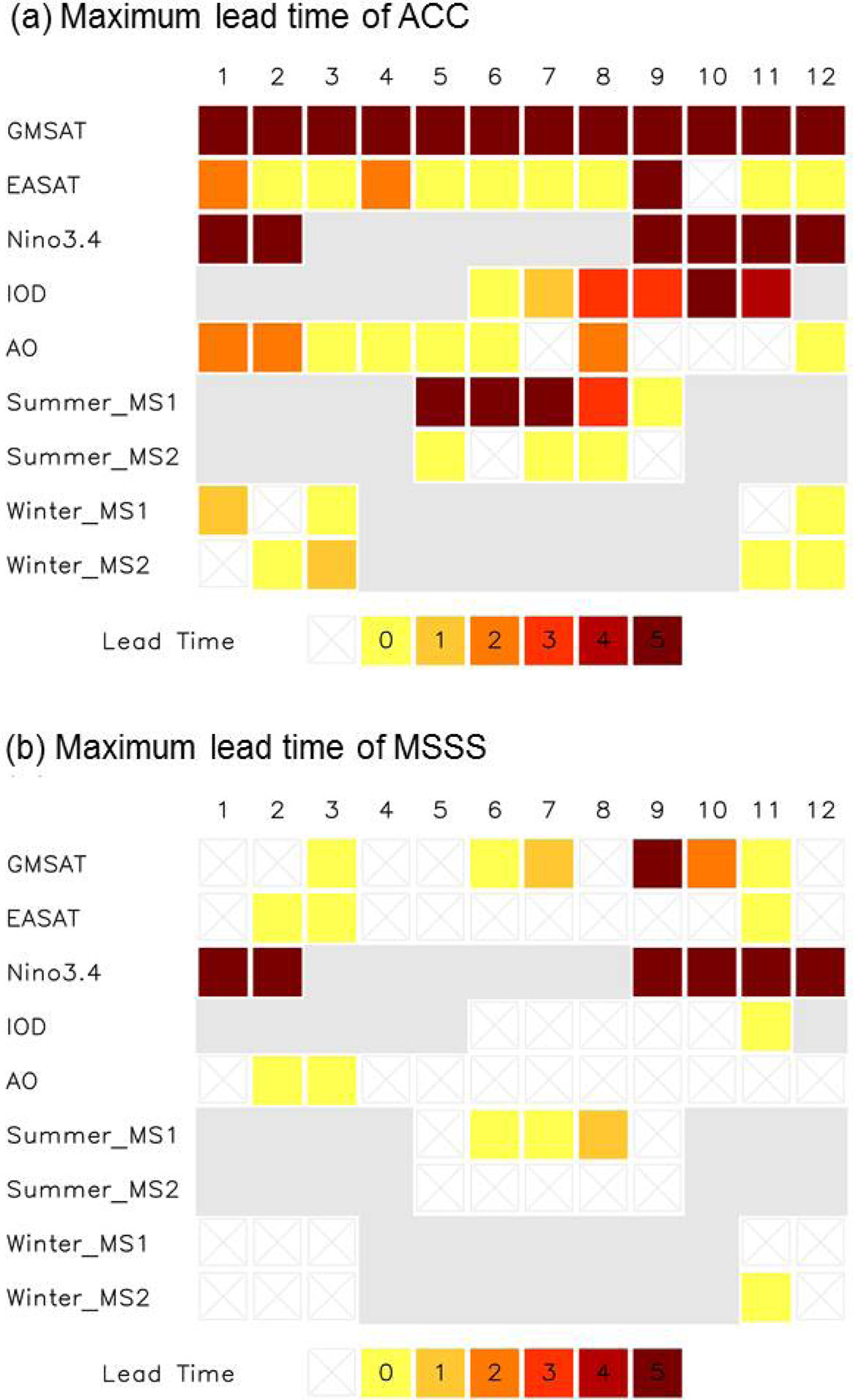
Maximum lead time of (a) ACC and (b) MSSS for each index. Months when the given index is not much physically meaningful are shaded in gray.

GloSea5는 매월 총 4일의 초기장이 존재하는데, 본 연구에서는 자료의 한계로 인해 각 초기장마다 1~3개의 앙상블을 평균한 후 분석하였다. 월평균 자료를 얻기 위해 25, 1, 9일 초기장에서 적분된 값을 평균하였고, 이에 따라 월평균 자료는 총 3~9개의 앙상블의 평균으로 계산될 수 있다. 초기장에 따라 앙상블 개수가 다르기 때문에 이로 인해 모델의 예측성을 과소평가할 가능성이 존재한다. 따라서 예측성이 앙상블 개수에 민감한가를 살펴보기 위해 추가적으로 앙상블 멤버수에 대한 민감도 분석을 수행하였다. 3~9개의 앙상블 평균으로 이루어진 자료 분석과 비교하기 위해서 각 일별 초기장에서 1개의 앙상블을 임의로 채택하여 총 3개의 앙상블로 이루어진 월평균 자료를 구하였다. 그 결과는 Fig. 9에서 볼 수 있다.

Figures 9와 8을 비교해 보면 앙상블 개수가 줄어들 경우 여름몬순 1에서 비교적 큰 차이를 보였다. 하지만 다른 지수에서는 큰 변화를 보이지 않았으며 오히려 예측 가능한 시점이 늘어난 지수(겨울몬순1)도 있었다. 이를 통해 GloSea5의 예측성은 9개 이하의 앙상블 멤버에서는 그 수에 아주 민감하지 않음을 확인할 수 있다. 즉 예측성이 좋지 못한 지수들의 경우에 9개의 앙상블 멤버를 모두 갖춘 후 예측성을 평가하더라도 현재 결과와 큰 차이를 보이지 않을 것으로 판단된다. 그러나 이는 현재 앙상블 멤버의 생산 방법(Lagged Average Forecast)에 따른 문제일 수 있기 때문에 향후 다양한 앙상블 멤버 생산 방법을 이용한 예측성 평가 연구가 요구된다. 따라서 GloSea5의 예측성을 향상시키기 위해서는 앙상블 멤버 수를 조금 늘리기보다는 앙상블 멤버 생산 방법의 개선 또는 해상도를 높이거나 물리과정을 수정하는 등의 모형 개선에 더 주목해야 할 것으로 판단된다. 또한 예측성이 높은 기후 지수의 원격 상관 또는 여러 기후 지수의 다중 상관 관계를 이용한 예측성 향상에 대한 추가 연구도 요구된다.

Fig. 9.

Same as Fig. 8 but for the results using only three ensemble members.

Acknowledgments

본 연구는 국립기상연구소 주요사업 “한영 공동기후예측시스템 진단체계 구축(II) (NIMR-2012-B-2)” 및 2013년도 정부(교육부)의 재원으로 한국연구재단(No.2013R1A1A1006530)의 지원을 받아 수행되었습니다.

REFERENCES

• Alberto, A., and Coauthors , (2011), The GloSea4 ensemble prediction system for seasonal forecasting, Mon. Wea. Rev., 139, p1891-1910. [https://doi.org/10.1175/2010MWR3615.1]
• Adler, R. F., and Coauthors , (2003), The version-2 Global Precipitation Climatology Project (GPCP) monthly precipitation analysis (1979-present), J. Hydrometeor., 4, p1147-1167. [https://doi.org/10.1175/1525-7541(2003)004<1147:TVGPCP>2.0.CO;2]
• Behera, S. K., R. Krishnan, and T. Yamagata, (1999), Unusual ocean-atmosphere conditions in the tropical Indian Ocean during 1994, Geophys. Res. Lett., 26, p3001-3004. [https://doi.org/10.1029/1999GL010434]
• Cha, E.-J., J.-G. Jhun, and H.-S. Chung, (1999), A study of characteristics of climate in South Korea for El Niño/ La Niña Years, Asia-Pac. J. Atmos. Soc., 35, p98-117.
• Chang, C.-P., and K.-M. Lau, (1982), Short-term planetaryscale interaction over the tropics and the midlatitudes during northern winter. Part I: Contrast between active and inactive periods, Mon. Wea. Rev., 110, p933-946. [https://doi.org/10.1175/1520-0493(1982)110<0933:STPSIO>2.0.CO;2]
• Chang, C.-P., J. Erickson, and K.-M. Lau, (1979), Northeasterly cold surges and near-equatorial disturbances over the winter-MONEX area during 1974. Part I: Synoptic aspects, Mon. Wea. Rev., 107, p812-829. [https://doi.org/10.1175/1520-0493(1979)107<0812:ncsane>2.0.co;2]
• Choi, J., S.-W. Son, Y.-G. Ham, J.-Y. Lee, and H.-M. Kim, (2015), Seasonal to interannual prediction skills of near-surface air temperature in the CMIP5 decadal hindcast experiments, in revision.
• Gadgil, S., M. Rajeevan, and R. Nanjundiah, (2005), Monsoon prediction-Why yet another failure?, Curr. Sci., 88, p1389-1400.
• Goddard, L., and Coauthors , (2013), A verification framework for interannual-to-decadal predictions experiments, Clim. Dynam., 40, p245-272. [https://doi.org/10.1007/s00382-012-1481-2]
• Gong, D.-Y., and C.-H. Ho, (2003), Arctic Oscillation signals in the East Asian summer monsoon, Geophy. Res. Lett., 108, p4066. [https://doi.org/10.1029/2002JD002193]
• Gong, D.-Y., S. W. Wang, and J. H. Shu, (2001), East Asian winter monsoon and Arctic Oscillation, Geophys. Res. Lett., 28, p2073-2076. [https://doi.org/10.1029/2000GL012311]
• Gong, D.-Y., and Coauthors , (2011), Spring Arctic Oscillation- East Asian summer monsoon connection through circulation changes over the western North Pacific, Clim. Dynam., 37, p2199-2216. [https://doi.org/10.1007/s00382-011-1041-1]
• Guan, z., and T. Tamagata, (2003), The unusual summer of 1994 in East Asia: IOD teleconnections, Geophys. Res. Lett., 30, p1544-1547. [https://doi.org/10.1029/2002GL016831]
• Guilyardi, E., A. Wittenberg, A. Fedorov, M. Collins, C. Wang, A. Capotondi, G. J. Van Oldenborgh, and T. Stockdale, (2009), Understanding El Nino in oceanatmosphere general circulation models: Progress and challenges, Bull. Amer. Meteor. Soc., 90, p325-340. [https://doi.org/10.1175/2008BAMS2387.1]
• Gupta, A. S., L. C. Muir, J. N. Brown, S. J. Phipps, P. J. Durack, D. Monselesan, and S. E. Wijffels, (2012), Climate Drift in the CMIP3 Models, J. Climate, 25, p4621-4640. [https://doi.org/10.1175/JCLI-D-11-00312.1]
• Ha, K.-J., S.-K. Park, and K.-Y. Kim, (2005), On interannual characteristics of climate prediction center Merged analysis precipitation over the Korean Peninsula during the summer monsoon season, Int. J. Climatol., 25, p99-116. [https://doi.org/10.1002/joc.1116]
• Horel, J. D., and J. M. Wallace, (1981), Planetary scale atmospheric phenomena associated with the Southern Oscillation, Mon. Wea. Rev., 125, p773-788. [https://doi.org/10.1175/1520-0493(1981)109<0813:psapaw>2.0.co;2]
• Hurrell, J., A. M. Gerald, B. David, L. D. Thomas, K. Ben, and W. Bruce, (2009), A unified modeling approach to climate system prediction, Bull. Amer. Meteor. Soc., 90, p1819-1832. [https://doi.org/10.1175/2009BAMS2752.1]
• Jiang, X., and Y. Li, (2011), Spatio-temporal variability of winter temperature and precipitation in southwestern China and possible causes, J. Geogr. Sci., 21, p250-262. [https://doi.org/10.1007/s11442-011-0842-9]
• Jin, E. K., and Coauthors , (2008), Current status of ENSO prediction skill in coupled ocean-atmosphere models, Clim. Dynam., 31, p647-664. [https://doi.org/10.1007/s00382-008-0397-3]
• Kang, H. S., K. O. Boo, and C. H. Cho, (2011), Introduction to KMA-Met office joint seasonal forecasting system and evaluation of its hindcast ensemble simulations, NOAA/NWS Science and Technology Infusion Climate Bulletin, Oct, 2011.
• Kang, I.-S., (1998), Relationship between El-Nino and Korean climate variability, J. Korean Meteor. Soc., 34, p390-395.
• Kim, H.-M., P. J. Webster, and J. A. Curry, (2012), Evaluation of short-term climate change prediction in multimodel CMIP5 decadal hindcasts, Geophys. Res. Lett., 39, pL10701. [https://doi.org/10.1029/2012GL051644]
• Kripalani, R. H., J. H. Oh, J. H. Kang, S. S. Sabade, and A. Kulkarni, (2005), Extreme monsoons over East Asia: Possible role of Indian Ocean Zonal Mode, Theor. Appl. Climatol., 82, p81-94. [https://doi.org/10.1007/s00704-004-0114-z]
• Lee, S. S., and Coauthors , (2011), Deficiencies and possibilities for long-lead coupled climate prediction of the Western North Pacific-East Asian summer monsoon, Clim. Dynam., 36, p1173-1188. [https://doi.org/10.1007/s00382-010-0832-0]
• Li, C., R. Lu, and B. Dong, (2012), Predictability of the western North Pacific summer climate demonstrated by the coupled models of ENSEMBLES, Clim. Dynam., 39, p329-346. [https://doi.org/10.1007/s00382-011-1274-z]
• Luo, J. J., S. Masson, S. K. Behera, and T. Yamagata, (2008), Extended ENSO predictions using a fully coupled ocean-atmosphere model, J. Climate, 21, p84-93. [https://doi.org/10.1175/2007JCLI1412.1]
• Luo, J. J., S. Masson, E. Roeckner, G. Madec, and T. Yamagata, (2005), Reducing climatology bias in an ocean-atmosphere CGCM with improved coupling physics, J. Climate, 18, p2344-2360. [https://doi.org/10.1175/JCLI3404.1]
• Luo, J. J., and Coauthors , (2014), Decadal climate prediction: An update from the trenches, Bull. Amer. Meteor. Soc., 95, p243-267. [https://doi.org/10.1175/BAMS-D-12-00241.1]
• MacLachlan, C., and Coauthors , (2014), Global Seasonal forecast system version 5 (GloSea5): A high-resolution seasonal forecast system, Quart. J. Roy. Meteor. Soc. [https://doi.org/10.1002/qj.2396]
• Moore, A. M., and R. Kleeman, (1996), The dynamics of error growth and predictability in a coupled model of ENSO, Quart. J. Roy. Meteor. Soc., 122, p1405-1446. [https://doi.org/10.1002/qj.49712253409]
• Outten, S. D., R. Davy, and I. Esau, (2013), Eurasian winter cooling: Intercomparison of reanalyses and CMIP5 data sets, Atmos. Oceanic Sci. Lett., 6, p324-331. [https://doi.org/10.3878/j.issn.1674-2834.12.0112]
• Panagiotopoulos, F., M. Shahgedanova, A. Hannachi, and D. B. Stephenson, (2005), Observed trends and teleconnections of the Siberian high: A recently declining center of action, J. Climate, 18, p1411-1422. [https://doi.org/10.1175/JCLI3352.1]
• Saji, N. H., B. N. Goswami, P. N. Vinayachandran, and T. Yamagata, (1999), A dipole mode in the tropical Indian Ocean, Nature, 401, p360-363. [https://doi.org/10.1038/43854]
• Sarachik, E. S., and M. A. Cane, (2010), The El Nino-Southern Oscillation Phenomenon, Cambridge 461 Univ. Press, New York, p369. [https://doi.org/10.1017/CBO9780511817496]
• Shukla, J., (2007), Monsoon Mysteries, Science, 318, p204-205. [https://doi.org/10.1126/science.1150045]
• Thompson, D. W. J., and J. M. Wallace, (2000), Annular modes in the extratropical circulation. Part I: Monthto- month variability, J. Climate, 13, p1000-1016. [https://doi.org/10.1175/1520-0442(2000)013<1000:AMITEC>2.0.CO;2]
• Van Oldenborgh, G. J., F. J. Doblas-Reyes, B. Wouters, and W. Hazeleger, (2012), Skill in the trend and internal variability in a multi-model decadal prediction ensemble, Clim. Dynam., in press.
• Wang, B., B. Xiang, and J.-Y. Lee, (2012), Subtropical high predictability establishes a promising way for monsoon and tropical storm predictions, Proc. Natl. Acad. Sci. U. S. A., 110, p2718-2722. [https://doi.org/10.1073/pnas.1214626110]
• Wang, B., B. Xiang, and J.-Y. Lee, (2014), Asian summer monsoon rainfall predictability: A predictable mode analysis, Clim. Dynam., 44, p61-74. [https://doi.org/10.1007/s00382-014-2218-1]
• Wang, B., and Coauthors , (2009), Advanced and prospectus of seasonal prediction: assessment of APCC/CliPAS 14- model ensemble retrospective seasonal prediction (1980~2004), Clim. Dynam., 33, p93-117. [https://doi.org/10.1007/s00382-008-0460-0]
• Webster, P. J., and S. Yang, (1992), Monsoon and ENSO: Selectively interactive systems, Quart. J. Roy. Meteor. Soc., 118, p877-926. [https://doi.org/10.1002/qj.49711850705]
• Wettstein, J. J., and L. O. Mearns, (2002), The influence of the North Atlantic-Arctic Oscillation on mean, variance and extremes of temperature in the northeastern United States and Canada, J. Climate, 15, p3586-3600. [https://doi.org/10.1175/1520-0442(2002)015<3586:TIOTNA>2.0.CO;2]
• Wu, B., and J. Wang, (2002), Winter Arctic Oscillation, Siberian High and east Asian winter monsoon, Geophys. Res. Lett., 29, 3-1-3-4. [https://doi.org/10.1029/2002GL015373]
• Wu, Z., J. Li, B. Wang, and X. Liu, (2009), Can the Southern Hemisphere annular mode affect China winter monsoon?, J. Geophys. Res., 114, pD11107. [https://doi.org/10.1029/2008jd011501]
• Zhang, Y., K. R. Sperber, and J. S. Boyle, (1997), Climatology and interannual variation of the East Asia winter monsoon: Results from the 1979-95 NCEP-NCAR reanalysis, Mon. Wea. Rev., 125, p2605-2619. [https://doi.org/10.1175/1520-0493(1997)125<2605:CAIVOT>2.0.CO;2]