CICE5 해빙 시공간 분포 모의 평가 및 파라미터 민감도 테스트

1. 서 론

전지구적인 온난화에 따라서 기후변화에 의해 북극 해빙의 감소가 가속화 되고 있다(Ricker et al., 2017; Stroeve et al., 2018; Yadav et al., 2020). 특히, 북극은 전지구 평균온도에 비해 4배 정도 빠르게 온도가 상승하고 있으며 이로 인해 고위도 및 중위도 기후변동성에 큰 영향을 주고 있어 북극 해빙변동성에 대한 관심이 증가하고 있다(Vihma 2014; Walsh 2014; Wu et al., 2016). 북극 해빙의 감소는 대기와 해양 간의 에너지 교환에 직접적인 영향을 미치고 있으며 중위도 지역에서 계절 내 규모 기후변동성 및 극한 기후 현상의 빈도와 강도의 변동성에 영향을 주는 주요 원인으로 작용하고 있다(Francis and Vavrus, 2012; Cohen et al., 2014, 2020). 특히, 북극의 겨울철 해빙변동성은 우리나라를 포함한 동아시아 지역의 극한 한파 및 폭설과 같은 기상 현상에 영향을 준다(Kug et al., 2015; He et al., 2017; Xu et al., 2021). 예를들어, 바렌츠해의 해빙 감소는 대기중으로 열을 방출시켜서 대기순환에 변화를 일으켜 북극진동의 약화와 시베리아 고기압의 강화 등을 통해 우리나라 한파에 영향을 준다고 알려져 있다(Kim et al., 2014; Kim et al., 2022). 이처럼 해빙 변동성은 우리나라 기후 및 날씨에 큰 영향을 주는 중요 요인이며 우리나라 기후 및 기상 예측 기술의 향상에 해빙 변동성에 대한 물리적인 이해와 예측 기술의 발전이 필요하다.

해빙의 물리적 과정은 대기-해양 간의 상호작용을 통해 전 지구적인 기후 시스템에 중요한 영향을 미치며, 이러한 상호작용을 정확하게 모사하는 해빙 모형은 기후 예측의 중요한 도구로 자리 잡고 있다(Hunke et al., 2011). 해빙의 생성과 손실은 지구 에너지 균형, 대기와 해양 간의 열 및 물질 교환에 중요한 역할을 하며, 이러한 과정들이 기후 변화에 어떻게 영향을 미치는지 분석하는 데 있어 해빙 모형의 중요성이 더욱 강조되고 있다(Sun et al., 2020). 해빙 모형의 성능을 향상시키기 위해서 해빙 모형의 역학과 열역학 시뮬레이션에 사용되는 여러 요소들의 물리적인 체계개선(Bouchat et al., 2022; Boutin et al., 2023) 및 성분요소의 민감도(Lee and Ahn, 2014), 여러 관측과 재분석 자료를 이용한 자료동화와(Mu et al., 2020; Yang et al., 2020) 해빙 모형의 파라미터 개선(Bouchat et al., 2022; Zhang et al., 2022) 등 여러 노력이 진행되고 있다. 특히, 해빙 모형의 파라미터는 해빙의 성장, 녹음, 이동 및 역학적, 열역학적 과정을 모사하는 데 중요한 역할을 한다(Bailey et al., 2020; Zhang, 2021). 이들 파라미터는 모델 결과에 큰 영향을 미치며, 따라서 해빙 모형의 성능을 향상시키기 위해서는 이러한 파라미터의 민감도를 분석하고 최적화할 필요가 있다. 민감도 실험은 각 파라미터의 변화가 모델의 예측 결과에 미치는 영향을 평가하는 방법으로, 이를 통해 모델의 신뢰성을 높임으로 전지구 기후 예측 정확성을 높일 수 있다.

본 연구에서는 Los Alamos National Laboratory (LANL)에서 개발한 전지구 해빙 모형을 사용하여(Hunke et al., 2015), 해빙의 물리 파라미터의 변화가 북반구 해빙 면적 및 해빙 부피의 계절적 변동성과 경년 변동성에 미치는 민감도를 분석하고자 한다. 이를 통해 CICE5 모형의 파라미터 최적화와 이를 통한 물리과정의 개선을 도모할 수 있는 기초 정보를 축척하고자 하는 것이다. 사용한 해빙 모형과 강제력에 대한 정보와 모델 검증에 사용한 관측 및 재분석 자료, 파라미터 실험에서 쓰이는 파라미터들에 대한 정보, 민감도 실험의 방법을 2장에서 제공한다. 3장에서는 해빙 모델이 검증과 파라미터 실험 결과의 분석을 제시했다. 마지막으로 4장에서는 3장에서 분석한 연구결과 요약 및 한계를 제시한다.

2. 모델 및 실험방법

2.3 파라미터

CICE5 해빙모형에서는 복잡한 물리과정과 복잡한 상호작용, 소규모 스케일의 시뮬레이션등의 계산상의 어려움을 간소화하기 위해서 물리과정을 모수화하는 부분들이 존재한다. 예를 들어 해빙의 이동에 따른 해빙의 릿지(ridge)형성과 같은 부분을 직접 모델링하는 것은 어렵기 때문에 이와 관련된 과정을 파라미터화하여 계산한다. 이 연구에서 민감도 실험에 사용된 파라미터(Table 1)는 복사 과정을 담당하는 눈과 얼음의 방출율(emissivity of snow and ice, ε), 눈과 얼음의 알베도 계산에 필요한 알베도 튜닝 파라미터인 R_ice R_snow, 열역학적 과정을 담당하는 얼음과 눈 밀도(ρ_i and ρ_s), 눈과 얼음의 열전도도(k₀ and k_s) 및 역학 과정을 담당하는 파라미터들(C_f, C_s, F_srdg, and E₀)을 사용했다. 각 파라미터의 간단한 설명과 규준 실험에서 사용한 기본값(default value)을 Table 1에 제시했다.

Table 1.

Description of parameters used in sensitivity experiments.

3. 결과 및 분석

3.1 CICE5의 해빙 농도와 해빙 두께 모의 평가

해빙 모형에 1979년부터 2018년기간인 40년 동안 ERA5 대기 강제력을 처방한 규준 실험을 관측과 비교해 CICE5의 기후학적 시공간 분포 모의 진단을 했다. 해빙 면적의 경우 CICE5는 북반구 봄철에 최대값을 가지고 여름철에 최소값을 가지고 있으며 관측과 비교해 계절 주기를 준수하게 모의하는 것으로 나타난다(Fig. 1a). 하지만, 모델과 관측 모두 해빙 면적이 9월에 최소값을 가지지만 최대값을 가지는 시기는 모델과 관측에서 다르게 나타난다. 관측에서는 3월에 해빙 면적이 가장 큰 것으로 나타나지만 모델에서는 5월에 해빙 면적이 가장 큰 것으로 나타난다. 5~9월까지 모델은 관측에 비해서 해빙 면적을 과대모의하는 것으로 나타난다. 상관관계는 0.93이며 평균 제곱근 오차(root mean square error; RMSE)는 1.3으로 나타난다. 한편 Fig. 1a를 다시 보면 모델에서의 최대치가 지체(lag)되는 느낌을 주는데 현실에서는 최대 이후에 늦봄과 여름이 되면서 태양복사의 충분한 일사가 진행되면서 해빙이 녹게 되지만 모델에서는 이러한 과정이 다소 현실적이지 못하게 반영되어 여름철 모의가 관측에 비해 과대하게 나타나는 것으로 유추 할 수 있다.

Fig. 1.

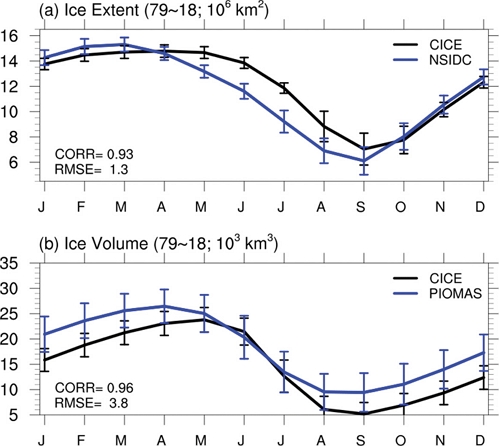
Seasonal cycle of (a) sea ice extent and (b) sea ice volume of simulated CICE5 using ERA5 atmospheric forcing (black) and observations (blue; sea ice extent from NSIDC and sea ice volume calculated using PIOMAS) from 1979 to 2018. Vertical bars represent the range of ±1.0 standard deviations over 40 years.

CICE5는 해빙 부피의 계절 주기도 어느 정도 잘 모의하는 것으로 나타난다(Fig. 1b). 해빙 면적과 마찬가지로 해빙 부피 또한 관측과 모형에서 모두 9월에 최소값을 가지지만 최대값이 나타나는 시기는 관측과 모형에서 다르게 나타난다. 모형에서는 5월에 해빙 부피의 최대값이 나타나지만 관측에서는 4월에 최대값을 가진다. 전체적으로 모형이 관측과 유사한 계절 변동성을 보여주지만 모형이 관측에 비해서 해빙 부피를 과소 모의하는 경향이 나타나며 RMSE는 8.3의 값을 가진다.

이렇게 해빙 모형에서 계절적 편차가 나타나는 이유는 해빙 모형에 처방한 해수면 온도의 편향(bias)과 관련이 있을 수 있다. ERA5 대기 강제력과 해수면 온도를 기반으로 계산된 해빙 모형의 해수면 온도를 NOAA OISST (Reynolds et al., 2007)와 비교한 결과, 계절에 따라 SST에 편향이 존재함을 확인할 수 있다(Fig. 2). 특히, 해빙 면적이 과대 모의되는 5월부터 10월 사이에는 그린란드해와 바렌츠해에서 북극해 방향으로 음의 SST 편향이 두드러졌으며 이는 모형에서 해빙이 과도하게 반응하는 현상과 관련된 것으로 보인다. 이러한 해빙 모형의 해수면 온도 편향은 ERA5 해수면 온도 자체의 문제와 함께 해수면 온도의 편향이 해빙 모형에서 해빙을 과하게 반응시킬 수 있는 것과 관련이 있다(Guemas et al., 2014; Sun and Solomon, 2024). 따라서, 해빙 모형을 단독으로 시뮬레이션할 때는 해수면 온도를 강제력으로 직접 주입하는 방법 대신 해빙 모형 내부에서 해수면 온도가 계산되도록 하고 ocean deep heat flux를 이용해 해빙의 반응을 조절하거나(Turner and Hunke, 2015; Sun and Solomon, 2024) 북극해 가장자리 부근에만 해수면 온도를 처방하여 해빙 변화를 조절하는 방법(Lim et al., 2022) 들이 사용된다. 그러나 본 연구는 강제된 해수면 온도가 해빙 모형에 미치는 영향을 분석하고 관련 파라미터의 민감도를 평가하는 것이 목적이므로 ERA5 해수면 온도를 전 지역에 처방하여 모델을 시뮬레이션하였다.

Fig. 2.

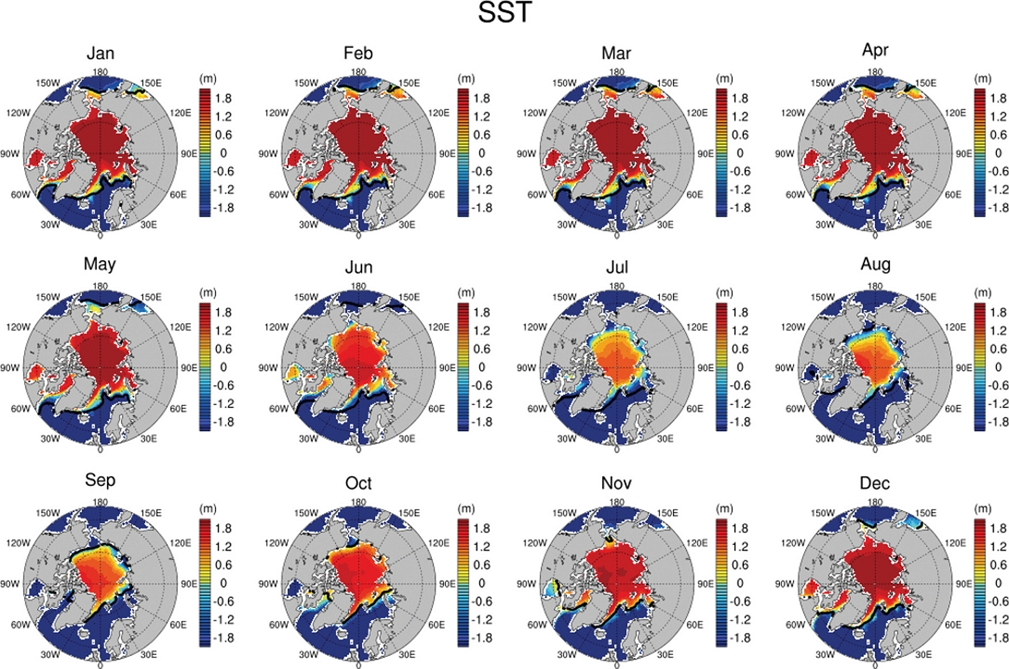
Seasonal SST difference between NOAA OISST and simulated CICE SST (OISST minus CICE) from 1982 to 2018. Black lines indicate that ice extent criteria (ice concentration > 15%).

해빙 면적과 해빙 부피의 계절주기뿐만 아니라 경년변동성도 비교해 보았다(Fig. 3). 해빙 면적은 모형과 모델에서 많이 줄어드는 계절인 북반구 여름철인 7~9 (JAS)월을 분석했다. CICE5와 관측의 여름철 해빙 면적을 살펴보면 0.96의 높은 상관관계를 가진다(Fig. 3a). 1979년부터 2018년까지 지구온난화에 따라서 CICE5와 관측인 NSIDC에서 여름철 해빙 면적이 감소하는 추세를 가지고 있다. 하지만, 모델이 관측에 비해서 해빙 면적을 과대모의하는 경향을 가진다. 모델에서는 여름철 해빙 면적이 10.5 × 10⁶ k m²의 값을 가지고 있는 것에 반해 관측은 1979년에 8.5 × 10⁶ km²로 약 2.0 × 10⁶ k m² 차이를 보이고 있으며 2018년까지 그 차이가 유지되고 있으며 RMSE는 1.9의 값을 가진다.

Fig. 3.

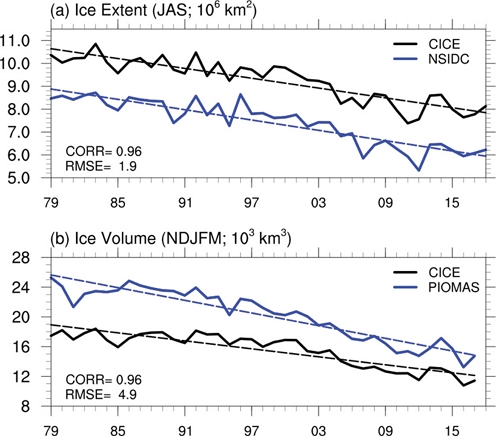
Interannual variability of (a) sea ice extent in summer (JAS) and (b) sea ice volume in winter (NDJFM) of simulated CICE5 using ERA5 atmospheric forcing (black) and observations (blue; sea ice extent from NSIDC and sea ice volume calculated using PIOMAS) from 1979 to 2018. Dotted lines represent the trend over 40 years.

겨울철 해빙 부피의 경우 여름철 해빙 면적과 마찬가지로 모델과 관측에서 모두 감소하는 추세를 보여준다(Fig. 3b). 여름철 해빙면적과는 다르게 CICE5에서 PIOMAS에 비해서 해빙 부피를 과소모의하는 것으로 나타난다. 1979년에서 모델은 17.0 × 10³ k m³의 값을 가지고 있지만 관측은 25.0 × 10³ k m³ 정도로 약 8.0 × 10³ k m³ 차이가 나타난다. 반면, 2018년에는 모델과 관측의 겨울철 해빙 부피의 차이가 4.5 × 10³ km³로 줄어들고 있다. 40년 동안의 경년변동성은 0.96의 높은 상관관계를 가지고 있으며 RMSE는 4.9의 값을 가진다.

해빙 모형의 공간 분포 모의를 진단하기 위해서 여름철과 겨울철의 해빙 농도와 해빙 두께를 분석했다(Fig. 4). 여름철 해빙 농도의 경우 모형은 관측에 비해서 북극해 서반구에서는 과소모의하지만 북극해 대서양 인근과 바렌츠해에서 과대모의 하는 경향이 나타난다(Fig. 4a). 북극해 서반구는 대체로 다년빙(multi-year ice)이 많은 지역으로 여름에도 해빙이 녹지 않고 존재하는 곳이다. 반면 중‧고위도 대서양과 바렌츠해, 베링해와 같은 북극해 주변부는 초년빙(first-year ice)이 많은 지역으로 해빙 면적의 계절변동성을 만드는 중요한 지역이다. CICE5에서 해빙 면적의 계절 변동성을 야기하는 곳인 초년빙 지역의 해빙 농도가 과대모의 되며 이는 모형에서 해빙 면적이 과대모의하는 경향과 일치한다(Figs. 1a and 3a).

Fig. 4.

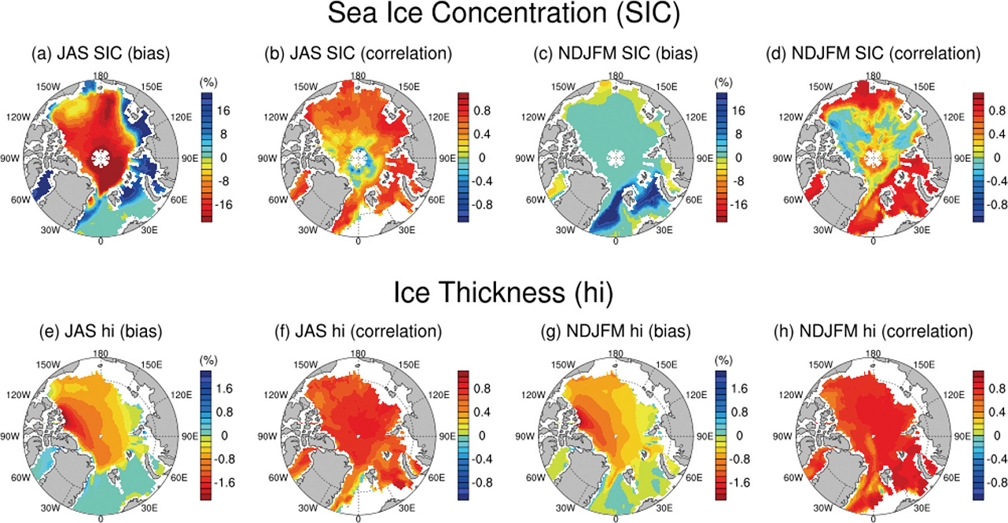
(a, c, e, g) Bias (model minus observation) and (b, d, f, h) correlation between sea ice concentration and sea ice thickness from CICE5 and observations. Top panel shows sea ice concentration and bottom panel shows sea ice thickness. Left panel shows summer season (JAS) and right panel shows winter season (NDJFM). In the observations, sea ice concentration is from NSIDC and sea ice thickness is from PIOMAS. Note that the color bars are reversed in (a, c, e, and g).

ERA5 강제력을 처방한 CICE5에서 겨울철 해빙 농도의 경우 북극해 전 지역에서 과대모의하는 경향이 나타나지만(Fig. 4c) 얼음 두께는 다년빙 지역에서 과소모의한다(Fig. 4g). 겨울철 해빙 부피는 해빙 농도와 해빙 두께의 곱으로 이루어져 있는 것을 고려해본다면 CICE5가 해빙 부피를 과소모의하는 것은(Fig. 3b) 겨울철 해빙 부피에 대해서 해빙 두께의 과소모의 경향이 해빙 농도의 과대모의 경향에 비해 더 큰 영향을 미친다는 것을 의미한다. 해빙 농도와 해빙 두께에 대한 모델과 관측의 패턴 상관 관계를 보면 전체적으로 모형이 관측과 비교해 해빙 농도와 해빙 두께의 공간 분포를 잘 모의 하는 것으로 보이나(Figs. 4b, d, f, and h), 중앙 북극해 부근에서 겨울철 해빙 농도를 잘 모의하지 못하는 것으로 나타난다(Fig. 4d).

3.2 파라미터 민감도 테스트

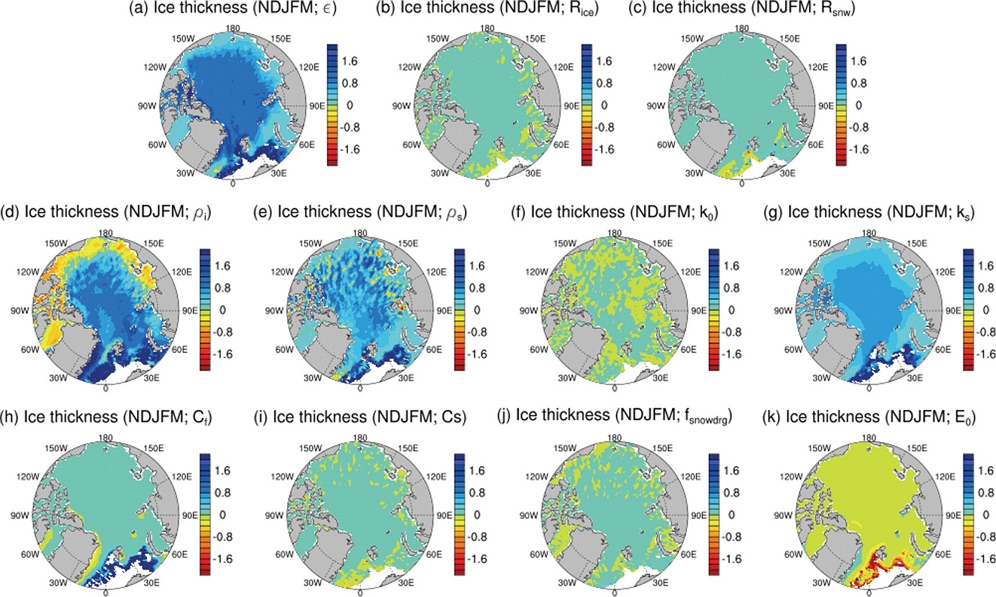
북반구 여름철 해빙 면적에 영향을 주는 해빙 농도에 대해서 파라미터들의 민감도를 보면 방출율을 나타내는 ε와 해빙과 눈의 밀도인 ρ_i와 ρ_s 그리고 눈의 열전도율인 k_s에서 크게 나타나는 것을 알 수 있다(Fig. 5). ε, ρ_i, ρ_s와 k_s에서 모두 북극해 전 지역에서 양의 부호를 가지고 큰 민감도가 나타나는데 이는 파라미터의 값을 늘리면 북극 해빙 농도가 늘어나는 것을 의미한다. 여기서 흡수되는 장파복사의 양을 결정하는 ε는 양의 민감도를 가지며 ε가 커질수록 방출되는 장파복사가 많아져 해빙 농도가 늘어나는 것으로 해석할 수 있다. 해빙 표면의 알베도를 dEdd를 통해 계산하는데 기여하는 파라미터인 R_ice와 R_anow 파라미터 또한 양의 민감도를 가지며 R_ice와 R_anow를 높이면 눈과 얼음의 알베도가 상승해서 해빙 농도가 늘어나는데 기여하는 것으로 판단할 수 있다(Figs. 5a-c). 열역학적 파라미터인 ρ_i, ρ_s, k₀, k_s는 파라미터를 높일수록 해양에서 대기로 빠져나가는 열을 더 방출시켜서 해빙이 녹는 것을 방해함으로써 해빙 농도에 긍정적인 역할을 하는 것으로 판단된다(Figs. 5d-g). 역학적 파라미터들 중에서 해빙 강도(ice strength)를 결정하는 경험적 파라미터인 C_f, 바람 등에 의해서 형석된 빙맥을 표현한 릿징(ridging)과 관련된 C_s와 F_srdg는 그린란드해 부근에서 양의 민감도를 가지지만 EVP (elastic viscous plastic) rheology에서 탄성파의 감쇠를 조절하는 E₀는 음의 민감도를 나타낸다(Figs. 5h-k). C_f는 해빙 강도를 높여 해빙이 외부 강제력에 의해서 쉽게 깨지거나 이동되지 않아 해빙 농도가 높은 상태를 유지하도록 도울 수 있다. C_s가 높아지면 시어 에너지가 릿징에 더 많은 기여를 하며 릿징된 해빙이 많아져 더 두꺼워지고 농도가 높아 질 수 있다. F_srdg가 커지면 눈이 더 많아져서 알베도를 높여 해빙의 농도를 높일 수 있다. 반면, E₀가 커지면 모델이 안정적이게 되며 해빙 역학이 점성 플라스틱에 더 가까워져 현실적인 계산이 될 수 있지만 계산 시간이 늘어나게 되며 너무 큰 값을 줄 경우 바람과 같은 강제력에 대한 반응이 너무 느려질 수 있다. 이 파라미터가 해빙에 주는 직접적인 역할에 대한 해석은 어렵지만 그린란드 해에 대해서는 음의 민감도를 가지는 것을 파악할 수 있다(Fig. 5k). CICE5에서 여름철 북극의 가장자리 부근에서 해빙 농도가 과대모의 되어(Fig. 4a) 여름철 전체 해빙 면적의 계산에서 과대모의되는 경향이 보이는데(Fig. 3a) 이를 해결하기 위해서 ε, ρ_i, ρ_s와 k_s를 줄이면 가장자리 부근에서 해빙 농도가 줄어들 수 있을 것으로 기대된다. 겨울철 북반구 해빙 두께의 경우 해빙 농도와 마찬가지로 ε, ρ_i, ρ_s와 k_s가 큰 민감도를 가지고 있다(Fig. 6). 해빙 농도의 경우 북극해 가장자리 부근에서 큰 민감도를 가지고 있지만 ε, ρ_i, ρ_s, k_s의 경우 북극해 중앙 부근에서도 어느 정도 큰 값을 가지고 있다(Figs. 6a, d, and e).

Fig. 5.

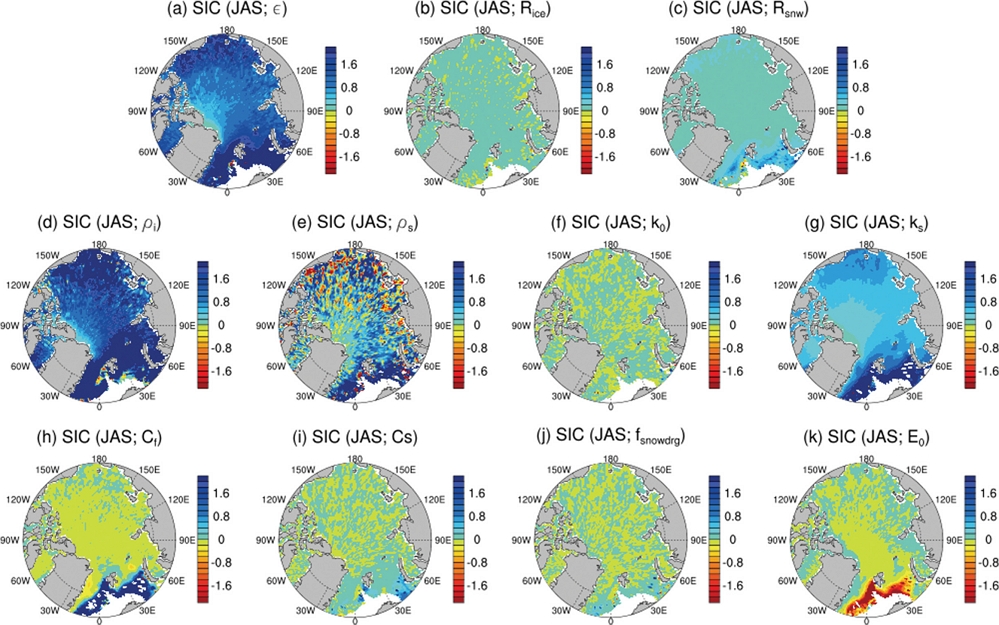
Sensitivity test results of CICE5 parameters (a) ε, (b) Rice, (c) Rsnow, (d) ρi, (e) ρs, (f) k0, (g) ks, (h) Cf, (i) Cs, (j) Fsrdg, and (k) E0 for summer (JAS) sea ice concentration. All results are averaged for 40 years of the differences between experiments with higher parameters and with lower parameters.

Fig. 6.

Same as Fig. 5 except for winter (NDJFM) sea ice thickness.

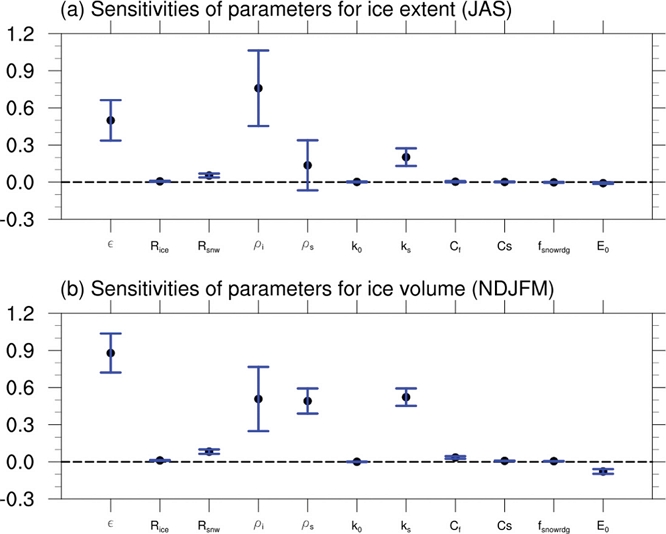
Figure 7a는 여름철 북반구 해빙 면적에 대한 파라미터들의 민감도를 보여준다. 여름철 해빙 면적에 대해서 민감하게 반응하는 파라미터들은 ε, ρ_i, ρ_s, k_s이다. 파라미터의 민감도 부호가 양수이면 파라미터가 증가할수록 북극의 여름철 해빙 면적이 넓어지고 음수이면 줄어드는 것을 의미한다. ERA5 대기 강제력을 이용한 CICE5는 여름철 해빙 면적을 과대모의 하고 있으므로(Fig. 3a) 민감도가 큰 파라미터들 중에서 부호가 양수인 파라미터들을 줄이거나 부호가 음수인 파라미터들을 늘리면 과대모의되는 북반부 해빙 면적이 줄어들 것으로 예상되며 이는 여름철 해빙 농도의 민감도 결과의 공간분포에서 본 결과와 일치한다(Fig. 5). 북극의 겨울철 해빙 부피의 경우도 여름철 해빙 면적과 마찬가지로 ε, ρ_i, ρ_s, k_s 파라미터들이 큰 민감도를 가지고 있다(Fig. 7b). 역학적 과정을 담당하는 파라미터들 중에서 C_f와 E₀는 여름철 해빙 면적보다 겨울철 해빙 부피에 조금 더 큰 민감도를 가지고 있으며 이것으로 보아 역학적 과정을 담당하는 파라미터들은 여름보다는 겨울철에 해빙에 더 큰 영향을 주는 것으로 예상된다. 하지만 이것은 앞의 4개의 파라미터 보다 훨씬 작은 민감도를 보인다. 결과적으로 CICE5에서 여름철 해빙 면적과 겨울철 해빙 부피에 대해서 열역학적 과정에 기여하는 파라미터들(ε, ρ_i, ρ_s, k_s)이 높은 민감도를 가지고 있는 것으로 판단할 수 있다. 여름 해빙 면적에 대해서는 ρ_i가 가장 민감하지만 겨울철 해빙 부피에 대해서는 ε가 가장 민감하게 나타나고 계절에 따라서 민감도의 크기가 달라지는 것을 확인할 수 있다.

Fig. 7.

Parameter sensitivity for (a) summer sea ice extent and (b) winter sea ice volume in CICE5. Vertical bars represent ±1.0 standard deviation over 40 years.

4. 요약 및 결론

본 연구에서는 전 지구 해빙 모형인 CICE5의 해빙 면적과 해빙 부피에 대한 시공간 분포 모의를 검증한 후 물리적 파라미터들에 대한 민감도를 분석했다. CICE5에 ERA5 대기 및 해양 강제력을 처방해 1979년부터 2018년까지 적분한 결과 해빙 면적과 해빙 부피에 대한 계절적인 변동성을 잘 모의하지만 최대값이 나타나는 월이 차이가 나는 것을 확인했다. 또한, 여름철 해빙 면적과 겨울철 해빙 부피의 경우 관측과 재분석 해빙 자료와 비교해 감소 경향과 경년 변동성을 잘 모의하고 있지만 여름철 해빙 면적은 과대모의 하는 경향이 있으며 해빙 부피는 과소모의하는 경향이 나타난다. 이는, ERA5 강제력을 처방한 CICE5가 여름철 해빙 농도를 초년빙이 많은 지역인 북극해 가장자리에서 과대모의하는 것과 다년빙이 많은 지역인 북극해 중앙 부근에서 겨울철 해빙 두께를 과소모의하는 것과 관련이 있다.

파라미터들의 민감도 실험 결과 해빙 표면에서의 장파복사와 알베도 및 해양에서 해빙으로 빠져나가는 열을 조절하는 파라미터들의 민감도는 양수이다. 여름철 해빙 농도에 대해서는 그린란드해와 베링해 지역과 같이 북극해 가장 자리에서 큰 민감도를 가지고 있으며 겨울철 해빙 두께의 경우 북극해 중앙 부근에서 큰 값을 가지고 있다. 해빙의 강도와 릿징, 탄성파의 댐핑 스케일을 조절하는 파라미터들은 작은 민감도를 나타내고 있음을 확인할 수 있다. 여름철 해빙 면적과 겨울철 해빙 부피에 대한 파라미터들의 민감도의 경우 열역학적 파라미터들과 일부 복사 파라미터에서 큰 값을 보이고 있는데 특히 눈과 얼음의 방출율과 얼음 밀도에서 가장 큰 민감도를 보인다. 반면 역학적 과정을 담당하는 파라미터는 작은 값을 가지고 있는 것을 확인 할 수 있다.

그러나, 이 연구에서는 몇 가지 한계가 존재한다. 우선, 현실적인 제약을 고려했을 때 방출율이나 얼음 및 눈의 밀도와 같은 주요 파라미터를 크게 조정하는 것은 현실적으로 어렵다. 이러한 파라미터는 물리적 특성에 따라 제한된 범위 내에서만 조정이 가능하며 방출율의 경우 1.0을 초과할 수 없고, 밀도의 경우도 대기와 해양의 상호작용에 따른 모형의 내부 균형을 고려할 때 큰 변화가 어려운 상황이다. 따라서 모형의 성능을 개선하기 위해서는 이러한 물리적 한계를 감안한 소규모의 조정이 필요하다. 또한, 모델에 적용되는 강제력에 따라 파라미터의 민감도가 달라질 수 있다. 같은 파라미터라도 강제력의 종류나 강도에 따라 그 영향이 다르게 나타날 수 있으며, 이는 특정 모델 설정 하에서만 유효한 결과일 수 있다. 따라서 모델의 설정에 따라 파라미터 민감도 실험 결과를 다르게 해석될 필요가 있다. 그리고, 본 연구에서는 남극을 다루지는 않지만 남극과 북극 지역의 해빙의 바이어스가 다른 경우 남극의 해빙이 증가하도록 모델을 설정할 경우, 북극 해빙이 해빙의 너무 과대모의될 가능성이 존재한다. 마지막으로 해빙 모형이 다른 요소와 결합된 경우 대기-해빙-해양 간의 상호작용으로 인해 모형의 파라미터 민감도 결과가 선형적으로 나오지 않을 수 있다. 예를 들어 본 연구에서는 파라미터 ε가 커지면 해빙 면적이 넓어지고 ε가 작아지면 해빙 면적이 줄어들지만 결합 모델에서는 그렇지 않을 가능성이 존재한다. 따라서 대기-해양 결합 모델에서의 해빙 변동성을 정확하게 모의하려면, 이러한 복잡한 상호작용을 반영할 수 있는 모델의 개선 및 파라미터 실험의 방법 개선 등이 필요하다.

본 연구에서는 CICE5 해빙 모형의 다양한 물리적 파라미터에 대한 민감도 분석을 통해 해빙 모의 성능을 평가하고 개선 방안을 모색하였다. 이 연구의 결과는 해빙 모형의 물리적 파라미터들이 해빙 면적과 해빙 부피에 어떤 영향을 미치는지에 대한 객관적인 정보를 제공하며 파라미터들의 민감도를 정략적으로 제시함으로써 해빙 모형의 성능을 향상시키는 데 기여할 수 있다. 또한 이를 바탕으로 CICE 모형을 포함하고 있는 결합 모델 또는 지구 시스템 모델에서의 기후 예측 성능을 향상시키는데 도움이 되는 원시 정보로 활용될 수 있을 것이다.

Acknowledgments

이 연구는 부산대학교 기본연구지원사업(2년)에 의하여 연구가 수행되었습니다. 본 논문의 개선을 위해 좋은 의견을 제시해 주신 두 분의 심사위원께 감사의 말씀 드립니다.

References

• Bailey, D. A. , M. M. Holland, A . K. DuVivier, E . C. Hunke, and A. K. Turner, 2020: Impact of a new sea ice thermodynamic formulation in the CESM2 sea ice component. J. Adv. Model. Earth Syst., 12, e2020MS002154. [https://doi.org/10.1029/2020MS002154]
• Bouchat, A., and Coauthors, 2022: Sea Ice Rheology Experiment (SIREx): 1. Scaling and statistical properties of Sea-Ice deformation fields. J. Geophys. Res. Oceans, 127, e2021JC017667. [https://doi.org/10.1029/2021JC017667]
• Boutin, G., E. Ólason, P. Rampal, H. Regan, C. Lique, C. Talandier, L. Brodeau, and R. Ricker, 2023: Arctic sea ice mass balance in a new coupled ice-ocean model using a brittle rheology framework. The Cryosphere, 17, 617-638. [https://doi.org/10.5194/tc-17-617-2023]
• Briegleb, B. P., and B. Light, 2007: A delta-Eddington multiple scattering parameterization for solar radiation in the sea ice component of the community climate system model. NCAR Tech. Note NCAR/TN-4721STR, 100 pp.
• Cheddadi, I., P. Saramito, B. Dollet, C. Raufaste, and F. Graner, 2011: Understanding and predicting viscous, elastic, plastic flows. Eur. Phys. J. E, 34, 1-15. [https://doi.org/10.1140/epje/i2011-11001-4]
• Cohen, J., and Coauthors, 2014: Recent Arctic amplification and extreme mid-latitude weather. Nat. Geosci., 7, 627-637. [https://doi.org/10.1038/ngeo2234]
• Cohen, J., and Coauthors, 2020: Divergent consensuses on Arctic amplification influence on midlatitude severe winter weather. Nat. Clim. Change, 10, 20-29. [https://doi.org/10.1038/s41558-019-0662-y]
• Feltham, D. L., N. Untersteiner, J. S. Wettlaufer, and M. G. Worster, 2006: Sea ice is a mushy layer. Geophys. Res. Lett., 33. [https://doi.org/10.1029/2006GL026290]
• Fetterer, F., K. Knowles, W. N. Meier, M. Savoie, and A.K . Windnagel, 2017: Sea ice index. version 3. National Snow and Ice Data Center. [https://doi.org/10.7265/N5K072F8]
• Francis, J. A., and S. J. Vavrus, 2012: Evidence linking Arctic amplification to extreme weather in mid-latitudes. Geophys. Res. Lett., 39, L06801. [https://doi.org/10.1029/2012GL051000]
• Guemas, V., F. J. Doblas-Reyes, K. Mogensen, S. Keeley, and Y. Tang, 2014: Ensemble of sea ice initial conditions for interannual climate predictions. Climate Dyn., 43, 2813-2829. [https://doi.org/10.1007/s00382-014-2095-7]
• He, S., Y. Gao, F. Li, H. Wang, and Y. He, 2017: Impact of Arctic Oscillation on the East Asian climate: A review. Earth-Sci. Rev., 164, 48-62. [https://doi.org/10.1016/j.earscirev.2016.10.014]
• Hersbach, H., and Coauthors, 2020: The ERA5 global reanalysis. Quart. J. Roy. Meteor. Soc., 146, 1999-2049. [https://doi.org/10.1002/qj.3803]
• Hunke, E. C., and J. K. Dukowicz, 2002: The Elastic-Viscous-Plastic sea ice dynamics model in general orthogonal curvilinear coordinates on a Sphere—Incorporation of metric Terms. Mon. Wea. Rev., 130, 1848-1865. [https://doi.org/10.1175/1520-0493(2002)130<1848:TEVPSI>2.0.CO;2]
• Hunke, E. C., D. Notz, A. K. Turner, and M. Vancoppenolle, 2011: The multiphase physics of sea ice: a review for model developers. The Cryosphere, 5, 989-1009. [https://doi.org/10.5194/tc-5-989-2011]
• Hunke, E. C., W. H. Lipscomb, A. K. Turner, N. Jeffery, and S. Elliott, 2015: CICE: The Los Alamos Sea Ice Model documentation and software user’s manual version 5.1. Los Alamos National Laboratory Doc. LA-CC-06-012, 116 pp.
• Kim, B.-M., S.-W. Son, S.-K. Min, J.-H. Jeong, S.-J. Kim, X. Zhang, T. Shim, and J . -H. Yoon, 2014: Weakening of the stratospheric polar vortex by Arctic sea-ice loss. Nat. Commun., 5, 4646. [https://doi.org/10.1038/ncomms5646]
• Kim, S.-H., H.-J. Sung, S.-J. Kim, E.-H. Baek, J.-Y. Moon, and B.-M. Kim, 2022: Contribution of ural and kamchatka blockings to the amplified warm Arctic-Cold Eurasia pattern under Arctic Sea Ice Loss and Eurasian cooling. J. Climate, 35, 4071-4083. [https://doi.org/10.1175/JCLI-D-21-0635.1]
• Kug, J.-S., J.-H. Jeong, Y.-S. Jang, B.-M. Kim, C. K. Folland, S.-K. Min, and S.-W. Son, 2015: Two distinct influences of Arctic warming on cold winters over North America and East Asia. Nature Geosci., 8, 759-762. [https://doi.org/10.1038/ngeo2517]
• Lee, S-B., and J.-B. Ahn, 2014: Sensitivity study of simulated sea-ice concentration and thickness using a global sea-ice model (CICE). Atmosphere, 24, 555-563. [https://doi.org/10.14191/Atmos.2014.24.4.555(inKoreanwithEnglishabstract)]
• Lim, W.-I., H.-S. Park, A. L. Stewart, and K.-H. Seo, 2022: Suppression of Arctic sea ice growth in the Eurasian-Pacific seas by winter clouds and snowfall. J. Climate, 35, 669-686. [https://doi.org/10.1175/JCLI-D-21-0282.1]
• Lipscomb, W. H., 2001: Remapping the thickness distribution in sea ice models. J. Geophys. Res. Oceans, 106, 13989-14000. [https://doi.org/10.1029/2000JC000518]
• Lipscomb, W. H., and E. C. Hunke, 2004: Modeling Sea Ice Transport Using Incremental Remapping. Mon. Wea. Rev., 132, 1341-1354. [https://doi.org/10.1175/1520-0493(2004)132<1341:MSITUI>2.0.CO;2]
• Mu, L., and Coauthors, 2020: Toward a data assimilation system for seamless sea ice prediction based on the AWI climate model. J. Adv. Model. Earth Syst., 12, e2019MS001937. [https://doi.org/10.1029/2019MS001937]
• Reynolds, R. W., T. M. Smith, C. Liu, D. B. Chelton, K. S. Casey, a nd M . G. Schlax, 2007: Daily high-resolution-blended analyses for sea surface temperature. J. Climate, 20, 5473-5496. [https://doi.org/10.1175/2007JCLI1824.1]
• Ricker, R., S. Hendricks, F. Girard-Ardhuin, L. Kaleschke, C. Lique, X. Tian-Kunze, M. Nicolaus, and T. Krumpen, 2017: Satellite-observed drop of Arctic sea ice growth in winter 2015~2016. Geophys. Res. Lett., 44, 3236-3245. [https://doi.org/10.1002/2016GL072244]
• Stroeve, J. C., D. Schroder, M. Tsamados, and D. Feltham, 2018: Warm winter, thin ice? The Cryosphere, 12, 1791-1809. [https://doi.org/10.5194/tc-12-1791-2018]
• Sun, L., C. Deser, R. A. Tomas, and M. Alexander, 2020: Global coupled climate response to polar sea ice loss: Evaluating the effectiveness of different ice-constraining approaches. Geophys. Res. Lett., 47, e2019GL085788. [https://doi.org/10.1029/2019GL085788]
• Sun, S., and A. Solomon, 2024: Suitability of the CICE sea ice model for seasonal prediction and positive impact of CryoSat-2 ice thickness initialization. The Cryosphere, 18, 3033-3048. [https://doi.org/10.5194/tc-18-3033-2024]
• Turner, A. K., and E. C. Hunke, 2015: Impacts of a mushy-layer thermodynamic approach in global sea-ice simulations using the CICE sea-ice model. J. Geophys. Res. Oceans, 120, 1253-1275. [https://doi.org/10.1002/2014JC010358]
• Turner, A. K., E. C. Hunke, and C. M. Bitz, 2013: Two modes of sea-ice gravity drainage: A parameterization for large-scale modeling. J. Geophys. Res. Oceans, 118, 2279-2294. [https://doi.org/10.1002/jgrc.20171]
• Vihma, T., 2014: Effects of Arctic sea ice decline on weather and climate: A Review. Surv. Geophys., 35, 1175-1214. [https://doi.org/10.1007/s10712-014-9284-0]
• Walsh, J. E., 2014: Intensified warming of the Arctic: Causes and impacts on middle latitudes. Global Planet. Change, 117, 52-63. [https://doi.org/10.1016/j.gloplacha.2014.03.003]
• Wu, Q., L. Cheng, D. Chan, Y. Yao, H. Hu, and Y. Yao, 2016: Suppressed midlatitude summer atmospheric warming by Arctic sea ice loss during 1979~2012. Geophys. Res. Lett., 43, 2792-2800. [https://doi.org/10.1002/2016GL068059]
• Xu, X., S. He, Y. Gao, B. Zhou, and H. Wang, 2021: Contributors to linkage between Arctic warming and East Asian winter climate. Climate Dyn., 57, 2543-2555. [https://doi.org/10.1007/s00382-021-05820-x]
• Yadav, J . , A. Kumar, a nd R . Mohan, 2020: D ramatic decline of Arctic sea ice linked to global warming. Nat. Hazards, 103, 2617-2621. [https://doi.org/10.1007/s11069-020-04064-y]
• Yang, C.-Y., J. Liu, and S. Xu, 2020: Seasonal Arctic sea ice prediction using a newly developed fully coupled regional model with the assimilation of satellite sea ice observations. J. Adv. Model. Earth Syst., 12, e2019MS001938. [https://doi.org/10.1029/2019MS001938]
• Zhang, C., X. Chen, and S. Ji, 2022: Semantic image segmentation for sea ice parameters recognition using deep convolutional neural networks. Int. J. Appl. Earth Obs. Geoinformation, 112, 102885. [https://doi.org/10.1016/j.jag.2022.102885]
• Zhang, J., 2021: Sea ice properties in high-resolution sea ice models. J. Geophys. Res. Oceans, 126, e2020-JC016686. [https://doi.org/10.1029/2020JC016686]
• Zhang, J., and D. A. Rothrock, 2003: Modeling Global Sea Ice with a thickness and enthalpy distribution model in generalized curvilinear coordinates. Mon. Wea. Rev., 131, 845-861. [https://doi.org/10.1175/1520-0493(2003)131<0845:MGSIWA>2.0.CO;2]