한반도 상층의 5년간(2019~2023) 항공 난류 관측자료 분석 및 예측모델(KTG와 GKTG) 성능 평가
Ⓒ 2025 Korean Meteorological Society
Abstract
This study conducted a statistical analysis of turbulence events using in-situ eddy dissipation rate (EDR) observation data collected above 20,000 feet over the Korean Peninsula from 2019 to 2023. Additionally, the performances of two operational turbulence prediction models from the Korea Aviation Meteorological Office, which are the Korean Aviation Turbulence Guidance (KTG) and Global KTG (GKTG) systems, were evaluated against the same insitu EDR observations. The verification process employed the probability of detection (POD) method, allowing for an objective assessment of prediction accuracy. The statistical analysis results of in-situ EDR data revealed that data was primarily collected along flight routes, with observations increasing over time. The moderate-or-greater (MOG) turbulence was observed frequently during the daytime, and was most prevalent in spring. The comparison of the characteristics of PIREP and in-situ EDR observations showed similar seasonal trends. The evaluation results compared with these EDR data showed both KTG and GKTG demonstrated performance levels applicable for aviation industry professionals (0.809 and 0.805 respectively). Accuracy at the MOG threshold was evaluated by analyzing the correlation between the area under the curve (AUC) and true skill statistic (TSS) values. The KTG model showed relatively higher accuracy. Based on these results, model improvements were implemented, enhancing the TSS of GKTG by 0.22 through threshold adjustment. Considering that models currently used by the Korea Aviation Meteorological Office mainly focus on predicting clear air turbulence and mountain wave turbulence, future research should aim to improve prediction capabilities for convectively-induced and near-cloud turbulence.
Keywords:
Aviation turbulence, EDR, Evaluation, KTG, GKTG1. 서 론
항공 난류(Aviation Turbulence)는 수십 m에서 수천 m의 수평 규모로 발생하여 운항 중인 항공기에 직접적인 영향을 끼치는 대기 중 요란운동으로 정의되며, 예기치 못하게 강한 강도로 조우했을 경우 물리적 및 경제적인 피해가 야기될 수 있다(Lester, 1994; Sharman et al., 2012; Sharman and Lane, 2016; Sharman and Pearson, 2017). 이러한 항공 난류가 발생할 수 있는 대표적인 요인으로는 제트기류, 상층전선, 산악파, 대류시스템 등이 있다(Lane et al., 2012; Sharman and Lane, 2016). 이와 같은 항공 난류 발생 요인들은 개별적으로 작용할 수도 있지만, 복합적으로 작용하여 난류를 생성하는 경우가 많다.
대부분의 항공 난류 관련 사고는 10,000 ft 고도 이상의 자유대기에서 순항하는 항공기에서 많이 경험되고 피해가 보고되었다(Sharman et al., 2006; Kim and Chun, 2011; Lee and Chun, 2015). 자유대기에서 생성되는 항공 난류 중 구름이 없거나 층운형의 얇은 구름만 존재하는 맑은 하늘에서 급작스럽게 발생하여 육안 또는 비행기에 탑재된 레이더로 감지할 수 없는 난류를 청천난류(Clear-Air Turbulence; CAT)라고 한다(Chambers, 1955; Lester, 1994; Sharman et al., 2006; Kim et al., 2011). 특히, 강한 강도의 CAT을 조우하게 되면 예상하지 못한 사고로 이어져 큰 피해를 입을 가능성이 크다. 따라서 안정적이고 경제적인 항행을 위해서는 순항고도에서의 정확한 항공 난류 예측이 필요하다.
하지만 항공 난류는 작은 규모와 짧은 지속시간으로 인하여 현재의 수치예측모델에서 직접 예측 자료를 산출하는 것은 어렵다. 따라서 현대 대부분의 항공 난류의 예측은 대규모 난류에너지가 항공기에 영향을 미칠 수 있는 소규모의 에디로 캐스케이드 다운(cascade down)한다는 가정을 가지고, 수치모델에서 모의될 수 있는 난류 발생 관련 큰 규모의 대기운동을 진단하는 지수들을 활용한 항공 난류 예측 모델 개발 및 예보에서의 활용이 이루어지고 있다(Dutton and Panofsky, 1970; Cho and Lindborg, 2001; Tung and Orlando, 2003; Sharman et al., 2006). 개발된 대부분의 항공 난류 예측모델들은 CAT 진단지수들만을 활용하여 만들어졌으나(Sharman et al., 2006; Kim and Chun, 2011; Lee and Chun, 2018), 최근에는 구름 주변 난류(Near Cloud Turbulence; NCT) 및 산악파 난류(Mountain Wave Turbulence; MWT)에 대한 진단지수 및 이를 포함한 난류 예측모델 개발이 이루어지고 있다(Sharman and Pearson, 2017; Kim et al., 2021).
한국을 포함한 동아시아 지역은 기후학적으로 전세계에서 가장 강한 제트기류가 나타나는 지역으로 알려져 있다(Koch et al., 2006; Jaeger and Sprenger, 2007; Lee et al., 2023). 그리고, 한국은 지형적으로 산악지역이 많아 산악파가 발생하기 쉬운 조건을 가지고 있다(Kim and Chun, 2011). 그러므로, 한반도에서의 항공 난류 발생가능성은 매우 높다. 이에, 기상청(Korea Meteorological Administration; KMA)에서는 미국 국립기상연구소(National Center for Atmospheric Research; NCAR)의 항공 난류 예측 모델인 Graphical Turbulence Guidance (GTG) 시스템(Sharman et al., 2006; Sharman and Pearson, 2017)을 기반으로 하여 개발된 동아시아 영역에 대한 한국형 항공 난류 예측모델(Korean aviation Turbulence Guidance, KTG)과 전지구 영역에 대한 한국형 항공 난류 예측모델(Global-Korean aviation Turbulence Guidance; GKTG)을 현업으로 운영하여 항공 난류를 일 4회(0000, 0600, 1200, 1800 UTC) 예보하고 있다.
한국 상층에서 발생하는 난류를 더 잘 이해하고 예측하기 위해서는 한반도 상층 난류의 시·공간적 통계분석 및 예측 모델에 대한 검증을 수행하는 것이 중요하다. 그러나, 현재 한반도에 초점을 맞춘 in-situ Eddy Dissipation Rate (EDR) 관측에 대한 통계 분석이 부족하며, 기상청에서 현업 예보에 활용되고있는 난류 예측모델(KTG, GKTG)에 대한 지속적이고 장기적인 검증 수행 및 개선이 필수적이다.
따라서, 본 연구에서는 먼저 국제항공운송협회(International Air Transport Association; IATA)에 수집된 in-situ EDR 관측자료를 사용하여 2019년부터 2023년까지 한반도 상층(20,000 ft 이상)에서 발생한 항공 난류에 대한 전체 기간, 연도, 계절, 월, 시간 및 고도별 통계분석을 진행하였다. 다음으로 in-situ EDR 관측자료와 난류 예측자료(KTG, GKTG)를 비교하여 현업 항공 난류 예측모델의 성능을 평가하였고 개선 방안에 대해 논하였다.
2. 자료 및 검증 방법
2.1 관측자료
EDR은 inertial subrange 내에서 점성 효과에 의해 난류 에너지가 열로 변환되는 속도를 나타내는 에너지 소산율(ε)의 1/3제곱을 나타내며, 대기 난류 강도를 추정하는 유용한 척도로 알려져 있다(Cornman et al., 1995; Sharman et al., 2014). 또한, 국제민간항공기구(International Civil Aviation Organization; ICAO)에서 지정한 표준 항공 난류 지표이다.
한반도 상공에 나타나는 항공 난류에 대한 시·공간적 통계분석 및 실시간 관측자료와의 비교를 통한 항공 난류 예측자료(KTG와 G K TG) 검증을 위해, 2019년 1월 1일부터 2023년 12월 31일까지의 총 5년 기간 동안 국제항공운송협회(IATA)에 수집된 민간 항공기에서 관측한 in-situ EDR 자료를 사용하였다(Fig. 1). 전체 자료의 총 관측자료수는 140,215,485개였으며, 2019년부터 2023년까지 순서대로 각각 22,737,220개, 21,221,601개, 27,067,457개, 30,906,672개, 38,282,535개로 연도별로 관측자료수가 증가하는 경향성을 보였다.
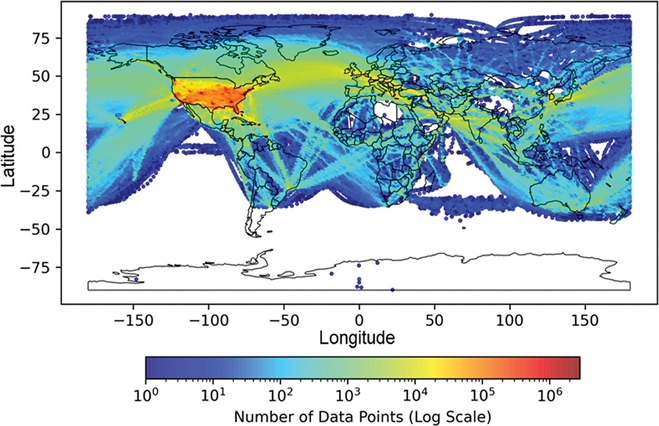
Horizontal distribution of IATA flight data at all altitudes accumulated within a 1o × 1o horizontal grid box for 5 years (2019~2023).
본 연구에서는 한반도 영역(27.5~44oN, 119~135oE)에 대해서 검증을 수행하였으며, 고도는 CAT가 주로 발생하는 고도인 상층 항공 난류 검증에 초점을 맞추기 위해 고도 20,000 ft 이상의 관측자료를 사용하였다.
관측자료의 항공 난류 강도 임곗값은 선행연구(Sharman et al., 2014; Sharman and Pearson, 2017; Lee and Chun, 2018; Lee et al., 2022)를 참고하여 null (NIL), light (LGT), moderate (MOD), severe (SEV)를 각각 EDR < 0.15 m2/3 s-1, 0.15 m2/3 s-1 ≤ EDR < 0.22 m2/3 s-1, 0.22 m2/3 s-1 ≤ EDR < 0.34 m2/3 s-1 0.34 m2/3 s-1 ≤ EDR로 분류하였다.
2.2 한국형 항공 난류 예측모델(KTG)
KTG 모델은 동아시아영역 CAT 예측을 목적으로 동아시아 영역에서 관측된 조종사 보고(PIlot REPorts; PIREPs) 난류 자료 및 기상청 현업 수치기상모델을 사용하여 미국의 GTG2 (GTG version 2) 모델의 방법론(Sharman et al., 2006)을 기반으로 개발되었다(Kim and Chun, 2011). 자세한 항공난류 예측모델의 설명은 Kim and Chun (2011, 2012)에서 다뤄졌다. 간략하게 설명하면, 첫 번째로 기상청 현업 수치기상모델에서 산출되는 난류 관련 지수들(여기서는 20개)과 관측자료를 비교하여 각각의 지수들에 대해 각 난류강도에 대응되는 임곗값들 및 난류 예측성 정보에 대한 Look-up table을 만든다. 다음으로 Table 1로 만든 각 개별 난류 진단지수들의 임곗값들을 각 난류 강도 구간별 1차원 mapping 함수에 적용하여 0부터 1사이의 값으로 개별지수들을 변환하여 다양한 단위 및 범위를 가지는 개별난류 지수값들을 표준화한다. 마지막으로 mapping된 개별지수들에 대해서 가중치를 적용한 후, 하나로 결합하여 최종 K TG 난류 지수 값을 산출한다. 여기서, KTG의 난류강도 임곗값은 단위가 없고 LGT, MOD, SEV가 각각 0.3, 0.475, 0.75로 제시되었다. KTG는 동아시아 영역에서 하루 4회(0000, 0600, 1200, 1800 UTC) 30시간 예측 시간까지 3시간 간격으로 예측하고 있으며, 고도는 지상∼40,000 ft에 대해서 1,000 ft 간격으로 12 km 수평 해상도의 항공난류 예측자료를 산출하고 있다.
KTG는 기상청 현업 통합모델(Unified Model; UM)의 지역 예보모델(Regional Data Assimilation and Prediction System; RDAPS)을 기반으로 개발되었다. 하지만, 2019년 4월부터 RDAPS 운영이 종료되면서, 10 km 수평 해상도를 가지는 UM 전지구 예보모델(Global Data Assimilation Prediction System, GDAPS)자료를 12 km 수평 해상도 자료로 변환하여 K TG를 운영하고 있다. 따라서, 본 연구에서는 2019년 1월부터 3월까지의 KTG 예측 자료는 검증에서 제외하고 GDAPS 기반의 KTG 예측 자료를 검증에 사용하였다.
2.3 전지구 한국형 항공 난류 예측모델(GKTG)
GKTG 모델은 국제선 운행의 급격한 증가에 따른 전지구적인 항공 난류 예보의 필요성에 인하여, 전지구 영역 난류 예측을 위해 GTG3 (GTG version3) 모델의 방법론(Sharman and Pearson, 2017)을 기반으로 한국 기상청 현업 수치기상모델에 맞추어 개발되었다(Lee and Chun, 2018). 그리고 K TG에서는 CAT 지수만이 고려되었으나, GKTG는 MWT도 함께 고려되어 항공 난류가 예측되어진다.
구체적인 내용은 Lee and Chun (2018)에 서술되어 있으며, 여기에서는 간략하게 설명하겠다. 먼저, 기상청 현업 수치기상모델에서 산출된 변수들을 이용하여 다양한 CAT 및 MWT 관련 진단지수들을 계산한다. KTG의 경우, 앞서 언급했듯이 계산된 진단지수들을 0에서 1사이의 값으로 표준화하여 하나로 결합하는 방법으로 계산된다. 한편, GKTG의 경우, 계산된 진단지수들의 다양한 값의 범위 및 단위들을 지수별 EDR 전환식을 이용하여 EDR 규모로 표준화 한 후, 결합하여 하나의 통합난류 예측지수인 G K TG 난류지수 값을 CAT 및 MWT 각각에 대해 산출한다. 또한 각 격자점에서 CAT-GKTG와 MWT-GK TG 중 더 큰 난류 값을 반영하여 산출한 MAX (maximum GKTG)자료도 함께 산출된다. 여기서, EDR로 산출되는 G K TG 예측 정보의 난류 강도별 임곗값은 LGT, MOD, SEV가 각각 0.15, 0.22, 0.34 m2/3 s-1로 제시되었다. GKTG는 KTG와 동일하게 UM GDAPS에서 산출된 기상변수들을 이용하지만, UM GDAPS의 수평 해상도(10 km) 그대로 계산된다. 하루 4회(0000, 0600 1200, 1800 UTC) 36시간 예측 시간까지 3시간 간격으로 생산되고, 지상으로부터 41,000 ft까지 1,000 ft 간격의 고도로 항공 난류 예측자료를 산출하고 있다. GKTG는 3가지의 난류(CAT, MWT, MAX)를 생산하지만, 관측된 자료에서 난류의 종류를 정확히 구분할 수 없으므로 검증 시에는 모든 경우를 포함한 MAX 자료를 이용하여 검증을 진행하였다.
2.4 검증 방법
본 연구에서 POD (Probability Of Detection) 통계적 검증 방법(Mason, 1982)을 사용하여 검증하였다. POD 방법을 통해 구해지는 PODY (Probability Of Detection of “Yes”)는 중강도 이상(Moderate-Or-Greater MOG)의 난류가 관측된 지점에서 난류예측정보가 난류를 예측할 확률을, PODN (Probability Of Detection of “No”)은 NIL이 관측된 지점에서 난류예측정보 역시 난류를 예측하지 않을 확률을 나타낸다(Sharman et al., 2006; Kim et al., 2011).
PODY는 식(1)으로 계산된다. 여기서 TP (True Positive)는 실제 MOG 난류가 발생한 사건을 모델이 정확히 예측한 수이고, FN (False Negative)는 실제 MOG 난류가 발생했으나 모델이 예측하지 못한 수이다. PODN은 식(2)으로 계산된다. TN (True Negative)은 실제 NIL 사건을 모델이 정확히 예측한 수이고, FP (False Positive)는 실제 NIL 사건을 모델이 잘못 예측한 수이다(Sharman and Pearson, 2017; Kim et al. 2018).
이러한 지표들을 산출하기 위해, MOG (NIL)가 관측된 지역과 가장 근접한 격자점에서 난류 예측값이 주어진 임의의 임곗값을 넘는(넘지 않는) 경우를 계산한다(Kim and Chun, 2012; Lee and Chun, 2018). 이 과정을 여러 임곗값에 대해 반복하여 PODY와 PODN 값들을 얻으며, 이를 통해 ROC (Receiver Operating Characteristic) 곡선이 그려지고 곡선 아래 면적인 AUC (Area Under the Curve)를 계산할 수 있다(Sharman et al., 2006; Gill and Buchanan, 2014; Storer et al., 2019). 이 AUC가 모델의 성능을 나타낸다(Fielding and Bell, 1997).
ROC 곡선과 AUC는 이진 분류 모델의 성능을 평가하는 데 유용한 도구로, 특히 불균형한 데이터셋에서도 안정적으로 모델 성능을 평가할 수 있다(Tebaldi et al., 2002; Kim et al., 2021).
| (1) |
| (2) |
TSS (True Skill Statistic)는 이진 예측의 정확도를 평가하는 또 다른 중요한 지표로 일기예보의 정확성을 평가하는 데 많이 사용되어왔다(Allouche et al., 2006). TSS는 PODY와 PODN을 사용하여 계산되며 다음과 같이 정의된다:
| (3) |
AUC는 0.5에서 1사이의 범위를, TSS는 –1에서 +1 사이의 범위의 값을 가지며 두 값 모두 1에 가까울수록 예측 성능이 우수함을 의미한다. 반면, AUC는 0.5, TSS는 0 이하로 내려갈수록 예측성능이 매우 낮고 무작위 추측과 동일한 예측성능을 갖는 것으로 해석할 수 있다(Gill and Buchanan, 2014; Kim et al., 2018). AUC는 예측모델의 전반적인 분류 능력을 평가하는 반면, TSS는 특정 임곗값에 대한 예측능력을 정량화 한다(Allouche et al., 2006; Belo, 2015). 이렇게 TSS와 함께 ROC 곡선 및 AUC를 동시에 고려함으로써, 모델의 예측 성능을 다각도로 분석하고 평가할 수 있다(Allouche et al., 2006; Sharman et al., 2006; Kim et al., 2021).
본 연구에서는 2019년부터 2023년까지의 총 5년간 상층(20,000 ft 이상)의 한반도 영역(27.5~44oN, 119~135oE)에 대해 항공난류 예측모델 검증을 진행하였다. 특히, MOG 난류에 대한 예측이 잘 이루어졌는지 살펴보기 위해 MOG 난류 관측자료(0.22 m2/3 s-1 ≤ EDR)와 NIL 난류 관측자료(EDR < 0.01 m2/3 s-1)를 사용하여 검증하였다. 기존 NIL 강도의 난류는 EDR < 0.15 m2/3 s-1이지만, 반복적인 NIL 난류 사례를 줄이기 위해 더 낮은 EDR 임곗값인 EDR < 0.01 m2/3 s-1을 사용하였다(e.g. Kim et al., 2018; Lee et al., 2022). 예측자료는 0000 UTC에 생산되는 K TG와 GKTG 자료를 사용하였으며, 예측 시간(Forecast Time) 별로 검증을 진행하였다. 즉, 0000 UTC에 생산되는 3시간 간격의 0000~+2100 UTC 예측자료를 사용하여 각 예측 시간마다 검증을 진행하였다.
검증은 예측 시간으로부터 ±2시간 내의 관측자료를 사용하였다(e.g. Kim et al., 2011). 또한 해당 시간 및 격자점 내에 중복된 관측자료가 있는 경우, 관측된 자료 중 가장 큰 EDR 값을 사용함으로써 중복된 자료를 제거한 후 검증에 사용하였다.
3. 결 과
3.1 In-situ EDR 관측자료 통계분석
2019년부터 2023년까지 IATA에서 수집한 20,000 ft 이상에서 관측된 in-situ EDR의 수평분포도를 Fig. 2a에 나타내었으며, MOG 난류 관측 빈도 수평분포도를 Fig. 2b에 나타내었다. 여기서, Fig. 2b는 0.2도 수평 그리드에 대하여 MOG 난류 관측 누적 빈도수를 나타내었다.
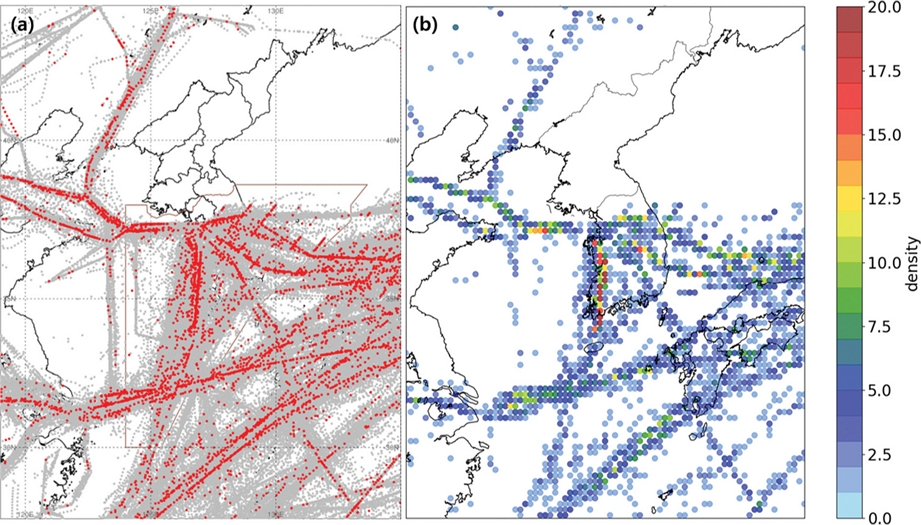
(a) Distribution of in-situ EDR observations for the entire period (gray) and distribution of observations at or above MOG (red), (b) frequency distribution of in-situ EDR observations at or above MOG based on a 0.2-degree horizontal grid.
EDR은 대부분 항공로를 따라 관측되었다. 5년간 총 관측자료수는 418,099개, 각 강도별로는 NIL 398,287개, LGT 15,306개, MOD 4,039개, SEV 467개로 나타났다. 강도별 관측 비율은 NIL 95.26%, LGT 3.66%, MOD 0.97%, SEV 0.11%로 강도가 높아질수록 관측자료수가 확연히 감소하는 것을 확인하였다. Figure 2b를 살펴보면, MOG 강도 난류는 김포-제주를 지나는 노선에서 주로 관측이 되었다. 또한, 위도 35~40oN 사이에서도 MOG 강도의 난류 관측이 자주 이루어진 것으로 보인다.
다음으로는 연도별, 계절별, 시간별 그리고 고도별로 EDR 관측자료 통계분석을 진행하였다.
2019년부터 2023년까지 연도별 관측자료는 순서대로 37,128개, 58,649개, 77,011개, 72,070개, 173,241개로, 2022년에 약간 감소하였지만 전반적으로 관측자료가 증가하는 추세를 보였다. 이는 Miyamoto et al. (2023) 연구결과와 일치하였으며, 그들은 항공기 운항수 증가가 관측자료수의 증가에도 기여했음을 보고하였다.
강도별 EDR 관측자료의 추세도 유사한 경향을 보였으며, 특징적으로 2023년에 NIL 난류 관측자료수가 급격하게 증가하였다(Fig. 3). MOG 난류 관측 자료수는 매년 증가하는 경향을 보인다. 하지만, MOG 난류 관측 비율은 2019년 약 1.7%에서 2023년 1% 미만으로 지속적으로 감소했다. 대기 중 난류 발생량의 증가는 선행연구에서도 보고되었으며(Storer et al., 2017; Williams, 2017; Lee et al., 2019; Tenenbaum et al., 2022), MOG 난류 관측 비율이 감소하는 것은 시간이 지남에 따라 전반적인 항공 운항 증가에 따른 MOG 난류에 대한 예측 및 회피 능력이 향상되고 있음을 시사할 수 있다(Sharman et al., 2006; Kim et al., 2009; Sharman and Pearson, 2017; Lee et al., 2022).
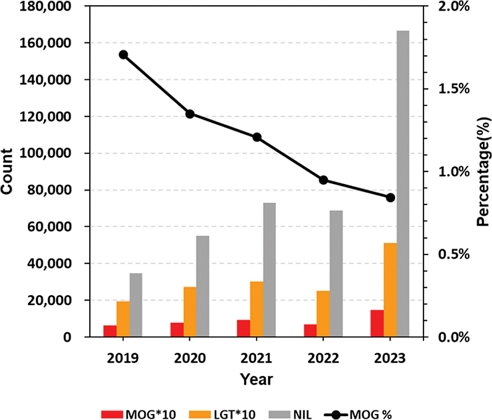
Annual number of observations by intensity and percentage of MOG observations (bar graph and line graph, respectively).
Figure 4은 5년간의 월별 NIL, LGT, MOG 난류 관측자료수와 MOG 관측 비율을 보여준다. 먼저, 계절별로 살펴보면, 총 관측자료수는 가을(September-October-November, SON)에 116,593개로 가장 많았으며 순서대로 여름(June-July-August; JJA)에 114,240개, 봄(March-April-May; MAM)에 96,580개, 겨울(December-January-February; DJF)에 90,677개로 많이 나타났다. LGT 및 MOG 난류 관측자료수는 경향성이 유사했으며 여름, 봄, 가을, 겨울 순으로 많았다. MOG 난류 관측 비율은 봄(4.01%), 여름(3.89%), 가을(2.42%), 겨울(2.36%) 순으로 높았다. 이러한 MOG 난류 관측 비율의 결과는 선행연구와 유사하게 나타났다(Lee and Chun, 2015).
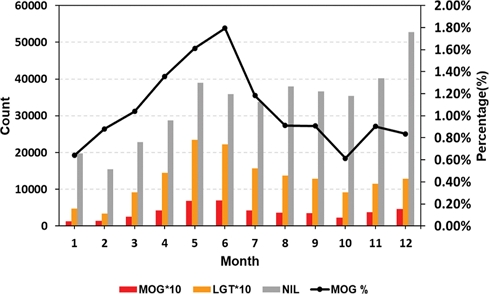
Monthly number of observations by intensity and percentage of MOG observations (bar graph and line graph, respectively).
좀 더 구체적으로 살펴보면, 총 관측자료수는 12월에 54,482개로 가장 많았으며 다음으로 5월(41983개)과 11월(41769개)에 많았다. 그리고 2월에 15,907개로 가장 적은 관측자료수를 보였다. LGT 및 MOG 난류 관측자료수는 5월과 6월에 가장 높은 빈도를 보였고 겨울철에 상대적으로 낮았다. MOG 난류 관측 비율은 0.61~1.79% 범위에서 변동하였으며, 6월에 최고, 10월에 최저를 기록했다.
위와 같은 난류의 계절 및 월별 특성이 나타나는 이유로, Lee and Chun (2015)와 Kim and Chun (2011)은 한반도 및 동아시아 영역에서 봄과 겨울에는 강한 제트기류로 인한 연직바람시어(Vertical Wind Shear; VWS)의 증가가 항공 난류 발생의 주요 원인이 되며, 여름철에는 장마 전선 활성화와 태풍 등 중규모 대류계의 발달로 인한 강한 대류시스템이 항공 난류 발생에 영향을 끼친 것으로 분석하였다.
더 나아가 시간에 따른 관측자료수를 살펴보면(Fig. 5), 총 관측자료수는 0000 UTC부터 관측자료수가 증가하다가 0500 UTC에 최고(32,754개)에 도달한 후 점차 줄어들어 1800 UTC에 최저(7,576개)에 도달한 후 다시 증가하는 경향을 보였다. 난류 강도별로 살펴보면 LGT 및 MOG 난류 관측자료수도 주로 낮에 높게 나타나, 총 관측자료수와 유사한 경향성을 보였다. MOG 난류 관측 비율은 시간대 별로 변동이 있었으나, 크지는 않았다. 주로 낮에 특징적으로 1300 UTC에 1.50%로 가장 높았는데, 자세히 살펴보니 주로 제주도보다 더 남쪽의 상공에서 지나가는 항공기에서 주로 관측이 되었으며, 김포-제주를 지나는 노선에서도 종종 관측이 된 것을 확인하였다. 또한, 2019년 겨울에 주로 관측이 되었다. 반면, 1800 UTC에 MOG 관측 비율이 0.71%로 가장 낮았다.

Hourly number of observations by intensity and percentage of MOG observations (bar graph and line graph, respectively).
정리하면, 한반도 상층에서 비행하는 항공기는 24시간 운영하는 인천국제공항을 제외한 대부분의 공항이 운영되는 시간인 0300~1000 UTC에 주로 운항되며, 낮 시간대가 새벽 및 밤 시간대에 비하여 대류 활동도 활발해지기 때문에 MOG 난류 관측 수가 증가했을 것으로 판단된다(Kim et al., 2009). 따라서 모든 시간의 예측이 중요하지만 특히 낮 시간대 예측이 중요한 것으로 보인다.
마지막으로 고도에 따른 관측자료수와 MOG 난류 관측 비율을 Fig. 6에 나타내었다. 고도는 5,000 ft 단위로 분석을 진행하였다. 즉, 20,000~25,000 ft, 25,000~30,000 ft, 30,000~35,000 ft, 35,000~40,000 ft 40,000 ft 이상으로 나누어 분석을 진행하였다. 총 관측자료수는 30,000~35,000 ft에서 가장 관측자료수가 많았으며(140,232개), 35,000~40,000 ft (131,363개), 25,000~30,000 ft (70,889개), 20,000~25,000 ft (62,092개), 40,000 ft 이상(19,265개) 순서로 많았다. LGT와 MOG 난류 관측자료수도 유사한 경향성으로 나타났으며, 특히 고도 30,000~35,000 ft에서 LGT 난류 관측자료수가 다른 고도들에 비하여 약 2배 이상 많이 관측되었다. 이 고도에서 LGT 난류 관측 비율은 7.83%로 다른 고도(3.07~3.96%)에 비해 LGT 난류를 조우할 가능성이 크다. MOG 난류 관측 비율은 20,000~35,000 ft에서 1.14~1.15%이었으며, 다른 고도에서는 0.98~1.02%로 상대적으로 약간 낮았다. 하지만 변동성이 크지 않아 전 고도에서 MOG 난류를 조우할 가능성이 비슷할 것으로 사료된다. 그러나 관측 빈도수로 보았을 때, 고도 30,000~35,000 ft에서 많이 관측되었으므로, 해당 고도에서 항행을 할 때 항공 난류에 대해 보다 더 많은 주의가 필요하다.
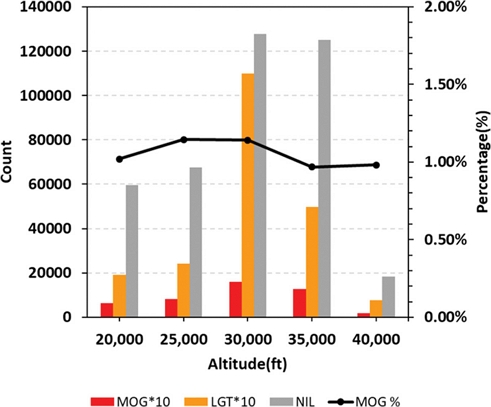
Number of observations by intensity and percentage of MOG observations for altitudes from 20,000 ft to 40,000 ft (bar graph and line graph, respectively).
마지막으로, 선행연구에서는 PIREPs 자료를 주로 사용하여 분석이 되어왔다(Kim and Chun, 2011; Lee and Chun, 2015). 따라서 관측 방식에 따른 난류 특성 차이가 있는지 살펴보기 위해 PIREPs 자료와 in-situ EDR 자료 간의 특성을 비교하였다. PIREPs 자료는 비행 중에 조종사가 조우한 기상현상보고로 비행기 크기와 조종사에 의존되어 난류 강도 측정이 주관적으로 이루어진다. 반면, in-situ EDR 자료는 비행기 기체에 기기를 부착하여 바람을 측정하고 EDR 규모로 환산하여 산출되므로 난류 강도 측정이 객관적으로 이루어진다. 본 연구에서는 Lee and Chun (2015)이 분석한 결과를 활용하여 PIREPs 자료와 in-situ EDR 자료의 한반도 상공의 항공 난류 특성을 비교하였다. Lee and Chun (2015)는 PIREPs 자료를 이용하여 2002.12~2012.11(10년)의 장기간 한반도 상공의 항공 난류 특성을 규명하였다. 전체적으로 관측자료수는 PIREPs 자료에 비하여 In-situ EDR 자료가 약 33배 더 많았다. 계절별 MOG 관측 비율은 in-situ EDR 자료와 PIREPs 자료 둘 다 봄에 높고(각각 4.01%, 4.99%), 다음으로 여름이 높은(각각 3.89%, 4.60%) 유사한 계절적 경향성을 보였다. 이러한 결과는 약간의 차이가 있을 수 있으나 전반적으로 PIREPs 자료와 in-situ EDR 자료의 특성이 유사하다는 것을 의미한다.
한편, 월별로 비교했을 때는 MOG 난류 관측 비율이 in-situ EDR 자료가 6월이 가장 높았고, PIREPs 자료는 3~4월에 가장 높았다. 월별 MOG 난류 관측 비율의 차이가 나타난 큰 이유는 분석한 관측 자료 간의 영역이 달라서 나타난 것으로 보인다. PIREPs 자료는 인천 FIR (Flight Information Region) 영역을 분석하였으나, in-situ EDR 자료는 영역이 더 넓은 한반도 주변 바다와 일본의 남서 영역이 포함되어 있다. Lee and Chun (2015)은 내륙 지역보다 해안 주변에서 CIT가 더 많이 관측될 가능성이 높은 것으로 분석하였다. 그러므로, 본 연구에서 사용한 in-situ EDR 자료는 PIREPs 자료에 비하여 CIT 관측과 같은 대류시스템에 의한 난류가 더 많이 포함되었을 가능성이 높으며, 특히 6월에 MOG 난류 관측 비율이 높았던 것으로 판단된다. 다만, Lee and Chun (2015)이 분석한 PIREPs 한반도 월별 CIT 분포에서 7월에 MOG CIT 관측 비율이 최대였는데, 본 연구의 in-situ EDR은 6월에 가장 높았다. 이는 과거에 비하여 지구온난화가 진행됨에 따라 전반적으로 CIT 발생 시기가 더 앞당겨져 MOG CIT 발생이 빈번해졌을 가능성이 있을 것으로 예상된다. 하지만, 본 연구에서는 in-situ EDR 자료에서 난류의 원천을 구별하여 분석하지 않았으며, 심한 난류가 예측된 경우에는 항공기가 피해가기 때문에 관측의 한계성이 존재한다. 그러므로, 이후 더 자세한 연구가 이루어져야 할 것이다.
3.2 통계적 검증 분석
검증은 예측 시간별로 수행하였으며, 예측 시간은 0000 UTC부터 +2100 UTC까지 3시간 간격으로 이루어져있다. 예측 시간 기준으로 ±2시간 관측자료를 이용하여 가장 가까운 격자점에서의 예측값과 비교하였다(e.g. Kim et al., 2011). 먼저 전체 기간, 연도별, 계절별 및 월별 AUC를 살펴봄으로써 K TG 및 G K TG 모델의 전반적인 예측 성능을 평가하였다. 그 후, AUC와 TSS간 상관분석을 통해 MOG 난류에 대한 모델 임곗값에 따른 정확도를 평가하였다.
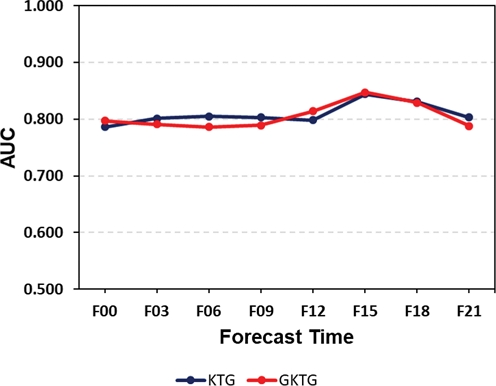
5년 기간 동안 예측 시간별 AUC는 K TG와 G K TG 모두 약 0.78 이상 이였으며(Fig. 8), 예측 시간 평균 AUC는 각각 0.809와 0.805이었다(Fig. 7). 이는 실제 항공산업에 종사하고 있는 실무자들이 높은 신뢰도를 가지고 난류를 판단할 수 있는 예측모델 정확도 수준에 부합하는 예측 성능이다(Fahey, 1993; Sharman et al., 2006; Kim et al., 2009).
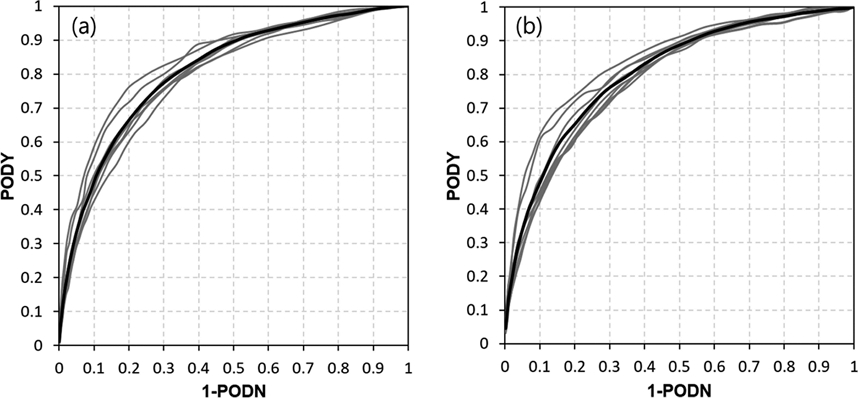
ROC curves for (a) KTG and (b) GKTG. Gray lines represent individual years, black line represents the average across all years.
예측 시간별 모델들의 AUC 결과를 좀 더 자세히 살펴보면(Fig. 8 ), K TG AUC는 0000 UTC에 0.786으로 가장 낮았고 +1500 UTC에 0.844로 가장 높았다. GKTG AUC는 +0600 UTC에 0.786으로 가장 낮았으며, +1500 UTC에 0.847로 가장 높았다(Fig. 8). 하지만 AUC가 약 0.06 사이에서 변동하여 예측 시간에 따른 성능 차이는 크게 없었으며, KTG와 G K TG 모델간의 성능 차이도 거의 없었다.
연도, 계절 및 월 별 AUC 결과는 0000 UTC에서 +2100 UTC까지의 모든 예측 시간에 대하여 평균을 하고 표준편차를 구해 Figs. 9-11에 나타내었다. 연도별로 AUC를 살펴보면(Fig. 9), KTG는 예측 시간 평균 AUC가 2022년(0.791)을 제외하고 2019년(0.796)부터 2023년(0.821)까지 지속적으로 높아졌다. GKTG는 2023년(0.832), 2021년(0.785), 2019년(0.779), 2020년(0.769), 2022년(0.773) 순으로 AUC가 컸다. 예측 시간별 AUC 변동성은 각 연도별로 다르게 나타났으며, 표준편차가 0.023~0.062 사이에서 변동하였다. Kim et al. (2009)는 매 해마다 관측자료의 표본이 달라지고 주요 난류 발생 원인이 달라질 수 있음을 언급하였다. 따라서, 연도별로 난류 발생 원인이 다르게 나타날 수 있기 때문에 연도별로 예측 성능이 달라질 수 있다. 본 연구에서 AUC는 연도별로 변동성이 있었으나, 그 변동성은 크지 않았다.
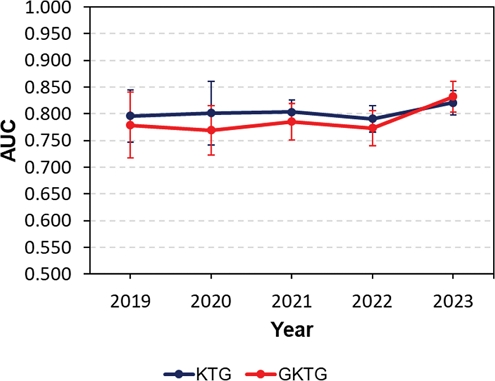
The AUC value by year. The central dot represents the mean AUC value for each forecast time, while the error bars indicate the standard deviation.
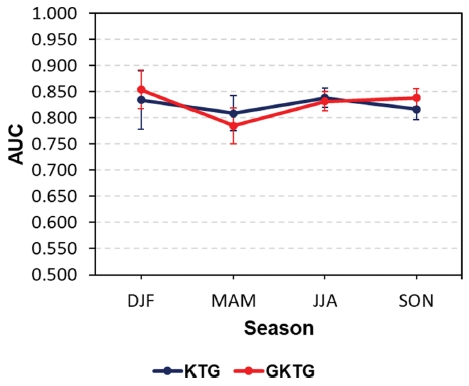
The AUC value by season. The central dot represents the mean AUC value for each forecast time, while the error bars indicate the standard deviation.
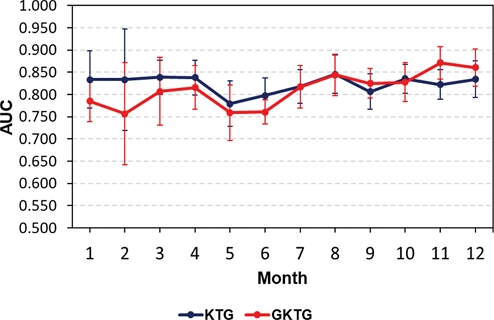
The AUC value by month. The central dot represents the mean AUC value for each forecast time, while the error bars indicate the standard deviation.
다음으로는 계절별 성능에 대한 분석을 진행하였다(Fig. 10). 계절별로 예측 시간 평균 AUC는 K TG의 경우 여름(0.838), 겨울(0.834), 가을(0.817), 봄(0.809) 순으로, GKTG는 겨울(0.854), 가을(0.838), 여름(0.832), 봄(0.785) 순으로 높았다. KTG는 계절별로 큰 차이는 없었으나, GKTG의 경우 비교적 계절별로 성능의 차이가 컸다. 예측 시간별 AUC는 봄, 겨울, 가을에 변동성이 약간 컸다. 낮(+0000~+0600 UTC)과 밤(+1200~+1800 UTC)의 평균 AUC를 살펴보면, 낮보다 밤의 AUC가 0.012~0.030만큼 높았다. 이는 봄, 겨울, 가을에 낮과 밤에 따른 난류 발생 원인의 변동성이 다소 큰 것으로 판단된다. 두 모델 모두 봄에 잘 모의를 못하였는데, 봄에 KTG는 CAT를, GKTG는 CAT와 MWT 뿐만 아니라 다양한 요인으로 인한 항공 난류 발생이 복합적으로 이루어지고 있는 것으로 사료된다. 더 자세하게 살펴보기 위해 월별 분석을 진행하였다.
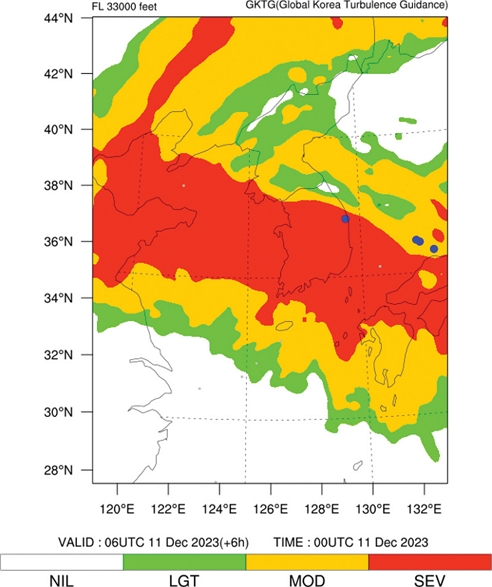
Figure 11에 월별 분석한 결과를 나타내었다. KTG의 예측 시간 평균 AUC는 8월에 0.846으로 가장 높았으며, 5월에 0.780으로 가장 낮았다. GKTG는 11월에 0.871로 가장 높았으며, 2월에 0.757로 가장 낮았다. 전반적으로 KTG의 AUC가 더 높았으며, 7~8월을 기점으로 G K TG가 K TG보다 더 높아지는 것을 확인하였다. 월별 AUC의 변동성은 KTG보다 GKTG가 더 컸다. 예측 시간별 AUC는 두 모델 모두 2월에 표준편차가 0.114~0.115로 변동성이 가장 컸다. 한편, KTG는 10~11월이 가장 변동성이 작았고(0.033), GKTG는 6월에 가장 변동성이 작았다(0.027). KTG는 CAT과 관련된 진단지수들만이 고려되었으며, 전지구 영역 난류 예측을 목적으로 개발된 G K TG에 비하여 동아시아 영역에서 발생하는 난류를 잘 예측하는 난류지수들을 위주로 결합하였기 때문에 G K TG보다 K TG가 한반도 영역을 예측하는데 조금 더 적합했던 것으로 보인다(Kim and Chun, 2012; Lee and Chun, 2018). 또한 GKTG는 산출 과정 중 EDR로 변환하는 과정을 거치면서 불확성이 생길 가능성이 있다(Sharman et al., 2006; Lee and Chun, 2018). 이에 겨울-봄(1~6월)에 K TG의 AUC가 더 높았던 이유는 봄에 제트기류 등이 원인이 되는 CAT 발생이 활발하여 더 잘 예측이 되었던 것으로 판단된다. 한편, 가을(9~12월)에 GKTG의 AUC가 더 높게 나타난 것은 이 시기에 비교적 MWT의 발생이 더 활발했을 것으로 예상되며 이를 G K TG가 잘 예측했던 것으로 판단된다. 결론적으로 K TG와 G K TG에서 사용한 진단지수들과 산출과정이 다르기 때문에 검증 결과에 차이가 다소 나타난 것으로 보인다(Fig. 12).
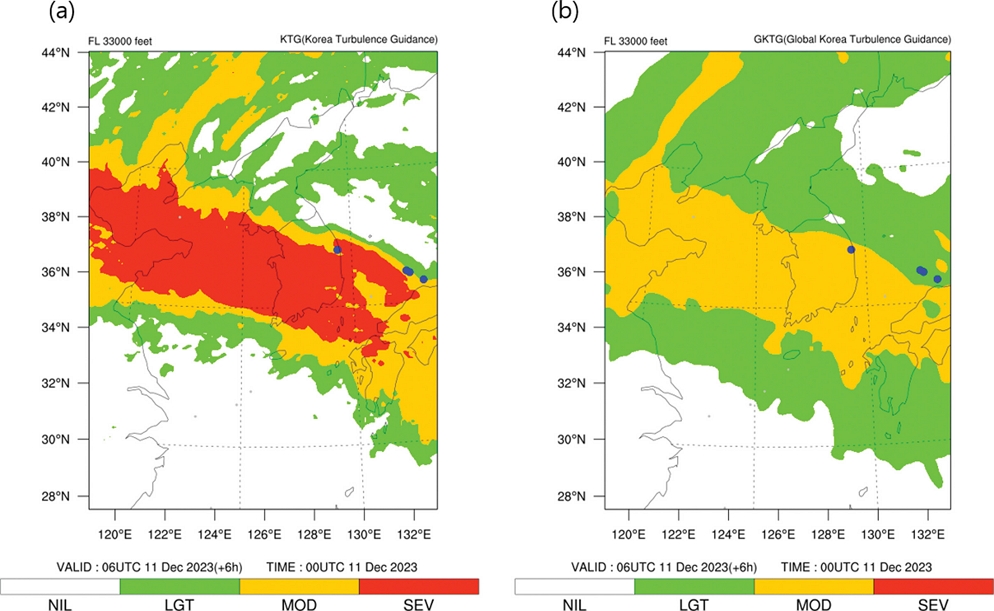
Example of upper-level (a) KTG and (b) GKTG at z = 33,000 ft valid at 0600 UTC 11 Dec 2023 on the Korean peninsula. MOG intensity turbulence in-situ EDRs observed within ±2 hrs of 0600 UTC 11 Dec 2023 and ±500 ft of 33,000 ft are depicted as blue dots.
하지만, 두 모델 모두 여름에 특히 5~6월에 대체적으로 AUC가 낮게 나타났다. 이러한 결과는 CAT 난류지수들을 이용한 K TG와 MWT 난류지수들까지 포함된 G K TG에서 고려되지 못한 원천에서 발생된 난류가 함께 작용되었던 것으로 판단된다. 즉, 5~6월에 CIT 및 NCT와 같은 대류시스템에 기원하는 난류가 복합적으로 작용하여, 두 모델 모두 난류 예측이 잘 이루어지지 못했던 것으로 보여진다.
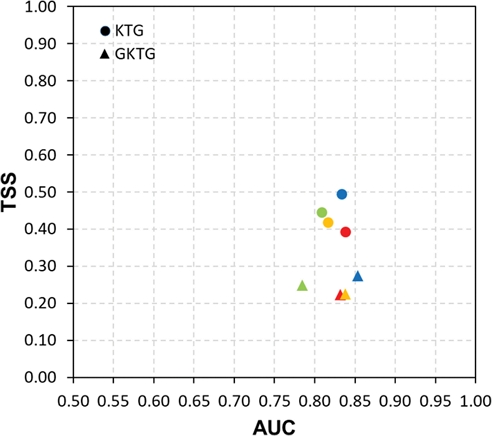
Figure 13은 전체 및 연도별 AUC와 TSS 간 상관관계를 나타내었다. 보다 연한색의 마커는 각 연도별 성능을 나타내었으며, 진한색의 마커는 전체 기간 동안의 성능을 나타내었다. 오차막대는 세로와 가로 각각 TSS와 AUC의 예측 시간별 표준편차를 보여준다. 그래프에서 오른쪽 위로 갈수록 성능이 좋다는 것을 의미한다.
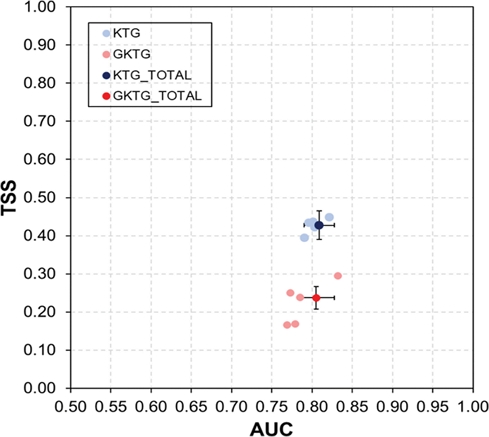
Scatter plot of AUC versus TSS by year and for the total period. Light colors represent individual years, dark colors represent the average over the total period, and error bars show the standard deviation.
위에서 언급했듯이 K TG와 GKTG 두 모델의 AUC는 유사하게 나타났으나, TSS는 K TG는 대체적으로 약 0.4 이상, GKTG는 약 0.3 이하에 분포되어있다. 전체 기간 동안 GK TG는 K TG에 비하여 TSS가 0.19 낮았다. 정리하면, 결과적으로 두개의 항공 난류 예측모델 중 G K TG보다 K TG의 성능이 더 좋았다. AUC는 유사하나 TSS는 낮게 나타난 G K TG의 결과는 예측모델의 전반적인 성능은 좋았으나, 현재 임곗값에서 MOG 난류를 예측하는 정확도(PODY)가 떨어져서 이러한 결과가 나온 것으로 보여진다.
더 나아가, 계절별 AUC와 TSS 간 상관관계를 분석한 결과를 Fig. 14에 나타내었다. 두 모델 모두 겨울에 성능이 가장 좋았다. KTG의 경우 봄과 가을에 TSS가 약 0.4 이상으로 높았으나 AUC가 0.809~0.817로 비교적 낮았고, 여름에는 AUC가 0.838으로 높았으나 TSS가 0.39로 낮았다. GKTG는 TSS가 봄에 0.25로, 0.22로 나타난 여름과 가을에 비해 높았고 AUC는 여름과 가을에 0.838~0.832로 0.785인 봄보다 더 높았다. 한편, 두 모델 모두 여름에 TSS가 낮게 나타났다. 즉, 사계절 모두 같은 임곗값을 사용했음에도 불구하고 여름에 MOG 난류 예측 정확도가 다소 떨어져서 이러한 결과가 나온 것으로 보인다. 여름에는 장마 전선 및 태풍 등과 같은 중규모 대류계의 발달과 대류성 구름의 발달로 인한 CIT가 활발해지기 때문에(Kim and Chun, 2011; Lee and Chun, 2015), 본 연구에서 사용한 CAT을 주로 예측하는 모델에서는 비교적 잘 모의가 안되었던 것으로 판단된다.
3.3 모델 개선 및 적용
위에서 AUC와 TSS의 비교분석을 통한 항공 난류 예측모델의 성능평가를 진행하였다. AUC는 모델 임곗값에 독립적이지만, TSS는 모델 임곗값에 의존적이다. 그러므로 AUC 기반 높은 예측성의 예측모델임에도 불구하고 TSS 값이 낮을 경우, 이는 현재 선택된 모델 임곗값이 최적이 아닐 수 있음을 시사한다. 따라서 in-situ EDR 난류 관측자료와 항공 난류 예측모델 자료를 비교하여 한반도 상층에서의 MOG 난류 예측을 위한 최적의 모델 임곗값을 산출하여 항공 난류 예측모델을 개선하였다.
항공 난류 예측모델의 개선은 가장 많은 관측 개수가 분포되어있는 +0600 UTC를 기준으로 진행하였으며, 모델 임곗값 변화에 따른 K TG와 G K TG의 TSS를 Fig. 15에 나타내었다. 검정색 실선은 TSS가 가장 높았던 지점의 임곗값에 대한 선이고, 검정색 점선은 현재의 임곗값일때의 선이다. KTG와 GKTG 각각 현재의 임곗값(0.22, 0.475)일 때 TSS는 0.42, 0.20이다. 한편, GKTG와 K TG를 최적 임곗값(0.385, 0.17)으로 변경했을 때 TSS는 각각 0.46, 0.42로 나타났다. KTG는 개선 전과 후의 TSS 차이가 0.02로 많이 개선이 되지는 않았지만, GKTG는 TSS가 0.22 증가하여 상당히 개선이 많이 되었다. 이러한 결과를 통하여 임곗값을 조정함으로써 모델의 예측성능을 향상시킬 수 있음을 확인할 수 있었다. 위와 같은 결과를 기반으로 현재 기상청에서는 GKTG에 대하여 최적의 MOG 난류 임곗값으로 개선하여 적용하였으며(Fig. 16), 2024년 5월부터 개선된 항공 난류 예측모델자료를 제공하고 있다.
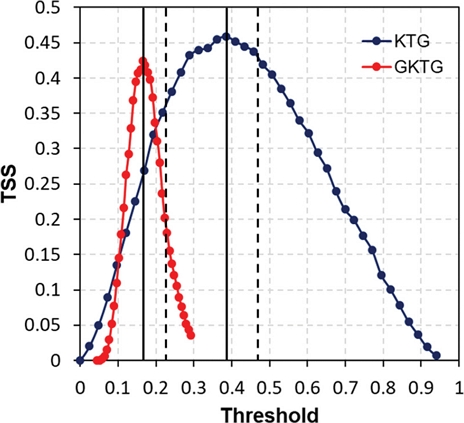
TSS values for KTG and GKTG at various thresholds. The dashed line indicates the existing threshold, while the solid line represents the improved threshold.
4. 요약 및 결론
본 연구에서는 5년간(2019~2023년) 고도 20,000 ft 이상의 한반도 영역(27.5~44oN, 119~135oE)에서 관측된 in-situ EDR 자료를 사용하여 한반도 상층 난류 발생에 대한 시∙공간적 통계분석을 진행하였다. 그리고 in-situ EDR 관측자료와 기상청 현업 항공 난류 예측모델(KTG, GKTG) 예측자료를 비교하여 AUC를 살펴봄으로써 모델의 전반적인 예측 성능을 평가하고, AUC와 TSS간 상관분석을 통해 MOG 임곗값에서의 정확도를 평가하였다. 더 나아가 예측모델 개선을 수행하였다.
전체적으로 한반도 영역에서 관측된 자료들은 항공로를 따라 관측이 되었으며, 난류 강도가 강해질수록 급격하게 관측자료수가 감소하였다. 연도별 관측자료수는 전반적으로 시간이 지남에 따라 증가하는 추세를 보였으며, 특히, 2023년에 NIL 난류 관측자료수가 급격하게 증가하였다. MOG 강도의 난류 관측 자료수는 매년 증가하는 경향을 보였으나, MOG 난류 관측 비율은 2019년부터 2023년까지 지속적으로 감소했다. 이는 항공기 운항 수가 증가하면서 관측자료수도 증가하였으며, 그에 따른 MOG 난류에 대한 예측 및 회피 능력 또한 향상되고 있음을 의미한다.
계절별 총 관측자료수는 가을, 여름, 봄, 겨울 순으로 많았으며, 월별로는 12월에 가장 관측자료수가 많았다. MOG 난류 관측 비율은 봄, 여름, 가을, 겨울 순으로 높았다. 월별로는 5~6월에 MOG 난류 관측 비율이 높았으며, 10~11월에 가장 낮았다. 계절별 및 월별로 MOG의 난류 관측 비율이 다른 이유는 난류의 발생 원인이 달랐기 때문인 것으로 판단된다. 겨울에는 발달된 상층 전선 및 강한 제트기류 지역에서 발생하는 시어불안정과 관성불안정이 기원이 되고, 여름철에는 중규모 대류계의 발달로 인한 강한 대류시스템이 항공 난류 발생의 주요 원인이며, 봄에는 대류운 및 대류시스템의 영향과 강한 제트기류 모두가 항공 난류가 발생하는 주요 매커니즘으로 작용했을 것으로 판단된다(Dutton and Panofsky, 1970; Ellrod and Knapp, 1992; kim et al., 2009; Kim and Chun, 2011; Lee and Chun, 2015; Miyamoto et al., 2023). 하지만, 본 연구에서는 관측자료를 난류의 발생원에 따라 분류하여 분석하지 않았기 때문에 계절적 변화에 대해 더 상세하게 규명하기 위해서는 항공 난류 기원에 따른 분석이 추가적으로 필요할 것으로 보인다.
마지막으로, 한반도 상층에서 관측되는 MOG 난류 관측 비율은 낮에 높았으며, 고도 30,000~35,000 ft에서 가장 빈번하게 관측되었다. 그러므로 MOG 난류가 특히 많이 관측되는 계절, 시간 및 고도에서 비행하는 항공기는 강한 난류의 조우 가능성이 다른 때보다 높아 항행시 더 많은 주의가 필요하다.
5년간 KTG와 GKTG의 검증결과는 예측 시간 평균 AUC가 각각 0.809와 0.805으로, 이는 실제 항공산업에 종사하는 실무자들이 유의미하게 현업 예보에 활용할 수 있는 예측모델 정확도 수준에 부합한다(AUC = 0.8; Fahey, 1993; Sharman et al., 2006; Kim et al., 2009). 연도별 예측 시간 평균 AUC는 K TG와 GKTG 모두 대체적으로 시간이 지날수록 정확도가 높아졌으며(0.773~0.832), 계절별로는 K TG가 여름(0.838), 겨울(0.834), 가을(0.817), 봄(0.809) 순으로, GKTG는 겨울(0.854), 가을(0.838), 여름(0.832), 봄(0.785) 순으로 예측 시간 평균 AUC가 높았다. 더 나아가 월별 KTG와 G K TG 예측 시간 평균 AUC는 각각 8월(0.846), 11월(0.871)에 가장 높았으며, 5월(0.780), 2월(0.757)에 가장 낮았다. 또한, 7~8월을 기점으로 G K TG가 KTG보다 더 높아지는 것을 확인하였다. 이는 KTG는 CAT을 중점으로 예측되며, GKTG는 CAT와 MWT가 함께 고려되어 예측이 되기 때문에 계절별로 예측 성능의 차이가 나타난 것으로 보인다. 그리고 두 모델 모두 특히 5~6월에 AUC가 낮았던 것은 KTG와 GKTG에서 고려되지 못한 원천의 난류, 즉 대류시스템 기원의 난류가 복합적으로 작용하였기 때문으로 판단된다.
전체 및 연도별 AUC와 TSS 간 상관관계를 살펴보면, KTG와 G K TG 두 모델의 AUC는 유사하게 나타났으나, TSS는 K TG(약 0.4 이상)가 G KTG(약 0.3 이하)보다 높았다. 이러한 결과는 항공 난류 예측모델에서 G K TG보다 K TG의 성능이 더 좋았다는 것을 의미한다. TSS 결과를 기준으로 두 모델 모두 겨울에 성능이 가장 좋았으며, 여름에는 정확도가 비교적 낮았다. 여름에는 장마 전선 및 태풍 등과 같은 중규모 대류계의 발달과 대류성 구름의 발달로 인한 CIT가 활발해져, 비교적 잘 모의가 안되었던 것으로 보인다.
검증 결과를 통하여 GKTG가 AUC가 높은 예측 정확도를 가지고 있음에도 불구하고 TSS 값이 낮은 것을 확인하였고, 이는 현재 선택된 임곗값이 최적이 아닐 수 있음을 나타낸다. 이에, MOG 난류 강도에 대한 최적의 임곗값을 도출하기 위한 임곗값 변화에 따른 예측 성능 민감도 실험을 수행하였다. 그 결과 GKTG의 임곗값을 0.22에서 0.17로 변경하였을 때, TSS 값이 0.20에서 0.42로 상당히 개선되었음을 확인하였다. 현재 기상청에서 2024년 5월부터 GKTG에 대해 최적의 MOG 강도 난류 임곗값(0.17)으로 개선 적용하여 예측자료를 산출하고 있다. 하지만, 이러한 개선은 MOG 난류를 중점으로 개선하였기에 약한 강도의 난류가 예측될 때 과대 모의될 가능성이 있다. 따라서 더욱 정밀하게 개선하기 위해서는 개별 난류 진단 지수에 대해 더 자세히 살펴보거나 위의 문제점들을 반영한 임곗값 재선정 및 모델의 개선이 필요하다.
이러한 결과를 토대로 현재 기상청에서 사용 중인 모델들은 주로 CAT와 MWT 예측에 초점이 맞추어져 있다. 향후 연구에서는 CIT 및 NCT와 같은 대류시스템 기원의 난류 예측 능력을 향상시키는 것이 필요할 것으로 보인다. 이러한 개선은 한반도 상공의 항공안전을 더욱 강화하는 데 기여될 것으로 기대된다.
Acknowledgments
본 논문의 개선을 위해 좋은 의견을 제시해 주신 두 분의 심사위원께 감사를 드립니다. 이 연구는 기상청 국립기상과학원 수요자 맞춤형 기상정보 산출기술 개발사업(KMA2018-00622)의 지원으로 수행되었습니다.
References
-
Allouche, O., A. Tsoar, and R. Kadmon, 2006: Assessing the accuracy of species distribution models: prevalence, kappa and the true skill statistic (TSS). J. Appl. Ecology, 43, 1223-1232.
[https://doi.org/10.1111/j.1365-2664.2006.01214.x]

-
Belo-Pereira, M., 2015: Comparison of in-flight aircraft icing algorithms based on ECMWF forecasts. Meteor. Appl., 22, 705-715.
[https://doi.org/10.1002/met.1505]

-
Chambers, E., 1955: Clear air turbulence and civil jet operations. J. Roy. Aeronautical Soc., 59, 613-628.
[https://doi.org/10.1017/S036839310011692X]

-
Cho, J. Y. N., and E. Lindborg, 2001: Horizontal velocity structure functions in the upper troposphere and lower stratosphere: 1. Observations. J. Geophys. Res. Atmos., 106, 10223-10232.
[https://doi.org/10.1029/2000JD900814]

-
Cornman, L. B., C. S. Morse, and G. Cunning, 1995: Real-time estimation of atmospheric turbulence severity from in-situ aircraft measurements. J. Aircraft, 32, 171-177.
[https://doi.org/10.2514/3.46697]

-
Dutton, J. A., and H. A. Panofsky, 1970: Clear air turbulence: A mystery May be unfolding: High altitude turbulence poses serious problems for aviation and atmospheric science. Science, 167, 937-944.
[https://doi.org/10.1126/science.167.3920.937]

-
Ellrod, G. P., and D. I. Knapp, 1992: An objective clear-air turbulence forecasting technique: Verification and operational use. Wea. Forecasting, 7, 150-165.
[https://doi.org/10.1175/1520-0434(1992)007<0150:AOCATF>2.0.CO;2]

- Fahey, T. H., 1993: Northwest Airlines atmospheric hazards advisory and avoidance system. International Conference on Aviation Weather Systems, 5th, Vienna, 409-413.
-
Fielding, A. H., and J. F. Bell, 1997: A review of methods for the assessment of prediction errors in conservation presence/absence models. Environmental conservation, 24, 38-49 [Available online at http://www.jstor.org/stable/44519240, ].
[https://doi.org/10.1017/S0376892997000088]

-
Gill, P. G., and P. Buchanan, 2014: An ensemble based turbulence forecasting system. Meteorol. Appl., 21, 12-19.
[https://doi.org/10.1002/met.1373]

-
Jaeger, E. B., and M. Sprenger, 2007: A Northern Hemispheric climatology of indices for clear air turbulence in the tropopause region derived from ERA40 reanalysis data. J. Geophys. Res. Atmos., 112, D20106.
[https://doi.org/10.1029/2006JD008189]

- Kim, J.-H., H.-Y. Chun, W. Jang, and R. D. Sharman, 2009: A study of forecast system for clear-air turbulence in Korea, Part II: Graphical Turbulence Guidance (GTG) system. Atmosphere, 19, 269-287.
-
Kim, J.-H., and H.-Y. Chun, 2011: Statistics and possible sources of aviation turbulence over South Korea. J. Appl. Meteor. Climatol., 50, 311-324.
[https://doi.org/10.1175/2010JAMC2492.1]

-
Kim, J.-H., H.-Y. Chun, R. D. Sharman, and T. L. Keller, 2011: Evaluations of upper-level turbulence diagnostics performance using the Graphical Turbulence Guidance (GTG) system and Pilot Reports (PIREPs) over East Asia. J. Appl. Meteor. Climatol., 50, 1936-1951.
[https://doi.org/10.1175/JAMC-D-10-05017.1]

-
Kim, J.-H., and H.-Y. Chun, 2012: A numerical simulation of convectively induced turbulence above deep convection. J. Appl. Meteor. Climatol., 51, 1180-1200.
[https://doi.org/10.1175/JAMC-D-11-0140.1]

-
Kim, J.-H., R. Sharman, M. Strahan, J. W. Scheck, C. Bartholomew, J. C. Cheung, P. Buchanan, and N. Gait, 2018: Improvements in nonconvective aviation turbulence prediction for the World Area Forecast System. Bull. Amer. Meteor. Soc., 99, 2295-2311.
[https://doi.org/10.1175/BAMS-D-17-0117.1]

-
Kim, S.-H., H.-Y. Chun, D.-B. Lee, J.-H. Kim, and R. D. Sharman, 2021: Improving numerical weather prediction-based near-cloud aviation turbulence forecasts by diagnosing convective gravity wave breaking. Wea. Forecasting, 36, 1735-1757.
[https://doi.org/10.1175/WAF-D-20-0213.1]

-
Koch, P., H. Wernli, and H. C. Davies, 2006: An event-based jet-stream climatology and typology. Int. J. Climatol., 26, 283-301.
[https://doi.org/10.1002/joc.1255]

-
Lane, T. P., R. D. Sharman, S. B. Trier, R. G. Fovell, and J. K. Williams, 2012: Recent advances in the understanding of near-cloud turbulence. Bull. Amer. Meteor. Soc., 93, 499-515.
[https://doi.org/10.1175/BAMS-D-11-00062.1]

-
Lee, D.-B., and H.-Y. Chun, 2015: A statistical analysis of aviation turbulence observed in pilot report (PIREP) over East Asia including South Korea. Atmosphere, 25, 129-140.
[https://doi.org/10.14191/Atmos.2015.25.1.129]

-
Lee, D.-B., and H.-Y. Chun, 2018: Development of the Global-Korean aviation turbulence guidance (Global-KTG) system using the global data assimilation and prediction system (GDAPS) of the Korea meteorological administration (KMA). Atmosphere, 28, 223-232.
[https://doi.org/10.14191/Atmos.2018.28.2.223]

-
Lee, D.-B., H.-Y. Chun, S.-H. Kim, R. D. Sharman, and J.-H. Kim, 2022: Development and evaluation of global Korean aviation turbulence forecast systems based on an operational numerical weather prediction model and in situ flight turbulence observation data. Wea. Forecasting, 37, 371-392.
[https://doi.org/10.1175/WAF-D-21-0095.1]

-
Lee, J. H., J.-H. Kim, R. D. Sharman, J. Kim, and S.-W. Son, 2023: Climatology of clear-air turbulence in upper troposphere and lower stratosphere in the Northern Hemisphere using ERA5 reanalysis data. J. Geophys. Res. Atmos., 128, e2022JD037679.
[https://doi.org/10.1029/2022JD037679]

-
Lee, S. H., P. D. Williams, and T. H. A. Frame, 2019: Increased shear in the North Atlantic upper-level jet stream over the past four decades. Nature, 572, 639-642.
[https://doi.org/10.1038/s41586-019-1465-z]

-
Lester, P., 1994: Understanding turbulence through the analysis of DFDR information. In 32nd Aerospace Sciences Meeting and Exhibit, 269 pp.
[https://doi.org/10.2514/6.1994-269]

- Mason, S. F., 1982: Molecular optical activity and the chiral discriminations. Cambridge University Press, 273 pp.
-
Miyamoto, Y., A. Matsumoto, and S. Ito, 2023: Statistical analysis of aviation turbulence in the middle-upper troposphere over Japan. J. Appl. Meteor. Climatol., 62, 575-588.
[https://doi.org/10.1175/JAMC-D-21-0191.1]

-
Sharman, R. D., C. Tebaldi, G. Wiener, and J. Wolff, 2006: An integrated approach to mid-and upper-level turbulence forecasting. Wea. Forecasting, 21, 268-287.
[https://doi.org/10.1175/WAF924.1]

-
Sharman, R. D., S. B. Trier, T. P. Lane, and J. D. Doyle, 2012: Sources and dynamics of turbulence in the upper troposphere and lower stratosphere: A review. Geophys. Res. Lett., 39, L12803.
[https://doi.org/10.1029/2012GL051996]

-
Sharman, R. D., L. B. Cornman, G. Meymaris, J. Pearson, and T. Farrar, 2014: Description and derived climatologies of automated in situ eddy-dissipation-rate reports of atmospheric turbulence. J. Appl. Meteor. Climatol., 53, 1416-1432.
[https://doi.org/10.1175/JAMC-D-13-0329.1]

-
Sharman, R. D., and T. Lane, 2016: Aviation turbulence. Springer International Publishing, Switzerland, 523 pp.
[https://doi.org/10.1007/978-3-319-23630-8]

-
Sharman, R. D., and J. M. Pearson, 2017: Prediction of energy dissipation rates for aviation turbulence. Part I: Forecasting non convective turbulence. J. Appl. Meteor. Climatol., 56, 317-337.
[https://doi.org/10.1175/JAMC-D-16-0205.1]

-
Storer, L. N., P. D. Williams, and M. M. Joshi, 2017: Global response of clear-air turbulence to climate change. Geophys. Res. Lett., 44, 9976-9984.
[https://doi.org/10.1002/2017GL074618]

-
Storer, L. N., P. D. Williams, and P. G. Gill, 2019: Aviation turbulence: dynamics, forecasting, and response to climate change. Pure Appl. Geophy., 176, 2081-2095.
[https://doi.org/10.1007/s00024-018-1822-0]

-
Tebaldi, C., D. Nychka, B. G. Brown, and R. D. Sharman, 2002: Flexible discriminant techniques for forecasting clear-air turbulence. J. Int. Environmentrics Soc., 13, 859-878.
[https://doi.org/10.1002/env.562]

-
Tenenbaum, J., and Coauthors, 2022: Aircraft observations and reanalysis depictions of trends in the North Atlantic winter jet stream wind speeds and turbulence. Quart. J. Roy. Meteor. Soc., 148, 2927-2941.
[https://doi.org/10.1002/qj.4342]

-
Tung, K. K., and W. W. Orlando, 2003: The k-3 and k-5/3 energy spectrum of atmospheric turbulence: Quasigeostrophic two-level model simulation. J. Atmos. Sci., 60, 824-835.
[https://doi.org/10.1175/1520-0469(2003)060<0824:TKAKES>2.0.CO;2]

-
Williams, P. D., 2017: Increased light, moderate, and severe clear-air turbulence in response to climate change. Adv. Atmos. Sci., 34, 576-586.
[https://doi.org/10.1007/s00376-017-6268-2]