ERA5 2 m 대기 온도 데이터를 활용한 확률적 모델링 및 분석

1. 서 론

기후 데이터는 시간에 따라 변화하는 시계열(time series) 데이터로 장기적인 추세, 평균적인 기후 상태, 계절적인 변동성을 포함하는 복잡한 특징을 지닌다(Mudelsee, 2019). 이러한 특징의 분석은 기후 변화를 이해하고 예측하는 데 중요한 역할을 한다. 지구 시스템의 특성상 계절 변화는 지구의 자전, 공전과 같은 천문학적 요소로 인해 발생하며, 이는 기온, 강수량, 바람 패턴 등 다양한 기후 요소에 영향을 미친다(Milankovitch, 1941). 예를 들어, 지구의 자전축이 기울어져 있어 태양에 대한 각도가 계절마다 변하며, 이는 계절적 변동성(seasonal variability)을 초래한다(Berger, 1978).

실제 기후 데이터를 보면, 계절적 변동성뿐만 아니라 일정한 주기를 가지고 반복되는 다양한 기상 현상들을 볼 수 있다. 예를 들어, 매든-줄리안 진동(MJO, 약 30~60일 주기), 엘니뇨-남방진동(ENSO, 약 2~7년 주기), 태평양 10년 주기 진동(PDO, 약 20~30년 주기) 등 서로 다른 주기를 가지는 다양한 기상 현상들이 존재하기 때문에, 기후 데이터는 주파수 영역에서 주기가 다른 여러가지 주파수 성분들이 반복되는 주기성을 가진다. 이러한 장주기성이 계절변동과 연계한다.

순환 정적(cyclostationary) 시계열은 시간 도메인에서 주기성을 가지는 시계열로, 자기상관 함수와 같은 통계량과 주파수 영역의 특정 주파수 성분들이 시간에 따라 주기적으로 변화하는 것을 특징으로 한다(Gardner, 1991, 1994). 이러한 특징을 활용하여 신호가 가진 주기성과 구조적 정보를 분석할 수 있다. 하지만 기후 데이터와 같이 서로 다른 주기를 가진 여러 현상이 반영된 데이터에서는 주파수 영역에서 여러 주기가 1년의 정확한 주기를 가지는 계절 변동과 중첩되어 각 현상에 대한 주기를 분석하기 어려워지는 주파수 중복성(frequency redundancy)이 발생할 수 있다. 그렇기 때문에 순환 정적 시계열을 바탕으로 기후 데이터의 변동성을 해석할 때 주의가 필요하다.

Kim et al. (1996)은 순환 정적 시계열을 기후 연구에 도입하여, 기후 데이터를 순환 정적 시계열로 분류하였다. 이를 바탕으로 Bloch의 정리에 기반한 순환 정적 직교 함수(cyclostationary empirical orthogonal functions, CSEOFs) 알고리즘을 개발하여 다양한 주파수 별 모드(mode)의 확률 모델을 구축하였다. CSEOFs 관련 고유값(eigenvalues)은 관측 데이터와 유사한 결과를 보였으며, 각 주기 별 확률 모델의 결과도 원래 데이터를 합리적으로 재현하였다. 그러나 이 방법은 계산 과정이 복잡하고, 각 주파수 별로 많은 모드가 발생해 분석에 어려움을 겪을 수 있으며, 주파수 중 복성 문제 또한 발생할 수 있다.

이러한 분석의 어려움을 극복하고자, Moon and Wettlaufer (2017)은 전 지구 월별 평균 시계열 데이터를 활용하여 기존의 복잡한 시계열 분석을 단순화한 새로운 기후 데이터 분석 방법을 제시하였다. 이 방법은 단순화된 기후모델을 사용하여 계절 별로 전 지구 모든 지역에 대한 안정도를 산출하고 이를 통해 지역, 계절 별 기후 민감도를 분석할 수 있는 점에서 큰 의의를 가진다. 계절별 변동성뿐만 아니라, 해양과 지구온난화 같은 장기 강제력에 의해 서서히 변하는 장기적 추세 또한 도출할 수 있다. 이러한 방법론을 통해, 순환 정적 시계열 분석에서 주파수 중복성과 같은 단점을 극복하고 보다 단순화된 과정으로 기후 데이터를 효과적으로 분석할 수 있다.

본 연구에서는 Moon and Wettlaufer (2017)의 방법을 활용하여 기후 데이터를 분석하고, 전 지구 모든 지역에 대한 안정도, 노이즈(noise), 장기적 영향을 구하는 방법을 소개한다. 이를 바탕으로 극 지역에서 피드백 작용에 의해 발생하는 불안정과 Arctic amplification (AA)에 의해 늦여름에 발생하는 불안정을 분석한다. 또한, 본 연구의 방법론을 통해 구한 수치들을 기반으로 통계 모델을 구축하여 남극의 불안정 지역에 대한 통계적 모델링을 진행한다. 본 논문의 2장에서는 수치들을 구하기 위한 자료와 방법론을 자세히 설명하고, 3장에서는 계산된 수치에 대한 해석을 제시한다. 마지막으로 4장에서는 본 연구의 전체적인 요약과 주요 결과를 논의한다.

2. 자료 및 방법

2.2 모델의 구축

Surface energy flux balance model을 이용하여 온도 T에 대해 구성한 단순 기후 모델은 다음과 같이 표현된다:

$\[ {\rho }_{air}{c}_p{H}_{air}\frac{dT}{dt}=Q^{\mathrm{*}}\left(t, T\right)+N^{\mathrm{*}}\left(t\right)\xi \left(t\right)+F^{\mathrm{*}}\left(\tau \right) \]$

(1)

해당 모델을 구성하고 있는 항들을 살펴보면, Q^*(t, T)는 태양복사에너지(shortwave), 지구복사에너지(longwave)와 같이 계절에 따라 변하는 계절적 강제력(seasonal forcing)을 나타내는 항이다. 또한 N^*(t)ξ(t)는 날씨와 관련된 노이즈의 강제력을 뜻하며, F^*(τ)는 해양과 지구온난화 같은 장기적인 강제력과 관련이 있다.

Q^*(t, T)는 계절 변화에 의한 강제력을 나타내는 항이기 때문에, 가 되어 1년의 주기를 가지는 주기함수로 표현된다. ξ(t)는 가우시안 백색 노이즈(gaussian white noise)를 의미하며, F^*(τ)에서 τ는 τ = εt, ε << 1로, 계절적인 시간 척도를 나타내는 t와는 다르게 장기적인 시간 척도를 뜻한다. 위 모델을 ρ_airc_pH_air로 나누어 정리한 단순화된 모델 식은 다음과 같다:

$\[ \frac{dT}{dt}=Q\left(t, T\right)+N\left(t\right)\xi \left(t\right)+F\left(\tau \right) \]$

(2)

우리는 변동성을 살펴보기 위해 평균장을 제거한 후 섭동장을 분석할 것이므로 온도를 평균장과 섭동장으로 구분하여 전개한다. 날씨와 관련된 노이즈는 계절적 강제력보다 영향이 작으므로 |Q(t, <T>)| >> N(t)을 사용하여 모델의 평균장을 다음과 같이 정의한다.

$\[ \frac{d〈T〉}{dt}=Q\left(t, 〈T〉\right)+〈F〉 \]$

(3)

평균장에 사용된 <ㆍ>는 모든 년도에 대한 월 별 평균을 의미한다. 식(2)에서 레이놀즈 분해(Reynolds decomposition)를 사용하여 T=<T>+x, F(τ)=<F>+f(τ)으로 T와 F(τ)를 평균장과 섭동장으로 구분한다:

$\[ \begin{array}{c}\frac{d}{dt}\left(〈T〉+x\right)=Q\left(t, 〈T〉+x\right)+N\left(t\right)\xi \left(t\right)+〈F〉+f\left(\tau \right)\hfill \\ \simeq Q\left(t, 〈T〉\right)+{\left.\frac{\partial Q}{\partial T}\right|}_{T=〈T〉}x+N\left(t\right)\xi \left(t\right)+〈F〉+f\left(\tau \right)\hfill \end{array} \]$

(4)

$\[ \frac{dx}{dt}=a\left(t\right)x+N\left(t\right)\xi \left(t\right)+f\left(\tau \right) \]$

(5)

식(4)에서 앞서 정의했던 모델의 평균장 식(3)을 빼 준 뒤, $$ {\left.a\left(t\right)=\frac{\partial Q}{\partial T}\right|}_{T=〈T〉}$$로 정의하면 섭동장으로 이루어진 최종 모델 식(5)를 얻을 수 있다. 식(5)에서 a(t)는 계절적 안정도(seasonal stability)를 의미하며, 이에 대한 자세한 설명은 2.2.1장에서 다룰 것이다. 계절적 안정도 a(t)가 양의 값을 가지면 해당 지역이 불안정하며, 음의 값을 가지면 해당 지역이 안정한 상태임을 나타낸다. 이제 식(5)를 이용하여 계절적 안정도와 노이즈 크기(noise amplitude), 장기 강제력(long-term forcing)과 장기 강제력의 영향(long-term forcing effect)를 구하는 과정들을 다룰 것이다.

2.2.1 a(t)의 물리적 의미

$$ {\left.a\left(t\right)=\frac{\partial Q}{\partial T}\right|}_{T=〈T〉}$$로 정의한 a(t)가 계절적 안정도를 나타내는 것에 대한 자세한 설명을 이번장에서 다룰 것이다. 식(2)에서 계절적 강제력이 a(t)와 직접적으로 연관된 항이기 때문에 계절적 강제력을 나타내는Q(t, T) 항만 가져와서 미분 방정식을 풀어줄 것이다.

$\[ \frac{dT}{dt}=Q\left(t, T\right) \]$

(6)

2.2장에서 사용한 방식 그대로 레이놀즈 분해인 T=<T>+x을 이용하여 평균장과 섭동장을 분리한다.

$\[ \frac{d}{dt}\left(〈T〉+x\right)=Q\left(t, 〈T〉+x\right)\simeq Q\left(t, 〈T〉\right)+{\left.\frac{\partial Q}{\partial T}\right|}_{T=〈T〉}x \]$

(7)

여기서 평균장의 식은 $$ \frac{d〈T〉}{dt}=Q\left(t, 〈T〉\right)$$ 이므로 평균장을 위 식에서 제외시키면 섭동장으로 이루어진 미분 방정식은 식(8)이 되고 미분 방정식의 해를 구하면 식(9)가 나온다.

$\[ \frac{dx}{dt}=a\left(t\right)x \]$

(8)

$\[ x=\mathrm{e}\mathrm{x}\mathrm{p}\left(\int a\left(t\right)dt\right) \]$

(9)

미분 방정식의 해를 보면, a(t)에 따라 x가 기하급수적으로 변하는 것을 볼 수 있다. a(t)가 양의 값을 가지면 온도의 섭동 값인 x가 기하급수적으로 증가하며, a(t)가 음의 값을 가지면 x가 0으로 수렴하게 된다. 따라서, a(t)는 계절적 강제력 Q(t, T)에 따른 계절적 안정도를 나타내고 a(t)의 부호에 의해 지역이 계절별로 안정한지 불안정한지 판단할 수 있는 지표가 된다.

2.2.2 계절적 안정도[seasonal stability, a(t)]

2.2장에서 도출한 식(5)를 이용하여 계절적 안정도를 나타내는 a(t) 식을 구해볼 것이다.

$\[ \mathrm{\Delta }x=a\left(t\right)x\left(t\right)\mathrm{\Delta }t+N\left(t\right)\mathrm{\Delta }W+f\left(\tau \right)\mathrm{\Delta }t \]$

(10)

식(5)의 양 변에 Δt를 곱해준 뒤 Δx = x(t = Δt) - x(t)를 사용하고 브라운 입자(Brownian particle) ΔW = ξ(t)Δt로 정의하면 식(10)이 나온다. f(τ)는 계절에 대한 주기보다 더 긴 시간동안 천천히 변화하는 강제력이기 때문에, 계절에 따른 f(τ)는 거의 변화하지 않는다. 그러므로 f(τ)에 계절 평균을 취하면 거의 일정한 값을 가진다. 또한, ΔW는 평균이 0이며, 표준편차가 $$ \sqrt{\mathrm{\Delta }t}$$ 인정규분포를 따른다. 이러한 특징을 사용하기 위해 식(10)에서 양변에 x(t)를 곱하고 앙상블 평균해주면 식 (11)이 된다.

$\[ 〈x\left(t\right)x\left(t+\mathrm{\Delta }t\right)〉-⟨x^2\left(t\right)⟩=a\left(t\right)⟨x^2\left(t\right)⟩\mathrm{\Delta }t+〈f\left(\tau \right)x\left(\tau \right)〉\mathrm{\Delta }t \]$

(11)

여기서 계절에 대한 주기함수인 다른 항들과는 달리f(τ)는 느리게 변하는 요소이기 때문에 계절적 안정도를 나타내는 a(t)에 영향을 미치지 않는다. 그러므로 식(11)에서 f(τ)항을 무시하고 a(t)에 대해서 식을 정리하면 다음과 같은 식을 도출할 수 있다.

$\[ a\left(t\right)=\frac{1}{\mathrm{\Delta }t}\frac{〈x\left(t\right)x\left(t+\mathrm{\Delta }t\right)〉-⟨x^2\left(t\right)⟩}{⟨x^2\left(t\right)⟩} \]$

(12)

우리는 1년을 주기로 생각하는 모델을 구성했기 때문에 이 식에서 $$ \mathrm{\Delta }t=\frac{1}{12}$$가 된다. 이제 우리는 식(12)을 이용하여 계절적 안정도의 값을 직접적으로 구할 수 있다.

2.2.3 노이즈 크기[noise amplitude, N(t)]

노이즈의 크기를 나타내는 N(t)도 2.2장에서 도출한 단순화된 기후 모델 식(5)를 바탕으로 구할 수 있다. 식(10)에서 y(t) = x(t + Δt) - x(t) - a(t)x(t)Δt로 정의하면 다음과 같은 식이 된다.

$\[ y\left(t\right)=N\left(t\right)\mathrm{\Delta }{W}_t+f\left(\tau \right)\mathrm{\Delta }t \]$

(13)

여기서 계절적 주기에 영향을 주지 않는 장기 강제력의 항을 제거하기 위해 y(t + Δt) = N(t + Δt)ΔW_t+Δt + f(τ)Δt의 식을 이용한다. 이때 ΔW는 Brownian time step (Δt) 동안 움직인 브라운 입자이기 때문에 <ΔW²> = Δt가 되어 N(t)를 구하는 과정은 다음과 같다:

$\[ ⟨y^2\left(t\right)⟩=N^2\left(t\right)\mathrm{\Delta }t+f^2\left(\tau \right)\mathrm{\Delta }{t}^2 \]$

(14)

$\[ 〈y\left(t\right)y\left(t+\mathrm{\Delta }t\right)〉\simeq f^2\left(\tau \right)\mathrm{\Delta }{t}^2 \]$

(15)

$\[ ⟨y^2\left(t\right)⟩-〈y\left(t\right)y\left(t+\mathrm{\Delta }t\right)〉\simeq N^2\left(t\right)\mathrm{\Delta }t \]$

(16)

$\[ N\left(t\right)=\sqrt{\frac{1}{\mathrm{\Delta }t}\left(⟨y^2\left(t\right)⟩-〈y\left(t\right)y\left(t+\mathrm{\Delta }t\right)〉\right)} \]$

(17)

식(15)의 경우 자기상관(auto-correlation)과 관련성이 있기 때문에, 시간 척도가 달라 관련성이 없다고 판단하는 다른 항들은 무시할 수 있다. 또한 N(t)N(t + Δt)ΔW_tΔW_t+Δt 항은 브라운 모션의 정의에 따라서 앙상블 평균은 0이 된다(<ΔW_tΔW_t+Δt> = 0) 하지만 f(τ)의 경우에는 계절에 따른 변화가 거의 존재하지 않아 Δt의 시간이 지나도 거의 동일한 값을 가진다고 가정하여 f²(τ)Δt²만 남게 되는 것이다.

Figure 1은 3월 남극의 a(t)를 나타내는 그래프로 남극 대륙 주변에서 불안정함이 나타나는 것을 볼 수 있다. 불안정한 지역 중 임의로 4개의 지역을 선정했으며, 해당 지역들은 이후 그래프에서도 계속 사용될 것이다.

Fig. 1.

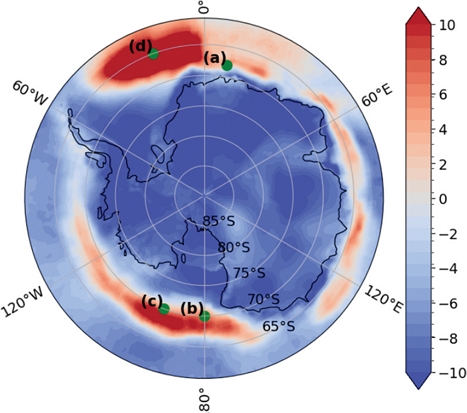
The region used in this study was selected as an unstable area in March, late summer in Antarctica. The selected area was marked on a map. (a) longitude: 10, latitude: -68 (b) longitude: 180, latitude: -70 (c) longitude: 200, latitude: -70 (d) longitude: 340, latitude: -65.

Figure 2는 식(12)로 계산된 안정도 a(t)와 식(17)로 계산된 노이즈의 크기 N(t)를 보여주는 그래프이다. 이 그래프에 사용된 지역들은 남극의 늦여름인 3월에 불안정한 모습을 보이는 지역으로, Fig. 1에서 점으로 표시한 지역이다. Figure 2를 통해 남극의 여름철에 a(t)가 양수 값을 가지는 것을 볼 수 있다. 이러한 여름철의 불안정이 누적됨에 따라, 불안정의 영향이 늦여름까지 영향을 끼치며 안정한 상태로 전환될 때 안정도가 최대 분산을 가지는 “기억 효과(memory effect)”가 발생한다. 반대로, 안정한 상태에서 불안정한 상태로 전환되는 순간, 안정도는 최소 분산을 가지게 된다. 겨울철 N(t)가 큰 값을 가지는 것은 적도와 극의 온도차이가 심해져 저기압의 강도가 강해지기 때문이다. 이에 대한 추가적인 설명은 결과 부분에서 다룰 것이다.

Fig. 2.

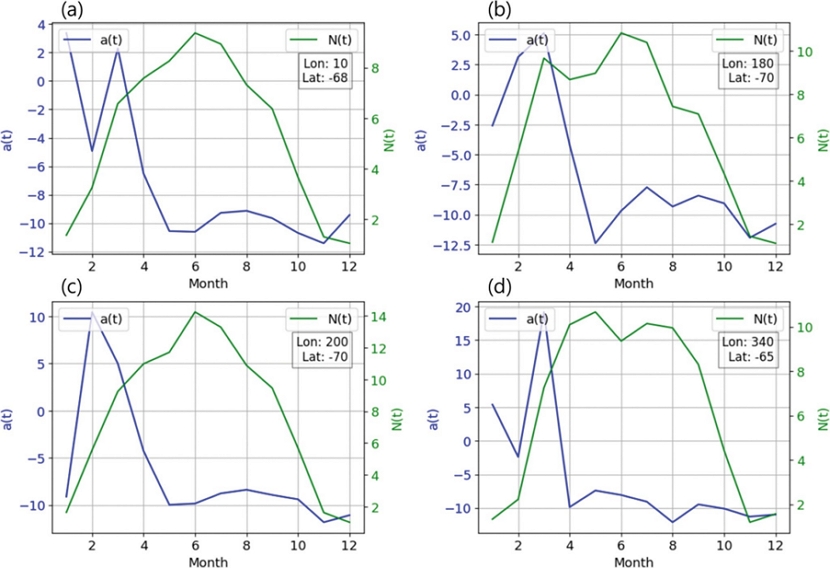
We make a seasonal comparison of stability a(t) and noise amplitude N(t) in unstable areas of Antarctica. Each figure is a graph drawn from the following location information: (a) longitude: 10, latitude: -68, (b) longitude: 180, latitude: -70, (c) longitude: 200, latitude: -70, (d) longitude: 340, latitude: -65. The blue line and the left y-axis represent a(t), while the green line and the right y-axis represent N(t). In summer (January~April), a(t) has a positive value due to several feedback effects such as sea ice albedo feedback and Arctic amplification, which means it is unstable. In winter (About June), N(t) has a maximum value because the temperature difference between the equator and the poles is maximum and the intensity of low pressure is strong.

2.2.4 장기 강제력[long-term forcing, f(τ)]과 장기 강제력의 영향(long-term effect)

장기 강제력이 모델에 포함되었을 때, 해양과 지구온난화 같이 천천히 변하는 요소가 포함되어 있어 계절적 변동성을 정확히 묘사하지 못하는 결과가 나왔다. 따라서 우리는 장기 강제력의 영향을 직접적으로 구하여 온도자료에서 장기 강제력의 영향력을 제거한 후, 계절적 변동성에 영향을 주는 항으로만 모델을 구성하려 한다.

먼저, 식(10)을 이용하여 장기 강제력을 구할 수 있다. N(t)ΔW는 앞서 설명한 것처럼 가우시안 입자인 ΔW가 정규분포를 따르기에 평균을 취하면 0이 되므로 생략된다. 또한 f ≡ f(τ)Δt라 정의하면, 다음과 같은 식으로 장기 강제력 f를 구할 수 있다:

$\[ f=\overline{x\left(t+\mathrm{\Delta }t\right)-x\left(t\right)-a\left(t\right)x\left(t\right)\mathrm{\Delta }t} \]$

(18)

앞서 계절적인 시간 척도를 나타내었던 t와 달리 τ는 보다 장기적인 시간 척도를 나타낸다. 따라서 f는 계절에 따른 변동이 거의 존재하지 않으므로 년 평균($$ \overline{ \cdot }$$)을 사용하여 값을 도출한다. 위와 같은 과정으로 구한 f에 $$ \frac{1}{\mathrm{\Delta }t}$$을 곱하여 f(τ)를 구하면 Fig. 3과 같은 결과가 나온다. Figure 3은 남극의 불안정한 지역을 대상으로 f(τ)의 시계열 그래프를 나타낸 것으로 시간에 따른 장기 강제력의 추이를 확인할 수 있다.

Fig. 3.

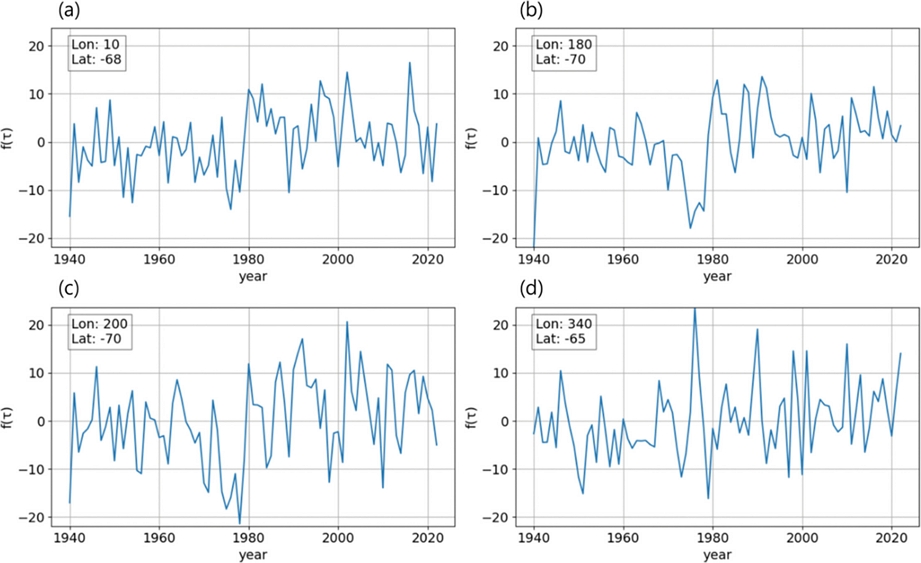
This time series distribution represents the long-term forcing f(τ) at a specific point in an unstable region of Antarctica. By analyzing the trend in long-term forcing, we can observe slow-evolving phenomena in this area. Each figure is a graph drawn from the following location information: (a) longitude: 10, latitude: -68, (b) longitude: 180, latitude: -70, (c) longitude: 200, latitude: -70, (d) longitude: 340, latitude: -65.

장기 강제력의 추이를 분석한 결과, 네 지역 모두에서 1980년대에 강제력이 급격히 상승하는 현상이 관찰되었다. 이 시기, 남극의 오존층이 대규모로 파괴되면서 강제력이 증가한 현상으로 해석할 수 있다. 1980년대에는 염불화탄소(CFCs)와 같은 인공 화학물질의 배출로 인해 오존층이 심각하게 손상되었다(Farman et al., 1985). 오존층은 대기 중에서 자외선을 흡수하여 지표면으로의 자외선 유입을 막는 역할을 하는데, 오존층이 얇아지면서 남극 지역에 더 많은 양의 자외선이 도달하게 되었다. 이러한 자외선 증가가 강제력 증가에 기여하였으며, 이는 장기 강제력 f(τ)의 급격한 상승으로 모델에 반영되었다.

장기 강제력뿐만 아니라, 장기 강제력의 계수를 구하여 각 지역의 안정도에 따라 장기 강제력이 어떻게 반응하는지 알 수 있다. 그 후 원래 데이터에서 장기 강제력의 영향을 제외시킬 수 있다. 따라서, 장기 강제력의 계수를 구하기 위해 먼저 식(5)의 미분방정식을 풀어 x(t)의 식으로 나타내 준다.

$\[ \begin{array}{c}x\left(t\right)=\text{exp}\left({\int }_0^{t}a\left(s\right)ds\right){\int }_0^{t}N\left(t^{\prime }\right)\text{exp}\left(-{\int }_0^{t^{\prime }}a\left(s\right)ds\right)d{w}^{\prime }\hfill \\ +\text{exp}\left({\int }_0^{t}a\left(s\right)ds\right){\int }_0^{t}f\left(\tau \right)\text{exp}\left(-{\int }_0^{t^{\prime }}a\left(s\right)ds\right)d{t}^{\prime }\hfill \end{array} \]$

(19)

위 식에서 f(τ)는 매우 천천히 변화하는 장기 강제력이기 때문에 상수로 취급하여 적분 밖으로 빼 주면 장기 강제력의 계수 $$ \mathrm{e}\mathrm{x}\mathrm{p}\left({\int }_0^{t}a\left(s\right)ds\right){\int }_0^t\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\int }_0^{t^{\prime }}a\left(s\right)ds\right)d{t}^{\prime }$$를 구할 수 있다. a(t)는 계절적 주기성을 가지므로 주기함수의 성질인 $$ t=nT+\tilde{t}$$을 사용하여 해당 적분을 계산할 수 있다(Moon and Wettlaufer, 2013). T는 1년을 의미하고, 임을 고려하여 양의 상수(floquet exponent) γ를 다음과 같이 정의할 수 있다:

$\[ \gamma \equiv -{\int }_0^{T}a\left(s\right)ds \]$

(20)

양의 상수 γ를 이용하여 장기 강제력의 계수를 계산하면 적분 과정은 식(21)과 식(22)와 같다. 장기 강제력 계수의 계산 과정을 보다 쉽게 표현하기 위해 식(21)과 식(22)로 나누어 설명하였다:

$\[ \begin{array}{c}\text{exp}\left({\int }_0^{t}a\left(s\right)ds\right)=\text{exp}\left(n{\int }_0^{T}a\left(s\right)ds+{\int }_0^{\tilde{t}}a\left(s\right)ds\right)\hfill \\ =e^{-n\gamma }\text{exp}\left({\int }_0^{\tilde{t}}a\left(s\right)ds\right)\hfill \end{array} \]$

(21)

$\[ \begin{array}{c}{\int }_0^t\text{exp}\left(-{\int }_0^{t^{\prime }}a\left(s\right)ds\right)d{t}^{\prime }=e^{n\gamma }{\int }_0^{\tau }\text{exp}\left(-{\int }_0^{t^{\prime }}a\left(s\right)ds\right)d{t}^{\prime }\hfill \\ +\frac{e^{n\gamma }-1}{e^{\gamma }-1}{\int }_0^T\text{exp}\left(-{\int }_0^{t^{\prime }}a\left(s\right)ds\right)d{t}^{\prime }\hfill \end{array} \]$

(22)

식(22)는 Moon and Wettlaufer (2013)의 방법을 사용하여 전개하였다. 따라서 최종적으로 장기 강제력의 계수를 구하는 식은 (23)이 된다:

$\[ \begin{array}{c}\text{exp}\left({\int }_0^{t}a\left(s\right)ds\right){\int }_0^t\text{exp}\left(-{\int }_0^{t^{\prime }}a\left(s\right)ds\right)d{t}^{\prime }\hfill \\ =\text{exp}\left({\int }_0^{\tilde{t}}a\left(s\right)ds\right)\left\{{\int }_0^t\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\int }_0^{t^{\prime }}a\left(s\right)ds\right)d{t}^{\prime }\right.\hfill \\ \left. +\frac{1-e^{-\gamma n}}{e^{\gamma }-1}{\int }_0^T\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\int }_0^{t^{\prime }}a\left(s\right)ds\right)d{t}^{\prime }\right\}\hfill \end{array} \]$

(23)

식(23)을 식(19)의 장기 강제력 계수에 대입한 뒤 좌변으로 이동시켜 원 데이터 x(t)에서 장기 강제력의 영향을 배제시킬 수 있다.

$\[ \begin{array}{c}x\left(t\right)-f\left(\tau \right)\text{exp}\left({\int }_0^{\tilde{t}}a\left(s\right)ds\right)\left\{{\int }_0^{\tau }\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\int }_0^{t^{\prime }}a\left(s\right)ds\right)d{t}^{\prime }\right.\hfill \\ \left. +\frac{1-e^{-\gamma n}}{e^{\gamma }-1}{\int }_0^T\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\int }_0^{t^{\prime }}a\left(s\right)ds\right)d{t}^{\prime }\right\}\hfill \\ =\text{exp}\left({\int }_0^{t}a\left(s\right)ds\right){\int }_0^{t}N\left(t^{\prime }\right)\text{exp}\left(-{\int }_0^{t^{\prime }}a\left(s\right)ds\right)d{w}^{\prime }\hfill \end{array} \]$

(24)

식(24)의 좌변을 보면 원래 데이터인 x(t)에서 장기 강제력 f(τ)와 그 계수를 곱한 항을 빼 줌으로써 장기 강제력의 영향을 배제시킬 수 있다. 이러한 과정으로 장기 강제력의 영향을 제외한 온도 데이터를 활용하여 계절적 변동성을 재현하는 통계적 모델링을 진행한다.

2.3 통계적 모델링(stochastic model)

최종적으로 우리가 위와 같은 과정으로 구한 a(t), N(t) 그리고 f(τ)의 영향을 뺀 x(t)로 식(10)을 바탕으로 다음과 같은 식을 통해 확률적 모델링(stochastic modeling)을 진행한다:

$\[ x_{n+1}=\left(1+a_n\mathrm{\Delta }t\right)x_n+N_n\mathrm{\Delta }W \]$

(25)

여기서 ΔW는 날씨에 의해 발생하는 노이즈로, 무작위 변수(random value)를 사용하여 날씨의 영향을 고려해준다. 식(25)의 x_n는 2.2.4장에서 소개한 방법으로 장기 강제력의 영향을 제외시켰기 때문에 식(10)에서 f를 제외하여 모델링 식을 건설하였다. 이 모델을 반복하여 x_n+1 의 값과 월별 표준편차를 도출한 뒤, 모델에서 얻어진 표준편차와 실제 온도 데이터의 표준편차를 비교함으로써 모델이 재분석 자료의 통계적 특성을 잘 묘사하는지 파악할 수 있다.

Figure 4는 식(25)를 적용하여 남극의 불안정한 지역을 대상으로 수행한 시뮬레이션 결과를 보여준다. 본 연구의 목적은 원래 자료의 통계적 특성을 재현하는 통계적 모델링을 진행하는 것이기 때문에, 무작위 변수를 사용하여 개별 값을 시뮬레이션한 결과인 Fig. 4는 t2m 재분석 자료의 개별 값을 정확히 묘사하지 않는다.

Fig. 4.

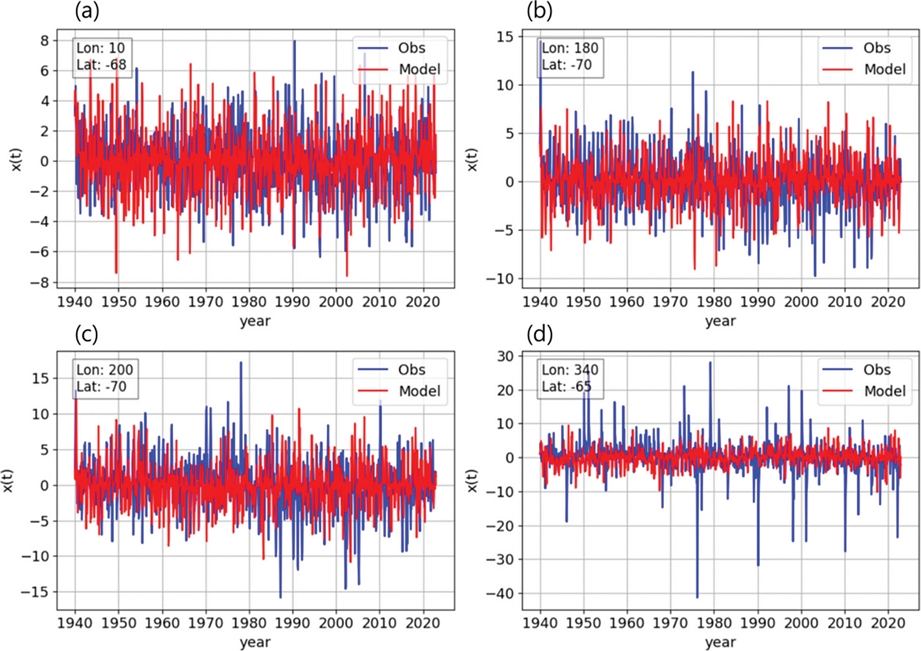
The time series method applies to 83 years of monthly-averaged ERA5 2m air temperature data from 1940 to 2022. Each figure is a graph drawn from the following location information: (a) longitude: 10, latitude: -68, (b) longitude: 180, latitude: -70, (c) longitude: 200, latitude: -70, (d) longitude: 340, latitude: -65. The simulation results (red) from the statistical model using our time series analysis method are compared with the original time series of air temperature anomalies (blue). This graph is a simulation result of individual values using random variables, so it does not accurately depict the individual values of the reanalysis data.

Figure 5는 앙상블 시뮬레이션을 활용한 통계적 분석의 결과를 나타낸다. 앙상블 시뮬레이션은 복잡한 시스템을 분석하기 위해 여러 번의 시뮬레이션을 시행하여 종합적으로 분석하는 기법으로, 앙상블 시뮬레이션을 진행한 뒤 통계적 분석을 통해 모델에 대한 신뢰도를 검증할 수 있다. 앙상블 시뮬레이션을 진행할 때 시뮬레이션 횟수가 늘어날수록 샘플의 개수가 많아지게 되며, 많은 샘플을 바탕으로 진행하는 통계적 분석의 결과는 원래 자료의 통계량을 보다 잘 재현하게 된다. 이를 바탕으로 Fig. 5에서는 시뮬레이션 횟수를 원래 자료의 시계열 길이보다 더 길게 설정하여 보다 많은 샘플을 바탕으로 통계량을 비교하였다. 그 결과, 모델의 통계량이 재분석 자료의 통계량을 거의 정확히 묘사함을 확인할 수 있다. 이를 통해 본 연구의 방법론 및 통계적 모델링의 신뢰성을 검증할 수 있었다. 또한, 통계적 모델링을 적용한 지역이 불안정하며 노이즈의 크기가 큰 지역임에도 불구하고, 모델이 통계적 특성을 잘 재현함으로써, 본 연구의 통계 모델이 안정도와 상관없이 다양한 지역에 적용 가능함을 판단할 수 있었다.

Fig. 5.

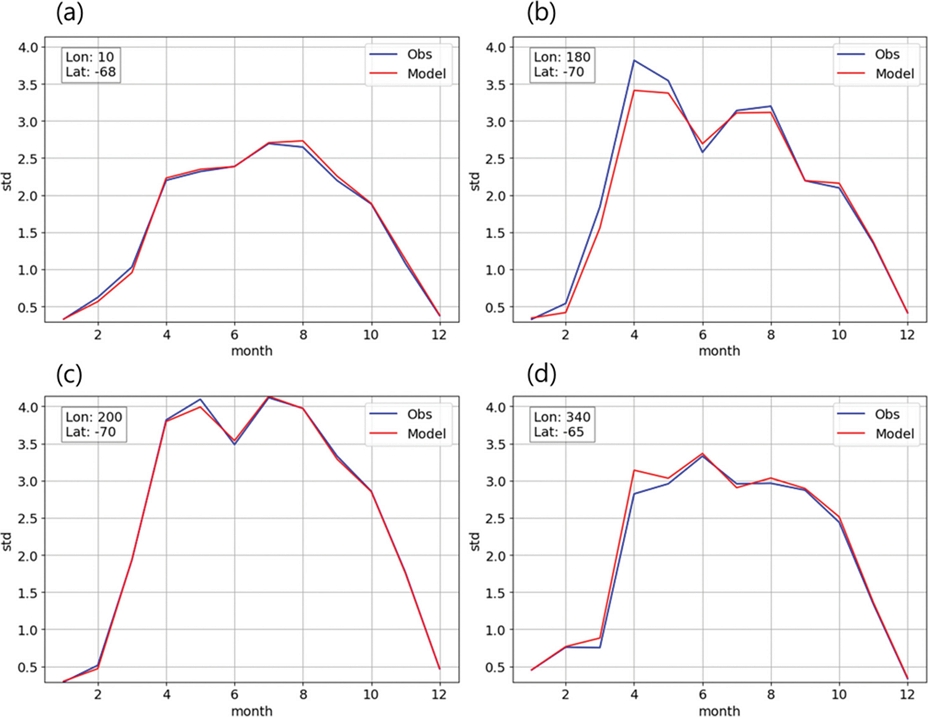
Seasonal standard deviations of the probabilistic model (red) are compared with the original data (blue). Each figure is a graph drawn from the following location information: (a) longitude: 10, latitude: -68, (b) longitude: 180, latitude: -70, (c) longitude: 200, latitude: -70, (d) longitude: 340, latitude: -65. The ensemble simulation technique was used to increase the number of simulations and perform statistical analysis based on a larger number of samples. In addition, the modeling was performed after removing the influence of long-term forcing that had no seasonal effect from the original data. As a result, the model shows excellent performance and closely matches the statistical characteristics of the original data.

3. 결 과

2.2장에서 도출한 방법을 통해 안정도 a(t)를 구해보면 전 지역의 안정성 여부를 알 수 있다. 음의 안정도를 가지는 지역은 안정한 상태로, 외부 요인에 의해 변동이 생기더라도 다시 원래 상태로 돌아가는 성질을 가진다. 반면 양의 안정도를 가지는 지역은 불안정한 상태로, 외부 요인에 의해 변동이 생기면 변화의 정도보다 더 크게 원래 상태에서 멀어지는 양의 피드백(positive feedback)의 성질을 보인다.

전 지구 월별 a(t) 그래프인 Fig. 6를 통해 엘니뇨-남방진동(El Niño-Southern Oscillation, ENSO), 대서양 니뇨(Atlantic Niño), 인도양 쌍극자(Indian OceanDipole, IOD) 등 다양한 기후 현상을 확인할 수 있다. 가장 뚜렷하게 불안정이 나타나는 기후 현상은 sea ice albedo feedback이다. 여름철에 태양 복사 에너지가 극지역에 입사하면서, 얇게 형성된 해빙의 가장자리 부분부터 녹아 알베도(albedo)가 감소하고, 그로 인해 더 많은 태양 복사 에너지가 입사하는 sea ice albedo feedback이 발생한다(Curry et al., 1995). 해당 피드백 작용으로 여름철 극지방 해빙의 가장자리 부분은 매우 불안정한 모습을 보인다(Figs. 6a, c).

Fig. 6.

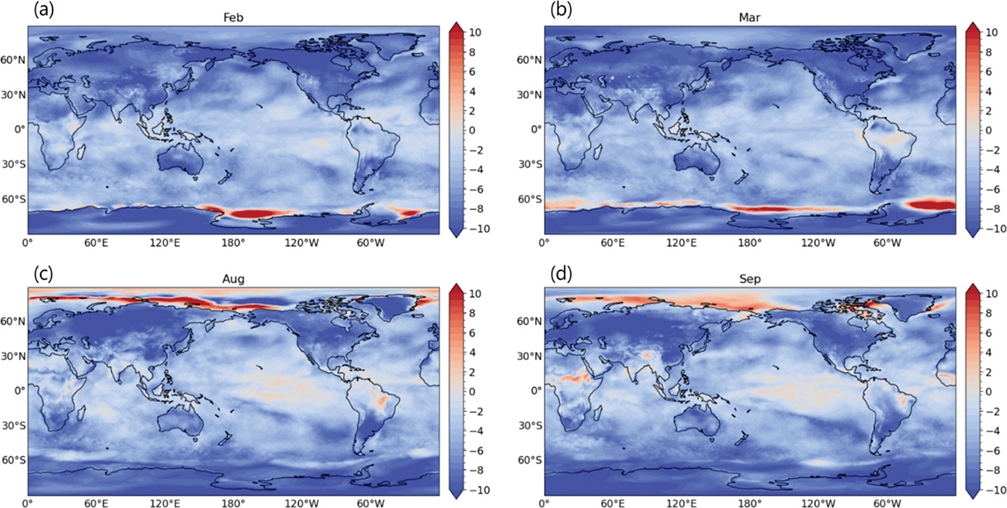
The seasonal variability of stability a(t) can be observed, where a(t) is a function of latitude and longitude. In polar summers and late summers, instability is evident at the edge of sea ice. (a) February (summer of the Antarctic), (b) March (late summer of the Antarctic), (c) August (summer of the Arctic), and (d) September (late summer of the Arctic).

그러나 남극의 3월(Fig. 6b), 북극의 9월(Fig. 6d)처럼 늦여름에는 앞서 설명한 sea ice albedo feedback과는 다른 AA와 관련된 불안정성이 나타난다. AA는 극지방에서의 기후 변화가 전 지구적 평균보다 빠르게 진행되는 현상이며(Serreze and Barry, 2011) 최근들어 그 강도가 강해지고 있어 극 지역의 기후를 이해하는데 필수적이다(Rantanen et al., 2022). AA는 sea ice albedo feedback뿐만 아니라 온도, 해빙, 대기 조건, 해양 등 다양한 메커니즘에 영향을 받지만(Previdi et al., 2021) 특히 여름 동안 해빙이 손실되면서 알베도가 감소하여 늦여름에 강한 AA가 발생하게 된다. Figures 6b, d를 통해 늦여름 AA에 의해 발생하는 극지역의 불안정을 확인할 수 있으며, AA에 의한 불안정의 형태가 남극과 북극에서 차이가 있음을 알 수 있다. 남극은 북극에 비해 두꺼운 육빙과 주변에 넓은 해양이 존재하기 때문에 늦여름인 3월에 해빙의 가장자리에서만 AA에 의한 불안정이 나타난다. 반면, 북극의 경우에는 지구 온난화로 해빙의 두께가 감소하고 있기 때문에 늦여름인 9월에 해빙의 가장자리부터 넓은 지역에서 AA에 의한 불안정이 나타난다(Vaughan et al., 2013). 이러한 극의 불안정은 극지역의 생태계를 위협할 뿐만 아니라 전 지구적으로 영향을 미칠 수 있다.

N(t)는 날씨와 관련된 노이즈로, 특히 저기압의 강도와 관련이 있다. Figures 7a-b 를 통해 겨울철 중∙고위도 지역에서 N(t)의 강도가 높게 나타나는 경향을 볼 수 있다. 이는 여러가지 요인으로 인해 겨울철 중∙고위도 지역에 저기압이 형성되기 때문이다(Rasmussen, 2003). 겨울철 남북의 기온차의 증가는 경압불안정(baroclinic instability)를 강화시킨다. 이는 날씨의 강도를 높여주는 효과로 통계 모델에서 노이즈의 강도를 증가시킨다.

Fig. 7.

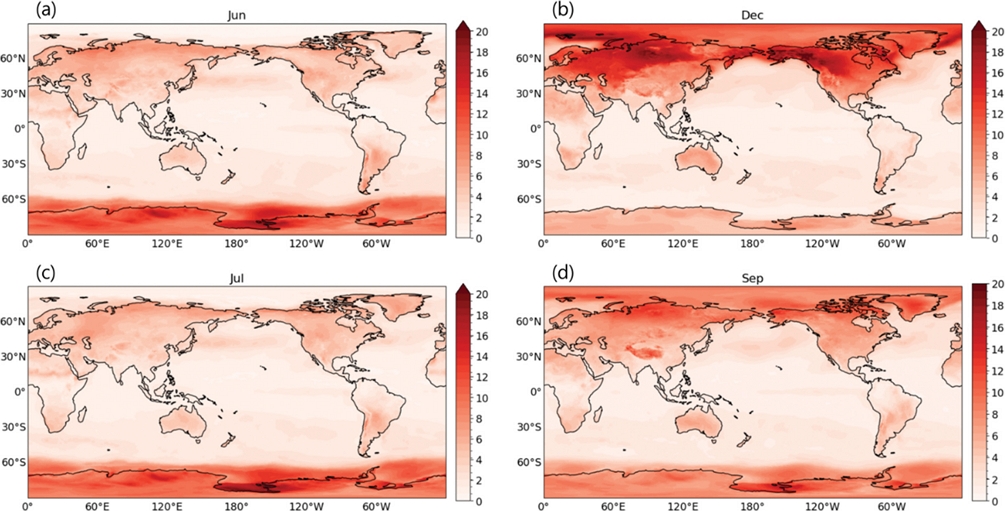
The seasonal variability of the noise amplitude N(t) is represented as a function of latitude and longitude. (a) June, the winter of Antarctica. (b) December, the winter of the Arctic. (a), (b) Strong N(t) appears due to extreme low pressure in winter. (c) In July, the summer of the Northern Hemisphere, there is the influence of storm tracks stretching from the Western Pacific to the Eastern Pacific. (d) In September, strong N(t) occurs due to a strong low-pressure system over the Tibetan Plateau.

Figures 7a, c, and d를 통해 날씨와 관련된 다양한 기후 이벤트를 확인할 수 있다. 6월과 7월의 N(t) 그래프(Figs. 7a, c)를 보면 우리나라 주변 북태평양 지역에서 동서로 이어지는 폭풍 경로(storm track)의 영향을 볼 수 있다. 또 9월의 N(t) 그래프(Fig. 7d)를 보면 티베트 고원에서 강한 N(t)가 관찰되는데, 이는 높은 산악 지형과 제트기류의 상호작용으로 인해 저기압이 형성되기 때문이다.

장기 강제력 f(τ)는 지구온난화와 해양의 변화와 같은 느리게 진행되는 현상을 확인할 수 있다. Figure 8에서는 강력한 엘니뇨(El Niño)와 라니냐(La Niña)가발생했던 특정 연도의 전 지구 f(τ) 분포를 보여준다. 먼저, 엘니뇨가 발생한 1982년(Fig. 8a)과 2015년(Fig. 8c)을 보면 동태평양에서 양의 강제력이 나타난다. 이는 엘니뇨로 인해 무역풍이 약화되고, 그 결과 동태평양의 온도가 상승한 현상을 반영한 것이다. 반면, 라니냐가 발생한 1988년(Fig. 8b)과 2021년(Fig. 8d)에서는 무역풍이 강화됨에 따라 동태평양의 해수 온도가 하강하여, 음의 강제력이 나타났다.

Fig. 8.

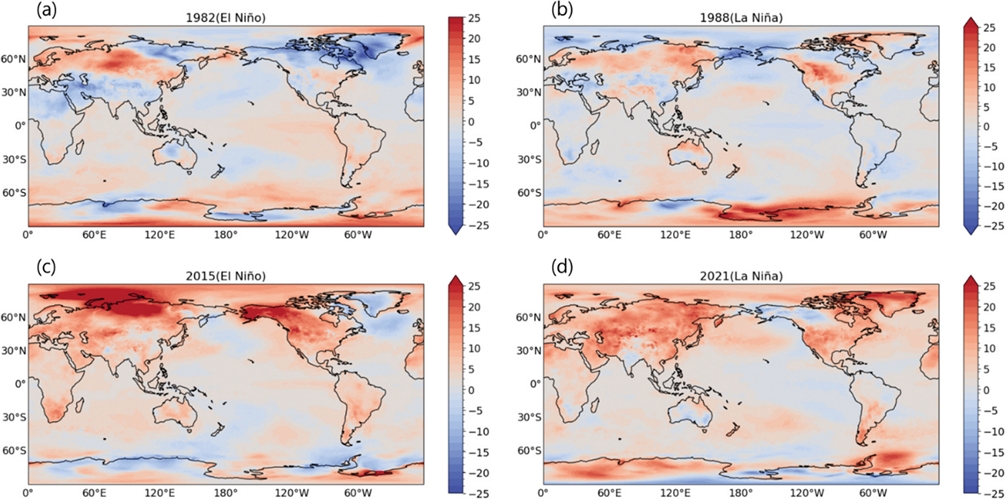
The long-term forcing, f(τ), is a function of latitude and longitude and changes slowly over extended periods, resulting in an annual average value for each year. The year used in the figure is the year when a special El Niño La Niña event occurred. (a) the strong El Niño event in 1982 (Nino 3.4 index 2.3), (b) the strong La Niña event in 1988 (Nino 3.4 index -2.29), (c) the strong El Niño event in 2015 (Nino 3.4 index 2.81), (d) the strong La Niña event in 2021 (Nino 3.4 index -1.26).

또한 Fig. 8을 통해 지구온난화의 영향을 확인할 수 있다. 1980년대의 Figs. 8a, b와 비교하여, 최근인 Figs. 8c, d에서는 지구온난화로 인해 전반적으로 높은 f(τ) 값을 가진다. 특히 2015년(Fig. 8c)에는 북극 지역에서 강한 강제력이 나타나는 것을 볼 수 있다. 1982년의 엘니뇨와 1988년의 라니냐는 거의 반대되는 분포를 보이는 반면, 2015년의 엘니뇨와 2021년의 라니냐는 높아진 f(τ) 값으로 인해 반대 분포가 뚜렷하게 나타나지 않았다. 따라서 전 지구적 f(τ) 분포를 통해 엘니뇨와 라니냐 같은 해양의 변동 및 지구온난화와 같은 기후 변화의 영향을 효과적으로 확인할 수 있다.

4. 결 론

본 연구에서는 ERA5 재분석 자료의 온도 자료를 활용하여 계절적 안정도 a(t), 날씨와 관련된 노이즈 N(t), 장기 강제력 f(τ)와 그 계수를 분석하고 이를 기반으로 한 통계적 모델을 구축하였다. 또한 안정도, 노이즈, 장기 강제력 모두 수식을 통해 값을 직접 구할 수 있기 때문에 전 지구 모든 지역에 적용할 수 있다는 점에서 큰 의의를 가진다.

계절적 안정도 a(t)를 통해 지역/계절별 민감도를 파악할 수 있었다. a(t)가 양의 값을 가지면 불안정한 상태로 강제력에 민감하게 반응하는 반면, 음의 값을 가지면 안정한 상태로 강제력에 민감하게 반응하지 않고 원래의 상태를 유지하려는 성질을 가진다. 계절적 안정도를 분석한 결과, 여름철 극지역에서는 sea ice albedo feedback으로 인한 불안정성이 나타났으며, 늦여름에는 해빙의 가장자리부터 AA에 의한 불안정이 확인되었다. 또한 ENSO(엘니뇨-남방진동), Atlantic Niño, IOD(인도양 쌍극자) 등과 같은 기후 현상도 확인할 수 있었으며, 안정도가 양의 값을 가지는 기간동안 불안정성이 누적되어 안정한 상태로 전환되는 시점에 최대 분산을 가지는 “기억효과”가 나타났다.

N(t)는 날씨와 관련된 노이즈를 나타내는 변수로, 적도와 극의 온도 차이가 가장 큰 겨울철에 저기압의 강도가 증가하면서 극 저기압이 발생해 남극의 겨울철 N(t) 값이 최대에 도달하는 것을 확인하였다. 또한, 전 지구 N(t) 그래프를 통해 동아시아 인근의 폭풍 경로와 티베트 고원에서 저기압이 나타나는 것을 확인할 수 있었다.

장기 강제력 f(τ)는 오랜 시간에 걸쳐 진행되는 현상들을 나타내는 변수로, 이를 통해 엘니뇨, 라니냐와 같은 해양 변동과 지구온난화와 같은 기후 변화를 분석할 수 있었다. 엘니뇨 발생 시 동태평양에서 양의 강제력이, 라니냐 발생 시에는 음의 강제력이 나타나는 것을 확인하였으며, 1980년대와 최근의 f(τ) 분포를 비교한 결과, 전반적으로 증가한 f(τ)가 확인되었다.

본 연구에서 구축한 통계적 모델은 재분석 자료의 통계량을 거의 정확하게 반영하는 결과를 보였다. 통계적 모델링을 진행할 때, 장기 강제력의 영향을 제외하여 우리가 보고자 하는 계절적인 변동성을 잘 반영할 수 있었다. 또한 날씨의 영향을 반영하기 위해 무작위 값인 백색 노이즈(white noise)을 포함하고 모델링을 진행한 지역이 남극의 불안정 지역이었음에도 재분석 자료의 통계적 특성을 잘 재현할 수 있었다. 이러한 결과는 본 연구의 방법론이 신뢰할 수 있음을 증명하며, 제시된 방법론을 통해 주파수 중복성의 위험을 피하면서도 전 지구에 대한 계절적 안정도와 노이즈 크기, 장기 강제력의 값을 도출하여 순환 정적 시계열을 효과적으로 분석할 수 있음을 보여준다.

Acknowledgments

이 논문은 부경대학교 자율창의학술연구비(2022년)에 의하여 연구되었음.

References

• Bell, B., and Coauthors, 2021: The ERA5 global reanalysis: Preliminary extension to 1950. Quart. J. Roy. Meteor. Soc., 147, 4186-4227. [https://doi.org/10.1002/qj.4174]
• Berger, A., 1978: Long-term variations of daily insolation and Quaternary climatic changes. J. Atmos. Sci., 35, 2362-2367. [https://doi.org/10.1175/1520-0469(1978)035<2362:LTVODI>2.0.CO;2]
• Curry, J. A., J. L. Schramm, and E. E. Ebert, 1995: Sea ice-albedo climate feedback mechanism. J. Climate, 8, 240-247. [https://doi.org/10.1175/1520-0442(1995)008<0240:SIACFM>2.0.CO;2]
• Farman, J. C., B. G. Gardiner, and J. D. Shanklin, 1985: Large losses of total ozone in Antarctica reveal seasonal ClO_x/NO_x interaction. Nature, 315, 207-210. [https://doi.org/10.1038/315207a0]
• Gardner, W. A., 1991: Exploitation of spectral redundancy in cyclostationary signals. IEEE Signal processing magazine, 8, 14-36. [https://doi.org/10.1109/79.81007]
• Gardner, W. A., 1994: An introduction to cyclostationary signals. Cyclostationarity in Communications and Signal Processing, IEEE Press, 1-90.
• Hersbach, H., and Coauthors, 2020: The ERA5 global reanalysis. Quart. J. Roy. Meteor. Soc., 146, 1999-2049. [https://doi.org/10.1002/qj.3803]
• Kim, K.-Y., G. R. North, and J. Huang, 1996: EOFs of one-dimensional cyclostationary time series: Computations, examples, and stochastic modeling. J. Atmos. Sci., 53, 1007-1017. [https://doi.org/10.1175/1520-0469(1996)053<1007:EOODCT>2.0.CO;2]
• Milankovitch, M. K., 1941: Kanon der Erdbestrahlung und seine Anwendung auf das Eiszeitenproblem. Royal Serbian Academy Special Publication, 133, 1-633.
• Moon, W., and J. S. Wettlaufer, 2013: A stochastic perturbation theory for non-autonomous systems. J. Math. Phys., 54, 123303. [https://doi.org/10.1063/1.4848776]
• Moon, W., and J. S. Wettlaufer, 2017: A unified nonlinear stochastic time series analysis for climate science. Sci. Rep., 7, 44228. [https://doi.org/10.1038/srep44228]
• Mudelsee, M., 2019: Trend analysis of climate time series: A review of methods. Earth Sci. Rev., 190, 310-322. [https://doi.org/10.1016/j.earscirev.2018.12.005]
• Previdi, M., K. L. Smith, and L. M. Polvani, 2021: Arctic amplification of climate change: a review of underlying mechanisms. Environ. Res. Lett., 16, 093003. [https://doi.org/10.1088/1748-9326/ac1c29]
• Rantanen, M., A. Y. Karpechko, A. Lipponen, K. Nordling, O. Hyvarinen, K. Ruosteenoja, T. Vihma, and A. Laaksonen, 2022: The Arctic has warmed nearly four times faster than the globe since 1979. Commun. Earth Environ., 3, 168. [https://doi.org/10.1038/s43247-022-00498-3]
• Rasmussen, E. A., 2003: Polar lows. In A half century of progress in meteorology: A tribute to richard reed, Meteor. Monogr., 61-78. [https://doi.org/10.1007/978-1-878220-69-1_4]
• Serreze, M. C., and R. G. Barry, 2011: Processes and impacts of Arctic amplification: A research synthesis. Global Planet. Change, 77, 85-96. [https://doi.org/10.1016/j.gloplacha.2011.03.004]
• Vaughan, D. G., and Coauthors, 2013: Observations: cryosphere. Cambridge University Press, Climate change, 317-382. [https://doi.org/10.5167/uzh-104510]