동아시아 여름철 대기의 강 단기 예측성 검증
Abstract
Atmospheric rivers (ARs) are closely related to local precipitation which can be both beneficial and destructive. Although several studies have evaluated their predictability, there is a lack of studies on East Asian ARs. This study evaluates the prediction skill of East Asian ARs in the Korean Integrated Model (KIM) for 2020~2022 summer. The spatial distribution of AR frequency in KIM is qualitatively similar to the observation but overestimated. In particular, the model errors greatly increase along the boundary of the western North Pacific subtropical high as the forecast lead time increases. When the prediction skills are quantitatively verified by computing the Anomaly Correlation Coefficient and Mean Square Skill Score, the useful prediction skill of daily AR around the Korean Peninsula is found up to 5 days. Such prediction limit is primarily set by the wind field errors with a minor contribution of moisture distribution errors. This result suggests that the improved prediction of atmospheric circulation field can improve the prediction of East Asian summer ARs and the associated precipitation.
Keywords:
Atmospheric rivers, East Asian summer, Korean integrated model, Prediction skill1. 서 론
대기의 강(Atmospheric River, AR)은 좁고 긴 띠의 형태로 이루어지는 조직화된 수증기 수송 현상이다(Gimeno et al., 2016). 초기 AR 연구(Newell et al., 1992; Zhu and Newell, 1994, 1998)에서 미국 서부 산악 지형에 상륙한 AR이 극한 강수와 밀접한 관련이 있다는 사실이 알려지며 AR은 폭발적인 관심을 받기 시작했다. 미국 서부 및 유럽을 중심으로 시작된 AR연구는(Ralph et al., 2006; Lavers et al., 2011; Ralph and Dettinger, 2012; Dettinger, 2013; Lavers and Villarini, 2013, 2015) 동아시아, 남반구, 극지역 등을 비롯하여 점차 다양한 지역으로 확대 되었다(Kamae et al., 2017a; Nayak and Villarini, 2017; Paltan et al., 2017; Nash et al., 2018; Dhana Laskhmi and Satyanarayana, 2020; Shu et al., 2021). 이러한 연구들은 AR이 홍수 및 극한 강수와 같은 재해와 관련이 있기도 하지만 가뭄의 종식과 수자원 관리에도 중요한 역할을 함을 강조하고 있다.
최근에는 AR과 관련한 수문학적 위험성 및 유익성을 예측하려는 시도가 이어지고 있다. Wick et al. (2013)은 미국 서부 해안 지역에 인접한 동태평양 지역을 중심으로 AR의 발생과 상륙의 예측성을 평가하였으며, 예측기간이 길어질수록 AR 상륙의 예측성이 크게 떨어짐을 확인하였다. Nayak et al. (2014)는 미국 중부 지역에서의 AR 예측성을 평가하였고 AR 탐지에 이용하는 변수에 따라 예측성이 달라질 수 있음을 보고하였다. 또한 계절내-계절(Subseasonal-to-Seasonal, S2S) 시간 규모에서 AR의 예측성을 평가하려는 시도가 이루어 지기도 하였으며(DeFlorio et al., 2019), 해당 시간 규모에서 중요한 예측 인자로 사용되는 기후 모드를 활용하여 AR의 중장기 예측성 향상을 높이려는 노력도 이어지고 있다(Baggett et al., 2017; Mundhenk et al., 2018). 그러나 이러한 연구는 대부분 미국 혹은 동태평양 지역을 중심으로 진행되어왔다. 비록 DeFlorio et al. (2019)가 전 지구 규모에서 전반적인 AR의 예측성을 평가했지만 지역적 규모에서의 상세한 분석은 동태평양과 남태평양의 일부지역을 중심으로 이루어졌으며 아직까지 동아시아를 중심으로 한 AR 예측성 연구는 아직 부족한 실정이다(e.g., Tian et al., 2024).
동아시아는 AR의 수문학적 영향을 많이 받는 지역 중 하나이다. 동아시아 AR은 여름철에 가장 빈번하게 발생하며 이는 북서태평양 고기압의 확장이 특징적으로 나타나는 동아시아 여름 몬순의 영향임이 잘 알려져 있다(Mundhenk et al., 2016; Kamae et al., 2017a, b; Pan and Lu, 2020; Kim et al., 2021; Liang and Yong, 2021; Park et al., 2021; Kwon et al., 2022). 동아시아 여름철 AR은 강수와도 밀접한 관련이 있는데, Park et al. (2021)은 여름철 동아시아 강수의 약 35~70%가 AR을 동반하여 발생함을 보고하였다. 한반도 지역에 초점을 맞추어 AR의 강수 영향을 살펴본 Kwon et al. (2022)은 여름철 강수의 58%, 극한 강수의 62%가 AR의 영향을 받아 발생함을 보고하기도 하였다. 이와 같이 AR이 동아시아 여름철 강수 및 극한 강수에 큰 영향을 미치며 따라서 이 기간 동아시아 AR의 예측성을 잘 이해하는 것은 중요하다.
본 연구에서는 한국형수치예보모델(Korean Integrated Model, KIM)을 이용하여 동아시아 여름철 AR의 예측성을 평가하였다. KIM은 2011년부터 2019년까지 한국형수치예보모델개발사업단(Korea Institute of Atmopheric Prediction Systems, KIAPS)에서 개발한 전지구모델로(Hong et al., 2018) 2020년 4월부터 한국기상청에서 현업 운영하고 있는 수치모델이다. 현재 기상청에서 운영하고 있는 KIM 3.5 이상 버전은 초기 KIM 1.0 버전에서의 물리모수화를 업데이트하여 보다 개선된 강수 예측성을 보였고, 특히 2006년 7월 홍수와 같은 극한 강수를 정성적으로 잘 모의할 수 있는 것으로 알려져 있다(Hong et al., 2018). 이를 미루어 볼 때 AR 예측에 있어 KIM 모델을 충분히 활용할 수 있을 것으로 사료된다. 본 연구에서는 KIM을 이용하여 최근 3년(2020~2022년) 간의 동아시아 여름철 AR의 일 별 발생에 대해 예측기간 11일까지의 예측성을 평가하고 그 오차의 원인을 분석하였다. 2장에서는 KIM 모델에 대한 설명과 검증을 위해 사용한 자료 및 방법론에 대해 설명하고, 3장에서는 KIM 에서의 AR 발생 모의 능력과 예측성을 검증했으며 수증기 수지 분석을 통해 오차의 원인을 살펴보았다. 마지막으로 4장에서는 주요 결과를 요약하고 토의하였다.
2. 자료 및 방법
2.1 자료
AR 발생빈도를 확인하기 위해 유럽중기예보센터(European Center for Medium-range Weather forecast, ECMWF)에서 제공하는 ECMWF 재분석 자료 (ECMWF Reanalysis v5, ERA5) (Hersbach et al., 2020)를 이용하였다. ERA5의 수평해상도는 1.5o × 1.5o이며, 연직으로 37개 층이 있다. 분석을 위해 비습과 그리고 동서 및 남북방향 바람장을 사용하였다. 본 연구에서는 ERA5 재분석 자료와 KIM 모델을 비교하여 AR 모의능력을 평가하였다.
KIAPS에서 개발한 기상청 현업 모델 KIM은 하루에 2번 12시간마다(0000, 1200 UTC) 초기화되며 예측시간 84시간까지는 3시간 간격, 그 이후 288시간까지는 6시간 간격으로 약 12일까지의 예측장을 제공한다. 본 연구에서는 0000 UTC에 초기화된 예측장을 24시간 간격으로 사용하여 예측기간 0일부터 11일의 범위에서 AR의 발생빈도를 살펴보았다. 2020년부터 2022년까지의 여름철(6~8월) 초기장에서의 예측 결과를 분석 기간으로 설정하였다. KIM 모델의 수평해상도는 12 km 내외이며, 연직으로 91개의 층으로 이루어져있다. KIM 모델 모의 결과를 1.5o × 1.5o로 내삽하여 재분석자료와 수평해상도를 같도록 하였으며, 1000 hPa와 300 hPa, 그리고 이 사이의 7개 지위고도면 자료를 사용하였다(i.e., 1000, 950, 925, 850, 700, 600, 500, 400, 300 hPa).
2.2 AR 탐지 알고리즘
AR 탐지를 위해 Guan and Waliser (2015) 를 동아시아 실정에 맞게 수정한 Park et al. (2023) 알고리즘을 사용하였다. 해당 알고리즘은 연직 적분된 수증기 수송(Integrated water Vapor Transport, IVT)과 IVT 아노말리(IVT Anomaly, IVTA)를 이용하여 AR을 탐지하며, IVT는 식(1)과 같이 계산된다.
| (1) |
여기서 x, y는 각각 동서, 남북 방향의 단위 벡터, u, v는 각각 동서방향과 남북방향의 바람, q는 비습, g는 중력가속도이다. 또한 IVTA는 1979년부터 2022년까지의 재분석장 IVT 기후 값을 제거하여 계산된다. AR탐지를 위해 먼저 IVTA가 150 kg m-1 s-1 이상인 연속적인 격자의 집합을 AR 후보 객체로 선정한다. 이후 각 객체의 수증기 수송 방향을 고려하는 과정을 거치는데 객체 평균 IVT의 방향이 객체의 장축과 이루는 각도가 45o 이상이거나, 절반 이상의 격자에서 IVT가 객체 평균 IVT와 45o 이상의 각도를 갖는 객체를 제거한다. 이후 AR의 기하학적 정의를 고려하여 길이가 2000 km 이상이고 길이 대 너비의 비율이 2 이상인 객체만을 최종적으로 AR로 산출한다. 더 자세한 AR 탐지 과정은 Park et al. (2023)에서 확인 할 수 있다.
Park et al. (2023) 알고리즘이 IVTA를 통해 일차적으로 AR 후보 객체를 선정하는 것은 IVTA가 동아시아 여름 몬순 시기에 극한 강수의 특성을 잘 나타낸다는 점을 고려한 것이다. 또한 여름철 동아시아 몬순 순환에 동반되어 동서방향으로 길게 늘어져 발달하는 동아시아 AR을 잘 탐지하기 위하여 기존 Guan and Waliser (2015) 알고리즘에 있던 수증기의 북향수송에 대한 조건을 고려하지 않았다. Park et al. (2023) 알고리즘은 Guan and Waliser (2015) 알고리즘보다 동아시아 여름철 강수량과 AR 빈도수 사이의 관련성이 높음이 알려져 있다(Kim et al., 2023).
2.3 예측성 검증 평가 인자
KIM 모델의 예측기간에 따른 AR 발생빈도 예측성을 정량적으로 검증하기 위해 이상상관계수(Anomaly Correlation Coefficient, ACC)와 평균제곱 예측성(Mean Squared Skill Score, MSSS)을 예측성 평가인자로 사용하였다. 본 연구에서 AR 발생빈도(AR frequency)는 각 격자점에서 전체 분석기간 중 AR이 발생한 기간의 비율로 정의하였다. ACC는 모델의 예측결과 편차와 재분석 자료 편차의 선형 상관관계에 대한 예측성 진단 변수이며 식(2)와 같이 표현된다.
| (2) |
식(2)에서 t는 모델에서 예측하는 개별의 사례를 나타내며, 1부터 N의 범위를 가진다. N은 분석기간 동안의 총 초기화 예측횟수를 의미하며 본 연구에서는 2020~2022년 동안 여름철(6~8월)의 총 초기화 예측횟수인 276 (3년 × 92일)의 값을 갖는다. 또한, τ는 예측기간을 나타내며 KIM의 초기화 날짜로부터의 예측기간인 0일부터 11일의 범위를 가진다. M(t, τ)는 분석기간의 각 초기장에 따른 KIM 모델값을 나타내며, O(t, τ)는 M(t, τ)에 해당하는 기간에서의 관측값을 나타낸다. 각 예측기간에 따른 전체 초기화 날짜의 모델 아노말리와 관측 아노말리는 식(3)과 같이 정의된다.
| (3) |
여기서 C(t, τ)은 관측 기후값을 나타내며 본 연구에서는 1979~2022년 여름철 기후값에 해당한다.
모델의 예측 결과와 관측값이 완전히 일치하는 경우 ACC의 값은 1이다. 모델 모의 결과와 관측치 간의 선형적 상관성이 존재하지 않는 경우 ACC는 0이 된다. ACC를 예측성 평가 인자로 사용하는 경우 일반적으로 0.5부터 0.8까지의 값을 임계값으로 사용하며, 경험적으로 ACC가 0.6 이상의 값을 가질 때 예측성이 있다고 판단한다(Kim et al., 2018; Kataoka et al., 2020; Liu et al., 2021). 본 연구에서는 ACC의 값이 0.6에서 1 사이에 위치하는 경우에 예측성이 유의하다고 판단하였다.
MSSS은 식(4)의 관측에 대한 모델의 평균제곱오차(Mean Squared Error, MSE)와 식(5)의 관측 기후값에 대한 관측의 평균제곱오차의 비율로 이루어진 통계량이며 식(6)과 같이 나타낼 수 있다.
| (4) |
| (5) |
| (6) |
식(4)~(6)에서의 각 변수의 정의는 식(2)~(3)에서와 동일하다. MSSS는 모델의 예측결과와 관측값이 완전히 일치하는 완벽한 모델일 때(MSEM = 0) 1의 값을 갖는다. MSSS는 하한이 정해져 있는 ACC와 달리 모형의 평균제곱오차가 커질수록 하한 없이 감소할 수 있다. 본 연구에서는 MSEM와 MSEO이 일치할 때의 값인 0을 예측성 진단 기준으로 삼았으며, 해당 기준값은 모델의 오차와 관측의 변동성이 동일함을 의미한다(Song et al., 2018; Son et al., 2020; Hwang et al., 2020).
2.4 수증기 수지분석
수증기 수송 오차로부터 발생하는 AR의 예측 오차를 확인하기 위해 IVT의 수지분석을 진행하였다. 모델에서의 IVT 오차 원인을 살펴보기 위해 비습과 수평 바람을 각각 식(7)과 식(8)과 같이 관측(qobs, Vobs)과 오차 성분(q', V')으로 나누어 식(9)와 같이 모델의 IVT를 계산하였다.
| (7) |
| (8) |
| (9) |
여기서 q'Vobs은 모델의 비습 오차(q')에 의한 IVT 오차를 나타내고, qobsV'은 모델의 수평 바람 오차(V')에 의한 IVT 오차를 나타낸다. q'V'은 모델의 비습 오차(q')와 수평 바람 오차(V')의 곱에 의한 오차의 비선형항이다. 해당 항들을 비교하여 수증기 수송의 오차가 어떤 변수의 오차에 의해 크게 나타나는지 확인할 수 있다.
3. 결 과
3.1 KIM 모델의 AR 발생 모의 오차
Figure 1은 ERA5 재분석 자료 및 KIM 모델 자료로부터 탐지된 동아시아 AR의 예시이다. Figures 1a-d는 2020년 6월 1일 0000 UTC 로부터 1일, 3일, 5일, 7일 후에 해당하는 재분석 자료의 AR을 보여주며 Figs. 1e-h는 동일한 날짜를 초기장으로 한 예측기간 1일, 3일, 5일, 7일의 KIM 모델의 예측장을 보여준다. AR은 재분석 자료 및 KIM 모델에서 모두 북서태평양 고기압의 가장자리를 따라 길게 늘어져 나타난다. 이는 KIM 모델이 해당 날짜를 초기장으로 한 예측기간 1일에서 5일까지는 AR 발생을 정성적으로 잘 모의하였음을 보여준다. 그러나 두 자료에서 탐지된 AR의 면적이 다르게 나타나는데 전반적으로 KIM에서 AR이 더 크게 탐지된 것을 확인할 수 있다. 이는 KIM 모델에서 동중국 지역과 일본 남쪽 해상의 IVTA를 더 크게 모의하며 해당 지역까지 포함한 더 넓은 범위가 AR로 탐지되었기 때문이다. 단일 사례에 대한 예시를 통해 KIM의 AR 모의를 확인해보았고 분석기간에 대한 평균적인 모의 능력을 확인해보고자 한다.
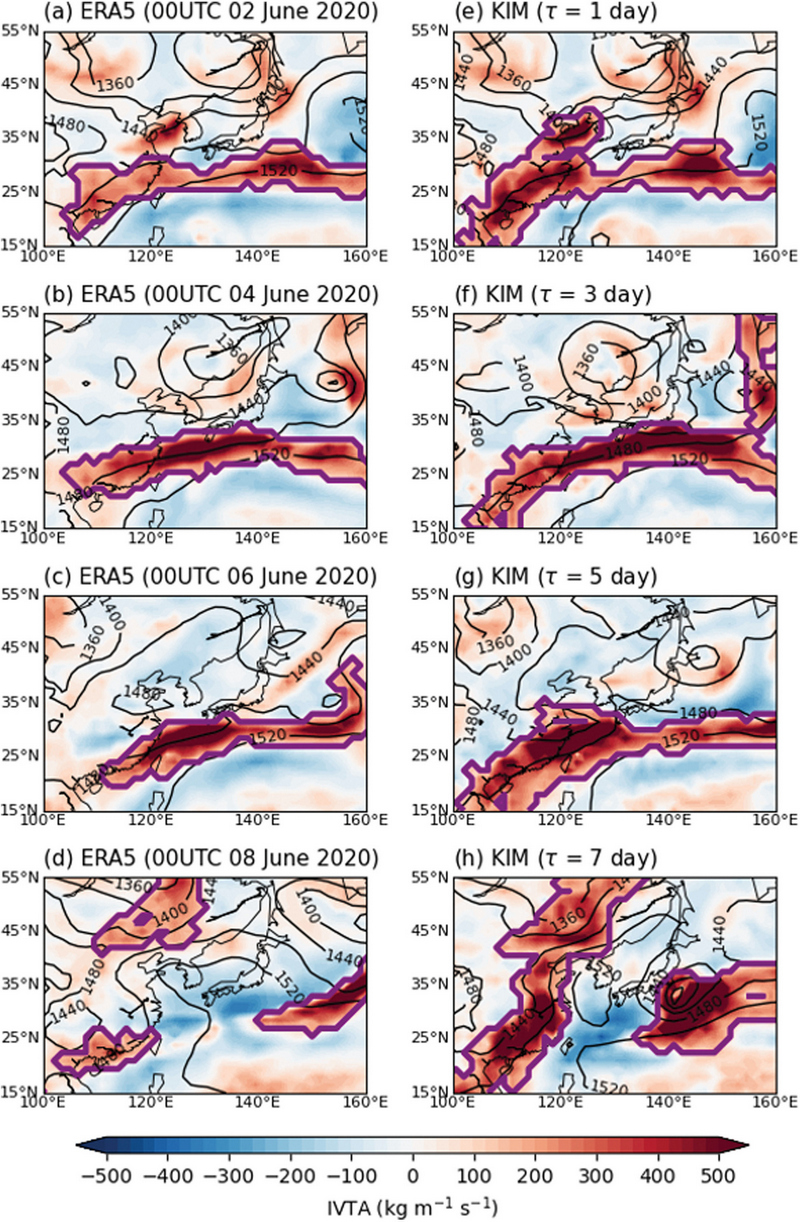
Spatial distribution of 850 hPa geopotential height (gpm, black contoured), IVTA (kg m-1 s-1, shaded) and ARs (purple contoured) for every 2 days from 0000 UTC June 02, 2020 to 0000 UTC June 08, 2020 from (a-d) ERA5. (e-h) Same as in (a-d) but from KIM forecast at each lead time, initialized at 0000 UTC June 01, 2020.
Figure 2는 재분석자료와 KIM 모델에서의 2020~2022년 여름철(6~8월) 초기장으로부터 1일, 3일, 5일, 7일 예측장에서 AR 빈도수를 보여준다. AR 빈도수는 각 격자점에서 전체 기간 중 AR이 탐지된 기간의 비율로 계산하였다. 재분석장에서 AR은 예측기간 1일부터 예측기간 7일까지 동중국 내륙부터 한국을 거쳐 북서태평양까지 동서 방향으로 길게 약 20% 이상의 빈도를 보이고, 일본 동쪽 북서태평양 공해에서 최대 30% 이상의 빈도를 갖는다. 이는 동아시아의 여름철 AR이 북서태평양 고기압의 가장자리를 따라 빈번하게 나타난다는 선행연구와 일치하는 결과이다(Kamae et al., 2017; Park et al., 2021; Kwon et al., 2022; Kim et al., 2023).
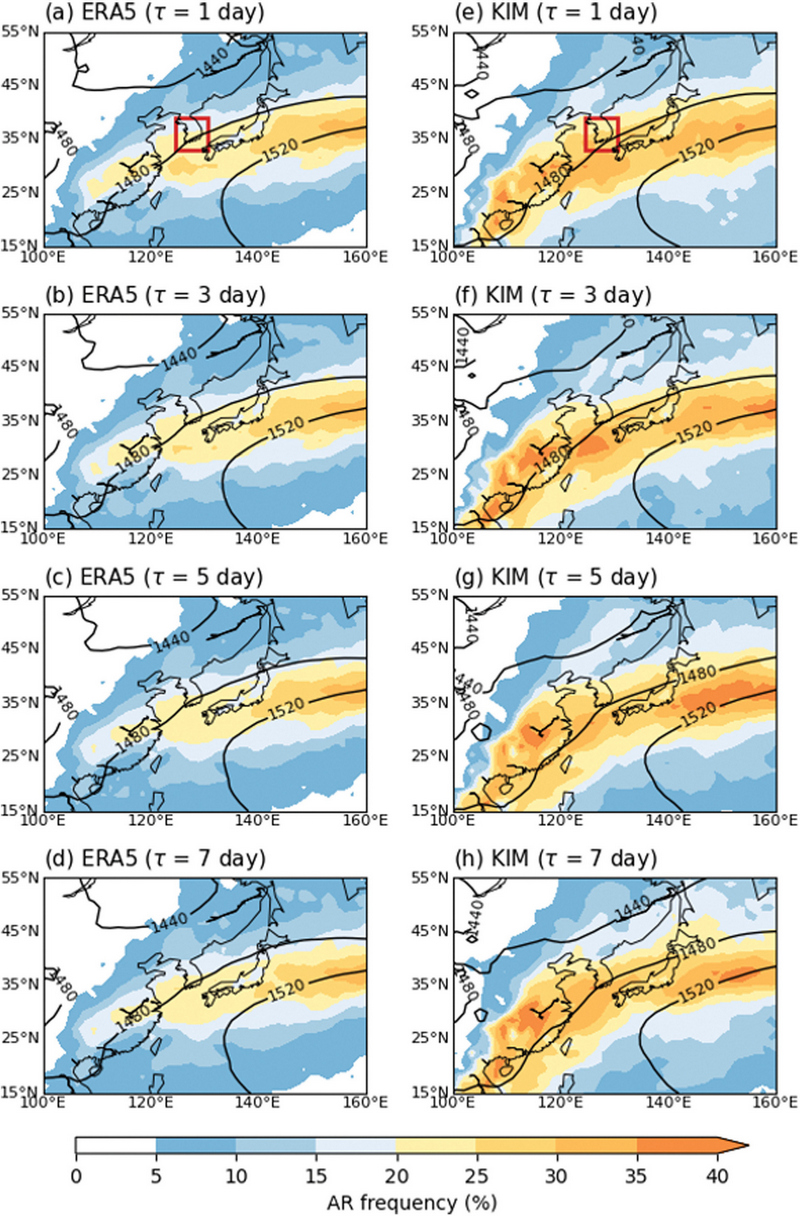
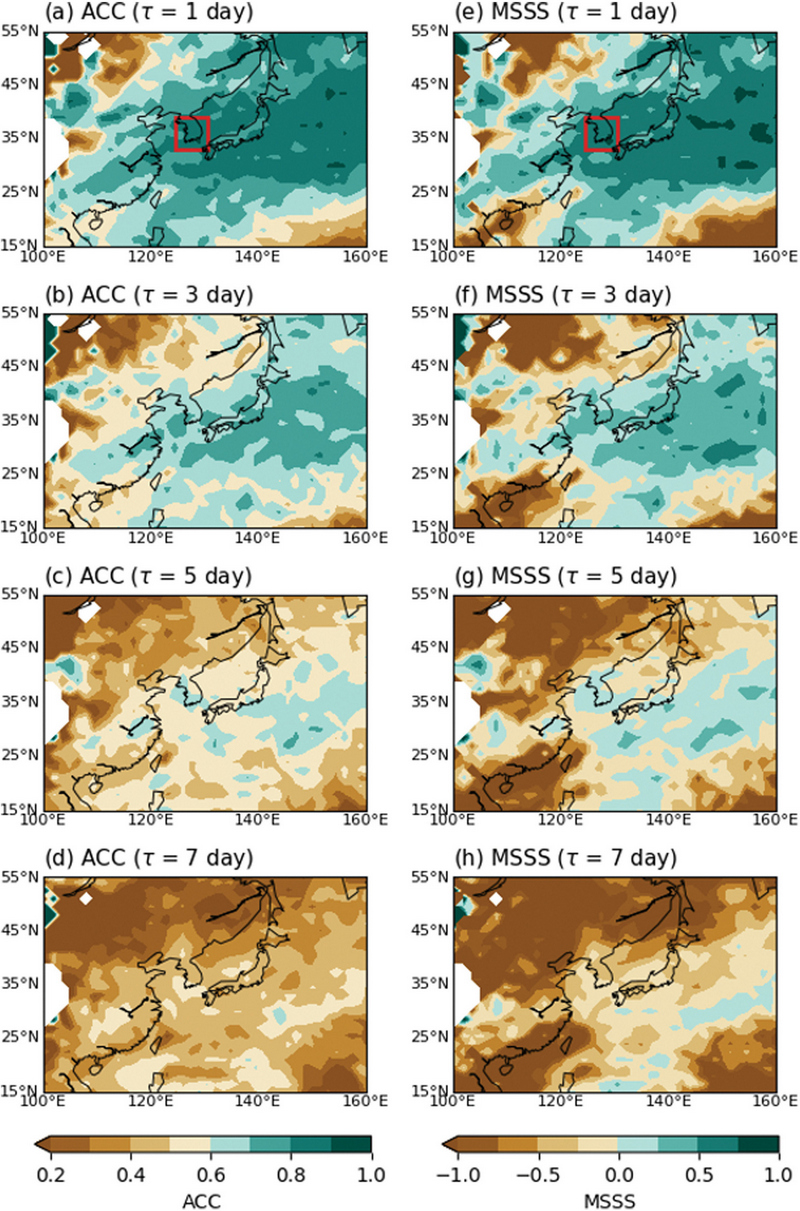
Summer (JJA) climatology of the AR frequency (%, shaded) and 850 hPa geopotential height (gpm, black contoured) from (a-d) ERA5 and (e-h) KIM during 2020~2022. The forecast lead time τ is method to KIM forecasts. The red box indicates the region of South Korea (124.5o~130.5oE, 33o~39oN).
KIM 모델에서 분석 기간 3년 동안 여름철 평균 AR은 관측과 유사하게 남동중국부터 한반도와 일본 지역까지 북서태평양 고기압의 가장자리를 따라 빈번하게 발생한다. 그러나 KIM 모델은 이 기간의 AR 빈도수를 최대 40%까지로 모의하며 전반적으로 ERA5 재분석자료보다 높은 AR 빈도수를 보인다. 이렇듯 KIM 모델은 정성적으로 AR 발생의 분포를 잘 모의 하지만 정량적으로는 AR 빈도수를 과대모의한다.
KIM 모델과 재분석자료간의 AR 빈도수의 편차와 평균 제곱근 오차(Root-Mean Squared Error, 이하 RMSE)를 이용하여 AR 빈도수의 과대모의 경향을 정량적으로 평가하였다. Figures 3a-d는 KIM 모델과 ERA5 재분석자료간의 AR 빈도수 편차를 나타낸다. 예측기간 1일차에는 남동중국 지역을 제외하고는 편차가 약 10% 이하로 나타나며(Fig. 3a), 예측기간이 길어짐에 따라 점차 편차가 커진다(Figs. 3b-d). Figures 3e-h는 모델과 관측값 사이의 RMSE를 예측기간별로 나타낸다. RMSE의 분포는 Figs. 3a-d에서의 모델과 관측의 예측기간별 AR 발생빈도 편차와 유사한 분포를 보인다. RMSE 값은 예측 시작 약 3일부터 남동중국 지역을 중심으로 약 45% 이상으로 크게 나타나며 예측기간 약 5일부터는 한반도와 일본 지역에서도 약 45% 이상으로 점차 큰 값을 보인다. 이를 통해 KIM 모델은 전반적으로 여름철 동아시아 지역 AR빈도수를 과대모의하는 경향이 있으며, 예측기간이 길어짐에 따라 점차 넓은 지역에서 과대모의의 정도가 커지는 것을 확인할 수 있다.
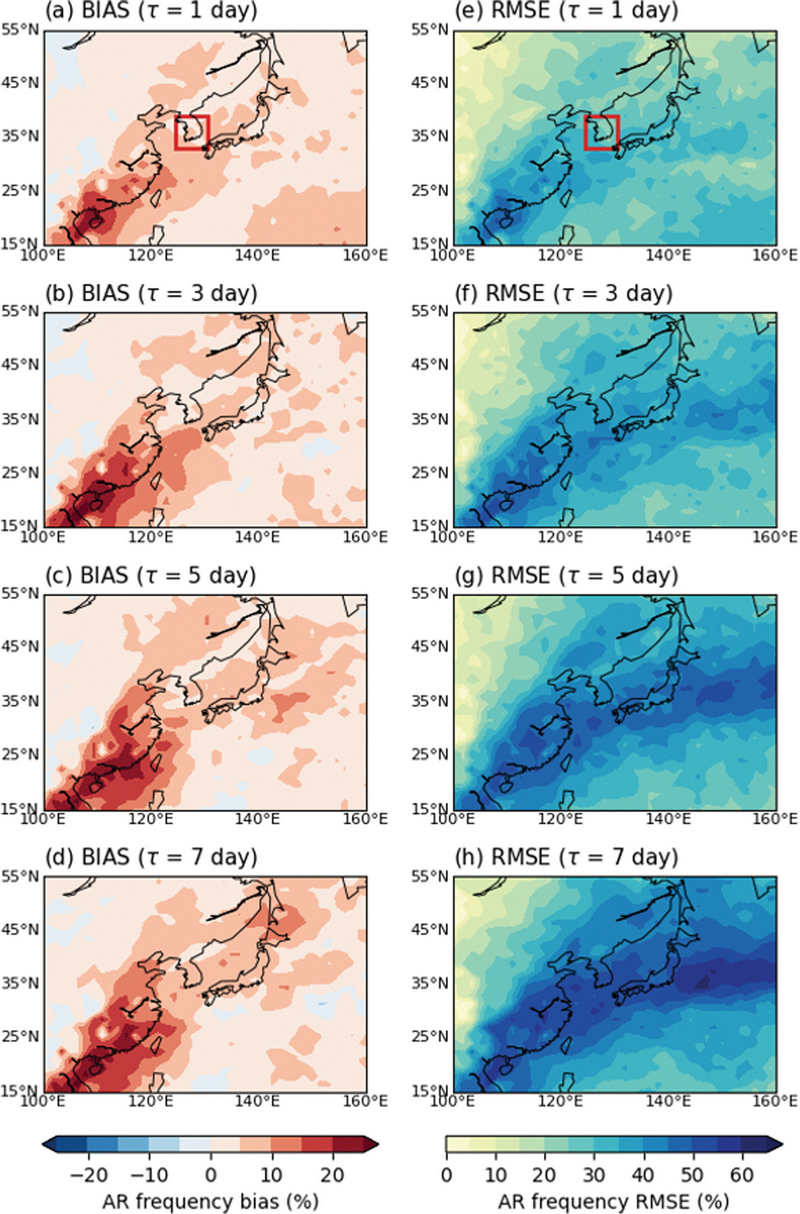
(a-d) Biases (KIM minus ERA5) and (e-h) RMSE of the AR frequency during 2020~2022 at each lead time.
한반도 지역을 중심으로 AR의 빈도수와 편차 그리고 평균 제곱근 오차를 추가적으로 확인해보았다. Figure 4a는 예측기간 0일에서 11일까지의 AR 빈도수 및 편차를 한반도 지역(124.5o~130.5oE, 33o~39oN)에서 영역 평균하여 나타낸 것이다. 한반도 지역 AR빈도수는 재분석자료에서 약 20%, KIM 모델에서 약 22%로 모델이 초기장에서부터 AR 빈도수를 과대모의한다. 모델에서의 과대모의 경향은 예측기간이 길어질수록 뚜렷하게 나타나는데 모델과 재분석장의 발생빈도 편차는 약 2%에서 시작하여 예측기간 11일에 11%까지 증가한다. Figure 4b는 한반도 지역에서 영역 평균된 AR 빈도수의 RMSE를 나타냈다. 모델의 편차와 마찬가지로 RMSE도 예측기간이 길어짐에 따라 값이 커지는 경향을 보였다. RMSE는 예측기간 0일차에서 약 23%의 값을 보이며 예측기간이 길어짐에 따라 지속적으로 증가한다. 예측기간 9일차에는 57%의 값을 보이고, 그 이후에는 그 값이 유지된다.
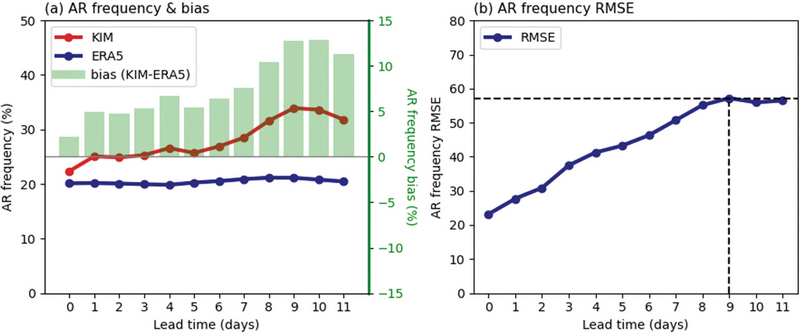
(a) Climatology (red for KIM and blue for ERA5) and model biases (green bars) of the AR frequency averaged over the South Korea (see the box in Fig. 2a) at each lead time. (b) The RMSE of the AR frequency averaged over the South Korea at each lead time. The black dashed lines indicate the lead time when RMSE is saturated.
3.2 KIM 모델의 AR 예측성 검정
KIM 모델에서의 AR 예측성을 정량적으로 확인해 보기 위해 예측성 평가 인자를 사용해 검정했다. Figure 5는 2020~2022년 여름철(6~8월) 초기장으로부터 예측기간에 따른 ACC와 MSSS를 나타낸다. 초기 예측장의 ACC는 동아시아 지역에서 전반적으로 0.6 이상의 값을 보이며(Fig 5a), 이는 예측기간 3일까지 지속된다(Fig 5b). ACC 값은 예측기간이 길어지면서 지속적으로 감소하며, 예측기간 약 5일부터 0.6 이하로 나타난다. 한반도와 일본은 다른 지역에 비해 보다 더 긴 예측 기간 동안 높은 ACC 값을 가지며 다른 동아시아 지역보다 비교적 높은 예측성을 보인다. Figures 5e-h은 예측기간에 따른 MSSS를 나타냈다. 초기 예측장부터 예측기간 3~4일까지 전반적으로 모든 동아시아 지역에서 0 이상의 MSSS 값이 나타난다. 이러한 MSSS 값은 예측기간이 길어짐에 따라 점차 감소하다가, 예측기간 5일차부터 점차 음수의 값을 보인다. 한반도 및 일본 남부 지역에서는 비교적 긴 예측기간까지 0 이상의 MSSS 값이 나타났고, 이는 ACC의 결과와 함께 한반도 및 일본 남부 지역에서의 AR예측성이 다른 동아시아 지역보다 높음을 보여준다.
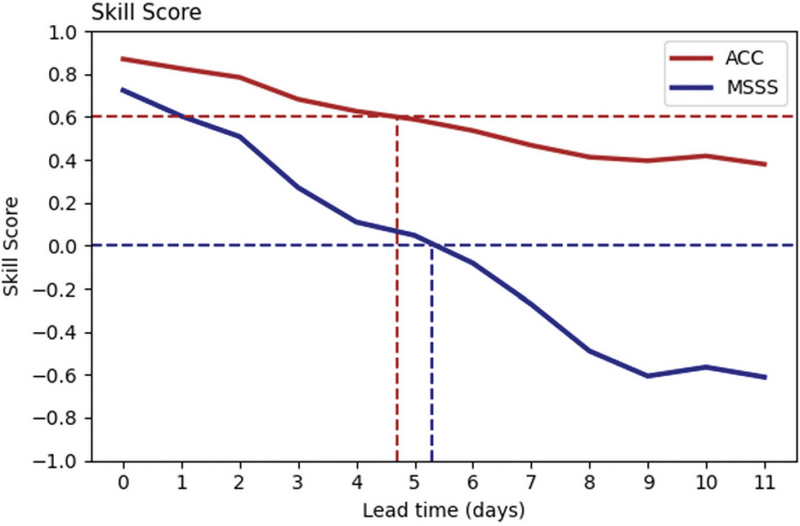
Figure 6은 한반도 지역(124.5o~130.5oE, 33o~39oN)에서 영역 평균된 ACC와 MSSS의 값을 나타낸다. 예측기간이 길어짐에 따라 ACC와 MSSS가 선형적으로 감소함을 보여준다. ACC는 예측기간 5일에서 약 0.6의 값을 보이며, MSSS도 예측기간 5일에서 약 0의 값을 보인다. 두 개의 예측성 지표를 고려해 보았을 때, 한반도 지역의 AR 발생빈도의 예측성은 약 5일정도로 나타난다.
3.3 KIM 모델의 AR 예측 오차 원인
AR 발생빈도 오차의 원인을 파악하기 위해 동아시아 AR 발생빈도의 예측성이 약 5일인 점을 고려하여 예측기간 5일에서 수증기 수지 분석을 수행했다. AR은 IVT를 이용하여 탐지하기에 IVT의 오차 분석을 통해서 AR 발생빈도의 오차의 원인을 파악하고자 하였다. 본 연구에서는 IVT의 오차를 3개의 항으로 나누어 살펴보았다. Figure 7은 예측기간 5일에서 IVT의 오차를 나타내며, Fig. 7a는 모델의 비습 오차(q'Vobs)에 의한 IVT 오차, Fig. 7b는 모델의 수평 바람 오차(qobsV')에 의한 IVT 오차, 그리고 Fig. 7c는 IVT 오차의 비선형성분(q'V')을 나타낸다. IVT의 오차는 동중국해와 북서태평양 고기압의 가장자리를 중심으로 크게 나타난다. 예측기간 5일에서 모델의 비습 오차(q'Vobs)에 의한 IVT 오차와 I VT 오차의 비선형성분(q'V')은 모두 약 100 kg m-1 s-1의 값을 보이며, 유사한 크기를 가진다. 이에 비해 모델의 수평 바람 오차(qobsV')에 의한 IVT 오차는 약 400 kg m-1 s-1까지의 값을 가지며 앞서 살펴본 두 I VT 오차 성분에 비해 상대적으로 큰 값을 가진다. 즉 모델의 I VT 오차는 수평 바람 오차에 의해 가장 크게 나타난다. 실제로 모델과 관측에서의 850 hPa 지위고도와 북서태평양 고기압 가장자리를 살펴보았을 때 예측기간이 길어짐에 따라 북서태평양 고기압 가장자리 위치오차가 증가함을 확인하였다(Fig. 8). 이를 종합해 볼 때, 지위고도에 의한 오차 개선이 모델의 IVT 및 AR 발생빈도의 오차 개선에 있어서 중요함을 알 수 있다.
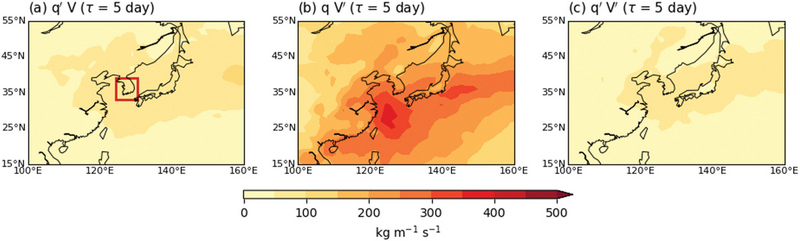
Decomposition of IVT biases from KIM at 5-day forecast. (a) IVT biases by moisture. (b) IVT biases by wind biases. (c) IVT biases by nonlinear interactions of moisture and wind biases.
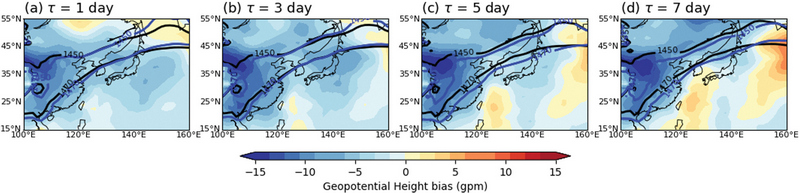
850 hPa geopotential height (gpm, black contoured) from ERA5 (gpm, black contoured), KIM (gpm, blue contoured) and geopotential height bias (gpm, shaded) during 2020~2022.
Figure 9은 한반도 지역에서 평균된 모델의 IVT 오차 성분의 상대적 중요성을 보여준다. 한반도 지역에서의 IVT 오차는 수평 바람 오차에 의한 값(qobsV')이 가장 크게 나타나고 예측기간에 따른 오차의 증가 정도도 가장 크게 나타난다. 비습 오차(q'Vobs)와 오차의 비선형항(q'V')은 비슷한 값의 범위를 보인다. 따라서 한반도 지역에서의 수증기 수송 오차는 순환장에 의한 오차가 가장 크게 기여하며 순환장에 의한 오차의 개선이 이루어진다면 향후 한반도 및 동아시아 AR발생빈도의 예측성을 높이는 데에 기여할 수 있을 것이다.
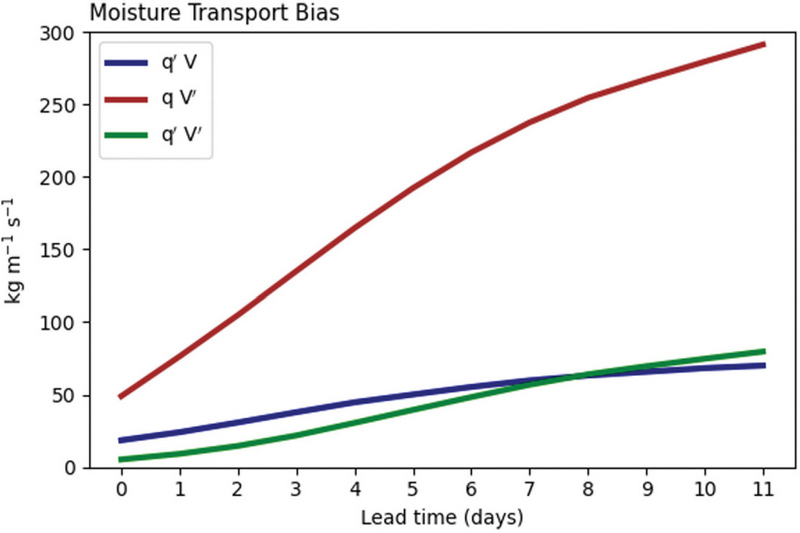
Decomposition of IVT biases from KIM over South Korea. The blue, red, and green indicate the IVT biases by moisture, those by wind biases, and those by nonlinear interactions of moisture and wind biases, respectively.
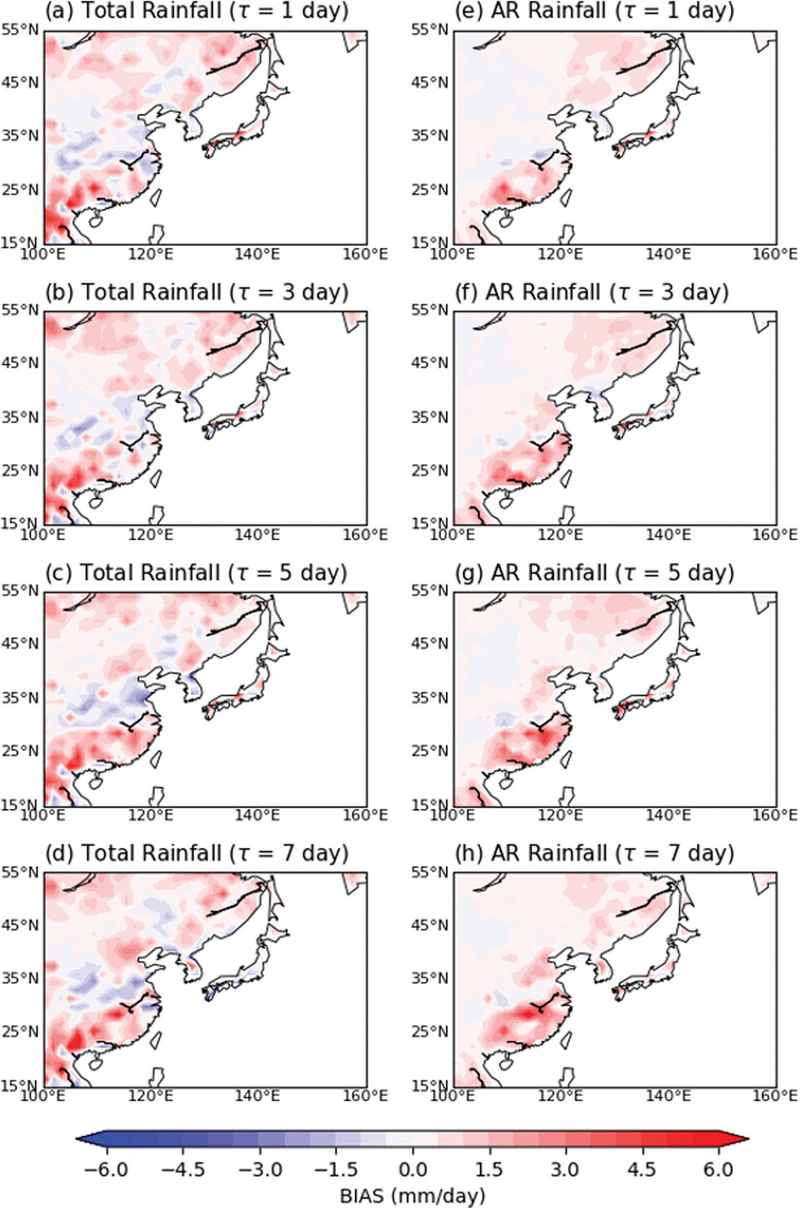
Figures 10a-d는 여름철 총 강수량에 대한 모델과 관측간의 편차를, Figs. 10e-h는 AR의 영향을 받은 강수량(AR rainfall, 이하 AR 강수)에 대한 모델과 관측간의 편차를 나타낸다. AR의 영향을 받은 강수는 AR이 존재할 때의 강수로 정의하였으며, 격자화된 강수자료에서 AR과 강수가 겹치는 지점의 강수만을 고려하였다(Moon et al., 2019). 관측으로는 Climate Prediction Center (CPC; Xie et al., 2007)에서 제공하는 강수 자료를 사용하였으며 이를 KIM 모델에서 제공하는 강수 자료와 비교하였다. KIM 모델은 한반도에서의 총 강수량을 전반적으로 과소모의하지만 남동중국 일부 지역에서 과대모의를 보이며, AR 강수의 경우 모델에서 전반적으로 과대모의가 나타나고 특히 남동중국 지역에서 그 정도가 크게 나타난다(Figs. 10e-h). AR 강수가 총 강수량의 일부임을 고려하였을 때, 모델이 남동중국 지역에서 총 강수량을 과대모의하는 것은 AR의 과대모의로 일부 설명 가능할 것으로 보인다. 따라서 AR의 예측성 개선이 이루어진다면 강수의 예측성 또한 개선될 것이다.
4. 요약 및 토의
본 연구에서는 한국형수치예보모델 KIM을 이용하여 2020~2022년 여름철 AR 예측성을 검증하였다. ERA5 재분석자료를 관측으로 하여 초기화 날부터 예측기간 11일까지의 AR 발생을 비교해본 결과, KIM모델은 북서태평양 고기압의 가장자리를 따라 빈번하게 발생하는 AR 분포를 정성적으로 잘 예측하였으나 빈도수를 과대모의하였다. 모델과 재분석장의 발생빈도 편차와 평균 제곱근 오차는 초기 남중국 일부 지역에서 크게 나타나며 예측기간이 길어짐에 따라 한반도를 거쳐 일본 지역까지 넓은 범위에서 크게 나타났다. 한반도 지역을 중심으로 살펴본 결과 초기장에서 KIM은 재분석 자료에 비해 AR 빈도수를 약 2%정도 과대모의하며 모델과 재분석장의 발생빈도 편차는 예측기간 11일에 약 11%까지 증가하였다.
KIM 모델에서의 AR 예측성을 정량적으로 확인해 보기 위해 이상상관계수(ACC)와 평균제곱 예측성(MSSS)을 예측성 평가인자로 사용하여 검증하였다. 전반적으로 예측기간 5일 정도에서 ACC는 0.6 이하의 값이, MSSS는 0 이하의 값이 나타나는 것을 알 수 있으며, 이는 KIM 모델에서의 동아시아 여름철 AR 예측성이 5일 정도로 나타남을 의미한다. 한반도지역을 중심으로 살펴본 결과 ACC는 예측기간 5일에서 약 0.6의 값을 보이며, MSSS는 예측기간 6일에서 약 0의 값을 보인다. 이는 한반도에서 KIM의 AR예측성이 약 5일정도로 나타남을 의미한다.
AR 예측성의 한계를 파악하기 위해 IVT를 모델의 비습 오차, 수평 바람 오차, 오차의 비선형항으로 나누어 각 항의 기여를 살펴본 결과 수평 바람 오차에 의한 수증기 수송 오차가 가장 크게 나타났다. AR이 IVT를 이용하여 탐지됨을 고려해볼 때 순환장의 오차 개선이 이루어진다면 향후 동아시아 AR의 예측성을 높이는 데에 기여할 수 있을 것이다.
추가적으로 AR과 강수의 관계를 살펴보기 위해 모델과 재분석장간의 총 강수량과 AR 강수의 편차를 살펴보았다. 총 강수량과 AR 강수 모두 남동중국 지역에서 과대모의가 나타났으며 이는 AR이 과대모의 되는 지역과 일치하였다. 따라서 AR 예측성이 개선된다면 강수의 예측성 또한 개선될 것으로 기대할 수 있다.
KIM 모델은 초기장(lead time day 0)부터 모형 자체가 갖는 일정한 구조적 오차가 존재한다. 분석기간 3년(2020~2022년) 동안 각 예측기간에 따른 모델과 재분석장간의 I VT 평균오차를 계산하여 구조오차를 제거해 보았을 때, 모델의 AR 예측성이 일부 향상되는 것을 확인할 수 있었다. 비록 3년이라는 기간의 한계로 본문에는 그림을 제시하지 않았지만, 이는 장기적분에 따라 발생하는 모델의 구조 오차를 이해하고 이를 예측성 평가에 활용할 필요가 있음을 시사한다.
본 연구에서는 KIM의 모의 성능 검증을 위한 목적으로 단일 알고리즘(Park et al., 2023)을 이용하여 동아시아 여름철 AR의 예측성을 확인하였다. AR 탐지에 사용하는 알고리즘에 따라서도 예측성의 차이가 나타날 수 있다. Nayak et al. (2014)는 IVT와 연직 적분된 수증기(Integrated Water Vapor, IWV)를 이용하여 AR을 탐지하는 서로 다른 알고리즘을 비교했는데, IVT를 이용하여 AR을 탐지하는 알고리즘에서 AR의 예측성이 더 크게 나타남을 보였다. 이외에도 AR 탐지 임계 값과 세부적인 탐지 방법에 따라 AR의 예측성이 다르게 나타날 수 있기에 추후 다양한 알고리즘을 활용하여(Pan and Lu, 2019; Liang and Yong, 2021) 추가적인 분석을 수행할 필요가 있다. 이를 통해 동아시아 AR 예측성을 보다 정량적으로 이해할 수 있을 것이다.
Acknowledgments
이 연구는 기상청 국립기상과학원 「위험기상에 대한 분석·예보의 융합기술 고도화」(KMA2018-00121)와 2023년도 해양수산부 재원으로 해양수산과학기술진흥의 지원을 받아 수행되었습니다(20210427, 과학기술기반 해양환경영향평가 기술개발).
References
-
Baggett, C. F., E. A. Barnes, E. D. Maloney, and B. D. Mundhenk, 2017: Advancing atmospheric river forecasts into subseasonal‐to‐seasonal time scales. Geophys. Res. Lett., 44, 7528-7536.
[https://doi.org/10.1002/2017GL074434]

-
DeFlorio, M. J., D. E. Waliser, B. Guan, F. M. Ralph, and F. Vitart, 2019: Global evaluation of atmospheric river subseasonal prediction skill. Climate Dyn., 52, 3039-3060.
[https://doi.org/10.1007/s00382-018-4309]

-
Dettinger, M. D., F. M. Ralph, T. Das, P. J. Neiman, and D. R. Cayan, 2011: Atmospheric Rivers, Floods and the Water Resources of California. Water, 3, 445-478.
[https://doi.org/10.3390/w3020445]

-
Dhana Laskhmi, D., and A. N. V. Satyanarayana, 2020: Climatology of landfalling atmospheric Rivers and associated heavy precipitation over the Indian coastal regions. Int. J. Climatol., 40, 5616-5633.
[https://doi.org/10.1002/joc.6540]

-
Gimeno, L., and Coauthors, 2016: Major mechanisms of atmospheric moisture transport and their role in extreme precipitation events. Annu. Rev. Environ. Resour., 41, 117-141.
[https://doi.org/10.1146/annurev-environ-110615-085558]

-
Guan, B., and D. E. Waliser, 2015: Detection of atmospheric rivers: evaluation and application of an algorithm for global studies. J. Geophys. Res. Atmos., 120, 12514-12535.
[https://doi.org/10.1002/2015JD024257]

-
Hwang, J., H.-O. Cho, Y. Lim, S.-W. Son, E.-J. Kim, J.-O. Lim, and K.-O. Boo, 2020: Extratropical prediction skill of KMA GDAPS in January 2019. Atmosphere, 30, 115-124. (in Korean with English abstract)
[https://doi.org/10.14191/Atmos.2020.30.2.115]

-
Hersbach, H., and Coauthors, 2020: The ERA5 global reanalysis. Quart. J. Roy. Meteor. Soc., 146, 1999-2049.
[https://doi.org/10.1002/qj.3803]

-
Hong, S.-Y., and Coauthors, 2013: The Global/Regional Integrated Model system (GRIMs). Asia-Pac. J. Atmos. Sci., 49, 219-243.
[https://doi.org/10.1007/s13143-013-0023-0]

-
Hong, S.-Y., and Coauthors, 2018: The Korean Integrated Model (KIM) system for global weather forecasting. Asia-Pac. J. Atmos. Sci., 54, 267-292.
[https://doi.org/10.1007/s13143-018-0028-9]

-
Kataoka, T., H. Tatebe, H. Koyama, T. Mochizuki, K. Ogochi, H. Naoe, Y. Imada, H. Shiogama, M. Kimoto, and M. Watanabe, 2020: Seasonal to decadal predictions with MIROC6: Description and basic evaluation. J. Adv. Modeling Earth Syst., 12, e2019MS002035.
[https://doi.org/10.1029/2019MS002035]

-
Kamae, Y., W. Mei, S.-P. Xie, M. Naoi, and H. Ueda, 2017a: Atmospheric rivers over the Northwestern Pacific: Climatology and interannual variability. J. Climate, 30, 5605-5619.
[https://doi.org/10.1175/JCLI-D-16-0875.1]

-
Kamae, Y., W. Mei, and S.-P. Xie, 2017b: Climatological relationship between warm season atmospheric rivers and heavy rainfall over East Asia. J. Meteor. Soc. Japan Ser. II, 95, 411-431.
[https://doi.org/10.2151/jmsj.2017-027]

-
Kim, G., S.-Y. Back, Y. Kwon, and S.-W. Son, 2023: Comparison of atmospheric river detection algorithms in East Asia, Atmosphere, 33, 399-411. (in Korean with English abstract)
[https://doi.org/10.14191/Atmos.2023.33.4.399]

-
Kim, J., H. Moon, B. Guan, D. E. Waliser, J. Choi, T. Y. Gu, and Y.-H. Byun, 2021: Precipitation characteristics related to atmospheric rivers in East Asia. Int. J. Climatol., 41, E2244-E2257.
[https://doi.org/10.1002/joc.6843]

-
Kim, S.-W., H. Kim, K. Song, S.-W. Son, Y. Lim, H.-S. Kang, and Y.-K. Hyun, 2018: Subseasonal-to-Seasonal (S2S) prediction skills of GloSea5 model: Part 1. Geopotential height in the Northern Hemisphere extratropics. Atmosphere, 28, 233-245.
[https://doi.org/10.14191/Atmos.2018.28.3.233]

-
Kwon, Y., C. Park, S.-Y. Back, S.-W. Son, J. Kim, and E. J. Cha, 2022: Influence of atmospheric rivers on regional precipitation in South Korea, Atmosphere, 32, 135-148. (in Korean with English abstract)
[https://doi.org/10.14191/atmos.2022.32.2.135]

-
Lavers, D. A., R. P. Allan, E. F. Wood, G. Villarini, D. J. Brayshaw, and A. J. Wade, 2011: Winter floods in Britain are connected to atmospheric rivers. Geophys. Res. Lett., 38, L23803.
[https://doi.org/10.1029/2011GL049783]

-
Lavers, D. A., and G. Villarini, 2013: The nexus between atmospheric rivers and extreme precipitation across Europe. Geophys. Res. Lett., 40, 3259-3264.
[https://doi.org/10.1002/grl.50636]

-
Lavers, D. A., and G. Villarini, 2015: The contribution of atmospheric rivers to precipitation in Europe and the United States. J. Hydrol., 522, 382-390.
[https://doi.org/10.1016/j.jhydrol.2014.12.010]

-
Liang, J., and Y. Yong, 2021: Climatology of atmospheric rivers in the Asian monsoon region. Int. J. Climatol., 41, E810-E818.
[https://doi.org/10.1002/joc.6729]

-
Liu, B., J. Su, L. Ma, Y. Tang, X. Rong, J. Li, H. Chen, B. Liu, L. Hua, and R. Wu, 2021: Seasonal prediction skills in the CAMS-CSM climate forecast system. Climate Dyn., 57, 2953-2970.
[https://doi.org/10.1007/s00382-021-05848-z]

-
Moon, H., J. Kim, B. Guan, D. E. Waliser, J. Choi, T.-Y. Goo, Y. Kim, and Y.-H. Byun, 2019: The effects of atmospheric river landfalls on precipitation and temperature in Korea. Atmosphere, 29, 343-353. (in Korean with English abstract)
[https://doi.org/10.14191/ATMOS.2019.29.4.343]

-
Mundhenk, B. D., E. A. Barnes, and E. D. Maloney, 2016: All-season climatology and variability of atmospheric rivers over the North Pacific. J. Climate, 29, 4885-4903.
[https://doi.org/10.1175/JCLI-D-15-0655.1]

-
Mundhenk, B. D., E. A. Barnes, E. D. Maloney, and C. F. Baggett, 2018: Skillful empirical subseasonal prediction of landfalling atmospheric river activity using the Madden-Julian oscillation and quasi-biennial oscillation. Npj Climate Atmos. Sci., 1, 20177.
[https://doi.org/10.1038/s41612-017-0008-2]

-
Nash, D., D. E. Waliser, B. Guan, H. Ye, and F. M. Ralph, 2018: The role of atmospheric rivers in extratropical and polar hydroclimate. J. Geophys. Res. Atmos., 123, 6804-6821.
[https://doi.org/10.1029/2017JD028130]

-
Nayak, M. A., G. Villarini, and D. A. Lavers, 2014: On the skill of numerical weather prediction models to forecast atmospheric rivers over the central United States. Geophys. Res. Lett., 41, 4354-4362.
[https://doi.org/10.1002/2014GL060299]

-
Nayak, M. A., and G. Villarini, 2017: A long-term perspective of the hydroclimatological impacts of atmospheric rivers over the central United States. Water Resour. Res., 53, 1144-1166.
[https://doi.org/10.1002/2016WR019033]

-
Newell, R. E., N. E. Newell, Y. Zhu, and C. Scott, 1992: Tropospheric rivers?—A pilot study. Geophys. Res. Lett., 19, 2401-2404.
[https://doi.org/10.1029/92GL02916]

-
Pan, M., and M. Lu, 2019: A novel atmospheric river identification algorithm. Water Resour. Res, 55, 6069-6087.
[https://doi.org/10.1029/2018WR024407]

-
Pan, M., and M. Lu, 2020: East Asia atmospheric river catalog: Annual cycle, transition mechanism, and precipitation. Geophys. Res. Lett., 47, e2020GL089477.
[https://doi.org/10.1029/2020GL089477]

-
Park, C., S.-W. Son, and H. Kim, 2021: Distinct features of atmospheric rivers in the early versus late East Asian summer monsoon and their impacts on monsoon rainfall. J. Geophys. Res. Atmos., 126, e2020JD033537.
[https://doi.org/10.1029/2020JD033537]

-
Paltan, H., D. Waliser, W. H. Lim, B. Guan, D. Yamazaki, R. Pant, and S. Dadson, 2017: Global floods and water availability driven by atmospheric rivers. Geophys. Res. Lett., 44, 10387-10395.
[https://doi.org/10.1002/2017GL074882]

-
Ralph, F. M., P. J. Neiman, G. A. Wick, S. I. Gutman, M. D. Dettinger, D. R. Cayan, and A. B. White, 2006: Flooding on California’s Russian River: role of atmospheric rivers. Geophys. Res. Lett., 33, L13801.
[https://doi.org/10.1029/2006GL026689]

-
Ralph, F. M., and M. D. Dettinger, 2012: Historical and national perspectives on extreme west coast precipitation associated with atmospheric Rivers during December 2010. Bull. Amer. Meteor. Soc ., 93, 783-790.
[https://doi.org/10.1175/BAMS-D-11-00188.1]

-
Shu, J., A. Y. Shamseldin, and E. Weller, 2021: The impact of atmospheric rivers on rainfall in New Zealand. Sci. Rep., 11, 1-11.
[https://doi.org/10.1038/s41598-021-85297-0]

-
Son, S.-W., H. Kim, K. Song, S.-W. Kim, P. Martineau, Y.-K. Hyun, and Y. Kim, 2020: Extratropical prediction skill of the subseasonal-to-seasonal (S2S) prediction models. J. Geophys. Res. Atmos., 125, e2019-JD031273.
[https://doi.org/10.1029/2019JD031273]

-
Song, K., H. Kim, S.-W. Son, S.-W. Kim, H.-S. Kang, and Y.-K. Hyun, 2018: Subseasonal-to-Seasonal (S2S) prediction of GloSea5 Model: Part 2. Stratospheric sudden warming. Atmosphere, 28, 123-139. (in Korean with English abstract)
[https://doi.org/10.14191/Atmos.2018.28.2.123]

-
Tian, Y., Y. Zhao, J. Li, B. Chen, L. Deng, and D. Wen, 2024: East Asia atmospheric river forecast with a deep learning method: GAN-UNet. J. Geophys. Res. Atmos., 129, e2023JD039311.
[https://doi.org/10.1029/2023JD039311]

-
Wick, G. A., P. J. Neiman, F. M. Ralph, and T. M. Hamill, 2013: Evaluation of forecasts of the water vapor signature of atmospheric rivers in operational numerical weather prediction models. Weather Forecast, 28, 1337-1352.
[https://doi.org/10.1175/WAF-D-13-00025.1]

-
Xie, P., M. Chen, S. Yang, A. Yatagai, T. Hayasaka, Y. Fukushima, and C. Liu, 2007: A gauge- based analysis of daily precipitation over East Asia. J. Hydrometeorol., 8, 607-626.
[https://doi.org/10.1175/JHM583.1]

-
Zhu, Y., and R. E. Newell, 1994: Atmospheric rivers and bombs. Geophys. Res. Lett., 21, 1999-2002.
[https://doi.org/10.1029/94GL01710]

-
Zhu, Y., and R. E. Newell, 1998: A proposed algorithm for moisture fluxes from atmospheric rivers. Mon. Wea. Rev., 126, 725-735.
[https://doi.org/10.1175/1520-0493(1998)126<0725:APAFMF>2.0.CO;2]