한반도 겨울철 강수 유형에 따른 전지구 수치모델(GRIMs) 예측성능 검증

1. 서 론

수치예보모델의 각종 예측성능 검증 결과에 대한 구체적인 해석은 대기과학 분야의 수치모델링 연구 및 현업예보에 있어서 매우 중요한 정보이다. 따라서, 수치예보모델에 대한 예측성능 검증 방법을 적절하게 선택하고 이를 어떻게 설계하느냐에 따라서 수치예보모델 개발자, 예보관, 나아가 수치예보모델의 예측 산출물을 활용하는 다양한 분야의 사용자에게 유용한 정보를 줄 수 있다(Casati et al., 2008). 수치예보모델 결과에서 활용되는 가장 중요한 기상요소 중의 하나는 강수이다. 일상생활 뿐만 아니라 각종 산업, 농업, 방재 등 많은 분야에서 상당한 수준의 정확한 강수예보 산출물이 요구되기 때문에 현업기관에서는 이미 강수의 정량예보를 수행한지 오래되었고, 산출된 강수예보에 대한 예측 정확도를 평가함으로써 산출자료를 적절히 활용하기 위한 노력을 기울이고 있다(Olson et al., 1995; Ebert et al., 2003).

수치예보모델에서 생산된 특정 사례의 강수예보 산출물뿐만 아니라, 일정기간에 대한 통계적 강수 검증 결과도 예보관이 현장에서 최종 결정을 내리는데 유용하게 활용될 수 있음을 경험적으로 알 수 있다. 특히 여러 종류의 전구 및 지역모델들에서 산출된 강수예측 정보를 비교하고 최종 예보를 결정하는 상황에서는 수치예보모델의 강수 예측 경향 및 정확도에 대한 정보는 매우 유용할 것이다. 또한 호우나 대설 등의 악기상 발생이 예상되어 적절한 예보 및 경보가 필요한 경우, 현업에 사용되는 수치예보모델의 강수 예측 정확도에 대한 객관적인 검증 결과가 누적, 확보되어 있다면 이를 통해 예보 결정 근거를 제시할 수 있을 것이다. 따라서, 수치예보모델의 예보 정확도 제고는 자연재해로부터 피해를 경감시키고 기상상황에 민감한 산업분야의 생산성을 높이는데 매우 중요한 밑바탕이 될 것이다(Park, 2013).

수치예보모델의 강수 예측성능은 지속적으로 개선되어 왔으나, 여전히 다른 기상 요소에 비해서도 예측 정확도가 낮으며 큰 오차가 발생할 수 있는 가장 민감한 영역이다(Sanders, 1986; Fritsch et al., 1998; Chang, 2021). 강수 예측 성능은 수치예보모델의 초기조건, 역학 및 물리과정 전반과 연관된 종관시스템 예측에 좌우될 뿐만 아니라 미세물리 및 대류과정과 같은 강수 물리과정, 경계층 및 지표근처의 하층 물리과정 등 개별 물리과정에도 매우 민감하며(Gallus and Bresch, 2006), 지면 피복 및 지형 자료에 의해서도 영향을 받는다(Sud et al., 1988). 따라서, 강수 예측성능이 수치예보모델의 성능을 대표할 수 있다고 해도 과언이 아니며 강수 예측에서의 계통적 오차가 확인된다면 이와 관련된 제반 과정들의 오차 관련성을 규명함으로써 모델 개선 근거로 활용할 수도 있을 것이다.

본 연구에서 수치예보모델의 한반도 강수 예측 정확도를 평가함에 있어 일반적인 강수 전반을 대상으로 하지 않고 강수발생일을 강수 발생 원인과 유형에 따라 분류하고 그룹화하여 그룹별 검증을 시도하였다. 강수를 정확히 예보하기 위해서는 강수현상에 대한 이해가 선행되어야 함은 널리 인식되어 왔고, 이를 위해 강수 발생 기작에 근거하여 강수를 분류하는 많은 선행 연구 결과(Cheong et al., 2006)는 수치예보모델을 개선하기 위한 근거 사례로 활용되어 왔다(Lim and Hong, 2007). 이에 강수의 발생 기작에 따른 수치예보모델의 강수 예측 정확도를 평가해 봄으로써 예보관에게는 수치예보모델 결과를 활용하는데 필요한 참고정보를 제공하고, 연구자들에게는 물리과정 등 수치예보모델의 개선에 기초자료를 제시하고자 하였다. 본 연구에서는 종관규모 기압계의 영향이 우세하고 강수 발생 기작을 분류하기 용이한 겨울철 강수를 검증대상으로 선정하였다. 또한 수치예보모델의 강수 예측성능 평가 및 관련 사례연구가 상당 부분 여름철 악기상에 집중되어 있는 점도 고려하였다.

이 연구에서 강수 예측성능 검증을 수행할 전지구수치예보모델은 GRIMs (Global/Regional Integrated Model system)로 선정하였으며, 2013년 12월~2014년 2월(December-January-February, DJF)에 대하여 단기(3일) 예측 강수검증을 수행하였다. 또한 한반도에서 발생하는 겨울철 강수의 발생 원인을 이론적으로 우선 검토하고, 대상 기간의 강수발생일 전체에 대한 종관분석 및 검토 작업을 통해 이론적 강수 발생 원인에 따라 분류, 그룹화하였다. 이렇게 분류된 강수 유형별 그룹에 대하여 객관적인 강수검증지수를 이용한 분석을 수행하였다.

2. 자료 및 연구방법

2.1 강수 예측성능 검증 방법

한반도 겨울철 강수에 대한 GRIMs의 예측성능을 평가하기 위하여 2013/2014 DJF 기간에 일일 누적강수량 0.1 mm 이상이 기록된 날을 모두 강수발생일로 선별하고 강수 발생 기작에 따른 유형 분류의 대상으로 활용하였다. 선별된 강수발생일을 대상으로 지상 및 상층일기도를 분석하여 해당일에 우세했던 종관기압계의 기본 패턴을 분류하였다. 각 사례일의 기본 종관기압계 패턴에 대하여 천리안 위성에서 제공되는 동일 시간대 합성영상의 구름 형태를 비교, 분석함으로써 해당일이 어떤 강수 유형에 해당하는지 확정하고 동일한 유형별로 그룹화하였다. 또한 동일 기간에 대한 GRIMs의 3일 예측결과 중 분석장과 12시간 예측결과를 종관기압계 기본 패턴 분류에 사용했던 지상 및 상층일기도와 최종 비교함으로써 그 적합성을 최종적으로 검토하였다. 최종 분류 및 검토를 완료하고 각 강수 발생 기작에 따른 유형을 최종적으로 그룹화(Fig. 1)하여 객관적인 강수 검증지수를 분석하였다.

Fig. 1.

The flow chart of methodology : Evaluation of predictability of a global numerical weather prediction model (GRIMs) for the winter precipitation systems over Korea.

3. 결 과

3.1 2013~2014년 겨울철 강수 유형 분류

Figure 2는 3개월의 연구기간에 대하여 AWS 일별 총강수량을 관측지점 수(617개)로 나눈 평균 일강수량(grey bar)과 GRIMs로 예측한 평균 일강수량(solid line)을 시계열로 표출한 것이다. 2013~2014년 DJF 기간 월별 전체 강수발생일을 대상으로 AWS 일누적강수량 평균과 GRIMs의 24시간 누적 예측강수량의 남한지역 평균을 시계열로 비교하였다. AWS 일누적강수량 평균과 모델의 예측 일누적강수량 간 시간 변동에 따른 위상은 거의 일치되어 보이지만, 전반적으로 모델의 예측강수량이 다소 과대모의되는 경향을 보인다. 여기서 전체 90일 중 일누적강수량 0.1 mm day^–1 이상의 강수가 관측된 72일에 대하여 종관일기도와 위성영상을 분석함으로써 앞에서 정의한 3가지 강수 유형으로 나누어 분류하였다.

Fig. 2.

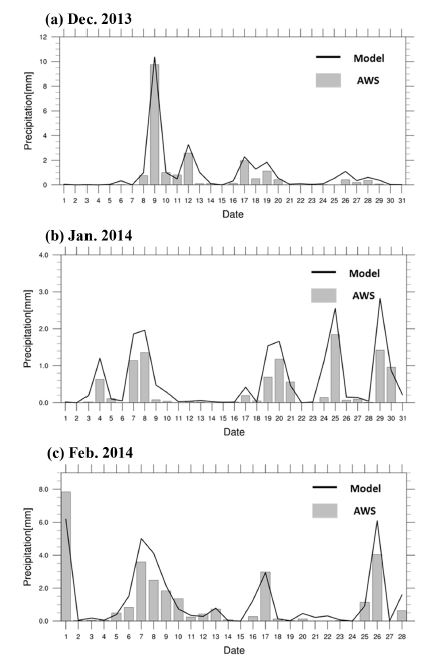
Time series of station averaged daily precipitation amount from Automatic Weather Station AWS observation (grey bar) and +24 h precipitation of daily precipitation averaged for South Korea (solid line). AWS, Automatic Weather Station.

Table 1은 겨울철 전체 강수관측일에 대해 3가지 강수 유형에 따라 분류하고 전체 강수일수 대비 각 유형에 따른 강수일수의 비율을 월별로 나타낸 것이다. 2013년 12월에는 C 유형이 19건(76.0%), L 유형이 4건(16.0%), O 유형은 2건(8.0%)으로 호수효과에 의한 대류성 강수가 가장 많았다. 2014년 1월에는 C 유형이 8건(38.1%), L 유형이 8건(38.1%), O 유형은 5건(23.8%)으로 대류성 및 저기압성 강수가 우세한 가운데 지형성 강수를 포함한 고른 발생을 보였다. 2014년 2월에는 C 유형이 5건(19.2%), L 유형이 6건(23.1%), O 유형은 15건(57.7%)으로 지형성 강수가 가장 많았다. 2013~2014년 DJF 전체 기간에 대해서는 C 유형이 32건(44.4%)으로 가장 높은 빈도를 나타냈고, L 유형은 18건(25.0%), O 유형은 22건(30.6%)으로 나타났다.

Table 1.

The number of days and percent frequency for each precipitation type according to the classified precipitation types during winter season (2013–2014 DJF).

Figure 3은 분류된 각 강수 유형에 대한 이해를 돕기 위하여 선별된 대표적인 사례 일로서, C 유형은 2013년 12월 28일, L 유형은 2014년 2월 1일, O 유형은 2014년 2월 9일을 각각 선정하여 각 날짜의 지상분석일기도, 위성합성영상, AWS 일누적강수량 분포를 제시하였다.

Fig. 3.

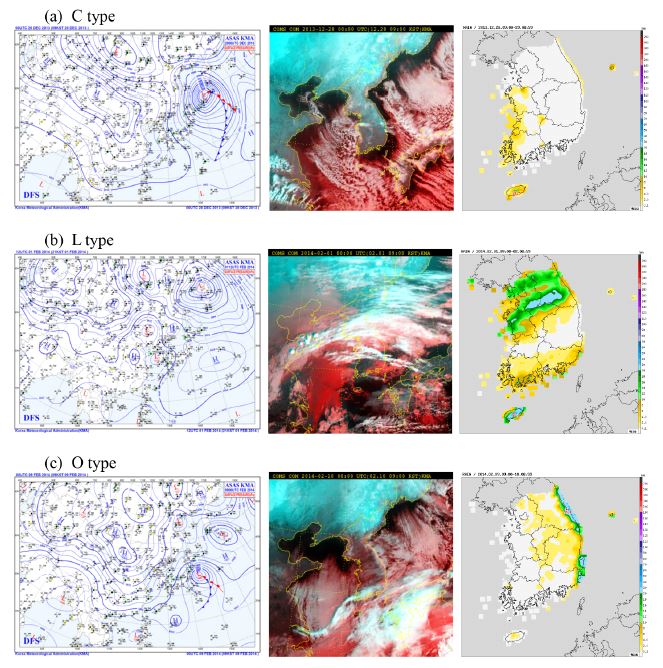
The typical patterns of winter season precipitation in Korean peninsula: Surface analysis chart (left), COMS Satellite image (center), 24 hour accumulated precipitation (right) for days representing features of (a) C type (Convection / Lake effect) on 28 December 2013, (b) L type (Low pressure system) on 1 February 2014, and (c) O type (Orographic effect) on 9 February 2014. COMS, Communication, Ocean and Meteorological Satellite.

3.2 강수 유형별 강수 예측성능 검증

3.2.1 일강수량 산점도 분석

앞에서 분류한 겨울철 강수 유형 3가지에 따라 일강수량 산점도를 분석하였다. Figure 4는 모델의 일별/지점별 예측 일누적강수량과 AWS의 일별/지점별 관측 일누적강수량과의 산점도를 각 예측시간대별로 나타낸 것이다. 모든 강수 유형에서 양의 상관관계(correlation coefficient)를 보이고 있으며, 예측시간이 길어짐에 따라 양의 상관관계가 감소되는 경향도 보이고 있다. 각 유형별로 산점도의 분포를 보면 C 유형은 예측과 관측에서 모두 일누적강수량 20 mm 이하 영역에 집중되어 있는 것으로 보아 다른 유형에 비해 강수량이 적은 유형임을 알 수 있다. 또한 모델의 일누적강수량과 관측 일누적강수량 간의 상관계수는 예측시간 24 h, 48 h, 72 h 각각에 대해서 0.47, 0.41, 0.29의 상관관계를 보였다(Figs. 4a–c). 반면, L 유형은 일누적강수량 40 mm 영역 이하에 주로 분포하면서 예측시간에 따른 상관계수가 각각 0.76, 0.68, 0.66으로 C 유형에 비해 강한 상관관계를 보였다(Figs. 4d–f). 또한 O 유형은 일누적강수량 20~30 mm 영역 이하에 주로 분포하는 동시에 60 mm 부근의 빈도도 일부 나타나는 특징을 보이면서 예측시간별 상관계수가 각각 0.61, 0.52, 0.54로 3가지 유형 중 중간 정도의 상관관계를 보였다(Figs. 4g–i).

Fig. 4.

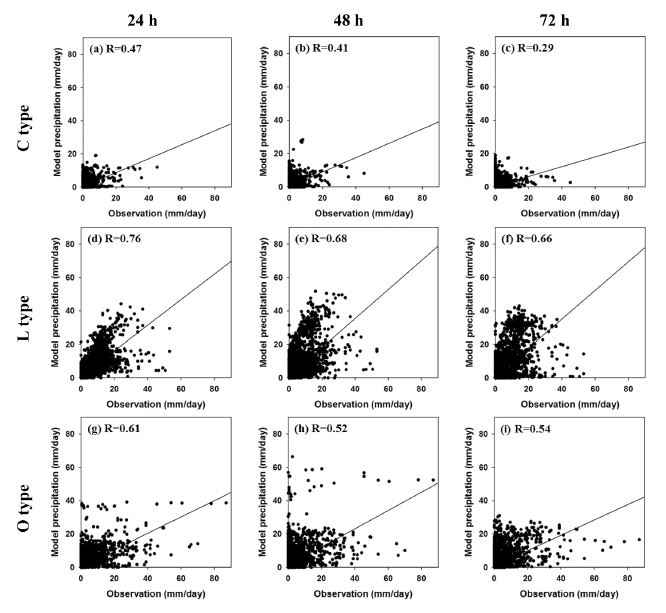
Scatterplots of the daily precipitation obtained from C type, L type, and O type vs AWS precipitation data. Solid line depicts a least square regression line, and letter ‘R’ means correlation coefficient between each type of precipitation and AWS data. AWS, Automatic Weather Station.

산점도는 모델의 예측강수량과 관측강수량 두 가지 변량을 동일한 척도를 가지고 일별/지점별로 일대일 대응하여 비교한다는 점에서 관측강수량과 예측강수량 차이의 정도와 지점별 강수놓침(false negative)과 강수빗나감(false positive)의 빈도가 상관관계에 영향을 주는 주요 요인이 될 것이다. 이러한 점에서 강수 유형별 상관계수의 차이는 Fig. 3에 제시된 각 유형의 대표 사례에서 나타나는 강수의 공간분포와 강수강도 등으로 설명이 될 수 있다. C 유형은 주로 호남 서해안과 충청 일부에 비교적 약한 강수를 기록하는 전형적인 패턴을 가지고 있어서 강수량의 변동폭이 작고 강수영역이 좁은 특징이 있다(Fig. 3a). 따라서, 관측 대비 예측강수의 위치 및 강도 차이로 인한 과대 또는 과소모의 경향과 함께 지점별 강수놓침과 강수빗나감의 빈도가 다른 유형에 비해 많기 때문에 상관계수 값이 가장 낮은 것으로 추정할 수 있다. 반면 L 유형은 저기압이 위치한 지역을 중심으로 광범위한 지역에서 다양한 강도의 강수가 내리기 때문에 상대적으로 예측이 잘되고 있다(Fig. 3b). 또한 O 유형은 강수량의 변동폭은 크고 강수영역은 산맥의 풍상측인 동해안 및 영동지역으로 매우 좁게 형성되고 있어서(Fig. 3c), 지점별 강수빗나감의 빈도가 C 유형보다 많지 않아 각 유형별 상관관계 값이 Fig. 4와 같은 차이를 보인 것으로 판단된다.

3.2.2 정량 지수를 이용한 강수 예측성능 검증

강수 예측성능에 대한 정량적인 분석을 위해 양분 예보를 기반으로 한 검증 지수를 활용하였다. 또한 강수 유형별 일누적강수량을 비교한 산점도 분석을 보완하고자 강수량을 5개(0.1 mm, 1.0 mm, 5.0 mm, 10.0 mm, 20.0 mm day^–1) 임계값으로 나누어 각 정량 지수 분석을 수행하였다. Figure 5는 정량 지수를 산출하기 위한 분할표와 분석에 사용된 Bias, Equitable Threat Score (ETS), Symmetric Extreme Dependency Score (SEDS), Probability Of Detection (POD), False Alarm Ratio (FAR), Success Ratio (SR), 그리고 Critical Success Index (CSI)의 계산 방법에 대해 나타내고 있다.

Fig. 5.

(a) The 2 × 2 contingency table and performance measures for (b) Bias, (c) ETS (Equitable Threat Score), (d) SEDS (Symmetric Extreme Dependency Score), (e) POD (Probability Of Detection), (f) FAR (False Alarm Ratio), (g) SR (Success Ratio), and (h) CSI (Critical Success Index).

Figure 6은 모델의 예측 일누적강수량과 AWS 관측 일누적강수량을 강수임계값 구간별로 비교해 Bias, ETS 및 SEDS를 계산한 것이다. 강수 검증에서 Bias는 관측된 강수에 대한 예측 강수 비율로 1 이상일 때 과대모의, 1 이하일 때 과소모의를 의미한다. Figure 6a에서 보는 바와 같이 C 유형의 경우 0.1 mm day^–1 이상 구간에 대해서 3배에 가까운 매우 큰 Bias를 가지는 것으로 나타나고, 임계값 10.0 mm day^–1까지 단계별로 높아짐에 따라 Bias는 점차 1에 가까워지는 특징을 보였다. 하지만, 20.0 mm day^–1 임계값의 24 h과 72 h 일누적강수량에서는 Bias가 분석되지 않았다. 따라서, 강수가 감지되는 정도의 매우 약한 강수 수준에서는 과대모의 경향이 매우 큰 반면, 강한 강수의 예측 또는 관측사례는 없었던 것으로 보인다. L 유형의 경우는 0.1 mm day^–1 이상 구간에서 약 1.5의 과대모의 경향을 보이지만 1.0 mm day^–1 임계값 이상 구간에서는 1에 가깝게 예측하는 것으로 나타나 3가지 유형 중 가장 Bias가 작은 특징을 보였다. 그러나 20.0 mm day^–1 임계값 이상 구간의 강수에 대해서는 24~48 h 이상 예측에서 과대모의 경향이 뚜렷하였다. O 유형의 경우 0.1~10.0 mm day^–1 임계값 구간에서는 1.5~2배 정도의 과대모의 경향이 일관되게 나타나지만 20.0 mm day^–1 임계값 이상에서는 오히려 과소모의 경향이 나타나는 특징을 보였다. 이처럼 각 유형별/강수임계값별 Bias 분석에서 L 유형의 Bias가 전반적으로 가장 작았으며, C 유형의 Bias가 가장 크게 나타났다. Figure 5b의 Bias 식에 의하면 Bias가 크다는 것은 각 강수량 임계값별 관측수(event observed)보다 예측수(event predicted)가 많다는 의미이다. 또한 분자의 a + b와 분모의 a + c 항에서 강수맞힘(hit)에 해당하는 a가 공통으로 포함되어 있으므로, Bias 크기는 예보를 하였는데 관측되지 않은 강수빗나감에 해당하는 b와 예보를 하지 않았는데 관측도 되지 않은 무강수맞힘에 해당하는 c의 값에 의존한다. 따라서, 5.0 mm day^–1 미만의 구간에서 C 유형과 O 유형이 모두 높은 Bias를 보이는 것은 무강수맞힘보다 강수빗나감의 수가 많기 때문이라고 볼 수 있다. 산점도 분석에서 추정한 바와 같이 비교적 좁은 영역에서의 약한 강수에 대한 강수빗나감이 많았음을 보여주는 것이다. 또한 20.0 mm day^–1 임계구간에서 각 유형별로 Bias의 방향이 일관되지 않고 편차가 매우 크게 나타나는 것은 각 유형별 예측수준 및 관측 샘플 수 차의 영향으로 추정된다.

Fig. 6.

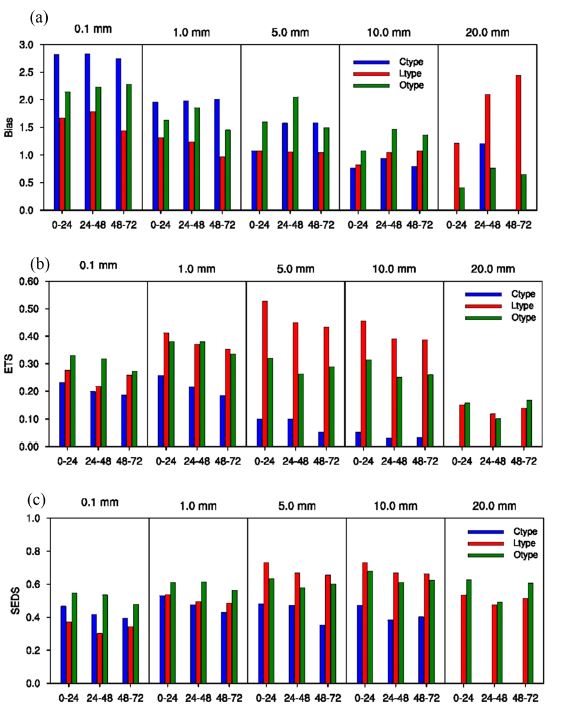
Bias, ETS, and SEDS of daily precipitation prediction (+24 h, +48 h, +72 h) from the Global model for classified precipitation cases, C type, L type, and O type over Korea peninsula against AWS precipitation data with thresholds of 0.1, 1, 5, 10, 20 mm day–1. AWS, Automatic Weather Station.

ETS는 모델의 강수 예측 정확도를 평가하는 값으로 –1/3에서 1 사이의 값을 가지며 1은 완벽한 예보를, 0은 예측 능력이 없음을 의미한다. Figure 6b에서 보는 바와 같이 C 유형의 예측성은 3가지 유형 중 가장 낮은 값을 가지는 것으로 나타났다. 강수 유무를 판별하는 0.1 mm day^–1 임계구간에서도 0.2 내외의 ETS를 기록했으며, 강수량 임계값이 커질수록 급격히 ETS가 낮아져 10.0 mm day^–1 임계구간에서는 0.1 이하의 매우 낮은 예측성을 보였다. 20.0 mm day^–1 임계값에서는 ETS가 0.0으로 예측 능력이 없음으로 나타났다. 이는 앞의 산점도 분석에서 C 유형에서는 20.0 mm day^–1 이상의 강한 강수 사례가 상대적으로 적었으므로 샘플 개수의 영향을 받았을 가능성이 있다. L 유형은 3가지 유형 중 전반적으로 가장 높은 ETS를 보였는데, 특히 5.0, 10.0 mm day^–1 임계구간의 ETS는 0.4~0.5 이상의 값을 보여 예측 성능이 상대적으로 매우 우수한 것을 알 수 있었다. 다만, 20.0 mm day^–1 구간에서는 0.2 이하로 현저하게 예측성이 낮아지는 특징을 보였다. O 유형은 0.1 mm day^–1 구간에서 0.3 내외의 ETS를 보여 3가지 유형 중 예측성이 가장 좋은 것으로 나타났으며, 1.0 mm day^–1 구간에서는 L 유형과 유사한 수준의 양호한 성능을 보였다. 그러나 5.0, 10.0 mm day^–1 임계구간의 ETS는 L 유형보다 크게 낮아지는 특징을 보였다. 따라서, ETS로 본 전반적인 예측성능은 L 유형, O 유형, C 유형 순으로 보는데 무리가 없을 정도로 그 편차가 뚜렷하였다. ETS는 강수맞힘에 초점을 맞춘 TS (Threat Score)에서 우연히 예보가 적중하는 것을 제거한 지수이므로, 총예측수(a + b)와 총관측수(a + c)의 곱을 총표본수(n)로 나눈 값을 분자와 분모에서 각각 차감하여 계산한다. 따라서, 강수 예측성능을 알아보는 지수로 많이 쓰이고 있다. ECMWF (European Centre for Medium-Range Weather Forecasts)에서 제공하는 Forecast User Guide에서는 강수에 대한 ETS를 해석함에 있어서 기억해야 할 점을 다음과 같이 3가지로 언급하고 있다. 첫째, 지점별 관측(강수량계)값과 수치예보모델로부터 산출된 격자점의 값 사이의 공간적 불일치는 ETS를 감소시킨다. 둘째, ETS는 확연한 지리적 변동성을 가지고 있는데, 예를 들어 지형성 강수가 우세한 지역에서 ETS는 더 높은 경향이 있다. 셋째, 대류가 활발한 여름철에 ETS가 두드러지게 감소하는 등 계절순환이 확연하다(ECMWF, 2011). 이 3가지의 해석 상의 핵심 내용들을 보면 이 연구에서 다루고 있는 예측성능이 C 유형에서 상대적으로 낮게 나타나고 L 유형과 O 유형에서 상대적으로 높게 나타나는 것이 일부 설명될 수 있을 것으로 보인다.

한편, Hogan et al. (2009)은 양분 예보에 널리 사용되어온 ETS가 관측 샘플 수에 매우 민감하다고 지적하며, 샘플 개수의 영향을 최소화하여 비교적 공정한 것으로 알려진 SEDS에 의한 평가를 제안한 바 있다. 3가지 유형 모두에서 20.0 mm day^–1 이상의 임계구간에서는 현저히 ETS가 낮아지는 것으로 나타나고, 특히 C 유형의 경우 0.0의 값을 보여 예측성이 전혀 없는 것으로 평가되었는데, 겨울철 강수 유형 중 상대적으로 L 유형과 O 유형에서는 강한 강수 사례가 많았으므로 정확한 성능 판단을 위해서 샘플 개수의 영향을 최소화한 SEDS를 분석하여 추가적으로 강수 예측성을 평가하였다. SEDS는 ETS와 마찬가지로 1은 완벽한 예보, 0은 예보 성능이 없음을 의미한다. Figure 6c에서 보는 바와 같이 SEDS를 통한 강수 정확도 평가에서는 강수 유형 간 성능 차이가 ETS에 비해서 적게 나타났고, 샘플 개수의 영향이 있을 것으로 추정한 20.0 mm day^–1 임계구간에서 ETS가 크게 저하되었던 특징은 완화된 것을 확인할 수 있었다. 하지만, C 유형의 경우 0.1 mm day^–1 구간을 제외한 1.0, 5.0, 10.0 mm day^–1 구간에서는 3가지 유형 중 가장 낮은 SEDS 값을 나타내어 상대적으로 예측성능이 가장 낮음을 일관되게 보여주었으며, 20.0 mm day^–1 이상 구간에서 SEDS가 0.0 인 것으로 보아 관측 샘플이 없었던 것을 알 수 있었다. 반면, L 유형과 O 유형은 전 임계구간에서 비교적 우수한 강수 예측성능을 일관되게 보였다. L 유형은 5.0, 10.0 mm day^–1 임계구간에서는 0.6의 높은 SEDS를 나타내었으나, 약한 강수를 포함하는 0.1, 1.0 mm day^–1 구간에서는 비교적 낮은 성능을 보였다. 특히 0.1 mm day^–1 구간에서 3가지 유형 중 가장 낮은 성능을 보였다. O 유형은 모든 임계구간에서 0.5 이상의 높은 SEDS를 나타내고 있으며 0.1, 1.0, 20.0 mm day^–1 구간에서는 3가지 유형 중 가장 높은 값을 나타내 전반적으로 모든 강수 임계구간에 대한 성능이 양호한 것으로 판단할 수 있다. 강수량의 각 임계구간별로 SEDS를 비교한 것이기 때문에 어떤 유형의 예측성능이 비교적 양호한가의 명시적 판단을 하기에는 무리가 있어 보이는 것이 사실이다. 하지만, 전반적으로 C 유형의 경우가 다른 유형에 비해 Bias의 변동폭도 크고 예측성능이 낮은 것은 명확한 것으로 보인다.

3.2.3 Performance diagram 분석

Bias, CSI, POD, SR을 하나의 그래프에 표출한 performance diagram을 이용하여 강수 유형별 예측성능에 대한 종합적인 분석도 수행하였다. Figure 7에서 보는 바와 같이 그래프에서 y축은 POD, x축은 SR, 실선 곡선은 CSI, 점선은 Bias를 나타낸다. 또한 그래프의 y = x선을 기준으로 위로는 과대모의, 아래로는 과소모의를 의미한다. 따라서 그래프의 오른쪽 상단 모서리 부분으로 갈수록 예측성능이 가장 뛰어난 것임을 의미한다. 각 강수 유형과 임계값은 Fig. 7의 범례와 같이 기호와 색으로 구별하였다. 예측시간별로 표출한 그래프를 보면 모든 유형 및 예측시간에서 약한 강수로 갈수록 과대모의 경향이 뚜렷하고, 강한 강수로 갈수록 Bias가 1에 가까워짐을 알 수 있었다. C 유형의 경우 모든 예측시간에서 3가지 유형 중 CSI가 가장 낮게 나타났으며(0.3 이하), 약한 강수역인 0.1, 1.0 mm day^–1 구간의 Bias는 2 이상으로 3가지 유형 중 과대모의 경향이 가장 강함을 알 수 있다. 다른 두 강수 유형과 달리 5.0 mm day^–1 구간부터 CSI 값이 0.2 이하로 매우 낮게 나타났으며, 10.0 mm day^–1 구간은 0.1보다 조금 크거나 0.1 이하의 값을 보인다. L 유형은 전 예측시간에 걸쳐 3가지 유형 중 가장 높은 CSI를 나타내었고, 5.0 mm day^–1 구간까지 0.5 이상의 CSI, 1.3~2의 Bias를 기록해 다른 유형에 비해 예측성능이 가장 양호하였다. 10.0 mm day^–1 구간에서도 0.4 이상의 CSI와 0.6에 가까운 POD 값을 보이고 있어 예측성능이 유지되는 것을 알 수 있으며, 20.0 mm day^–1 구간에서는 0.3 이상의 POD 값으로 3가지 유형 중 가장 높은 POD를 보여주었다. O 유형은 C 유형과 L 유형의 중간 정도의 성능을 보이고 있는데 1.0 mm day^–1 이하 구간의 CSI는 0.4~0.5, 5.0 mm day^–1 구간의 CSI는 0.3에 가까운 값을 보여주었고 10.0 mm day^–1 구간은 C 유형과 비슷한 수치를 나타내었다. POD는 강수예보를 적극적으로 하면 값이 높아지는 특성을 가지고 있다. 강도가 약한 강수(예: 0.1, 1.0 mm day^–1)에서 상대적으로 POD가 높게 나타나고 있는데, 이는 GRIMs가 강수를 잘 모의하고 있다기 보다는 현재 대부분의 수치예보모델들이 갖는 문제점 중의 하나인 약한 강수를 과대모의하는 문제점이 GRIMs에서도 나타나고 있는 것으로 보인다. 또한 C 유형의 10.0, 20.0 mm day^–1 구간 CSI가 다른 유형에 비해 크게 낮은 것은 강수영역과 시점이 조금만 달라져도 다른 지수에 비해 변화 정도가 매우 큰 CSI의 특성이 반영된 것이라고 볼 수 있다.

Fig. 7.

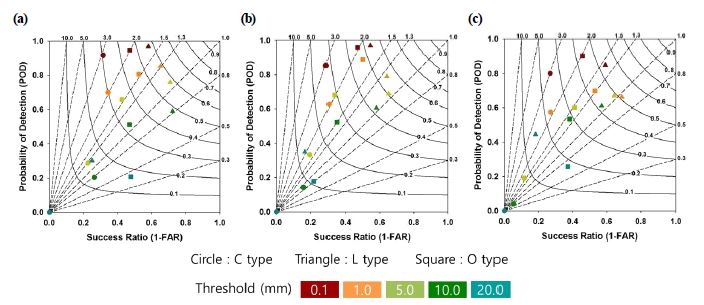
Performance diagram for each forecast time (a) 24 h, (b) 48 h and (c) 72 h. The curved isolines, with associated labels, represent the critical success index, and dashed solid lines represent the bias. The best scores are in the upper right corner; bias values close to one are typically considered optimal.

4. 결 론

본 연구에서는 전지구모델(GRIMs)의 단기(3일) 강수예측에 대한 검증을 2013년 12월~2014년 2월에 해당하는 겨울철에 대하여 평가하였다. 이를 위해, 한반도에서 발생하는 겨울철 강수의 발생 원인을 이론적으로 검토하고, 대상 기간의 강수발생일 전체에 대한 종관분석을 통해 강수 발생 기작에 따라 대류성 강수(C 유형), 저기압성 강수(L 유형), 지형성 강수(O 유형)로 분류하여 통계적 검증을 수행함으로써 GRIMs의 예측 경향을 파악하고자 하였다. 해당기간 중 72일의 강수 사례일에 대해서는 C 유형이 32건(44.4%)으로 가장 높은 빈도를 나타냈고, L 유형은 18건(25.0%), O 유형은 22건(30.6%)으로 나타났다. 월별로는 12월의 경우 C 유형이 76%로 가장 많았으며, 2월에는 O 유형이 57.7%로 가장 많은 것으로 확인되었다.

Bias 분석에서 C 유형과 O 유형은 대체로 과대모의 경향을 보였으나, L 유형은 전체적으로 Bias가 가장 적어 양호한 결과를 보였다. ETS 분석에서는 L 유형이 가장 양호한 성능을 나타내었는데, 5.0, 10.0 mm day^–1 구간에서는 0.4~0.6으로 특히 높은 성능을 보여주었다. 반면, C 유형에 대해서는 전 구간에서 상대적으로 낮은 성능을 보였으며 20.0 mm day^–1 구간에서는 0의 값을 보여 대조적이었다. ETS가 관측 샘플 개수에 영향을 크게 받는다는 점을 고려하여 샘플 개수 의존도를 보완한 SEDS 분석에서는 전 유형에서 0.4~0.6으로 비교적 고르게 높은 예측 성능을 보였으나, 대체로 L 유형, O 유형, C 유형 순으로 높은 값을 보였다. 특히 L 유형의 경우는 ETS에서와 마찬가지로 5.0, 10.0 mm day^–1 구간에서 0.6 이상의 가장 높은 수치를 보여주었다. Performance diagram 분석에서도 전체적으로 과대모의 경향이 나타났으며 특히 강수강도가 약한 구간에서 과대모의 경향이 뚜렷하였다. 또한 L 유형, O 유형, C 유형 순으로 예측성능이 우수한 것으로 나타나 선행 검증지수 분석에서의 경향과 대체로 일치하는 결과를 보였다.

위와 같이 한반도 겨울철 강수 발생 기작별 수치예보모델의 예측 정확도를 다양한 측면에서 평가하고 그 분석결과를 제시하였다. 특히 C 유형의 예측성능이 다른 유형에 비해 낮은 원인에 대해 정량 지수 계산식과 강수영역 및 강수량의 특성을 고려한 분석을 시도하고 ECMWF에서 제공하는 해석 지침을 참고하였다. 향후 과제로서 C 유형은 아격자규모(sub-grid scale) 강수의 경향이 강하므로, L 유형과 O 유형과의 기상현상의 규모 측면에서 원인을 분석하거나 개별 물리과정이 가지는 특성에 대한 연구로의 확장 필요성이 있다. GRIMs는 한국형모델(Korean Integrated Model, KIM) 개발 단계의 KIM 물리패키지가 아직 구성되지 않은 상태에서 물리모듈을 개선하거나 새로운 물리방안을 개발하는데 참고모델로 활용된 바 있다(Hong et al., 2018). Lim et al. (2022)의 연구에 의하면 현재 기상청에서 현업 수치예보모델로 활용하고 있는 KIM은 겨울철 강수현상을 전반적으로 과대모의 하는 경향이 있으며, ECMWF 분석장보다 초기 분석장에서부터 중하층을 습한 상태로 시작한다고 분석하였다. 따라서, 적분 시간이 지남에 따라 q의 증가가 다른 모델 대비 커지는 것으로 나타나는 등 중하층 습수역을 다른 모델들보다 두껍게 모의하게 되어 격자규모 또는 아격자규모의 강수를 더 많이 발생시키고 있음을 밝힌 바 있다. GRIMs의 3가지 강수 유형에 따른 예측성능이 상이한 점을 기반으로 규모 측면의 원인 분석 및 개별 물리과정에 대한 특성 연구로 확장한다면, 그 결과들이 KIM의 겨울철 강수 예측성능 향상을 위한 보다 다양한 민감도 실험의 참고자료가 될 것이며 모델의 최적화에도 기여할 수 있을 것이다.

더불어, 한반도 여름철 등 다른 계절의 강수 발생 기작에 따른 예측성능 검증을 통한 GRIMs의 예측성능 정보는 연구자들에게 수치예보모델의 예측 특성을 파악하거나 개별 물리과정 등에 대한 민감도 실험 등에 기준 자료로 활용될 수 있을 것이다. 또한 다수의 현업 운영모델에 대해서도 강수 발생 기작에 따른 검증을 수행함으로써 모델 간 차이점과 공통점을 파악하고, 하나의 현업 운영모델이 계절에 따른 다양한 강수 발생 기작에서 각각 어떤 예측성능을 보이는지를 파악하는 것도 중요한 시사점을 제공할 것이다. 그 결과들은 예보관의 강수 예보를 위해 필수적인 강수 발생 기작 진단과 수치예보모델 해석에 매우 유용한 정보를 제공할 수 있을 것이다.

Acknowledgments

이 논문은 주저자의 2018년 석사학위 논문을 바탕으로 작성되었습니다. 이 연구 과정에서 당시 다양한 의견과 검증 방법론을 제시하고 도움을 주셨던 (재)한국형수치예보모델개발사업단의 예보검증팀원들에게 감사의 마음을 전합니다.

References

• Barry, R. G., and R. J. Chorley, 2003: Atmosphere, Weather and Climate, 8th ed. Routledge, 101-103 pp. [https://doi.org/10.4324/9780203016206]
• Casati, B., and Coauthors, 2008: Forecast verification: current status and future directions. Meteorol. Appl., 15, 3-18. [https://doi.org/10.1002/met.52]
• Chang, E. C., 2021: Discussion on differences between public and academic understanding of precipitation prediction process and accuracy, In: Proceedings of the Korean Meteorological Society, online conference, 198 pp.
• Cheong, S.-H., K.-Y. Byun, and T.-Y. Lee, 2006: Classification of snowfalls over the Korean Peninsula based on developing mechanism. Atmosphere, 16, 33-48.
• Choi, H.-J., and S. Y. Hong, 2015: An updated subgrid orographic parameterization for global atmospheric forecast models. J. Geophys. Res., 120, 12445-12457. [https://doi.org/10.1002/2015JD024230]
• Chun, H. Y., and J. J. Baik, 1998: Momentum flux by thermally induced internal gravity waves and its approximation for large-scale models. J. Atmos. Sci., 55, 3299-3310. [https://doi.org/10.1175/1520-0469(1998)055<3299:MFBTII>2.0.CO;2]
• Ebert, E. E., U. Damrath, W. Wergen, and M. E. Baldwin, 2003: The WGNE assessment of short-term quantitative precipitation forecasts. Bull. Am. Meteorol. Soc., 84, 481-492. [https://doi.org/10.1175/BAMS-84-4-Ebert]
• ECMWF, 2011: Equitable Threat Score: 6.4 Relative skill of IFS models. Forecast user guide. European Centre for Medium-Range Weather Forecasts. [Available online at https://confluence.ecmwf.int/display/FUG/Equitable+Threat+Score, ].
• Ek, M. B., K. E. Mitchell, Y. Lin, E. Rogers, P. Grunmann, V. Koren, G. Gayno, and J. D. Tarpley, 2003: Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J. Geophys. Res. Atmos., 108, 8851. [https://doi.org/10.1029/2002JD003296]
• Fritsch, J. M., and Coauthors, 1998: Quantitative precipitation forecasting: report of the eighth prospectus development team, US Weather Research Program. Bull. Am. Meteorol. Soc., 79, 285-299. [https://doi.org/10.1175/1520-0477(1998)079<0285:QPFROT>2.0.CO;2]
• Gallus, W. A. Jr., and J. F. Bresch, 2006: Comparison of impacts of WRF dynamic core, physics package, and initial conditions on warm season rainfall forecasts. Mon. Wea. Rev., 134, 2632-2641. [https://doi.org/10.1175/MWR3198.1]
• Han, J., and H.-L. Pan, 2011: Revision of convection and vertical diffusion schemes in the NCEP global forecast system. Wea. Forecasting, 26, 520-533. [https://doi.org/10.1175/WAF-D-10-05038.1]
• Hogan, R. J., E. J. O’Connor, and A. J. Illingworth, 2009: Verification of cloud-fraction forecasts. Q. J. R. Meteorol. Soc., 135, 1494-1511. [https://doi.org/10.1002/qj.481]
• Hong, S. Y., J. Dudhia, and S. H. Chen, 2004: A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon. Wea. Rev., 132, 103-120. [https://doi.org/10.1175/1520-0493(2004)132<0103:ARATIM>2.0.CO;2]
• Hong, S. Y., Y. Noh, and J. Dudhia, 2006: A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Wea. Rev., 134, 2318-2341. [https://doi.org/10.1175/MWR3199.1]
• Hong, S. Y., 2010: A new stable boundary-layer mixing scheme and its impact on the simulated East Asian summer monsoon. Q. J. R. Meteorol. Soc., 136, 1481-1496. [https://doi.org/10.1002/qj.665]
• Hong, S. Y., and Coauthors, 2013: The global/regional integrated model system (GRIMs). Asia-Pac. J. Atmos. Sci., 49, 219-243. [https://doi.org/10.1007/s13143-013-0023-0]
• Hong, S. Y., and Coauthors, 2018: The Korean integrated model (KIM) system for global weather forecasting. Asia-Pac. J. Atmos. Sci., 54, 267-292. [https://doi.org/10.1007/s13143-018-0028-9]
• Iacono, M. J., J. S. Delamere, E. J. Mlawer, M. W. Shephard, S. A. Clough, and W. D. Collins, 2008: Radiative forcing by long-lived greenhouse gases: calculations with the AER radiative transfer models. J. Geophys. Res., 113, D13103. [https://doi.org/10.1029/2008JD009944]
• Korea Meteorological Administration [KMA], 2011: A Hand-Held Forecasting Technique, KMA, 12 pp (in Korean).
• Lee, H., and T.-Y. Lee, 1994: The governing factors for heavy snowfalls in Youngdong area. Asia-Pac. J. Atmos. Sci., 30, 197-218 (in Korean with English abstract).
• Lim, K.-S., and S.-Y. Hong, 2007: Numerical simulation of heavy snowfall over the Ho-Nam province of Korea in December 2005. J. Korean Meteorol. Soc., 43, 161-173.
• Lim, K. S. S., S. Y. Hong, J. H. Yoon, and J. Han, 2014: Simulation of the summer monsoon rainfall over East Asia using the NCEP GFS cumulus parameterization at different horizontal resolution. Wea. Forecasting, 29, 1143-1154. [https://doi.org/10.1175/WAF-D-13-00143.1]
• Lim, Y.-J., W. Choi, B. Y. Koo, Choi, H.-J., Y. C. Kwon and J. S. Ko, 2022: Analysis and implications of prediction characteristics of winter precipitation in 2021, In: Proceedings of the Korean Meteorological Society, 19-21 April 2022.
• Olson, D. A., N. W. Junker, and B. Korty, 1995: Evaluation of 33 years of quantitative precipitation forecasting at the NMC. Wea. Forecasting, 10, 498-511. [https://doi.org/10.1175/1520-0434(1995)010<0498:EOYOQP>2.0.CO;2]
• Park, B. J., 2013: (Column) Interview at a research site - Young-Jun, Kim. Director of Korea Institute of Atmospheric Prediction Systems, The Science & Technology, 525, 86-89 (in Korean).
• Park, R.-S., J.-H. Chae, and S.-Y. Hong, 2016: A revised prognostic cloud fraction scheme in a global forecasting system. Mon. Wea. Rev., 144, 1219-1229. [https://doi.org/10.1175/MWR-D-15-0273.1]
• Sanders, F., 1986: Trends in skill of Boston forecasts made at MIT, 1966–84. Bull. Am. Meteorol. Soc., 67, 170-176.
• Shin, H. H., and S.-Y. Hong, 2015: Representation of the subgrid-scale turbulent transport in convective boundary layers at gray-zone resolutions. Mon. Wea. Rev., 143, 250-271. [https://doi.org/10.1175/MWR-D-14-00116.1]
• Sud, Y. C., J. Shukla, and Y. Mintz, 1988: Influence of land surface roughness on atmospheric circulation and precipitation: a sensitivity study with a general circulation model. J. Appl. Meteorol., 27, 1036-1054. [https://doi.org/10.1175/1520-0450(1988)027<1036:IOLSRO>2.0.CO;2]