[ Article ]

Atmosphere - Vol. 28, No. 1, pp.15-24

ISSN: 1598-3560 (Print) 2288-3266 (Online)

Print publication date 31 Mar 2018

Received 31 Oct 2017 Revised 08 Jan 2018 Accepted 08 Feb 2018

DOI: https://doi.org/10.14191/Atmos.2018.28.1.015

S2S 멀티 모델 앙상블을 이용한 북극 해빙 면적의 예측성

박진경¹⁾^{, *} ; 강현석¹⁾ ; 현유경¹⁾ ; Tetsuo Nakazawa²⁾

1)국립기상과학원 지구시스템연구과
2)일본기상청 기상연구소

Predictability of the Arctic Sea Ice Extent from S2S Multi Model Ensemble

Jinkyung Park¹⁾^{, *} ; Hyun-Suk Kang¹⁾ ; Yu-Kyung Hyun¹⁾ ; Tetsuo Nakazawa²⁾

1)National Institute of Meteorological Sciences, Jeju, Korea
2)Meteorological Research Institute, Japan Meteorological Agency, Tsukuba, Japan

Correspondence to: ^* Jinkyung Park, Earth System Research Division, National Institute of Meteorological Sciences, Korea Meteorological Administration, 33, Seohobuk-ro, Seogwipo-si, Jeju 63568, Korea. Phone: +82-64-780-6713, Fax: +82-64-738-6514 E-mail: kyungii@korea.kr

Abstract

Sea ice plays an important role in modulating surface conditions at high and mid-latitudes. It reacts rapidly to climate change, therefore, it is a good indicator for capturing these changes from the Arctic climate. While many models have been used to study the predictability of climate variables, their performance in predicting sea ice was not well assessed. This study examines the predictability of the Arctic sea ice extent from ensemble prediction systems. The analysis is focused on verification of predictability in each model compared to the observation and prediction in particular, on lead time in Sub-seasonal to Seasonal (S2S) scales. The S2S database now provides quasi-real time ensemble forecasts and hindcasts up to about 60 days from 11 centers: BoM, CMA, ECCC, ECMWF, HMCR, ISAC-CNR, JMA, KMA, Meteo France, NCEP and UKMO. For multi model comparison, only models coupled with sea ice model were selected. Predictability is quantified by the climatology, bias, trends and correlation skill score computed from hindcasts over the period 1999 to 2009. Most of models are able to reproduce characteristics of the sea ice, but they have bias with seasonal dependence and lead time. All models show decreasing sea ice extent trends with a maximum magnitude in warm season. The Arctic sea ice extent can be skillfully predicted up 6 weeks ahead in S2S scales. But trend-independent skill is small and statistically significant for lead time over 6 weeks only in summer.

Keywords:

Sea ice extent, S2S, multi model ensemble

1. 서 론

기후 변화에 따라 북극 해빙은 급격하게 감소하고 있으며 북극해와 인접한 고위도 지역의 환경 또한 빠르게 변하고 있다. 1979~1996년 9월의 해빙 면적의 감소 경향은 2.2%/decade이었으나 1979~2007년 10.2%/decade로 해빙의 감소 경향은 가속화되고 있다(Comiso et al., 2008). 해빙 관측 이래 2012년 9월 3.39 × 10⁶ km²의 최소 해빙 면적을 기록하는 등 해빙 면적의 감소 경향이 뚜렷하게 나타나고 있다. 북극 해빙은 중위도 대기 순환과 강수 패턴을 변동시키며(Sewall and Sloan, 2004), 여름철 북대서양과 북태평양의 해빙 농도가 감소할 경우 겨울철 북대서양 진동(North Atlantic Oscillation, NAO)과 북극 진동(Arctic Oscillation, AO) 음의 위상을 강화시키는 역할을 한다(Wu and Zhang, 2010). 특히 여름철 북극 해빙의 감소는 로스비파를 강화시켜 북극의 찬 공기의 유입을 유도하여 동아시아의 겨울철 기온을 감소시키고(Honda et al., 2009), 한파의 발생을 유도하는 등(Cohen et al., 2013; Tang et al., 2013) 극 지역 뿐만 아니라 중위도 지역까지 영향을 미치는 것으로 알려져 있다. 이처럼 북극의 기후 변화와 이와 관련된 빙권의 변화는 중위도 및 유라시아 지역의 겨울철 기후 변동을 이해하는 데 중요한 역할을 하고 있으며 계절 예측의 향상을 위해 선행되어야 하는 부분이다.

기후예측모델을 이용하여 계절 규모의 북극 해빙 예측성을 확인하기 위한 여러 선행 연구가 진행되었다(e.g., Wang et al., 2012; Sigmond et al., 2013). 이러한 연구들은 주로 단일 모형을 이용하여 해빙의 계절 규모 예측에 초점을 맞추어 진행되었는데, 예측성은 계절에 따른 차이가 있으며 여름은 약 2~3개월, 그 외 계절은 1개월 이하의 예측성을 확인하였다. Sigmond et al. (2016)은 북극해를 해역별로 구분하여 트렌드와 초기장의 영향에 따른 예측성을 평가하였고, Merryfield et al. (2013)은 계절예측시스템인 CFSv2 (Climate Forecast System version 2)와 CanSIPS (Canadian Seasonal to Interannual Prediction System)를 이용하여 선행 연구와 일치한 결과를 도출하였고, 두 모형의 결합된 예측성이 단일 모형보다 뛰어남을 확인하였다. 또한 기후값을 이용한 초기화 기법(Guemas et al., 2016), 적설 초기화 기법을 통해 겨울철 북극 기온과 해빙농도의 계절 예측을 향상시키는 연구(Jeong et al., 2013; Shim et al., 2013)들이 진행되었다.

단중기 예보와 장기 예보의 사이에는 예측 공백 기간이 존재한다. 계절 내-계절 규모가 이 규모에 해당하며 이음새 없는 예측을 위해 2주~2개월의 예측성 향상을 위한 연구인 S2S (Sub-seasonal to Seasonal) 프로젝트가 진행되고 있다(Vitart et al., 2012). 최근 많은 연구들은 기상과 기후 분야 간의 협동 연구를 강조해왔다(e.g., Hurrell et al., 2009; Brunet et al., 2010). WMO CAS (World Meteorological Organization Commission on Atmospheric Sciences)는 세계기상연구 프로그램(World Weather Research Program, WWRP)과 세계기후연구프로그램(World Climate Research Program, WCRP)의 합동과학위원회와 국제 연구기반에 대한 협업 체계 구성을 발의하였고 2012년 계절 내 규모의 예측성 향상에 초점을 둔 S2S 프로젝트의 설립이 승인되었다. 이 프로젝트는 중기 규모와 계절 규모 간의 간극을 줄이고 현업 예보 기관의 예측 기술 개선과 계절 내 규모의 잠재적 예측성을 평가하는 것을 목표로 한다. 2015년부터 유럽중기예보센터(The European Centre for Medium-Range Weather Forecasts, ECMWF)와 중국기상청(China Meteorological Administration, CMA)에서 S2S 프로젝트에 참여하고 있는 현업 기관의 자료를 공유하기 위해 데이터베이스를 구축하였고, 기관 별 대기 및 해양, 해빙 등의 변수 자료를 제공하고 있다. S2S 규모에 대한 이해는 기후 모델의 개선 및 정책 결정을 위한 사회경제적인 측면에서 중요하므로 이에 대한 지속적인 연구가 필요하다.

본 연구에서는 S2S 데이터베이스 자료를 이용하여 현업 예측 모형들이 가지고 있는 북극 해빙 예측성을 분석하여 현재의 해빙 예측 수준을 제시하고자 하였다. 계절 내-계절 규모에서의 북극 해빙 농도와 해빙 면적의 기후값과 변화 경향을 분석하고 단일 모형과 다중 모델 앙상블의 예측성을 검증하였다. 선행 연구의 월 단위의 예측 선행 시간(Lead time)을 S2S 규모 내에서 주 단위로 세분화하여 1~6주의 예측성을 분석하였다.

2. 자료 및 분석 방법

2.1 자료

S2S 데이터베이스는 총 11개 기관, BoM (Bureau of Meteorology), CMA (China Meteorological Administration), CNR-ISAC (Institute of the Italian National Research Council-The Institute of Atmospheric Sciences and Climate), ECCC (Environment and Climate Change Canada), ECWWF (The European Centre for Medium-Range Weather Forecasts), HMCR (Hydrometcentre of Russia), JMA (Japan Meteorological Agency), KMA (Korea Meteorological Administration), Meteo France (이하 METFR), NCEP (National Centers for Environmental Prediction, UKMO (UK Met Office)의 예측 자료(Forecast)와 과거기후모의자료(Hindcast)를 준-실시간으로 제공하고 있다(http://apps.ecmwf.int/datasets/data/s2s/, http://s2s.cma.cn/). 이 중 해빙 모델과 결합된 시스템인 CMA의 BCC-CSM1.2, KMA의 GloSea5, METFR의 CNRM-CM 6.0, NCEP의 CFSv2와 과거 기후 모의 자료를 이용하였고 다중 모델 앙상블(MME) 결과를 분석하였다. 분석에 이용한 예측시스템은 대기-해양-해빙의 결합 모형으로 각 모형의 대기 모델은 상이하며, CMA와 NCEP 모형의 해양모델과 해빙 모델은 GFDL MOM4와 GFDL SIS로 동일하다. 각 기관의 시스템명과 시스템의 구성은 Table 1과 같다.

Table 1.

Summary of model configuration.

본 연구에 사용된 과거 기후 모의 자료는 모형들의 동등한 비교를 위하여 공통된 기간인 1999~2009년의 11년이며, 초기장은 매월 1, 15일(KMA는 1, 17일) 월 2회, 예측 선행 시간은 1~42일, 앙상블 멤버는 3개이다. 해상도는 위경도 1.5^o로 내삽하여 사용하였다. 선행 시간은 초기화 시점과 예측 시점의 시간 차이를 뜻하며 Lead 1은 예측 날짜로부터 1~7일, Lead 2-Lead 6은 각각 8~14일, 15~21일, 22~28일, 29~35일, 36~42일에 해당하는 자료를 이용하여 7일 단위로 구분하였다.

북극 해빙의 예측성을 평가하기 위해 NSIDC (The National Snow and Ice Data Center)의 NOAA/NSIDC Climate Data Record of Passive Microwave Sea Ice Concentration 관측 자료를 사용하였다(Peng et al., 2013). 관측 자료는 북극해를 중심으로 고위도-중위도 영역의 25 km 해상도를 가지며, S2S 데이터베이스 자료의 해상도인 위경도 1.5^o로 변환하여 분석하였다.

2.2 분석 방법

해빙 농도는 0~1의 무차원 수 또는 0~99%의 값으로 표현된다. 해빙 면적(SIE, Sea Ice Extent)은 해빙 농도(Sea Ice Concentration)가 15% 이상인 격자의 북반구 총 면적으로 정의하였다. 해빙의 유무를 결정하는 기준 농도인 15%는 가장 널리 사용되는 농도로써, 해빙이 대기 조건에 영향을 받더라도 얼음 상태를 유지할 수 있는 한계값이다(Parkinson and Cavalieri, 2008).

예측성을 평가하기 위해 아노말리상관계수(Anomaly Correlation Coefficient, ACC)를 사용하였다.

A C C i, τ = 1 N ∑ j = 1 N F i j τ - F ¯ i τ O i j - O ¯ i 1 N ∑ j = 1 N F i j τ - F ¯ i j 2 1 N ∑ j = 1 N O i j - O ¯ i 2

(1)

F는 모형의 예측 자료, O는 관측 자료를 의미한다. i는 각 월에 해당하는 값이고, j는 분석 기간인 총 11년(1999~2009년)의 각 해에 해당하는 값, τ는 예측 선빙 면적을 과소모의하고 겨울철 해빙 면적을 과대모의하여 해빙 면적의 계절 변동을 크게 모의하였다. 관행 시간에 해당하는 값(1-6)이다. ACC는 모형과 관측자료의 선형 상관관계를 나타내는 지수로써 −1에서 1의 값을 가지며 1의 값에 가까울수록 모형의 예측성이 우수함을 나타낸다. 위 식에서 계산된 상관계수는 해빙의 트렌드를 포함하므로 트렌드를 제거한 예측성을 함께 검증하여 비교하였다.

3. 결 과

3.1 기후값

관측과 각 모형들의 월별 북극 해빙 면적을 Fig. 1에 나타내었다. CMA의 해빙 면적은 관측과의 차이가 크므로 CMA를 제외한 다중 모델 앙상블인 MME_C를 추가적으로 분석하였다. MME_C는 관측의 기후값과 가장 유사하게 모의하였고 개별 모형 중에서는 METFR이 해빙 면적의 계절 변동을 관측과 유사하게 모의하였다. CMA는 관측과 비교하여 모든 계절에 대해 과소모의하나 계절 변동은 관측과 유사하다. 또한 8월부터 해빙 면적이 급격히 감소하여 9월에는 거의 해빙이 존재하지 않는다. KMA와 NCEP은 여름철 해측과 MME를 포함한 모형들의 최대 해빙 면적은 3월, 최소 해빙 면적은 9월에 나타나지만 S2S 규모에서 KMA는 8월을 최소 해빙 면적으로 모의하였고 NCEP은 2월을 최대 해빙 면적으로 모의하여 관측과의 차이가 존재하였다.

Fig. 1.

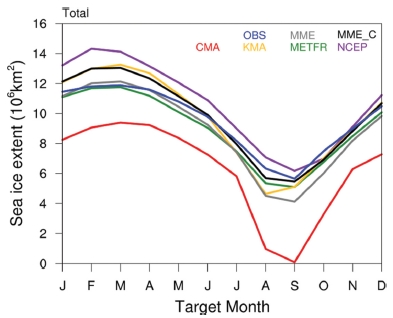
Climatology of monthly sea ice extent from observation (OBS) and models, multi-model ensemble mean (MME) on Lead 1-Lead 6. MME_C is MME, exclusive of CMA.

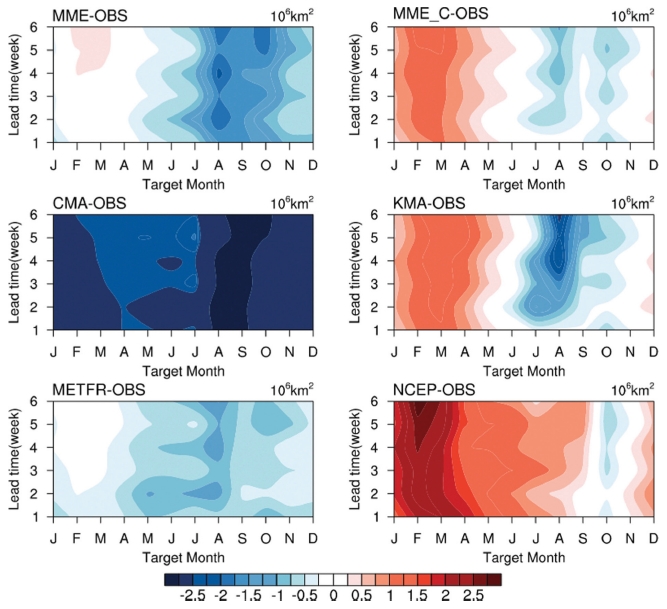
Fig. 2는 선행 시간에 따른 관측과 모형의 월별 북극 전체의 해빙 면적 차이이다. 모든 월과 선행 시간에서의 평균 절대값 오차는 MME_C가 0.53 × 10⁶ km²로 가장 작고, 개별 모형 중에서는 METFR이 0.55 × 10⁶ km²로 작으며, CMA는 3.27 × 10⁶ km²로 가장 크게 나타났다. CMA는 8월 Lead 1에서 최대 −6.09 × 10⁶ km²의 차이가 나타나며 모든 월과 선행 시간에 대하여 해빙 면적을 작게 모의한다. METFR은 모든 월에 대해 해빙 면적을 작게 모의하였고 KMA와 NCEP은 겨울철에는 과대모의, 여름철에는 과소 모의하는 특징이 있었다.

Fig. 2.

Bias of monthly sea ice extent with observation on lead time.

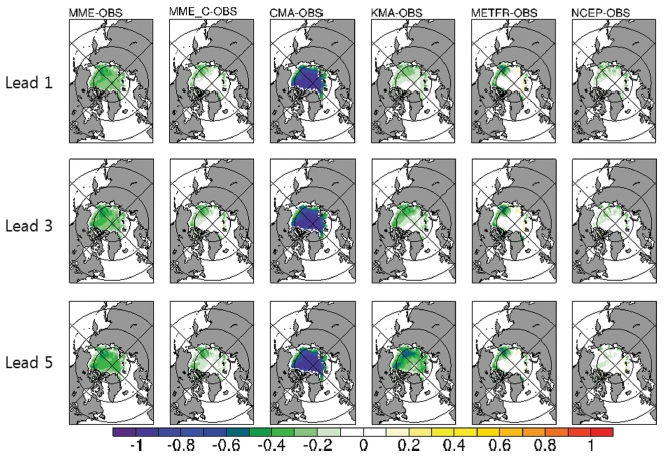
북극의 해역 별 해빙 농도를 확인하기 위하여 해빙 면적이 최대가 되는 3월(Fig. 3)과 최소가 되는 9월(Fig. 4)의 관측과의 해빙 농도 오차 분포를 분석하였다. 3월의 해빙 농도는 해빙의 경계에서 오차가 나타나며 모든 모형에서 오호츠크 해의 해빙 농도를 낮게 모의한다. CMA는 바렌츠 해와 래브라도 해, 그린란드 주변 해역의 해빙 농도를 높게 모의하였고 KMA와 NCEP은 예측 선행 시간이 길어지면서 바렌츠 해와 그린란드 주변 해역의 양의 오차가 증가하는 경향이 있었다. 9월의 해빙 농도는 음의 오차가 뚜렷하게 나타났다. MME에서 나타난 음의 오차는 CMA의 낮은 해빙 농도 영향이며 MME_C에서 오차가 감소하였다. CMA는 북극해 중심에서도 0의 해빙농도를 모의하여 최대 −1의 오차가 나타났고 KMA는 예측 선행 시간이 지나면서 동시베리아 해, 보퍼트 해, 척치 해의 음의 오차가 점차 증가하였다. NCEP은 예측 선행 시간이 지나면서 3월(Fig. 3)의 결과와 동일하게 해빙 농도가 점차 증가하여 음의 오차가 감소하고 반대로 양의 오차가 증가하는 경향을 확인하였다.

Fig. 3.

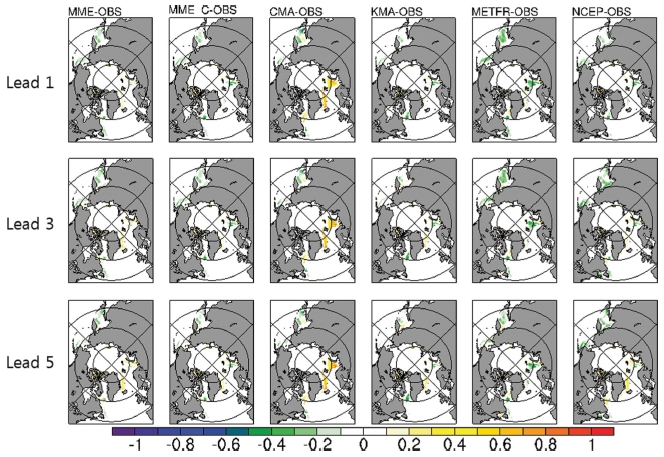
Mean bias of March sea ice concentration from models and multi-model ensemble mean (MME) on Lead 1, Lead 3 and Lead 5. MME_C is MME, exclusive of CMA.

Fig. 4.

Same as in Fig. 3, but for September.

3.2 연변동 및 트렌드

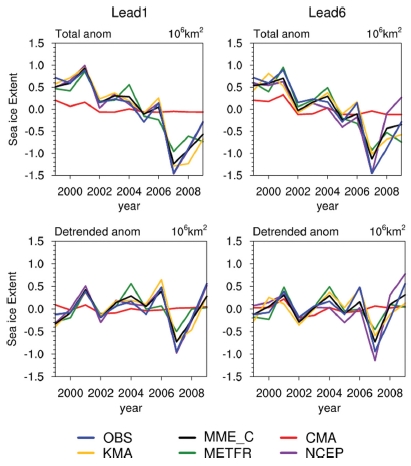
여름과 겨울철 북극 해빙 면적의 변화를 알아보기 위해 Lead 1과 Lead 6의 3월(Fig. 5)과 9월(Fig. 6) 아노말리 시계열을 분석하였다. CMA를 제외한 MME_C가 MME보다 유의한 결과로 판단되어 이하 MME 결과를 제시하지 않았다.

Fig. 5.

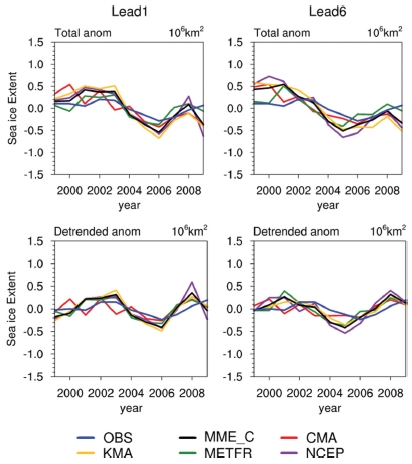
Total anomalies (top) and detrended anomalies (bottom) of March sea ice extent from observation (OBS) and models, multi-model ensemble mean exclusive of CMA (MME_C) on Lead 1 (left) and Lead 6 (right).

Fig. 6.

Same as in Fig. 5, but for September.

관측 자료의 겨울철 북극 해빙 면적의 연변동이 뚜렷하지 않아 모든 모형들의 연변동이 관측과의 차이가 있었고, 여름철의 연변동은 관측과 유사하게 모의하였다. 트렌드 제거 전과 후 모두 관측과 유사하게 나타났고 Lead 6에서는 관측과의 차이가 증가하였다. 선행 시간이 증가하더라도 CMA를 제외한 모든 모형이 여름철의 2001년 양의 아노말리와 2007년의 음의 아노말리와 같은 큰 변동을 모의하였고 특히 NCEP은 관측과 거의 일치하였다.

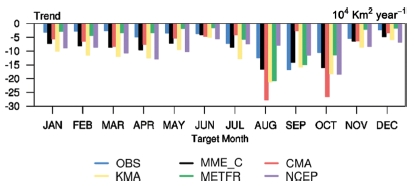
북극 해빙 면적의 월별 감소 경향을 알아보기 위해 11년 동안의 트렌드를 분석하였다(Fig. 7). 다소 짧은 기간임에도 불구하고 해빙 면적의 감소가 뚜렷하게 나타나며, 모든 모형들이 해빙의 감소 경향을 모의하였다. 북극 모든 해역에서 8~10월은 가장 뚜렷한 감소 경향을 나타내는 기간으로(Parkinson and Cavalieri, 2008; Kim et al., 2014), 여름철 해빙의 감소 경향은 약 −15 × 10⁴ km²/year로 봄, 가을에 비해 약 2~3배 빠르게 감소하는 것을 확인할 수 있다. METFR을 제외한 모형들이 관측에 비해 감소 경향을 크게 모의하는 편이며, CMA의 9월 감소 경향이 매우 작게 나타나는 것은 9월 해빙 면적이 0에 가까워 감소할 해빙 면적이 없기 때문이다.

Fig. 7.

Trend of monthly sea ice extent from observation (OBS) and models, multi-model ensemble mean exclusive of CMA (MME_C) on Lead 1~Lead 6.

3.3 예측성

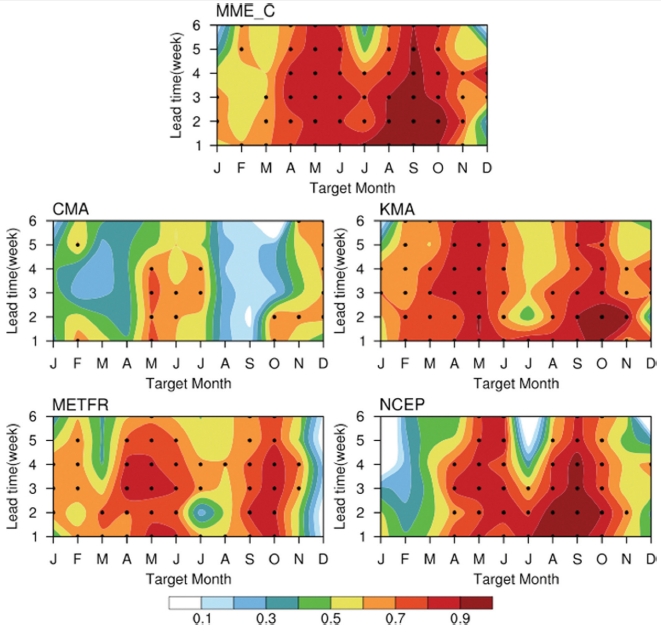
모형들의 예측성을 평가하기 위해 선행 시간에 따른 월별 ACC (Fig. 8)와 트렌드를 제거한 ACC (Fig. 9)를 분석하였다. MME_C와 개별 모형 중에서는 KMA의 예측성이 높으며 모든 모형에서 계절에 따른 예측성의 차이가 존재한다. 8~10월, 4~6월의 예측성이 높고 7월과 12~1월의 예측성이 낮다. 특히 CMA를 제외한 모든 모형에서 9월의 예측성은 통계적으로 유의하며 Lead 6까지 0.8 이상, 4~6월의 예측성 또한 Lead 6까지 0.6 이상으로 높다. 7월과 12~1월의 예측성은 선행 시간에 따라 감소하여 METFR은 Lead 1에서 0.1, NCEP은 Lead 6에서 0.3으로 다른 계절과 비교하여 낮은 편이다. 즉, 북극 해빙 면적이 최대 또는 최소가 되는 시기의 예측성이 높고 해빙이 생성 또는 융해되는 시기의 예측성이 낮게 나타났다. S2S 규모에 해당하는 Lead 3~6의 여름철과 겨울철의 해빙 면적 예측성은 Lead 1~2의 예측성과 유사하다.

Fig. 8.

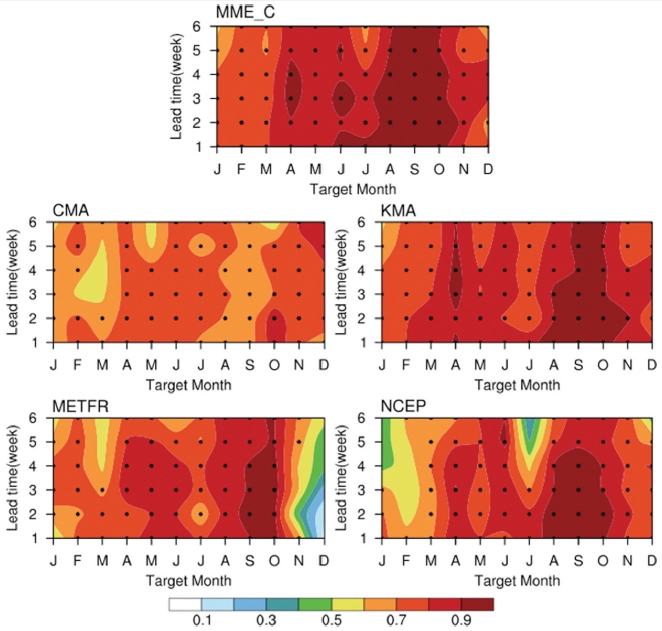
Anomaly correlation coefficient of sea ice extent between observation and models, multi-model ensemble mean exclusive of CMA (MME_C) for total anomalies. The ACC are plotted on target month and lead time. Black dots represent statistical significance of a linear correlation coefficient at the 95% confidence level.

Fig. 9.

Same as in Fig. 8, but for detrended anomalies.

트렌드를 제거할 경우, 선행 연구인 Wang et al. (2012), Merryfield et al. (2013), Sigmond et al. (2013)의 결과와 동일하게 제거 전보다 예측성이 낮아지며 이에 따른 계절별 예측성 차이가 커진다. 예측성이 높은 계절인 여름철은 트렌드를 제거하더라도 CMA를 제외한 모든 모형에서 Lead 6까지 0.6 이상의 예측성이 높게 나타나지만 해빙의 변화가 큰 6~7월과 12~1월에는 선행 시간에 따라 예측성이 낮아진다. 트렌드 제거 전의 예측성과 동일하게 MME_C와 개별 모형 중에서는 KMA의 예측성이 높게 나타났다.

4. 요약 및 토의

본 연구에서는 S2S 데이터베이스로부터 수집한 현업 예측 모형들의 S2S 규모 내 북극 해빙 예측성을 평가하였다. 각 모형들을 관측과 비교하여 해빙 면적 기후값과 연변동, 아노말리상관계수를 통해 예측성을 분석하였다. S2S 규모에서의 북극 해빙 면적은 계절에 따라 관측과의 차이가 있었고 일부 해역에서 선행시간에 따라 해빙 농도의 오차가 증가하는 경향이 있었다. 북극 전체의 해빙 면적 예측성은 6주 이상이며, 트렌드를 제거하더라도 여름철의 예측성은 높게 나타났다. 이와 같이, S2S 규모에서 계절예측시스템이 모의하는 북극 해빙 자료는 계절에 따른 차이는 있으나 계절 규모 이상의 장기 예측을 위한 예측 인자로 활용 가능할 것으로 판단된다. 모든 모형에서 계절별 예측성 차이가 존재하였고, 트렌드는 예측성에 영향을 주는 주요한 요소임을 확인하였다. 이 결과는 선행 연구인 Wang et al. (2012), Sigmond et al. (2013)와 일치하나 모형들의 분석 기간과 초기장, 앙상블 멤버 수의 통일로 인한 제약으로 선행 연구와 비교하여 다소 낮은 예측성을 나타냈다. 본 연구 결과에 포함시키지는 않았으나 METFR과 NCEP의 분석 기간과 초기장, 앙상블 멤버 수를 확대하였을 때 예측성이 증가하는 것을 확인하였다. 그러나 일부 모형에 대해서만 분석하였으므로 이에 대한 추가적인 연구가 필요할 것으로 보인다. MME는 모든 계절, 모든 예측 선행 기간에 대해 상관계수가 0.7 이상으로 높았고, KMA 또한 높은 예측성을 나타냈다. 개별 모형과 비교하여 MME의 예측성이 높았으나 보다 정확한 MME 분석을 위해서는 해빙 모델과 결합된 모형의 개수를 늘려야 할 것으로 판단된다.

북극 해빙의 예측성은 계절마다 다른 요소가 복합적으로 작용하여 예측성을 감소시키는 원인에 대한 다양한 연구 결과가 보고되었다. 선행 연구에서는 모델이 모의하는 계절 변동, 예측성의 지속성을 좌우하는 초기장, 해빙 두께와 해빙 부피 등을 원인으로 분석하였다(Wang et al., 2012; Chevallier et al., 2013; Peterson et al., 2015). 또한 적분 시간이 증가하면서 모델 내에서 발생하는 climate drift도 관측과의 오차를 유도하는 중요한 요인 중 하나이다(Gupta et al., 2012). 추후 해빙의 예측성 향상을 위하여 예측성에 영향을 미치는 기후 인자와 앙상블 멤버 및 모형을 확대한 다중모델앙상블 분석이 이루어질 예정이다.

Acknowledgments

본 연구는 국립기상과학원 ‘기상업무지원기술개발연구(NIMS-2016-3100)’의 일환으로 수행되었습니다.

References

Brunet, G., and Coauthors, (2010), Collaboration of the Weather and Climate Communities to Advance Subseasonal-to-Seasonal Prediction, Bull. Amer. Meteor. Soc, 91, p1397-1406. [https://doi.org/10.1175/2010BAMS3013.1]
Chevallier, M., D. Salas, Y. Mélia, A. Voldoire, M. Déqué, and G. Garric, (2013), Seasonal forecasts of the pan-Arctic sea ice extent using a GCM-based seasonal prediction system, J. Climate, 26, p6092-6104. [https://doi.org/10.1175/JCLI-D-12-00612.1]
Cohen, J., J. Jones, J. C. Furtado, and E. Tziperman, (2013), Warm Arctic, cold continents: a common pattern related to Arctic sea ice melt, snow advance, and extreme winter weather, Oceanography, 26, p150-160. [https://doi.org/10.5670/oceanog.2013.70]
Comiso, J. C., C. L. Parkinson, R. Gersten, and L. Stock, (2008), Accelerated decline in the Arctic sea ice cover, Geophys. Res. Lett, 35, L01703. [https://doi.org/10.1029/2007GL031972]
Guemas, V., M. Chevallier, M. Déqué, O. Bellprat, and F. Doblas-Reyes, (2016), Impact of sea ice initialization on sea ice and atmosphere prediction skill on seasonal timescales. Geophys, Res. Lett, 43, p3889-3896. [https://doi.org/10.1002/2015GL066626]
Gupta, A. S., L. C. Muir, J. N. Brown, S. J. Phipps, P. J. Durack, D. Monselesan, and S. E. Wijffels, (2012), Climate Drift in the CMIP3 Models, J. Climate, 25, p4621-4640. [https://doi.org/10.1175/JCLI-D-11-00312.1]
Honda, M., J. Inoue, and S. Yamane, (2009), Influence of low Arctic sea-ice minima on anomalously cold Eurasian winters. Geophys, Res. Lett, 36, L08707. [https://doi.org/10.1029/2008GL037079]
Hurrell, J., G. A. Meehl, D. Bader, T. L. Delworth, B. Kirtman, and B. Wielicki, (2009), A unified modeling approach to climate system prediction, Bull. Amer. Meteor. Soc, 90, p1819-1832. [https://doi.org/10.1175/2009BAMS2752.1]
Jeong, J.-H., H. W. Linderholm, S.-H. Woo, C. Folland, B.-M. Kim, S.-J. Kim, and D. Chen, (2013), Impacts of snow initialization on subseasonal forecasts of surface air temperature for the cold season, J. Climate, 26, p1956-1972. [https://doi.org/10.1175/JCLI-D-12-00159.1]
Kim, B.-M., E. Jung, G.-H. Lim, and H.-K. Kim, (2014), Analysis on Winter Atmosphereic Variability Related to Arctic Warming, Atmosphere, 24, p131-140, (in Korean with English abstract). [https://doi.org/10.14191/Atmos.2014.24.2.131]
MacLachlan, C., and Coauthors, (2015), Global Seasonal forecast system version 5 (GloSea5): a high-resolution seasonal forecast system, Quart. J. Roy. Meteoro. Soc, 141, p1072-1084. [https://doi.org/10.1002/qj.2396]
Merryfield, W. J., W.-S. Lee, W. Wang, M. Chen, and A. Kumar, (2013), Multi-system seasonal predictions of Arctic sea ice, Geophys. Res. Lett, 40, p1551-1556. [https://doi.org/10.1002/grl.50317]
Parkinson, C. L., and D. J. Cavalieri, (2008), Arctic sea ice variability and trends, 1979-2006, J. Geophys. Res, 113, C07003. [https://doi.org/10.1029/2007JC004558]
Peng, G., M. N. Meier, D. J. Scott, and M. H. Savoie, (2013), A long-term and reproducible passive microwave sea ice concentration data record for climate studies and monitoring, Earth Syst. Sci. Data, 5, p311-318. [https://doi.org/10.5194/essd-5-311-2013]
Peterson, K. A., A. Arribas, H. T. Hewitt, A. B. Keen, D. J. Lea, and A. J. McLaren, (2015), Assessing the forecast skill of Arctic sea ice extent in the GloSea4 seasonal prediction system, Climate Dyn, 44, p147-167. [https://doi.org/10.1007/s00382-014-2190-9]
Saha, S., and Coauthors, (2014), The NCEP Climate Forecast System version 2, J. Climate, 27, p2185-2208. [https://doi.org/10.1175/JCLI-D-12-00823.1]
Sewall, J. O., and L. C. Sloan, (2004), Less ice, less tilt, less chill: The influence of a seasonally ice-free Arctic Ocean and reduced obliquity on early Paleogene climate, Geology, 32, p477-480. [https://doi.org/10.1130/g20295.1]
Shim, T., J.-H. Jeong, B.-M. Kim, S.-J. Kim, and H.-K. Kim, (2013), Development of dynamical seasonal prediction system for northern winter using the cryospheric condition of late autumn, Atmosphere, 23, p73-83, (in Korean with English abstract). [https://doi.org/10.14191/Atmos.2013.23.1.073]
Sigmond, M., J. C. Fyfe, G. M. Flato, V. V. Kharin, and W. J. Merryfield, (2013), Seasonal forecast skill of Arctic sea ice areain a dynamical forecast system, Geophys. Res. Lett, 40, p529-534. [https://doi.org/10.1002/grl.50129]
Sigmond, M., M. C. Reader, G. M. Flato, W. J. Merryfield, and A. Tivy, (2016), Skillful seasonal forecasts of Arctic sea ice retreat and advance dates in a dynamical forecast system, Geophys. Res. Lett, 43, p12457-12465. [https://doi.org/10.1002/2016GL071396]
Tang, Q., X. Zhang, X. Yang, and J. A. Francis, (2013), Cold winter extremes in northern continents linked to Arctic sea ice loss. Environ, Res. Lett, 8, 014036. [https://doi.org/10.1088/1748-9326/8/1/014036]
Vitart, F., A. W. Robertson, and D. L. T. Anderson, (2012), Subseasonal to seasonal prediction project: Bridging the gap between weather and climate, WMO Bull, 61, p23-28.
Voldoire, A., and Coathors, (2013), The CNRM-CM5.1 global climate model: description and basic evaluation, Climate Dyn, 40, p2091-2121. [https://doi.org/10.1007/s00382-011-1259-y]
Wang, W., M. Chen, and A. Kumar, (2012), Seasonal prediction of Arctic sea ice extent from a coupled dynamical forecast system, Mon. Wea. Rev, 141, p1375-1394. [https://doi.org/10.1175/MWR-D-12-00057.1]
Wu, Q., and X. Zhang, (2010), Observed forcing-feedback processes between Northern Hemisphere atmospheric circulation and Arctic sea ice coverage, J. Geophys. Res, 115, D14119. [https://doi.org/10.1029/2009JD013574]
Wu, T., and Coauthors, (2014), An overview of BCC climate system model development and application for climate change studies, J. Meteor. Res, 28, p34-56. [https://doi.org/10.1007/s13351-014-3041-7]

	CMA	KMA	Meteo france	NCEP
System	BCC-CSM 1.2 (Beijing Climate Center Climate Prediction System version 1.2)	GloSea5 (Global Seasonal forecasting system version 5)	CNRM-CM 6.0 (Centre National de Recherches Meteorologiques)	CFSv2 (Climate Forecast System version 2)
Atmosphere	BCC_AGCM2.1 (Beijing Climate Center Atmospheric General Model version 2.1)	UM (Unified Model)	ARPEGE-Climat V6.1	GFS (Global Forecast System)
Ocean	GFDL MOM4 (Geophysical Fluid Dynamics Laboratory Modular Ocean Model version 4)	Global Ocean 5.0 (NEMO3.4)	NEMO3.2	GFDL MOM4
Sea ice	GFDL SIS (GFDL Sea Ice Simulator)	Global Sea Ice 6.0 (CICE4.1)	GELATO v5 (Global Experimental Leads and ice for Atmosphere and Ocean version 5)	GFDL SIS
Hindcast period	1994~2014	1991~2010	1993~2014	1999~2010
Hindcast frequency	Daily	4/month	2/month	Daily
Hindcast initial conditions	NCEP R1 (2.5^o × 2.5^o), BCC GODAS ocean initial conditions (1^o/3-1^o)	ERA Interim (0.75^o × 0.75^o), Seasonal ODA reanalysis	ERA interim (T255L60), MERCATOR-OCEAN ocean reanalyses (1^o × 1^o)	CFSR (Climate Forecast System Reanalysis) (T382)
Hindcast size	4	3	15	4
Reference	Wu et al. (2014)	MacLachlan et al. (2015)	Voldoire et al. (2013)	Saha et al. (2014)