원격상관을 이용한 동아시아 6월 강수의 예측

1. 서 론

동아시아 여름 몬순은 고유의 지형적 강제력으로 구별되는 아시아 기후 시스템의 구성요소 중 하나이다. 동아시아 여름 몬순은 유라시아 대륙과 태평양 간 거대한 열적 차이와 티베트 고원으로부터 많은 영향을 받으며, 열대 · 아열대 · 중위도 지역을 포함하는 복잡한 시공간적 구조를 가진다(Yanai et al., 1992; Li and Yanai, 1996; Chang et al., 2000; Wang et al., 2008).

또한 동아시아 여름 몬순은 태평양-동아시아 원격상관을 통해 엘니뇨-남방진동의 영향을 받는 것으로 알려져 있다. 로스비 파동과 해수면 온도 간의 상호작용은 북서태평양 고기압과 해수면 온도 편차를 유지시키고, 이는 엘니뇨-남방진동의 성숙단계부터 소멸단계까지 그 영향을 연장시켜 동아시아 몬순에 지연된 반응을 야기한다(Nitta, 1987; Lau, 1992; Wang and Fu, 2000).

동아시아 몬순 지역에서 수자원의 대부분은 여름 몬순에 의해 공급되기 때문에 여름철 강수의 예측이 매우 중요함에도 불구하고, 복잡한 구조로 인해 대부분의 역학모형들은 동아시아 몬순 지역의 강수를 적절하게 모의하지 못하고 있다.

Shukla (1998)는 특정 열대 지역의 계절 평균된 대기 특성은 전적으로 해수면 온도에 의해 결정된다고 설명하였다. 그러므로 해수면 온도를 앞서 또는 동시적으로 예측할 수 있다면, 대순환 모형을 이용하여 대기 특성을 예측하는 것이 가능하다. 또한 해수면 온도 변화가 충분히 크다면, 아열대 일부 지역의 계절 평균된 순환장 또한 예측이 가능하다.

MOS (Model Output Statistics)에서 회귀분석은 역학 모형 예측장을 회전, 크기 조정(scale), 수정하는 단순 선형 변형으로 생각될 수 있다. 회귀분석적 접근은 예측인자들과 예측변수를 과거 그들의 관계를 바탕으로 관련시키는 점에서 통계 예측 모형의 구축과 기본 맥락을 같이 한다(Glahn and Lowry, 1972; Mo and Strauss, 2002).

실제로 중위도 지역 계절 예측성의 한계를 극복하기 위하여 최근의 선행 연구들은 동아시아 여름철 강수를 직접 예측하는 방법 대신, 원격상관과 통계기법을 이용하여 간접적으로 예측함으로써 그 성능을 상당히 개선하였다(Kwon and Lee, 2014; Lee and Kwon, 2015). 그럼에도 불구하고 이러한 단순 선형회귀분석적 접근 방법은 계절 내 시간규모에서는 여전히 예측성의 한계를 가진다.

본 연구에서는 이전의 연구들이 여름철 평균된 계절 시간규모에서 북서태평양과 동아시아 간의 원격상관을 이해하고 강수 예측 성능을 개선한 것에서 더 나아가, 계절내 시간규모에서 동시 원격상관뿐만 아니라 유라시아와 동아시아 간의 지연된 원격상관을 바탕으로 추가적인 예측인자와 예측변수 간 관계를 규명하고 통계적으로 적합(fitting)된 예측모형의 성능을 검증하고자 하였다.

2. 자료 및 방법

역학 모형의 한계를 극복하기 위한 대안으로 통계적 기법을 활용하여 예측 성능을 개선하는 방안들이 많은 선행 연구들을 통해 제시되어 왔다(Barnett and Preisendorfer, 1987; Bretherton et al., 1992). Barnett and Preisendorfer (1987)는 예측변수의 분산을 가장 많이 설명하는 예측인자의 최적 선형 조합을 찾는 정준상관분석(Canonical Correlation Analysis, CCA)을 제안하였다. 정준상관 예측모형을 통해 예측인자가 특정한 분포를 가질 때 이와 관련된 예측변수의 기후 편차 분포를 산출하는 것이 가능하며, 이 때 예측인자와 예측변수는 다차원 벡터 정보를 가진다.

통계 모형 구성에는 다중 예측인자로 역학모형 GloSea5 (Global Seasonal Forecasting System version 5) 과거재현(hindcast) 실험의 850 hPa 바람 자료와 미 해양대기청(National Oceanic and Atmospheric Administration, NOAA) 기후 기록 자료(Climate Data Record, CDR)의 북반구 눈 덮임 자료 사용하였으며, 예측변수로 CMAP (CPC Merged Analysis of Precipitation) 월평균 자료를 사용하였다.

GloSea5는 영국 기상청이 개발한 전구 계절예측 시스템으로 2013년 7월부터 GloSea4를 대체하여 현업에 운용되고 있다. GloSea5는 앙상블 예측 시스템으로 대기, 해양, 해빙, 지면 과정이 포함된 대기-해양 결합 모형 HadGEM3의 고해상도 버전이다(MacLachlan et al., 2014). NOAA CDR은 과거의 육안 관측 기반 분석을 수치화하고 최신의 다중편광 원격탐사와 결합하여 생산된 반구 규모의 연속적인 자료이다. CMAP은 전구 강수를 우량계 관측값과 위성 기반 알고리즘으로부터의 추정값을 병합한 자료이다(Xie and Arkin, 1997).

GloSea5 자료의 수평 해상도는 경도 0.83도, 위도 0.56도, NOAA 자료는 경도 8도, 위도 2도, CMAP 자료는 경도 2.5도, 위도 2.5도 간격이다. 분석 기간은 기간이 가장 짧은 GloSea5 과거재현 자료를 기준으로 가용한 1996년부터 2009년까지 14년으로 일치시켰다. 모든 자료는 경향성과 기후 평균값이 제거된 편차 값을 사용하였다.

3. 동시 원격상관을 이용한 강수의 예측

북서태평양 몬순과 동아시아 몬순은 원격상관에 의해 서로 음의 상관관계를 가지며, 이는 북서태평양-동아시아 몬순 원격상관 또는 태평양-일본(Pacific-Japan, PJ) 원격상관으로 알려져 있다(Nitta, 1987; Lau et al., 2000). 여름철 북서태평양 지역의 대류활동이 강화(약화)되고 강수가 증가(감소)하면 로스비 파동의 전파에 의해 원격상관 패턴이 나타나고, 동아시아 지역에는 고기압성(저기압성) 흐름의 영향으로 강수량이 감소(증가)하게 된다(Wang et al., 2001, 2012).

Kwon and Lee (2014)와 동일한 방법으로 서로 다른 지역 변수들 간 결합 모드를 조합하는 정준상관 예측모형을 구성하였다. 예측인자는 GloSea5 3월 초기조건으로 적분된 과거재현 자료의 6월 북서태평양(100^o~160^oE, 5^o~30^oN) 지역 850 hPa 동서방향 바람편차를 사용하고, 예측변수는 동아시아(115^o~150^oE, 30^o~50^oN) 지역의 CMAP 6월 강수 편차를 사용하였다. 예측과정은 통계 기법을 기반으로 하면서 역학 모형의 예측장을 투입하여 계산되기 때문에 역학-통계 모형이라고도 한다. 예측변수(A_ik)와 예측인자(B_jk)는 특이 값 분해(Singular Value Decomposition, SVD)에 의해 다음과 같이 표현될 수 있다.

U_in와 V_jn은 정규화된 특이 벡터(singular vector)이고, p_nkt와 q_nk는 특이 값(singular value)의 시계열이다. i, j는 북서태평양 지역과 동아시아 지역의 격자 공간, k는 시간, n은 특이 값 분해 모드의 인덱스를 나타낸다.

B_jk1는 GloSea5로부터 예측된 특정 해 6월의 북서태평양 지역 850 hPa 동서방향 바람 편차이고, A_ik1는 예측모형으로부터 계산되는 같은 해 6월의 동아시아지역 강수량 편차이다. Figure 1a는 분석 기간 동안 GloSea5 과거재현 자료로부터의 6월 북서태평양 지역 850 hPa 동서방향 바람 편차와 CMAP 자료로부터의 6월 동아시아 지역 강수 편차 간의 첫 번째 SVD 모드를 보여준다. 예측모형에서 결합 모드는 5개까지 조합하였으며, 예측 성능 검증을 위해 1996년부터 2009년까지 개별 해 6월의 강수 편차를 예측하였다.

Fig. 1.

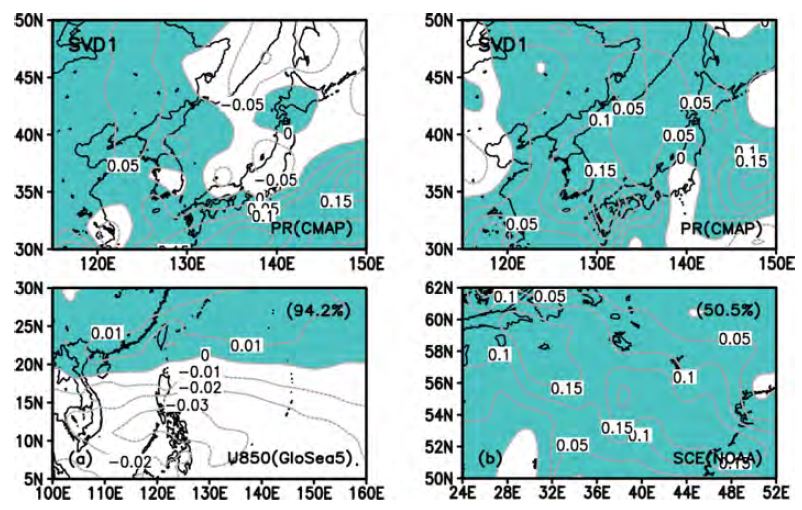
Leading SVD modes of (a) zonal wind anomalies (June) at 850 hPa over western North Pacific (5o~30oN, 100o~160oE) and snow cover extent anomalies (April) over (b) Eastern Europe (50o~62oN, 24o~52oE) with precipitation anomalies (June) over Northeast Asia for 1996~2009.

동시 원격상관을 바탕으로 구성된 예측모형을 이용하여 동아시아 지역 강수 편차를 예측한 결과 한반도를 포함한 대부분의 영역에서 상당 수준의 공간 패턴 예측 성능을 보이며, 동아시아 지역을 공간 평균한 강수 지수 또한 재분석 자료와 잘 일치하는 것으로 나타난다. 분석 기간 동안 예측모형이 예측한 동아시아 지역 강수 지수와 CMAP 강수 지수 간의 상관계수는 약 0.44로 나타나지만, 교차 검증된 예측 성능은 약 0.02으로 상당히 떨어진다. 이를 보완하기 위하여 다음 절에서는 추가적인 예측인자를 이용하는 또 다른 개별 정준상관 예측 모형을 적합한다.

4. 지연 원격상관을 이용한 강수의 예측

앞서 살펴본 북서태평양-동아시아 몬순 간 동시 원격상관뿐만 아니라, 북대서양-동아시아 또는 유라시아-동아시아 지역 간 지연 원격상관 관계가 존재하는 것으로 알려져 있다.

Yim et al. (2010)은 봄철 유라시아 지역 적설(snow cover) 이 동아시아 지역 여름철 대기 순환과 강수에 미치는 영향을 규명하였다. 주성분 분석을 통해 봄철 유라시아 적설 편차는 대륙(continent-wide) 패턴과 동서 쌍극(dipole) 패턴의 두 가지 구조로 특징지어지는데, 이 중 동서 쌍극 모드는 동아시아 여름 몬순 강수와 매우 밀접하게 관련되어 있다. 봄철 적설이 유라시아 서쪽과 동쪽에서 각각 양의 편차와 음의 편차를 가질 때, 이와 관련된 여름철 순환으로 500 hPa에서 양의 유라시아 패턴(동아시아 지역에 저기압성 편차)과 동아시아 지역 강수의 증가가 나타난다. 이는 봄철 유라시아 적설 패턴이 동아시아 여름철 몬순 강수의 잠재 예측인자가 될 수 있다는 것을 암시한다.

선행 연구에서 봄철(MAM) 평균된 유라시아 적설이 동아시아 여름철(JJA) 평균 강수에 미치는 영향을 규명한 것과 달리, 본 연구에서는 봄철 각 월별 유라시아 적설과 동아시아 6월 강수 간의 상관관계를 분석하여 서로 다른 지역의 3월과 4월 적설을 예측인자로 채택하였다. 3월 중국 북부 지역, 4월 유럽 동부 지역의 적설과 6월 동아시아 지역 강수 간의 상관계수는 각각 −0.61과 0.59로 높은 상관관계를 보이는 것을 확인하였다(Fig. 2).

Fig. 2.

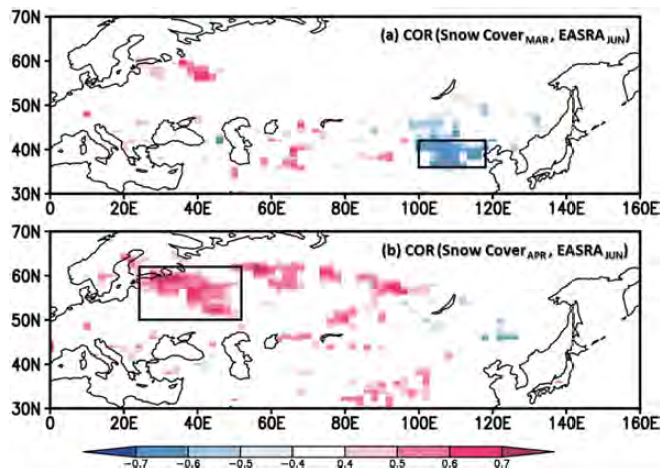
Maps of correlated snow cover extent anomalies for (a) March and (b) April onto June precipitation anomalies averaged over the Northeast Asia (30o~50oN, 115o~150oE) for 1996~2009.

중국 북부 및 유럽 동부 지역 적설과의 원격상관은 선행 연구의 주성분 분석 결과 상위모드에서 나타나는 쌍극 패턴과 어느 정도 공간적으로 일치한다. 이를 바탕으로 앞 절의 동시 원격상관을 이용한 예측모형과 동일한 방법으로 정준상관 예측모형을 구성하였다.

예측인자는 3월 중국 북부(100^o~120^oE, 36^o~42^oN) 지역과 4월 유럽 동부(24^o~52^oE, 50^o~62^oN) 지역의 NOAA 적설 편차를 사용하고, 예측변수는 동아시아(115^o~150^oE, 30^o~50^oN) 지역의 CMAP 6월 강수 편차를 사용하였다. 3장과 달리 식에서 B_jk1는 각각 3월 중국 북부 지역과 4월 유럽 동부 지역 NOAA 적설 자료이고, A_ik1는 예측모형으로부터 계산되는 동아시아 지역 6월 강수 편차이다. Figure 1b는 분석 기간 동안 NOAA의 유럽 동부 지역 4월 적설 편차와 CMAP의 동아시아 지역 6월 강수 편차 간의 첫 번째 SVD 모드를 보여준다. 예측모형에서 결합 모드는 이전과 동일하게 5개까지 조합하였다.

지연 원격상관을 바탕으로 구성된 예측모형을 이용하여 동아시아 지역 강수 편차를 예측한 결과 또한 한반도를 포함하는 중위도(35^o~45^oN) 영역을 중심으로 상당한 수준의 공간 패턴 예측 성능을 보이며, 동아시아 지역을 공간 평균한 강수 지수 또한 재분석 자료와 잘 일치하는 것으로 나타난다. 분석 기간 동안 예측모형이 예측한 동아시아 지역 강수 지수와 CMAP 강수 지수 간의 상관계수는 약 0.79, 교차 검증된 성능은 약 0.55로 나타난다.

5. 앙상블 정준상관을 이용한 강수의 예측

정준상관은 경험적 통계 접근 방법으로 예측인자와 예측변수 간의 공변성(covariability)을 바탕으로 예측 결과를 생산하는데, 보다 확장된 앙상블 정준상관(Ensemble Canonical Correlation, ECC)은 예측인자와 예측변수가 1 : 1로 적합된 개별 정준상관 예측모형들의 평균이 실제 기후 시스템과 중첩되는 영역을 최대화하는 것을 그 목적으로 한다. 앙상블 정준상관에서 예측인자의 수에는 제한이 없으며, 고유벡터 분석과 달리 예측인자들 간 직교(orthogonality)의 제약으로부터 자유로운 것이 장점이다(Lau et al., 2002).

복수의 예측인자들을 하나의 자료로 무차원(dimensionless) 시계열화하여 정준상관 분석을 수행하면 개별 예측인자와 예측변수 간의 고유 결합모드에 간섭이 발생하여 예측 성능이 개선되지 않거나 오히려 다소 떨어지는 결과를 나타낸다. 이와 달리 개별 예측인자와 예측변수가 1 : 1로 적합된 예측모형들의 계산 결과를 평균하는 앙상블 정준상관 예측을 통해 예측 성능뿐만 아니라 교차검증 성능 또한 크게 향상시킬 수 있다(Fig. 3).

앙상블 정준상관을 이용하면 동시 원격상관 기반 예측모형과 지연 원격상관 기반 예측모형을 이용한 각각의 예측보다 정량적으로 개선된 예측 결과를 얻을 수 있다(Fig. 4). 분석 기간 동안 앙상블 정준상관 예측모형이 예측한 동아시아 지역 강수 지수와 CMAP 강수 지수 간의 상관계수는 약 0.85, 교차 검증된 성능은 약 0.54로 나타난다.

Fig. 3.

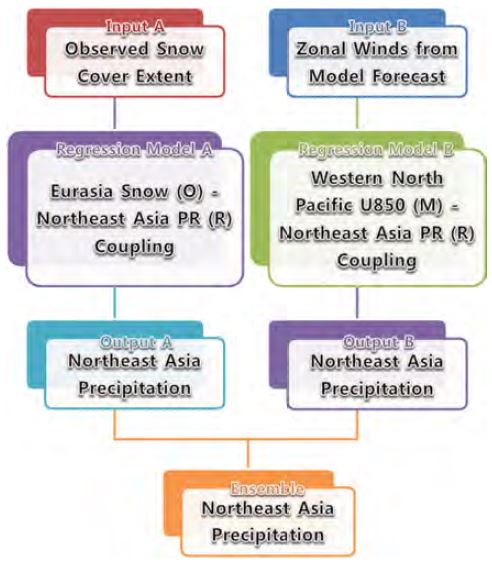
Schematic diagram of ensemble canonical correlation forecast for subseasonal precipitation over the Northeast Asia (O: observation, M: model, R: reanalysis).

Fig. 4.

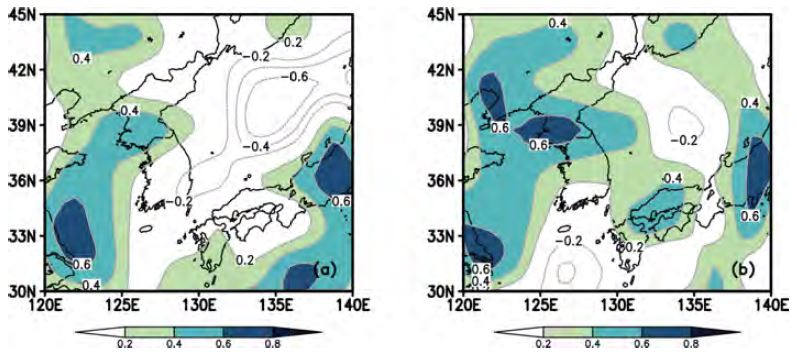
Maps of temporal correlation coefficients of monthly (June) precipitation anomalies from (a) single CCA forecast and (b) ensemble CCA forecast with those from CMAP over the Northeast Asia (30o~50oN, 115o~150oE) for 1996~2009.

또한 동시 원격상관 예측모형에 투입되는 역학모형 예측장과 지연 원격상관 예측모형에 투입되는 관측자료를 모두 예측인자로 활용하게 되기 때문에, 역학모형의 예측장만을 사용하여 예측모형을 구성하였을 때 발생할 수 있는 불확실성을 줄이고 예측모형의 안정성을 상당 부분 향상시킬 수 있다.

6. 결론 및 토의

동아시아 지역의 여름철 강수는 몬순과 관련된 극한 기상 및 기후 현상으로 세계 인구의 약 1/3에 달하는 이 지역 인구에 미치는 사회 · 경제적 영향이 크기 때문에, 이를 정확하게 예측하는 것이 매우 중요하다. 그럼에도 불구하고 현재 수준의 역학모형들은 동아시아 지역을 포함하는 중위도 지역의 강수뿐만 아니라 이와 관련된 원격상관을 모의하는 데 여전히 한계가 있다.

본 연구에서는 이러한 역학모형의 한계를 극복하기 위한 대안으로 통계적 기법 중 하나인 정준상관 모형을 구성하고, 지연 상관관계 기반의 적설 관측자료와 동시 상관관계 기반의 하층 바람 역학모형 예측자료를 각각 예측인자로 투입하여 예측 성능을 개선하였다. 또한 개별 적합된 정준상관 모형으로부터 계산된 예측 결과를 평균하는 앙상블 정준상관 기법을 이용함으로써, 역학모형 예측자료만을 예측 인자로 사용하여 구성된 단일 정준상관 모형의 잠재 불확실성을 줄이고 예측모형의 안정성을 향상시켰다.

그럼에도 불구하고 예측모형 적합에 사용된 자료의 기간이 충분히 길지 않다는 점은 통계 이론을 기반으로 하는 예측모형이라는 측면에서 여전히 해결해야 할 부분으로 남아 있다. 하지만 기존 GloSea5-GA3에서 역학코어와 물리과정이 개선된 GloSea5-GC2의 과거재현 실험의 경우 1991년부터 2010년까지 약 20년 동안 이전보다 장기간의 자료를 제공하고 있기 때문에, 이를 적용하여 예측모형을 적합한다면 적은 표본으로 인한 불안정성 또한 어느 정도 해소할 수 있을 것으로 생각된다.

Acknowledgments

본 논문의 개선을 위해 좋은 의견을 제시해 주신 심사위원께 감사를 드립니다. 이 연구는 한국기상산업진흥원(KMIPA 2015-2111)의 지원으로 수행되었습니다.

References

• Barnett, T. P., and R. Preisendorfer, (1987), Origins and levels of monthly and seasonal forecast skill for United States surface air temperatures determined by canonical correlation analysis, Mon. Wea. Rev., 115, p1825-1850. [https://doi.org/10.1175/1520-0493(1987)115<1825:OALOMA>2.0.CO;2]
• Bretherton, C. S., C. Smith, and J. M. Wallace, (1992), An intercomparison of methods for finding coupled patterns in climate data, J. Climate, 5, p541-560. [https://doi.org/10.1175/1520-0442(1992)005<0541:AIOMFF>2.0.CO;2]
• Chang, C. P., Y. Zhang, and T. Li, (2000), Interannual and interdecadal variations of the East Asian summer monsoon and tropical SSTs. Part I: Role of the subtropical ridge, J. Climate, 13, p4310-4325. [https://doi.org/10.1175/1520-0442(2000)013<4310:IAIVOT>2.0.CO;2]
• Glahn, H. R., and D. A. Lowry, (1972), The use of model output statistics (MOS) in objective weather forecasting, J. Appl. Meteorl., 11, p1203-1211. [https://doi.org/10.1175/1520-0450(1972)011<1203:TUOMOS>2.0.CO;2]
• Kwon, M., and K.-J. Lee, (2014), A prediction of Northeast Asian summer precipitation using the NCEP Climate Forecast System and canonical correlation analysis, J. Korean Earth Sci. Soc., 35, p88-94, (in Korean with English abstract). [https://doi.org/10.5467/JKESS.2014.35.1.88]
• Lau, K.-M., (1992), The East Asian summer monsoon rainfall variability and climate teleconnection, J. Meteor. Soc. Japan, 70, p211-242.
• Lau, K.-M., K.-M. Kim, and S. Yang, (2000), Dynamical and boundary forcing characteristics of regional components of the Asian summer monsoon, J. Climate, 13, p2461-2482. [https://doi.org/10.1175/1520-0442(2000)013<2461:DABFCO>2.0.CO;2]
• Lau, K.-M., K.-M. Kim, and S. S. P. Shen, (2002), Potential predictability of seasonal precipitation over the United States from canonical ensemble correlation predictions, Geophys. Res. Lett., 29, p1-4. [https://doi.org/10.1029/2001GL014263]
• Lee, K.-J., and M. Kwon, (2015), A prediction of Northeast Asian summer precipitation using teleconnection, Atmosphere, 25, p179-183, (in Korean with English abstract). [https://doi.org/10.14191/Atmos.2015.25.1.179]
• Li, C., and M. Yanai, (1996), The onset and interannual variability of the Asian summer monsoon in relation to land-sea thermal contrast, J. Climate, 9, p358-375. [https://doi.org/10.1175/1520-0442(1996)009<0358:TOAIVO>2.0.CO;2]
• MacLachlan, C., and Coauthors , (2014), Global Seasonal forecast system version 5 (GloSea5): a high-resolution seasonal forecast system, Quart. J. Roy. Meteor. Soc., 141, p1072-1084. [https://doi.org/10.1002/qj.2396]
• Mo, R., and D. M. Strauss, (2002), Statistical-dynamical seasonal prediction based on principal component regression of GCM ensemble integrations, Mon. Wea. Rev., 130, p2167-2187. [https://doi.org/10.1175/1520-0493(2002)130<2167:SDSPBO>2.0.CO;2]
• Nitta, T., (1987), Convective activities in the tropical western Pacific and their impact on the Northern Hemisphere summer circulation, J. Meteor. Soc. Japan, 65, p373-390.
• Shukla, J., (1998), Predictability in the midst of chaos: A scientific basis for climate forecasting, Science, 282, p728-731. [https://doi.org/10.1126/science.282.5389.728]
• Wang, B., and X. Fu, (2000), Pacific-East Asian teleconnection: How does ENSO affect East Asian climate?, J. Climate, 13, p1517-1536. [https://doi.org/10.1175/1520-0442(2000)013<1517:PEATHD>2.0.CO;2]
• Wang, B., R. Wu, and K.-M. Lau, (2001), Interannual variability of the Asian summer monsoon: Contrasts between the Indian and the western North Pacific-East Asian monsoons, J. Climate, 14, p4073-4090. [https://doi.org/10.1175/1520-0442(2001)014<4073:IVOTAS>2.0.CO;2]
• Wang, B., Z. Wu, J. Li, J. Liu, C.-P. Chang, Y. Ding, and G. Wu, (2008), How to measure the strength of the East Asian summer monsoon, J. Climate, 21, p4449-4463. [https://doi.org/10.1175/2008JCLI2183.1]
• Wang, B., B. Xiang, and J.-Y. Lee, (2012), Subtropical high predictability establishes a promising way for monsoon and tropical storm predictions, Proc. Natl. Acad. Sci., 110, p2718-2722. [https://doi.org/10.1073/pnas.1214626110]
• Wilks, D. S., (1995), Statistical Methods in the Atmospheric Sciences, Academic Press, p220-226.
• Xie, P., and A. Arkin, (1997), Global precipitation: A 17- year monthly analysis based on gauge observations, satellite estimates, and numerical model outputs, Bull. Amer. Meteor. Soc., 78, p2539-2558. [https://doi.org/10.1175/1520-0477(1997)078<2539:GPAYMA>2.0.CO;2]
• Yanai, M., C. Li, and Z. Song, (1992), Seasonal heating of the Tibetan Plateau and its effects on the evolution of the Asian summer monsoon, J. Meteor. Soc. Japan, 70, p319-351.
• Yim, S.-Y., J.-G. Jhun, R. Lu, and B. Wang, (2010), Two distinct patterns of spring Eurasian snow cover anomaly and their impacts on the East Asian summer monsoon, J. Geophys. Res., 115, pD22113. [https://doi.org/10.1029/2010jd013996]