[ Technical Note ]

Atmosphere - Vol. 26, No. 4, pp.697-709

ISSN: 1598-3560 (Print) 2288-3266 (Online)

Print publication date Dec 2016

Received 27 Sep 2016 Revised 18 Oct 2016 Accepted 25 Oct 2016

DOI: https://doi.org/10.14191/Atmos.2016.26.4.697

PRISM과 GEV 방법을 활용한 30 m 해상도의 격자형 기온 극값 추정 방법 연구

이준리 ; 안중배^* ; 정하규

부산대학교 지구환경시스템학부

A Study on the Method for Estimating the 30 m-Resolution Daily Temperature Extreme Value Using PRISM and GEV Method

Joonlee Lee ; Joong-Bae Ahn^* ; Ha-Gyu Jeong

Division of Earth Environmental System, Pusan National University, Busan, Korea

Correspondence to: ^* Joong-Bae Ahn, Division of Earth Environmental System, Pusan National University, Busandaehak-ro 63 beon-gil 2, Geumjeong-gu, Busan 46241, Korea. Phone: +82-51-514-1932, Fax: +82-51-514-1932 E-mail: jbahn@pusan.ac.kr

Abstract

This study estimates and evaluates the extreme value of 30 m-resolution daily maximum and minimum temperatures over South Korea, using inverse distance weighting (IDW), parameter-elevation regression on independent slopes model (PRISM) and generalized extreme value (GEV) method. The three experiments are designed and performed to find the optimal estimation strategy to obtain extreme value. First experiment (EXP1) applies GEV firstly to automated surface observing system (ASOS) to estimate extreme value and then applies IDW to produce high-resolution extreme values. Second experiment (EXP2) is same as EXP1, but using PRISM to make the high-resolution extreme value instead of IDW. Third experiment (EXP3) firstly applies PRISM to ASOS to produce the high-resolution temperature field, and then applies GEV method to make high resolution extreme value data. By comparing these 3 experiments with extreme values obtained from observation data, we find that EXP3 shows the best performance to estimate extreme values of maximum and minimum temperatures, followed by EXP1 and EXP2. It is revealed that EXP1 and EXP2 have a limitation to estimate the extreme value at each grid point correctly because the extreme values of these experiments with 30 m-resolution are calculated from only 60 extreme values obtained from ASOS. On the other hand, the extreme value of EXP3 is similar to observation compared to others, since EXP3 produces 30m-resolution daily temperature through PRISM, and then applies GEV to that result at each grid point. This result indicates that the quality of statistically produced high-resolution extreme values which are estimated from observation data is different depending on the combination and procedure order of statistical methods.

Keywords:

PRISM, IDW, GEV, extreme value, high-resolution, daily minimum and maximum temperature

1. 서 론

산업혁명 이후 이산화탄소를 포함한 온실가스의 증가로 지구 온난화가 진행되고 있다. 기후변화에 관한 정부 간 협의체(Intergovernmental Panel on Climate Change, IPCC)의 2013년 보고서에 의하면 지난 133년간(1880~2012년) 지구 평균 기온이 약 0.85℃ 상승하였으며, 최근 30년(1983~2012년) 동안 지구의 평균기온은 1850년 이래 가장 더웠던 것으로 발표하였다. 이러한 기온 증가는 폭염, 가뭄, 집중호우 등 기상 이변의 발생 빈도와 강도를 증가시켜서, 농업 및 인문 · 사회 분야 등 전반적인 인간활동에 영향을 준다. 최근 한반도의 경우, 태풍, 폭우, 폭염 등과 같은 이상기상의 발생빈도가 2008년도에서는 1회, 2010년도에는 5회, 2011년도에선 11회로 매년 증가함에 따라 기상재해도 빈번히 발생하고 있으며, 농업 기상재해 복구비 역시 2008년에는 약 921억원에서 2011년에는 4413억으로 약 5배 급증하였다. 이 같은 변화는 곡물가격의 변동 및 식량 위기에 의한 사회적 불안과 경제 공황을 야기할 수 있다. 그렇기 때문에 기온 증가로 인해 야기되는 기상 이변 등과 같은 극한 기후현상 연구의 중요성이 많은 선행 연구들에서 강조되고 있다(e.g., IPCC, 2013).

상세한 기상자료의 극한값(extreme value)을 생산하기 위해서는 고해상도 기상정보가 필요하다. 최근 농업을 포함한 공학, 수문, 경제 등 다양한 분야에서도 고해상도 격자 기상정보의 활용성과 중요성이 증대되고 있다(Ahn et al., 2014). 그럼에도 불구하고, 관측된 자료로부터 고르게 분포된 고해상도 기상정보를 얻는 것은 쉽지 않다. 70% 이상이 산으로 이루어진 우리나라의 경우, 다른 나라에 비해 조밀한 관측망이 구축되어 있다고 하더라도 대부분의 관측소들이 유지 보수 등의 문제로 300 m 이하의 낮은 고도에 위치하거나 대도시에 편중되어 있다(e.g., Ahn et al., 2012). 이러한 공간적 제약을 극복하기 위해서 여러 가지 통계적 방안을 이용한 보간법(interpolation)이 주로 사용된다. 통계적 방법에는 거리를 고려하지 않고 단지 통계적 · 물리적 관계에만 의존하는 선형 · 비선형 회귀(Schoof and Pryor, 2001) 방법과 거리만의 함수로 계산하는 Barnes 기법(Barnes, 1964), Cressman 기법(Cressman, 1959), 역거리 가중법(Inverse Distance Weighting, IDW) (Szolgay et al., 2009), 거리뿐만 아니라 지형학적 특성까지 고려하는 PRISM (Parameter-elevation Regressions on Independent Slope Model)(e.g., Daly et al., 1994; Ahn et al., 2014) 등이 있다. 여기서 PRISM은 다른 통계적 기법과 비교하여 인접한 기상자료에 대한 의존성이 상대적으로 작고, 지리적 특성을 비교적 잘 반영하여, 고르게 분포되지 않은 관측자료로부터 고분해능 격자정보를 추정할 때 유용하게 사용 가능하다. Hong et al. (2007)은 남한에 대해 최적화된 K-PRISM을 제시하였으며, 이를 이용하여 5 km 해상도의 기온 격자자료를 생산하였다. 그리고 Kim et al. (2012; 2013)에서는 MK (Modified Korean)-PRISM 기법을 개발하여 1 km 해상도의 격자형 일 기상자료를 생산하였으며, Ahn et al. (2014)에서도 일별 기온자료에 최적화된 PRISM을 개발하여 30 m 해상도의 일별 기온자료를 생산 및 검증하였다.

100 m 이상의 해상도에서는 빌딩 주변과 경작지 경계에서 발생하는 국지기상 변화를 살펴보기 힘들다(Rider et al., 1963). 특히 2015년 우리나라의 가구원 1인당 평균 경지면적이 약 74.5 m × 74.5 m임을 고려할 때, 우리나라 농경지에서 발생하는 병해충 및 작물 생육 환경과 관련된 국지 기상을 살펴보기 위해서는 100 m 이하의 고해상도 기상 정보가 필요하다. 따라서 본 연구에서는 통계기법들을 이용하여 남한영역에 대한 30 m 고해상도 격자형 극한값을 산출하고자 하였다. 평균적인 하층 난류의 크기를 고려한 30 m 정도의 기후정보는 국지기상의 특성을 표현하기 때문에(Rider et al., 1963), 농업 등 다양한 분야로의 활용도가 높을 것으로 예상된다(Ahn et al., 2014). 극한값을 추정하는 방법으로는 일반화 극단 분포(Generalized Extreme Value Distribution, GEV) 방법을 사용하였으며, 30 m 해상도를 추정하기 위해서는 IDW와 PRISM을 이용하였다. 통계적 방법들에 대한 자세한 설명은 2.2장에서 언급하였다. 본 연구는 IDW, PRISM, GEV와 같은 통계적 방법들의 조합을 통해 최적의 극한값을 추정하는데 초점을 두었다.

2. 자료 및 방법

2.1 자료

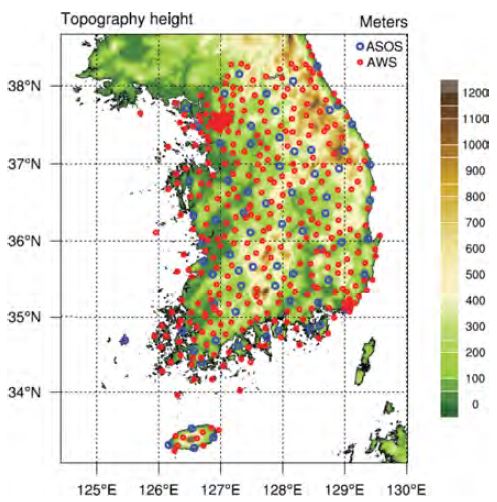
본 연구에서는 IDW와 PRISM의 입력자료 및 검증 자료로 1999년부터 2013년까지 기상청에서 관측한 기온자료를 사용하였다. 기상청 관측자료는 지상 기상관측(Automated Surface Observing System, ASOS) 지점들에서 관측된 자료와 자동기상관측지점(Automated Weather Station, AWS)에서 관측된 자료로 나뉜다. 본 연구에서는 IDW와 PRISM의 입력자료로 60개의 ASOS를 사용하였으며, 검증자료로는 320개의 AWS를 사용하였다. AWS의 경우 1990년 후반부터 구축되었기 때문에 30년 이상의 기후값을 생산하는데 적합하지 않아 IDW와 PRISM의 입력자료는 1973년부터 관측이 시작된 60개의 ASOS 자료만을 사용하였으며, AWS는 IDW와 PRISM을 통해 상세화된 자료의 검증에 사용되었다. 검증기간은 AWS 자료간의 동질성을 고려하여 1999년부터 2013년 총 15년 동안 관측값이 있는 320개의 AWS 지점을 사용하였다. IDW와 PRISM의 입력자료로 사용된 ASOS와 검증에 사용된 AWS의 위치 정보는 Fig. 1에 파란색과 빨간색 동그라미로 각각 나타내었다. 고해상도 격자형 지형자료는 30 m 해상도의 ASTER Global Digital Elevation Map(GDEM) (Frey and Paul, 2012) 자료를 사용하였으며(Fig. 1), 이 자료를 이용하여 PRISM의 입력자료로 필요한 지향면(topographic facet)과 해양도(coastal proximity) 정보도 산출하였다(Ahn et al., 2014).

Fig. 1.

1. Locations of ASOS and AWS in South Korea (height Unit: m).

2.2 방법

2.2.1 역거리 가중법(Inverse Distance Weighting, IDW)

역거리 가중법(IDW)은 기상요소의 동질성을 거리만의 함수로 계산하는 보간법(interpolation)으로, 이미 알고 있는 관측의 위치 정보를 이용하여 보간점의 거리에 반비례하게 가중치를 두어 보간점의 값을 계산하는 방법이다(e.g., Szolgay et al., 2009; Ahn et al., 2014). IDW 방법은 다음과 같다.

T = ∑ i = 1 n T s i W i / ∑ i = 1 n W i W i = 1 d i 2

여기서 T는 추정하고자 하는 특정 격자점의 기온이며, T_s는 특정 격자점을 중심으로 영향반경 안에 포함된 n개의 관측점 중에서 i번째 관측점의 기온을 의미한다. 여기에서 영향반경은 극한값의 국지성을 표현함에 있어서 매우 중요한 요소이다. 만약 영향반경이 작으면 관측지점이 반영되지 않는 영역이 존재하게 되고, 반대로 영향반경이 너무 크면 많은 관측지점이 영향을 주어 국지적인 효과가 나타나지 않는다. 본 연구에서는 입력자료로 사용되는 60개의 ASOS의 관측 지점 사이의 최소거리가 13.7 km에서 최대 거리가 144.6 km 인 것을 고려하여, 선행연구와 같이 IDW의 영향반경으로 100 km를 이용하였다(Ahn et al., 2014). W_i는 i번째 관측점의 가중치를 의미하며, d_i는 특정 격자점과 i번째 관측지점과의 거리를 의미한다. 이때 각 관측지점의 가중치(W_i)는 거리의 제곱에 반비례로 계산된다.

2.2.2 PRISM (Parameter-elevation Regression on Independent Slopes Model)

PRISM은 거리, 고도, 지향면, 해양도 등의 지형학적 특성과 기상인자 사이의 관계식을 이용하여 고해상도 격자형 기상자료를 생산하는 방법이다(e.g., Daly et al., 1994). 이 방법은 단순히 거리뿐만 아니라 다른 통계적 방법들이 표현할 수 없었던 지형학적 특성을 반영할 수 있다는 장점이 있다. 본 연구에서 수행된 PRISM 기법은 Ahn et al. (2014)에서 사용했던 방법으로, 남한 기후에 적합하게 개발된 K-PRISM에서(Hong et al., 2007) 일부 요소를 개선하여 만들어진 방법이다. 개선된 요소를 간략히 설명하면, 이 방법은 30 m의 격자 간격과 일 단위의 시간 간격에 적합하도록 각 격자점의 기온 추정에 사용되는 가중 회귀식의 기울기를 관측 자료로부터 계산된 일 평균 기온감율로 이용하였으며, ± 0.5 표준편차로 최고 · 최저값을 제한함으로써 비현실적으로 추정되는 값을 방지하였다. 그리고 지향면의 경사 방향을 8 방위로 구분하는 기존의 연구에서 16 방위로 더욱 세분화하여 보다 현실과 유사한 고해상도 격자형 기상자료를 생산하였다. PRISM에 대한 보다 상세한 정보는 Ahn et al. (2014)의 문헌을 참고하기 바란다. 비록 이 논문에서는 1월 기온에 대해서만 PRISM의 타당성을 검증했지만, PRISM의 가중치는 각 격자점의 영향반경 내에 속한 관측지점의 값과 고도자료를 이용하여 추정되므로 계절에 상관없이 사용이 가능하다(e.g., Hong et al., 2007; Kim et al., 2012).

2.2.3 일반화 극단 분포(Generalized Extreme Value, GEV) 방법

본 연구에서는 기온의 극한값을 추정하기 위해 GEV 방법을 사용하였다. 여기서 사용한 GEV 방법은 Gumbel, Frechet, Weibull 과 같이 3가지 타입의 극한값 분포를 결합하여 일반화 시킨 것으로, Fisher and Tippett (1928)를 포함하여 많은 선행연구에서 극한값을 추정하는 방법으로 사용된다(e.g., Park and Jung, 2002; Im et al., 2015; Ahn et al., 2016). GEV 방법의 식은 다음과 같다.

G x; μ, σ, ξ = exp - ξ x - μ σ - 1 ξ

여기서 μ는 위치모수(location parameter), σ는 척도 모수(scale parameter), ξ는 형상모수(shape parameter)이다. 이처럼 GEV 방법은 3가지의 모수들(parameters)을 이용하여 극한값 분포를 추정하기 때문에, 정확한 극한값을 얻기 위해서는 주어진 정보에서 3가지 모수들을 잘 추정해야만 한다. 본 연구에서 3가지 모수들을 추정하기 위해 사용한 방법은 L-moments 방법이다(Hosking, 1990). 이 방법은 일반적으로 많이 사용되는 최대우도법(Maximum likelihood)에 비해 작은 표본(sample size)에서도 좋은 결과를 보인다(e.g., Im et al., 2015). 본 연구에서는 15년(1999~2013)기간에 대해 추정된 기온의 극한값 분포에서 5년, 10년, 20년, 30년 재현주기로 발생할 수 있는 극한값을 추정하였다.

3. 실험설계

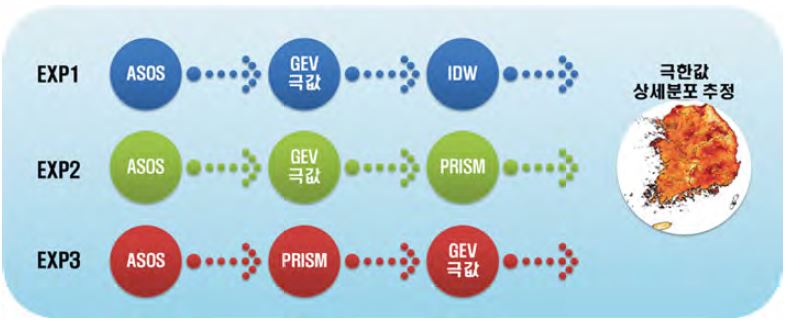
일반적으로 관측지점에서의 극한값은 GEV와 같은 통계적 기법을 통해 정확하게 추정이 가능하지만 관측이 되지 않는 지역에서의 극한값은 추정이 상대적으로 어렵다. 특히, 30 m 격자 간격의 고해상도 기온 극한값을 정확하게 추정하기 위해서는 관측이 되지 않는 지점의 기온을 보다 정확하게 추정할 수 있어야 한다. 즉, 고해상도의 기온자료를 생산하는 방법과 극한값을 추정하는 방법에 따라 최종적으로 생산되는 극한값이 달라지게 된다. 이에 본 연구에서는 30 m 해상도의 격자형 기온 극한값을 보다 정확하게 생산하는 방법을 살펴보기 위해서, Fig. 2와 같이 3가지 방법의 실험을 수행하였다. EXP1은 60개 지점의 ASOS에서 극한값을 추정한 후, 추정된 극한값에 IDW를 사용하여 30 m 해상도의 격자형 기온 극한값을 생산하는 실험이다. 그리고 EXP2는 IDW 대신 PRISM을 사용하여 고해상도 격자형 기온 극한값을 생산하는 실험이다. 이 실험들은 관측지점에서 정확한 기온의 극한값을 구한 후, 거리만을 고려하는 IDW와 거리, 고도, 지향면, 해양도 등의 지형학적 특성을 고려하는 PRISM을 사용하여 상세한 극한값 분포를 만드는 것이다. 반면, EXP3는 ASOS 자료에서 PRISM을 통해 고해상도 기온 분포를 만들고, 각 격자점마다 GEV를 적용하여 극한값을 추정하는 실험이다. 이 실험은 고해상도 기온 분포를 생산한 후, 각 격자점마다 기온의 극한값을 구하기 때문에 보다 현실적인 기온 극한값이 생산될 것으로 기대되나 다른 실험들에 비해 대략 600만배 많은 계산량을 필요로 한다.

Fig. 2.

Schematic diagram for the three experiments to estimate fine-resolution distribution of temperature extreme values.

4. 결 과

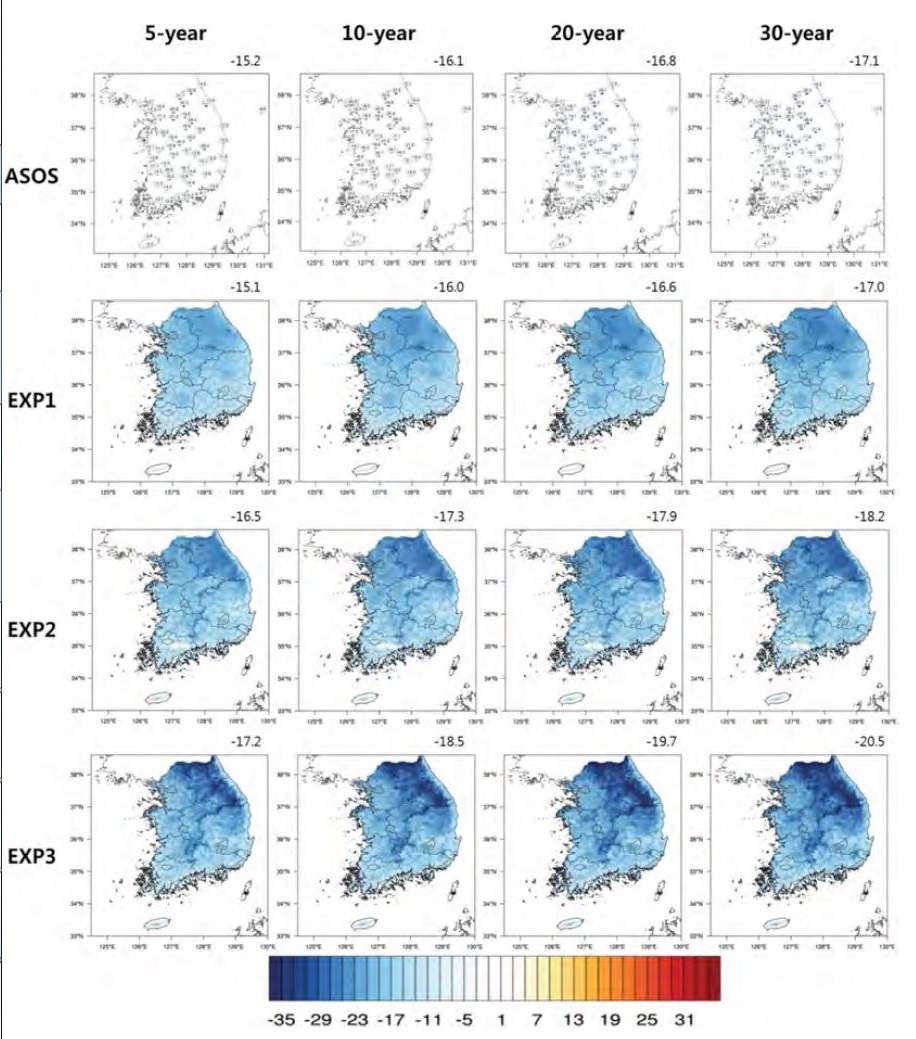
본 연구에서는 고해상도의 격자자료를 생산하는 방법과 극한값을 추정하는 순서에 따라 30 m 해상도의 격자형 기온 극한값의 분포의 차이를 살펴보기 위해 ASOS 및 각 실험으로부터 추정한 5년, 10년, 20년, 30년 재현주기로 발생할 수 있는 남한의 최고기온과 최저기온 극한값 분포를 Figs. 3과 4에 나타내었다. 여기서 ASOS는 EXP1의 IDW와 EXP2에서 PRISM의 입력자료로 사용되기 때문에 각 실험과 비교 하기 위해 ASOS의 극한값 분포도 함께 나타내었다. 또한, 각 실험에서 추정된 극한값의 신뢰도를 살펴보기 위해 60개 지점의 ASOS와 320개 지점의 AWS 자료들을 합친 좀 더 조밀한 관측자료(이하 ASOS + AWS)들의 각 재현주기 별 추정된 최고 · 최저기온의 극한값 및 99% 신뢰구간을 Fig. 5에 나타내었다. 극한값 공간분포를 그린 Figs. 3과 4의 오른쪽 상단의 값은 남한영역에 면적평균값을 의미한다. 먼저 최고기온의 경우, 5년, 10년, 20년, 30년과 같이 재현주기가 길어짐에 따라 ASOS를 포함한 모든 실험들의 최고 기온의 극한값도 점차 증가함을 보였다(Fig. 3). 하지만 각 실험 방법에 따라 각 재현주기에 대한 극한값이 변하는 정도는 IDW와 PRISM의 입력자료로 사용된 ASOS와 차이가 있었다. EXP1의 경우, 남한 영역의 면적평균값이 모든 재현주기에서 ASOS와 유사하게 나타났으며(Fig. 3), ASOS + AWS 에서 추정된 최고기온의 극한값과 비교해 보아도, EXP1의 영역평균값들이 모든 재현주기에서 99% 신뢰구간 내에 유의하였다(Fig. 5a). 그러나 공간적 분포를 살펴보면, EXP1은 ASOS에서 극한값을 추정한 후, 거리만을 고려하는 IDW를 적용하여 고해상도 격자형 기온 극한값을 추정했기 때문에 지형적 효과가 고려되지 않았다. 즉, 30 m 고해상도 자료임에도 불구하고 남한의 동쪽부근에 위치한 태백산맥과 소백산맥 등 해발고도가 높은 지역에 동그라미 형태의 분포가 나타날 뿐 상세한 극한값 분포가 나타나지 않았다. 이는 EXP1에서 추정된 극한값의 영역평균은 관측과 유사할지라도, 상세한 극한값 공간분포는 나타내지 못함을 의미한다. 반면 EXP2는 ASOS에서 극한값을 추정한 후, 다양한 지형적 요소를 반영하는 PRISM을 적용하였기 때문에 최종적으로 추정된 극한값 분포에서 상세한 지형이 나타났다. 하지만 면적평균값을 살펴보면, ASOS에 비해 전반적인 최고기온 극한값이 낮게 추정되고 있다. ASOS+AWS에서 추정된 최고기온의 극한값과 비교해 보면(Fig. 5a), 5년과 10년 재현주기에서는 EXP2의 극한값이 관측에 비해 낮게 추정되어서 99% 신뢰구간에 유의하지 못했으며, 20년, 30년 재현주기에서는 99% 신뢰구간에 유의하였다. 이러한 결과는 각 격자점마다 최고기온의 극한값을 추정하지 않고 60개의 ASOS 지점에서 추정된 극한값을 PRSIM에 적용했기 때문에 발생되는 문제이다. 이러한 문제는 PRSIM을 적용한 후, 각 격자점마다 최고기온의 극한값을 추정한 EXP3에서 해소되었다. EXP1과 비교했을 때, EXP3의 면적평균값은 유사하게 나타났지만, 공간적 분포에서는 EXP1과 전혀 다르게 상세한 지형이 반영되는 결과를 보였다. 관측과 비교해 보았을 때도 극한값 공간분포가 상세한 지형을 반영함과 동시에 남한영역에 대해 ASOS와 유사한 면적평균값을 나타내었다. ASOS + AWS에서 추정된 최고기온의 극한값과 비교해 보아도, EXP3의 영역평균값들이 모든 재현주기에서 99% 신뢰구간 내에 유의하였다(Fig. 5a).

Fig. 3.

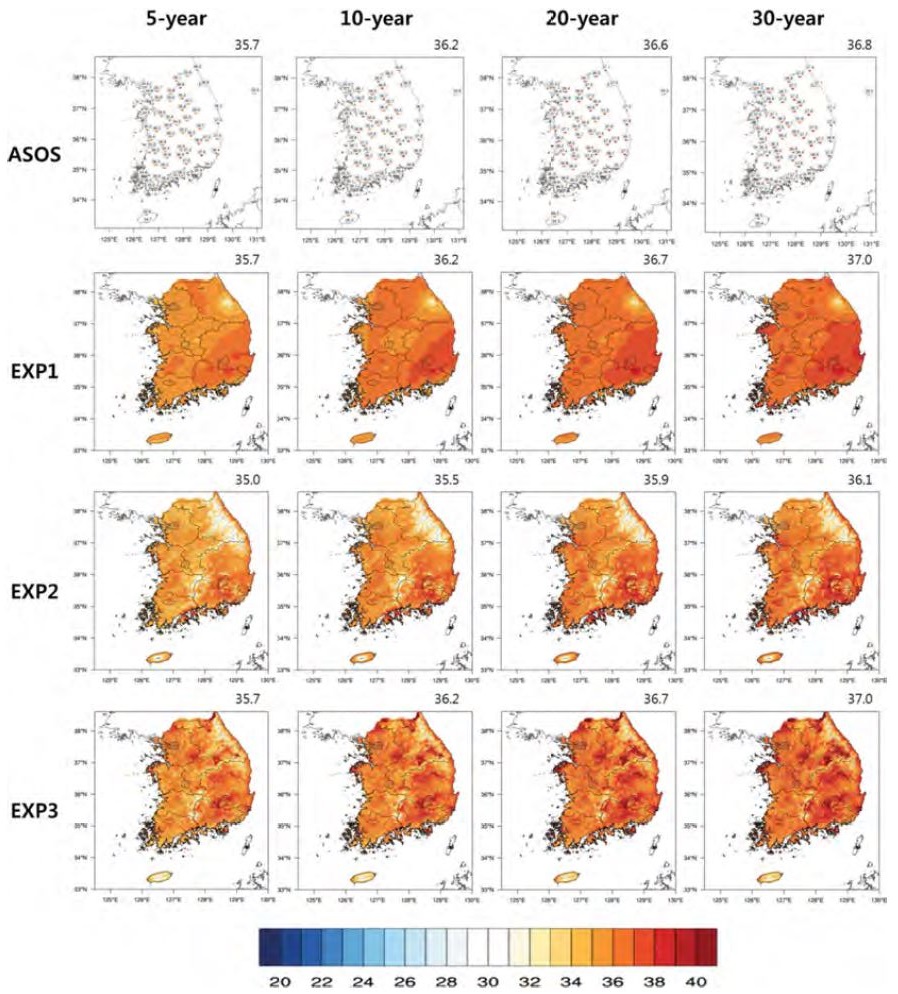
Extreme value of daily maximum temperature over South Korea that can happens once in 5, 10, 20 and 30 years (Unit: oC).

Fig. 4.

Same as in Fig. 3, but for daily minimum temperature (Unit: oC).

Fig. 5.

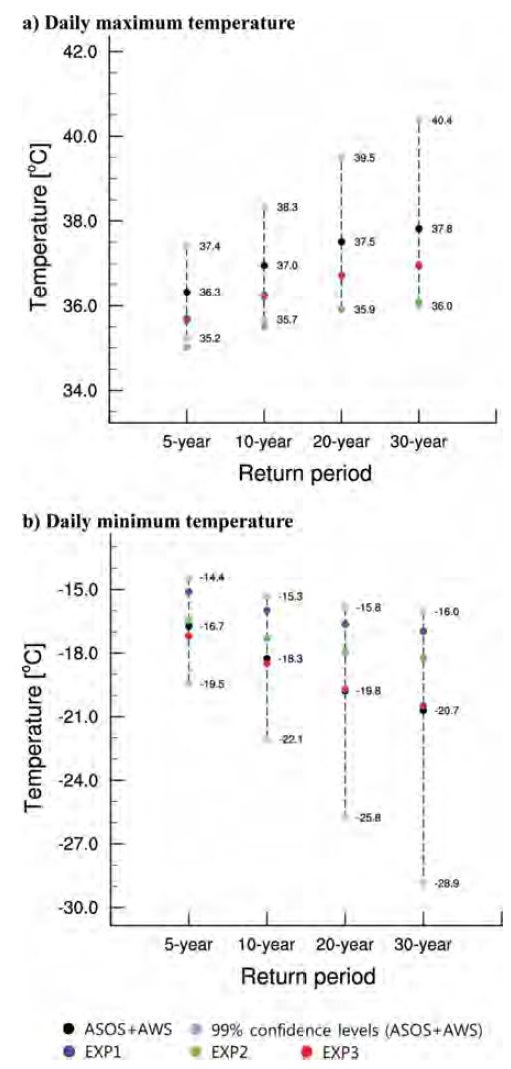
Extreme value of daily maximum/minimum temperature from ASOS + AWS. Black dot means return value and grey dots represent the 99% confidence interval of the extreme value. Blue, green, and red dots indicate EXP1, EXP2, and EXP3, respectively (Unit: oC).

최저기온의 경우, 5년, 10년, 20년, 30년과 같이 재현주기가 길어짐에 따라 ASOS를 포함한 모든 실험들의 최저기온 극한값도 점차 감소함을 보였으며, 태백산맥과 소백산맥 등 고도가 높은 지역에서 비교적 더 낮은 일 최저기온 극한값이 나타났다(Fig. 4). 각 실험 별로 살펴보면 각 재현주기에 대해 극한값이 변하는 정도가 IDW와 PRISM의 입력자료로 사용된 ASOS와 차이가 있었다. EXP1의 경우, 남한 영역의 면적평균값이 모든 재현주기에서 ASOS보다 약 0.1~0.2^oC 낮게 나타났다. 이는 ASOS + AWS에서 추정된 최저기온 극한값과 비교하여 99% 신뢰구간에 유의한 값이지만 높게 나타났다(Fig. 5b). EXP1의 최저기온 극한값의 공간분포를 살펴보면, 최고기온에서 언급했듯이 30 m 고해상도 자료임에도 불구하고 상세한 지형이 나타나지 않았다. EXP2의 경우, 상세한 일 최저기온의 극한값 분포가 나타났으며 남한 영역의 면적 평균값은 ASOS와 EXP1보다 낮게 나타났다(Fig. 4). ASOS + AWS에서 추정된 최저기온 극한값과 비교해 보면, EXP1에서 추정된 극한값이 ASOS + AWS에서 추정된 극한값보다 높게 나타났지만, 99% 신뢰구간에 유의했다(Fig. 5b). 최고기온에서 가장 좋은 결과를 보였던 EXP3의 경우, 남한 영역의 면적평균값이 다른 실험들(EXP1, EXP2)에 비해 가장 낮게 나타났으며, 이 극한값들은 ASOS + AWS에서 추정된 극한값과 가장 유사했다(Fig. 5b). 종합해보면, EXP1과 EXP2는 입력자료로 사용된 ASOS보다는 일 최저기온의 극한값을 낮게 추정했지만, AWS가 포함된 ASOS + AWS 에서 추정된 극한값 보다는 높게 추정했다. 이는 검증자료로 사용되는 320개의 AWS 지점의 극한값을 EXP1과 EXP2에서는 잘 모의하지 못한 것을 의미한다. 반면 EXP3는 60개 지점의 ASOS만 사용했음에도 불구하고 ASOS + AWS에서 추정된 극한값과 가장 유사함과 동시에 상세한 극한값 공간분포도 나타내었다. 이러한 결과는 EXP3 실험 방법이 상세한 극한값 공간분포 추정에 있어서 가장 효과적임을 의미한다.

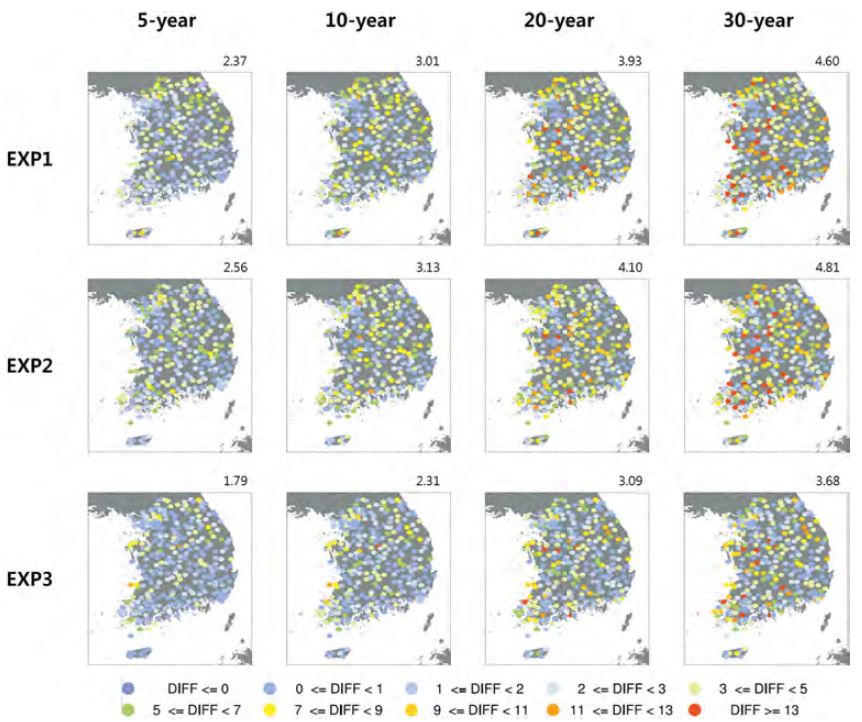
관측과 각 실험에 의해 추정된 극한값 간의 차이를 정량적으로 살펴보기 위해, 본 연구에서는 최고 · 최저 온도에 대한 AWS와 각 실험의 극한값 차이의 절대값(이하 DIFF)을 구하여 분석하였다. 각 실험에서 추정된 고해상도 자료는 AWS와 비교하기 위해 320개의 AWS 지점과 같은 위치의 값을 뽑아서 사용하였다. Figures 6과 7에는 최고 · 최저 온도에 대한 DIFF의 공간분포가 나타나있으며, Fig. 8에는 320개의 AWS 지점에 대한 DIFF의 평균값을 나타내었다. 먼저 최고기온을 살펴보면, 모든 실험들에서 해발고도가 낮은 해안가 부근에 상대적으로 낮은 DIFF를 보이는 반면, 해발고도가 높은 산맥지역에서는 비교적 큰 DIFF가 나타났다(Fig. 6). 그리고 재현주기가 길어짐에 따라 각 실험과 AWS에서 추정된 극한값과의 DIFF가 크게 나타났다. 각 실험별로 비교해보면, 재현주기에 상관없이 EXP3가 가장 낮은 DIFF를 보이며, 그 다음으로 EXP1, EXP2 순서였다(Fig. 8a). 최저기온의 경우에도 최고기온과 유사한 결과가 나타났다. 모든 실험들에서 재현주기가 길어짐에 따라 DIFF가 커졌으며, 실험들 중에서는 최고기온과 동일하게 극한값 공간분포에서 관측과 가장 유사했던 EXP3가 가장 낮은 DIFF를 보였다. 그 다음으로 최저기온의 극한값이 관측과 유사했던 실험은 EXP1, EXP2 순서였다(Fig. 8b). 그러나 최저기온의 극한값 DIFF는 최고기온의 극한값 DIFF에 비해 대략 2~3배 정도의 매우 큰 값을 보였다(Fig. 8). 그리고 앞서 분석했던, 극한값 공간분포의 면적평균 차이 또한 최저기온이 최고기온보다 높았다(Figs. 3과 4). 이렇게 실험간 최저기온의 극한값 차이가 최고기온보다 높은 이유는 Fig. 9와 같이 기온의 시간 변동성과 연관이 있다. Figure 9a는 ASOS와 AWS의 연 최고 · 최저 기온 표준편차(standard deviation)의 남한 영역 평균값이며, Fig. 9b는 일 최고 · 최저 기온을 상자그림(Box plot)으로 나타낸 것이다. 일 최고기온의 최고값과 최저값의 차이가 18.1^oC 임에 반해, 일 최저기온의 최고값과 최저값의 차이는 46.4^oC로 두 관측자료 모두 최저기온의 시간 변동성이 최고기온의 시간 변동성 보다 2.5배 이상 크게 나타났다(Fig. 9). 이처럼 최저기온의 시간 변동성이 최고기온에 비해 크기 때문에, GEV 함수에서 추정된 최저기온의 극한값 분포가 최고기온의 극한값 분포보다 넓은 범위로 추정된다. 따라서 입력자료의 기간(15년) 내에 넓은 극한값 분포를 보인 최저기온이 최고기온보다 넓은 신뢰구간 및 오차 범위를 나타냈다(극한값 오차 범위: 최고기온 0.7~1.7^oC, 최저기온1.8~4.8^oC). 특히, 최저기온의 경우 가장 성능이 좋은 EXP3의 DIFF값도 20년 이상의 재현주기에서는 3^oC 이상의 큰 편차를 보였다. 추정된 오차범위가 3^oC 이상 크게 나타날 경우 응용분야에서의 활용성이 낮아질 수 밖에 없기 때문에 재현주기를 길게 살펴보기 위해서는 최저기온과 같이 일 변동성이 큰 변수는 극한값 추정에 있어서 입력자료의 기간을 더 확장하여 분석할 필요성이 있다.

Fig. 6.

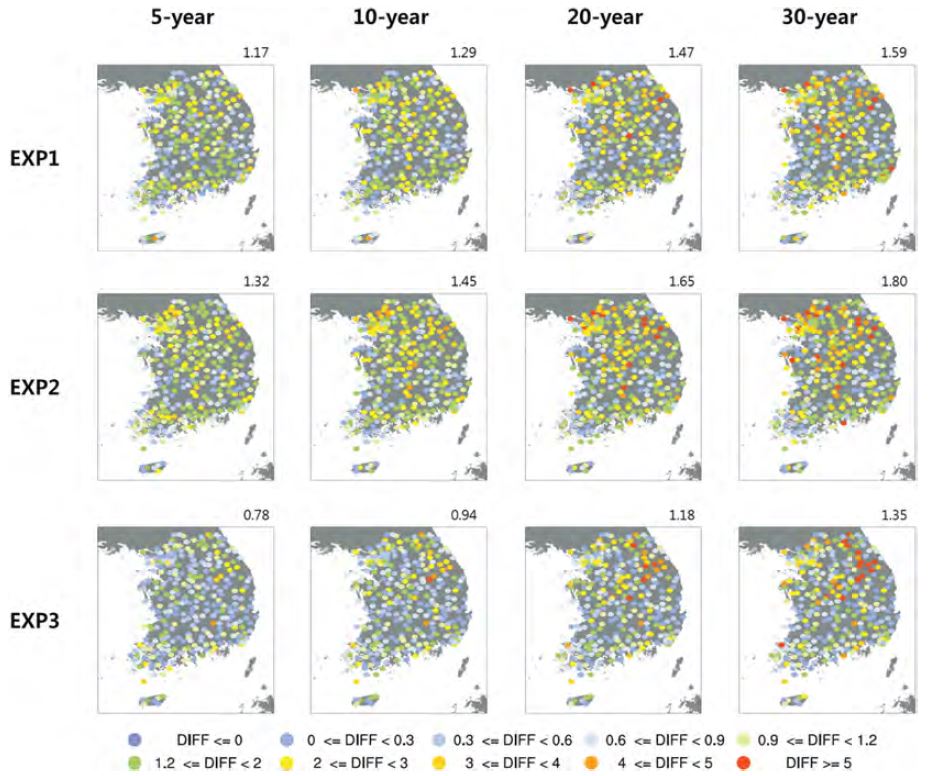
Spatial distributions of difference between estimated extreme values from AWS and each experiment for daily maximum temperature (Unit: oC).

Fig. 7.

Same as in Fig. 6, but for minimum temperature (Unit: oC).

Fig. 8.

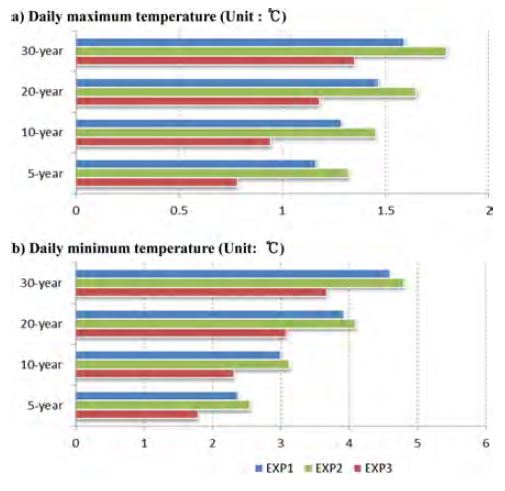
Averaged value of difference between estimated extreme values from AWS and each experiment for daily maximum (a) and minimum (b) temperature (Unit: oC).

Fig. 9.

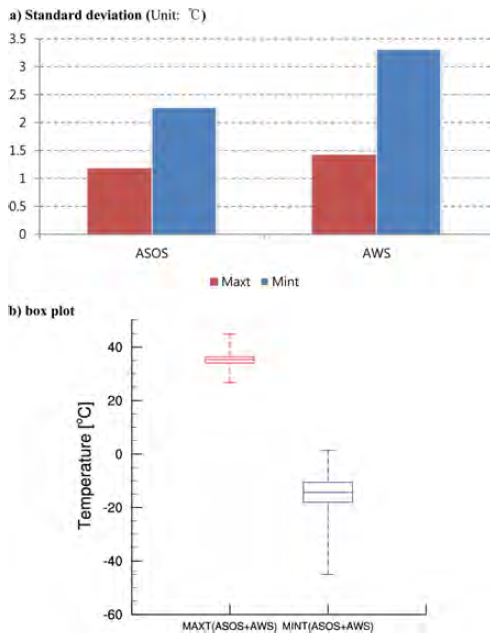
Standard deviations (a) and Box plot (b) of daily maximum (red) and minimum (blue) temperature for ASOS and AWS.

각 실험 별 DIFF에서 특이한 점은 최고기온 및 최저기온 모두 EXP1이 EXP2보다 DIFF가 낮다는 것이다. 이는 60개의 ASOS에서 극한값을 추정한 후, IDW와 PRISM을 이용하여 상세한 극한값 분포를 추정하면 IDW가 PRISM보다 관측과 유사하게 추정됨을 의미한다. 앞서 Ahn et al. (2014)에서는 30 m 고해상도 기온 자료를 추정함에 있어서 IDW보다 PRSIM이 좋은 성능을 보인다고 소개 하였으나 이러한 결과가 나타난 이유는 기온에 대한 거리, 고도, 지향면, 해양도 등의 지형학적 특성의 영향이 극한값에 미치는 영향과 다르기 때문이다. 즉, 기온의 상세화에 최적화된 PRISM을 극한값의 상세화에 적용하였기 때문에 이 같은 문제점이 발생하였다. 이를 더 자세히 설명하기 위해 최고온도(Figs. 10a-e)와 최저온도(Figs. 10f-j)의 ASOS + AWS 기후값과 5년, 10년, 20년, 30년 재현주기 극한값을 고도에 따른 분포로 나타내었다(Fig. 10).

Fig. 10.

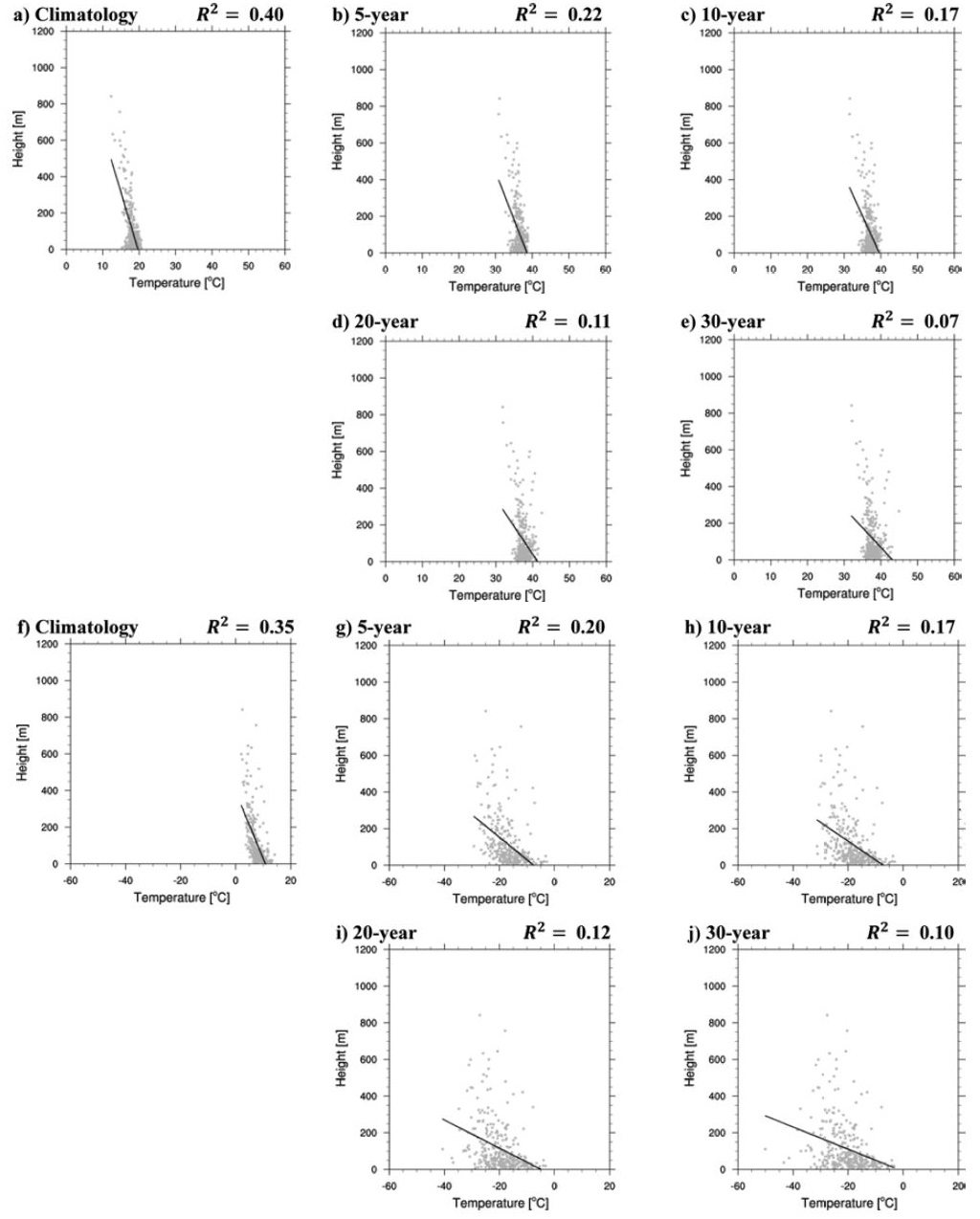
Scatter plots of altitudes against daily maximum (a-e) and minimum (f-g) temperature for ASOS + AWS. (a) and (f) indicate climatology over 15 years (1999~2013). The others represent extreme values of ASOS + AWS for each return period. Here, all panels include its regression line.

각 그림의 오른쪽 상단에 위치한 값은 결정계수(R²)를 나타낸다. 결정계수가 1에 가까울수록 고도에 따른 기온의 선형회귀모형의 결과가 ASOS + AWS와 유사함을 의미하며 고도와 온도 사이의 선형적 관계가 뚜렷함을 나타낸다. 먼저 최고기온을 먼저 살펴보면, 기후값의 결정계수는 0.40 인해 반면, 5년, 10년, 20년, 30년 재현주기의 극한값에서는 각각 0.22, 0.17, 0.11, 0.07로 재현주기가 길어질수록 낮은 결정계수를 보였다. 최저기온도 최고기온과 유사하게 나타났다. 즉, 최저기온의 기후값은 결정계수가 0.35이고, 5년, 10년, 20년, 30년 재현주기의 극한값에서는 각각 0.20, 0.17, 0.12, 0.10으로 재현주기가 길수록 점차 감소하고 있었다. 이러한 결과는 기온의 극한값의 경우 최저/최고 기온에 비하여 고도에 따른 기온의 선형회귀 모형의 적합성이 낮음을 의미한다. 따라서 극한값의 경우 일반적인 기온에 비하여 고도와의 선형적 관계가 뚜렷하지 않기 때문에, 고도와 온도와의 관계를 가중치로 사용하는 PRISM을 이용한 EXP2 방법이 EXP1보다 성능이 낮게 나타난 것으로 해석된다. 반면 PRISM을 기온에 적용한 후, 각각의 격자점에서 극한값을 구한 EXP3는 재현주기에 상관없이 다른 실험들에 비해 가장 관측과 유사한 극한값을 추정하였다. 이는 극한값이 아니라 기온에 최적화 되어 있는 PRISM으로 상세한 기온 분포를 구한 후, 각 격자점마다 극한값을 추정하는 방법이 다른 실험 방법들에 비하여 더 정확함을 의미한다.

5. 요약 및 결론

본 연구에서는 IDW, PRISM, GEV 등과 같은 통계적 기법들을 활용하여 30 m 해상도의 격자형 기온 극한값을 추정해 보고자 하였다. 실험은 최적의 극한값 추정 방법을 찾기 위해 3가지 방안으로 구성하여 수행되었다. 첫 번째 실험인 EXP1은 ASOS에서 극한값을 추정한 후, IDW로 고해상도 극한값 분포를 생산한 방법이며, 두 번째 실험인 EXP2는 EXP1과 동일하지만 IDW 대신 PRISM을 사용한 방법이다. 마지막 실험인 EXP3는 ASOS에서 PRISM을 통해 상세한 격자형 기온 자료를 만들고, 각 격자점마다 극한값을 추정한 방법이다.

최고(최저)기온의 경우, 5년, 10년, 20년, 30년과 같이 재현주기가 증가함에 따라 관측을 포함한 모든 실험들의 최고(최저)기온의 극한값도 점차 증가(감소)함을 보였다. 하지만 각 실험 방법에 따라 각 재현주기에 대한 극한값이 변하는 정도가 ASOS + AWS 에서 추정된 극한값과 차이가 있었는데, EXP1에서 추정된 최고 및 최저 기온 극한값들은 모든 재현주기에서 99% 신뢰구간에 유의했지만 공간적 분포를 살펴보면, 30 m 고해상도 자료임에도 불구하고 해발고도가 높은 지역에 동그라미 형태의 분포가 나타날 뿐 상세한 극한값 분포가 나타나지 않았다. EXP2는 최고 및 최저기온의 극한값 공간적 분포가 지형을 따라 상세하게 나타났지만, 극한값의 면적평균값의 경우 5년, 10년 재현주기에서는 최고기온의 극한값이 관측에 비해 낮게 추정되어 99% 신뢰구간에 유의하지 못했다. ASOS에서 PRISM을 통해 고해상도 격자형 자료로 생산한 후, 극한값을 추정한 EXP3는 최고 및 최저기온 극한값뿐만 아니라 공간적 분포도 다른 실험에 비해 관측과 가장 유사하게 나타났다. 추정된 상세한 극한값을 비교해 보면, 최고기온보다는 최저기온에서 관측과의 극한값 차이가 크게 나타났는데, 이는 일 최저기온의 시간 변동성이 최고기온의 시간 변동성보다 크기 때문인 것으로 나타났다.

검증자료로 사용되는 AWS와 각 실험간에 DIFF를 비교해 보면, 최고 및 최저기온 모두 재현주기가 증가함에 따라 극한값의 DIFF도 커졌다. 실험간에 DIFF를 비교해보면, 최고 및 최저기온 모두 EXP3의 DIFF가 가장 낮았으며, 그 다음으로 EXP1, EXP2였다. 여기서 PRISM을 이용한 EXP2가 IDW를 이용한 EXP1보다 극한값을 잘 모의하지 못한 이유는 최고기온과 최저기온이 아닌 기온의 극한값에 PRISM을 사용했기 때문이다. 즉, 기온의 극한값의 경우 최저/최고기온과 다르게 고도와의 관계성이 뚜렷하게 나타나지 않기 때문에(Fig. 10), 입력자료와 고도와의 관계를 이용하여 가중치를 구하는 PRISM의 결과가 IDW를 이용한 결과보다 낮게 나타난 것으로 해석된다. 그럼에도 불구하고 EXP1과 EXP2는 각 격자점마다 기온 극한값을 생산하지 않고, 60개의 극한값으로 30 m의 고해상도 격자자료로 만들었기 때문에 각 격자점의 기온 극한값을 제대로 추정하는데 한계가 있다. 반면, ASOS에서 PRISM을 통해 고해상도 격자형 기온자료를 생산한 후, 극한값을 추정한 EXP3에서는 다른 실험들에 비하여 계산을 대략 600만배 더 많이 수행하는 단점을 가지고 있지만, 최고/최저기온에 대해 모든 재현주기에서 관측과 유사한 극한값을 보였다. 이러한 결과는 통계적 기법들의 조합 및 순서를 어떻게 적용하는가에 따라 최고/최저기온의 극한값 추정 결과의 질이 달라질 수 있음을 의미한다. 이처럼 고르게 분포된 상세한 극한값 정보 생산을 통해, 우리는 폭염, 냉해 등 기온 극한값으로 발생되는 재해지역 정보를 보다 정확히 제공할 수 있을 것으로 기대한다.

Acknowledgments

이 논문은 부산대학교 기본연구지원사업(2년)에 의해서 연구되었습니다.

References

Ahn, J. B., J. L. Lee, and E. S. Im, (2012), The reproducibility of surface air temperature over South Korea using dynamical downscaling and statistical correction, J. Meteor. Soc. Japan, 90, p493-507. [https://doi.org/10.2151/jmsj.2012-404]
Ahn, J. B., J. Hur, and A. Y. Lim, (2014), Estimation of finescale daily temperature with 30 m-resolution using PRISM, Atmosphere, 24, p101-110, (in Korean with English abstract). [https://doi.org/10.14191/Atmos.2014.24.1.101]
Ahn, J. B., S. R. Jo, M. S. Suh, D. H. Cha, D. K. Lee, S. Y. Hong, S. K. Min, S. C. Park, H. S. Kang, and K. M. Shim, (2016), Changes of precipitation extremes over South Korea projected by the 5 RCMs under RCP scenarios, Asia-Pac. J. Atmos. Sci., 52, p223-236. [https://doi.org/10.1007/s13143-016-0021-0]
Barnes, S. L., (1964), A technique for maximizing details in numerical weather map analysis, J. Appl. Meteorol., 3, p396-409. [https://doi.org/10.1175/1520-0450(1964)003<0396:ATFMDI>2.0.CO;2]
Cressman, G. P., (1959), An operational objective analysis system, Mon. Wea. Rev., 87, p367-374. [https://doi.org/10.1175/1520-0493(1959)087<0367:AOOAS>2.0.CO;2]
Daly, C., R. P. Neilson, and D. L. Phillips, (1994), A statistical- topographic model for mapping climatological precipitation over mountainous terrain, J. Appl. Meteorol., 33, p140-158. [https://doi.org/10.1175/1520-0450(1994)033<0140:ASTMFM>2.0.CO;2]
Fisher, R. A., and L. H. C. Tippett, (1928), Limiting forms of the frequency distribution of the largest or smallest member of a sample, Math. Proc. Cambridge., 24, p180-290. [https://doi.org/10.1017/S0305004100015681]
Frey, H., and F. Paul, (2012), On the suitability of the SRTM DEM and ASTER GDEM for the compilation of topographic parameters in glacier inventories, Int. J. Appl. Earth Obs., 18, p480-490. [https://doi.org/10.1016/j.jag.2011.09.020]
Hong, K. O., M. S. Suh, D. K. Rha, D. H. Chang, C. Kim, and M. K. Kim, (2007), Estimation of high resolution gridded temperature using GIS and PRISM, Atmosphere, 17, p255-268, (in Korean with English abstract).
Hosking, J. R. M., (1990), L-moments: analysis and estimation of distributions using linear combinations of order statistics, J. Roy. Stat. Soc., 52, p105-124.
Im, E. S., J. B. Ahn, and S. R. Jo, (2015), Regional climate projection over South Korea simulated by the Had-GEM2-AO and WRF model chain under RCP emission scenarios, Climate. Res., 63, p249-266. [https://doi.org/10.3354/cr01292]
IPCC, (2013), Climate change 2013: The Physical Science Basis. Contribution of Working Group I to the fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, p1552.
Kim, M. K., M. S. Han, D. H. Jang, S. G. Baek, W. S. Lee, Y. H. Kim, and S. Kim, (2012), Production technique of observation grid data of 1 km resolution, Climate Res., 7, p55-68, (in Korean with English abstract).
Kim, M. K., D. H. Lee, and J. Kim, (2013), Production and validation of daily grid data with 1km resolution in South Korea, Climate Res., 8, p13-25, (in Korean with English abstract).
Park, J. S., and H. S. Jung, (2002), Modelling Korean extreme rainfall using a Kappa distribution and maximum likelihood estimate, Theor. Appl. Clim., 72, p55-64. [https://doi.org/10.1007/s007040200012]
Rider, N. E., J. R. Philip, and E. F. Bradley, (1963), The horizontal transport of heat and moisture - a micrometeorological study, Quart. J. Roy. Meteor. Soc., 89, p506-531. [https://doi.org/10.1002/qj.49708938207]
Schoof, J. T., and S. C. Pryor, (2001), Downscaling temperature and precipitation: a comparison of regression based methods and artificial neural networks, Int. J. Climatol., 21, p773-790. [https://doi.org/10.1002/joc.655]
Szolgay, J., J. Parajka, S. Kohnová, and K. Hlavčová, (2009), Comparison of mapping approaches of design annual maximum daily precipitation, Atmos. Res., 92, p289-307. [https://doi.org/10.1016/j.atmosres.2009.01.009]