모델 예측변수들을 이용한 집중호우 예측 가능성에 관한 연구
Abstract
In order to determine the prediction possibility of heavy rainfall, a variety of analyses was conducted by using three-dimensional data obtained from Korea Local Analysis and Prediction System (KLAPS) re-analysis data. Strong moisture convergence occurring around the time of the heavy rainfall is consistent with the results of previous studies on such continuous production. Heavy rainfall occurred in the cloud system with a thick convective clouds. The moisture convergence, temperature and potential temperature advection showed increase into the heavy rainfall occurrence area. The distribution of integrated liquid water content tended to decrease as rainfall increased and was characterized by accelerated convective instability along with increased buoyant energy. In addition, changes were noted in the various characteristics of instability indices such as K-index (KI), Showalter Stability Index (SSI), and lifted index (LI). The meteorological variables used in the analysis showed clear increases or decreases according to the changes in rainfall amount. These rapid changes as well as the meteorological variables changes are attributed to the surrounding and meteorological conditions. Thus, we verified that heavy rainfall can be predicted according to such increase, decrease, or changes. This study focused on quantitative values and change characteristics of diagnostic variables calculated by using numerical models rather than by focusing on synoptic analysis at the time of the heavy rainfall occurrence, thereby utilizing them as prognostic variables in the study of the predictability of heavy rainfall. These results can contribute to the identification of production and development mechanisms of heavy rainfall and can be used in applied research for prediction of such precipitation. In the analysis of various case studies of heavy rainfall in the future, our study result can be utilized to show the development of the prediction of severe weather.
Keywords:
Severe weather, heavy rainfall, KLAPS reanalysis data, convective system, diagnosis, prognostic prediction1. 서 론
우리나라의 집중호우는 발달한 저기압, 태풍, 장마전선, 고온다습한 북태평양고기압 가장자리의 수렴대 등에서 주로 나타나며, 6월에서 9월 사이에 많이 발생한다. 똑같이 150 mm의 비가 내린다고 해도 강수의 집중성, 규모, 나타나는 지역, 지속시간 등 어떠한 기상시스템과 연관되어 있느냐에 따라 큰 차이가 있으며, 이로 인한 피해 정도도 다르다. 집중호우는 주로 강한 상승기류에 의해 형성되는 적란운에서 주로 발생하며, 풍부한 수증기의 공급과 온난 다습한 공기가 상승할 수 있는 조건이 형성되면 집중호우 발생 가능성이 높다. 또한 성질이 다른 커다란 공기 덩어리가 만나는 경계인 전선이나 하층에서 공기가 모여들어 수렴하는 수렴대 등에서는 지리적 여건과 상관없이 집중호우가 발생한다.
집중호우를 유발하는 주요 요소는, 이류되는 많은 수증기량, 강한 연직 상승류, 그리고 정적 불안정도 등이다(Maddox, 1979). 강한 대류불안정과 대기 하층의 강한 연직바람시어(Vertical Wind Shear)의 존재는 스톰이 발생하기 좋은 조건이 된다. 대류불안정은 강한 스톰이 발생할 수 있는 가능성에 대한 정보를 제공하고 하층 연직 바람시어는 발생한 스톰의 형태와 지속 시간을 결정하는데 주로 이용된다(Kim and Ham, 2009). 현업이나 예보를 위한 집중호우 예측(진단)은 대류가용잠재에너지(Convective Available Potential Energy: CAPE; Doswell and Rasmussen, 1994), 불안정 파라메터(Instability parameters - Lifting Condensation Level, Lifted Index, Convective Inhibition), 바람쉬어(Wind Shear; Richardson et al., 2007), Storm-Relative Helicity (SRH) 등이 주로 활용되고 있다.
불안정지수는 두 개 이상의 기압면의 온도, 이슬점 온도 등을 이용하여 대기의 불안정한 정도를 나타내기 위하여 만들어진 것으로, 집중호우의 특성이나 예측을 위해서 많은 종류의 불안정지수가 개발되어 사용되고 있다. K-index (KI: George, 1960)는 주로 여름철 해양성 열대기단의 영향을 받을 때 나타나는 호우와 뇌우를 진단하기 위해 개발되었다. 이 지수는 중층이하 대기층의 불안정 요소를 진단하기 위해 3개 층의 기온과 2개 층의 노점온도를 사용한다. 해양성 열대기단인 북태평양 고기압의 영향을 받는 여름철 호우 및 뇌우 진단을 위해 KI를 활용할 수 있다. Showalter Stability Index (SSI: Showalter, 1953)는 계산식이 간단하고 편리하여 일반적으로 대기불안정 상태를 진단하고 예측하는데 많이 활용되고 있다. 하지만, 역전층이 존재하거나 수증기가 급격히 감소하는 경우에는 오차가 발생하는 경우가 많다. Lifted index (LI)는 850 hPa 등압면을 지나는 역전층 또는 수증기가 급격하게 감소하는 층이 있는 경우에 SSI를 수정 적용하기 위하여 개발되었다. 일반적으로 LI는 SSI 값보다 약간 작은 경향이 있다.
Djuric (1994)은 위험기상에서 CAPE의 값은 넓은 범위에서 분포하여 나타나고, 대략 1,000 m2 s−2 이하에서는 강한 대류 발생 가능성이 적고, 강한 스톰이 발달할 때는 2,000 m2 s−2 이상일 때도 있다고 하였다. Kim et al. (2012)은 북태평양 고기압이 확장하여 한반도에 영향을 미칠 때 CAPE가 420~1,700 J kg−1 정도로 높은 값이 나타남을 보였으며, 정체전선 상에서는 대체로 CAPE가 발생하지 않았고, 태풍의 간접적인 영향을 받을 때는 CAPE가 50~1,000 J kg−1의 범위에서 분포한다고 하였다. Kim et al. (2009)은 장마기간의 집중호우가 대류가용잠재에너지의 증가보다 SRH와 더 밀접한 관계가 있다고 하였으며, 특히 SRH가 150 m2 s−2 이상일 때 강수가 발생하였고, 값이 클수록 강수량이 증가한다고 하였다. 또한 Kwon et al. (2013)은 영서와 영동의 10년간(2001년~2010년)의 집중호우현상을 분석하여 영동 호우에서는 CAPE가 발생하지 않는 반면, 영서에서는 1,000 J kg−1 이상의 CAPE와 100~450m2 s−2의 SRH가 나타난다고 하였다. Kim and Ham (2009)은 집중호우 사례 모의를 통하여 CAPE가 낮더라도 강한 상승류가 유지될 수 있음을 보였고, 집중호우 예측에 불안정지수보다 CAPE, SRH, 그리고 벌크-리처든 수(bulk-Richardson number, BRN)가 한반도에서 발생하는 집중호우를 예측하는데 더 적합한 지수라고 하였다. Park and Lee (2008)는 장마전선 상에서 발생한 집중호우사례를 분석하여 열 · 역학적 불안정에 기인하여 대류운이 발달하고 특히, 높은 CAPE와 대류억제(Convective Inhibition, CIN)에 의해 부력 에너지가 집중되어 강한 대류운으로 성장할 수 있다고 하였다.
이들 대부분의 연구는 특정지역이나 집중관측 등을 통한 제한된 영역(시간적, 공간적)에 대한 분석이거나, 집중호우 유형에 따라서 이를 유발한 요인들(ingredients)이 다르게 나타남으로 인해 어떠한 요인이 집중호우 발생에 주요하게 작용했는지 파악할 필요가 있다(Jung et al., 2015). 또한 예측변수들은 대기의 상태를 평가하는데 유용할 수 있으나, 일괄적으로 적용하는 데는 아직 한계가 있다. 예를 들면, 불안정 지수의 일종인 SSI, KI 등은 850 hPa 이하 층의 습기 및 역전층 등을 나타낼 수 없는 등 변화된 대기의 불안정을 잘 반영하지 못하는 한계가 있다. CAPE와 SRH 등도 집중호우 유형이나 기상 조건에 따라 변화가 다양하게 나타난다. 이렇듯 기존의 집중호우 예측변수만을 이용한 예측보다는 추가적으로 집중호우 예측에 도움을 줄 수 있는 예측변수를 추가함으로서 집중호우의 예측성을 향상시킬 수 있는 방법의 모색이 필요하다. 또한 집중호우 유형에 따른 집중호우 예측변수의 변동특성에 대한 고찰도 필요하다.
따라서 본 연구에서는 고해상도 수치모델에서 산출되는 다양한 변수들(역학변수, 열역학변수)의 정량적 값들을 추출하여 시간에 따른 변동 특성이나 경향 등에 대해 분석하였다. 이를 통하여 집중호우 발생과 연관성이 있는 변수들을 살펴보고, 이러한 변수들의 변동 특성 등을 이용하여 집중호우의 예측이나 진단 등에 활용할 수 있을지에 대해서 분석하였다.
2. 자료 및 방법
본 연구에서 사용된 자료는 한반도 영역을 중심으로 5 km 간격의 수평해상도와 50 hPa 간격의 연직해상도로 1시간 간격으로 생산되는 KLAPS 재분석 자료(NIMS, 2009; NIMS, 2012; Jang et al., 2016)를 사용하였다. KLAPS 재분석 자료는 하나의 층이 235 × 283의 수평 격자로 구성되어 있으며, 변수에 따라 1~23개의 연직 층으로 각각 구성되어 있다. 산출되는 변수는 기온, 습도, 바람, 기압, 강수량, 비습, 구름에 관한 정보(운저, 운고, 수액함량 등) 등 총 46 종류의 자료를 생산한다. 그 중에서 집중호우 발생과 연관성이 있다고 판단되는 변수를 선별하였다.
KLAPS 재분석 자료는 3차원 격자 자료로서 집중호우 발생지점에서의 각종 변수의 정량적 값과 연직값들을 추출할 수 있다. KLAPS 재분석 자료에서 생산되는 46종류의 변수를 대상으로 집중호우 발생지점에서의 연직 값을 추출하였다. Figure 1은 KLAPS 재분석 자료의 전체 영역 및 집중호우 발생지점에서의 변수 추출 방법을 나타낸 것이다. 집중호우 발생지점 격자에서 추출한 변수는 기온, 습도, 비습, 온위, 상당 온위, 풍향, 풍속, 운저, 운고, 온도 및 온위이류, 누적 수함량분포, Storm-Relative Helicity, 불안정지수, 부력에너지 등이다. 이 중에서 온위, 상당온위, 수분 수렴, SRH, 온도 및 온위 이류 등은 지상 1개 층 자료만 산출된다. Table 1은 집중호우 예측변수(Prognostic variable)로의 활용과 예측 가능성 파악을 위하여 산출된 변수의 간단한 설명을 나타낸 것으로, 각각의 변수명, 수평 및 연직 해상도 등을 명시하였다. 집중호우 영역의 연직 변수의 분석은 집중호우 예측에 기여할 수 있는 예측변수를 선별하고 변화 특성을 파악하는데 사용된다. 또한, 한 지점에서 추출된 변수의 분석에서 변동성이 상대적으로 큰 값들이 나타난 지점은 집중호우 발생지점 중심으로 9개 격자에 대한 값도 평균하여 추출하였으며, 한 지점에서의 변수 값과 서로 비교하였다.
분석에 사용된 사례는 수도권을 중심으로 발생한 집중호우 사례에서 선정하였으며, 지상강수량은 집중호우 발생지점의 AWS 자료를 활용하였다. 분석에 사용된 AWS 지점은 남현 AWS (37o 27' N, 126o 59' E), 이천 AWS (37o 15' N, 127o 29' E), 고잔 AWS (37o 19' N, 126o 49' E)이다.
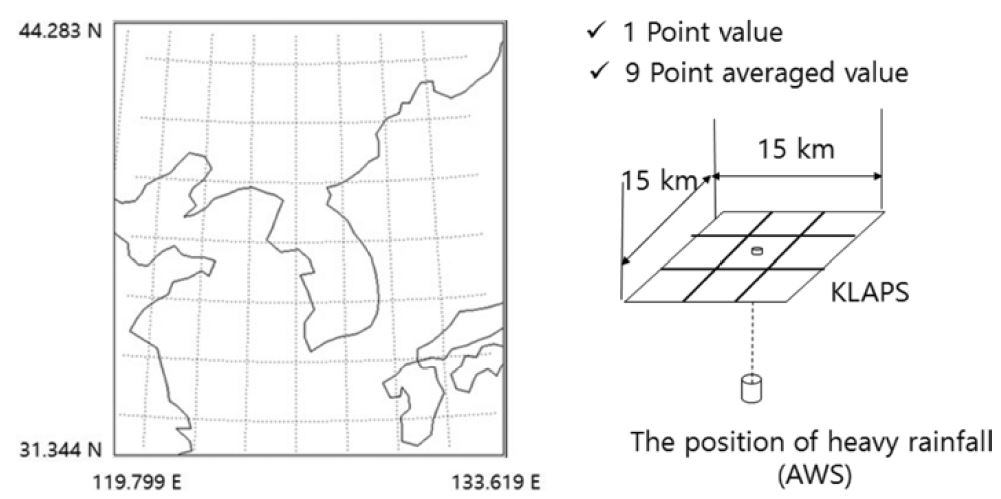
Schematic diagram of the domain region and grid structure used for the extraction of variables in the Korea Local Analysis and Prediction System (KLAPS) re-analysis data.
3. 집중호우 유형
2010년부터 2013년까지 수도권을 중심으로 발생한 집중호우 사례 중 시간당 강수량이 50 mm 이상인 집중호우 사례 중 유형의 차이가 확연하게 보이는 서로 다른 세 개의 사례를 선별하여 분석을 수행하였다. 선별된 사례는 2011년 7월 27일 0100 LST~0900 LST(case 1), 2010년 9월 21일 1400 LST~2400 LST (case 2), 2013년 9월 13일 0100 LST~1400 LST (case 3) 이다. Figure 2는 선별된 세 사례 지점에서의 시간 강수량 변화와 일누적 강수량 변화를 나타낸 것이다. Case 1은 시간당 15 mm 이상의 강한 강수가 0100 LST부터 지속적으로 내리다가 0800 LST와 0900 LST에 시간당 80 mm 이상의 강수가 급격하게 내린 사례이다. Case 2는 1400 LST에서 시작된 약한 강수가 2000 LST에 급격하게 강해지면서 시간당 거의 100 mm 가까이 집중호우가 내린 사례이다. Case 3은 국지적으로 발달하는 대류셀에 의해 0400 LST (약 38 mm hr−1)와 1200 LST (약 58 mm hr−1)에 강한 강수가 내린 사례이다. 선별된 세 사례는 라인형 대류 시스템, shallow convective 형태의 대류시스템, 그리고 국지성 대류셀에 의한 집중호우로서 각각 유형이 서로 다른 사례이다.
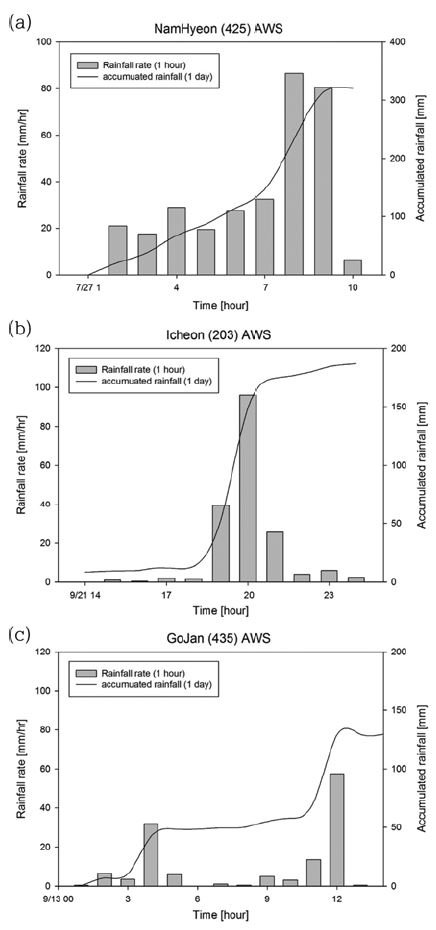
The distribution of hourly precipitation (bar charts) and cumulative daily precipitation (solid line) measured by automatic weather systems (AWS). (a) NamHyeon (37o 27' N, 126o 59' E) in Seoul (27 July 2011, 0100 LST~0900 LST), (b) Icheon (37o 15' N, 127o 29' E) in Gyeonggi-do (21 September 2010, 1400 LST~2400 LST), (c) GoJan (37o 19' N, 126o 49' E) in Gyeonggi-do (13 September 2013, 0100 LST~1400 LST).
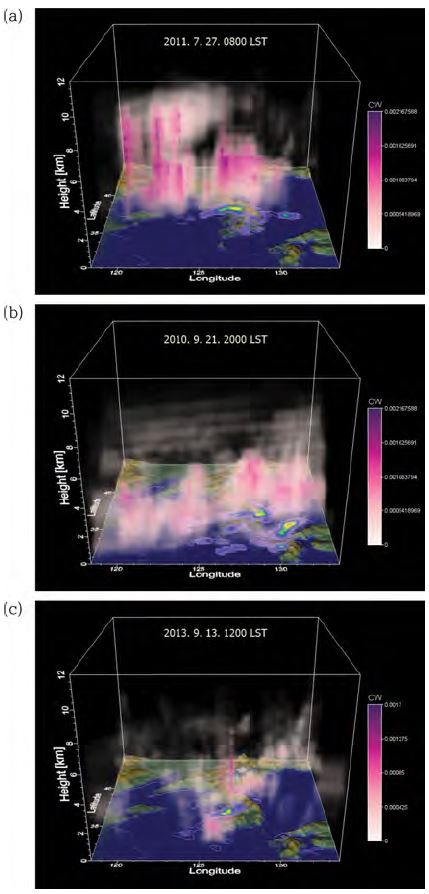
세 사례의 유형을 파악하기 위하여 선별된 세 사례 중 강수량이 가장 높게 나타났던 시점에서의 구름 수액함량(Cloud liquid water)과 지상강수량 분포를 3차원 영상으로 Fig. 3에 나타내었다. 구름 수액함량은 구름 속에 존재하는 수액의 양을 나타내는 것으로, 구름의 형태로 표현하였다. Figure 3a는 2011년 7월 27일 0800 LST에서의 구름 분포와 지상강수량 분포를 나타낸 것으로 집중호우 발생지점인 수도권을 중심으로 라인 형태[Line-shaped convective system, Kato(1998)]의 강한 구름 수액함량을 가지는 구름에 의해 집중호우가 발생하였으며, 서해상에서 지속적으로 발생하는 라인 형태의 구름들이 계속적으로 유입되었던 사례이다. Figure 3b는 2010년 9월 21일 2000 LST의 3차원 영상으로서 구름 두께가 상대적으로 얇은 전선형 구름들이 서에서 동으로 길게 분포하고 있으며, shallow convection 형태의 구름에 의해 지역적으로 강한 강수가 내렸다. Figure 3c는 2013년 9월 13일 1300 LST에서의 영상으로서 집중호우가 발생한 지점 상공에 강한 수액함량을 가지는 국지적으로 발달한 대류성 구름이 존재하고 있으며, 이로 인해 국지적으로 집중호우가 내린 사례이다. 이렇듯 집중호우 유형이 서로 다른 세 사례에 대해 집중호우 발생지점에서의 변수를 추출하고 분석을 수행하였다.
4. 결 과
수치모델 결과물에서 산출되는 다양한 변수를 집중호우 예측변수로 활용 가능한지에 대해 알아보기 위하여 집중호우 발생지점에 대한 KLAPS 재분석 자료에서 생산되는 각종 변수를 정량적으로 추출하여 분석하였다. 선별된 세 사례에서의 운저(Cloud base), 운고(Cloud top), 누적수함량(Integrated liquid water), 온도 및 온위 이류(Temperature and Potential temperature advection), 부력에너지(Buoyant energy), 불안정 지수(Instability index), Storm-Relative Helicity 등의 변화특성을 분석하였다.
4.1 구름 두께(Cloud thickness)
구름 두께(cloud height or thickness)는 운저(cloud base)에서부터 운고(cloud top)까지의 거리(Huschke, 1970)를 의미하며, 구름으로부터 생성되는 강수의 세기와 관련이 있으며, 적란운과 같은 두께가 10 km에 달하는 deep clouds는 좀 더 강한 강수를 내리게 하는 경향이 있다(Spellman, 2013). 강수의 세기와 구름두께와의 연관성을 파악하기 위하여 세 사례에 대한 집중호우 발생지점에서의 1시간 강수량, 운저, 운고의 분포(Fig. 4)를 비교하였다.
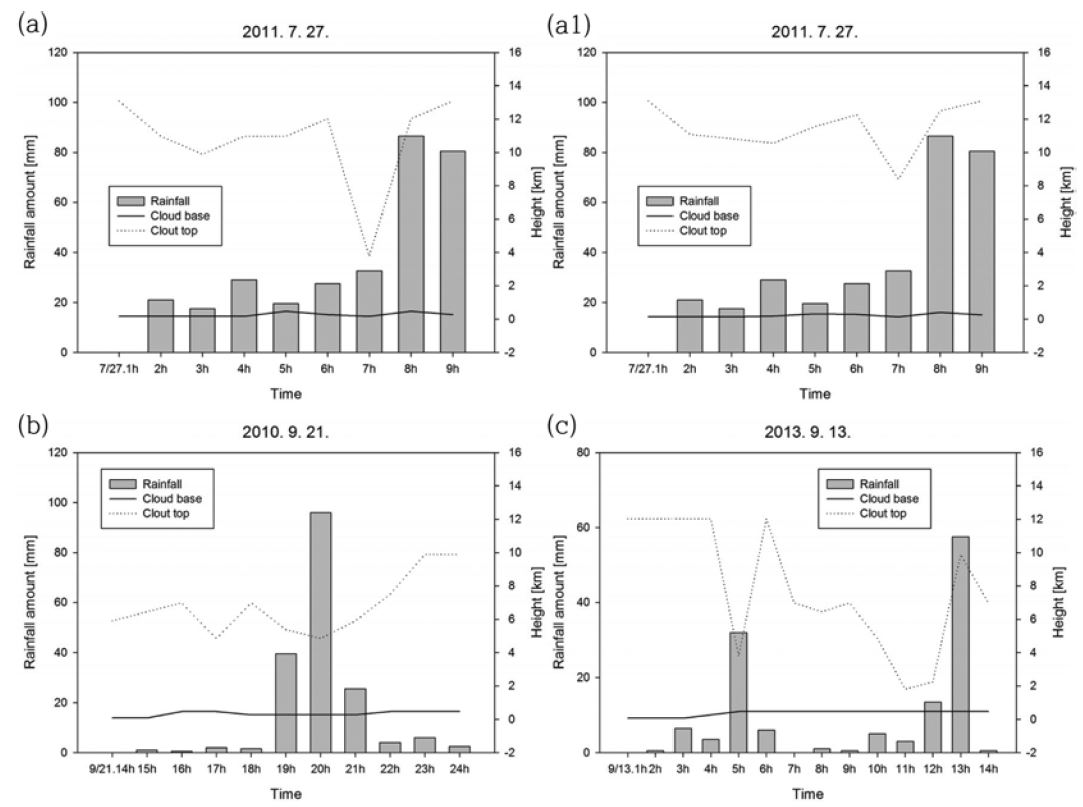
The distribution of hourly precipitation by AWS (bar charts), cloud base (solid line), and cloud top (dot line) at the heavy rainfall region (a) from 0100 LST to 0900 LST on 27 July 2011, (b) from 1400 LST to 2400 LST on 21 September 2010, (c) from 0100 LST to 1400 LST on 13 September 2013. (a1) The distribution of mean value at the nine grids near the heavy rainfall region from 0100 LST to 0900 LST on 27 July 2011.
Figure 4a는 case 1의 1시간 강수량, 운고, 운저 분포로서, 7월 27일 0700 LST를 제외하고는 거의 모든 시간대에서 10 km 이상의 구름 두께를 가지는 구름에서 강수가 내린 사례이다. 서해상에서 발달한 라인형태의 대류성 구름이 집중호우 발생지점으로 유입되면서 강수가 지속되었고, 시간당 80 mm 이상의 강수가 내린 0800 LST와 0900 LST에서는 거의 구름 두께가 12 km 정도까지 나타났다. 0700 LST에서의 급격하게 cloud top의 값이 낮아진 원인을 살펴보기 위하여 집중호우 발생지점을 중심으로 9개 지점의 평균값을 Fig. 4a1에 나타내었다. 0700 LST에서 9개 지점의 평균 cloud top의 고도가 8.38 km로 나타났으며, 이는 0700 LST에서 산출된 집중호우 발생지점에서의 cloud top 값이 너무 작게 나타났음을 확인하였다. 다른 변수들에 대해서도 변동성이 크게 나타나는 지점의 값은 9개 격자의 평균값과 비교하여 분석하였다. 다른 변수들의 비교 결과, 9개 지점의 평균으로 인해 값의 차이는 있지만, 변화 경향이나 전체적인 패턴은 집중호우 발생지점의 값과 유사하게 나타남을 확인하였다. Figure 4b는 case 2의 시간당 강수량, 운저, 운고의 분포를 나타낸 것으로, 집중호우가 내린 9월 20일 2000 LST에서의 구름 두께는 약 5 km 정도로 상대적으로 두께가 얇은 구름에 의한 shallow convective system에 의한 강수임을 알 수 있다. Figure 4c는 case 3의 시간당 강수량, 운저, 운고의 분포를 나타낸 것으로, 구름 두께의 변동이 다양하게 나타났으며, 1200 LST에서는 거의 10 km 정도의 구름 두께에서 강한 강수가 내렸으며, 3차원 분석의 결과처럼 국지적으로 발달한 대류셀이 집중호우 발생지점을 통과하면서 구름의 두께가 다양하게 변화하였다.
세 사례의 분석 결과, 약 5 km~10 km 이상의 구름두께를 가지는 대류성 구름에서 강한 강수가 내렸으며, 최소 5 km 이상의 두께를 가지는 대류형 구름에서 좀 더 강한 강수가 내림을 알 수 있다. 향후 집중호우 사례들의 추가 비교를 통하여 구름 두께와 집중호우와의 연관성에 대해 세밀히 파악해 볼 필요가 있다.
4.2 누적 수함량(Integrated liquid water)
누적수함량(Integrated liquid water)은 집중호우 발생지점의 공간상에 존재하는 수액(water)의 양을 대표하는 값으로서, 누적수함량을 이용하여 우박의 크기 및 강도를 탐지하거나 악기상(스톰)의 예측 등에 활용하기도 한다(Greene and Clark, 1972; Edwards and Thompson, 1998). 누적수함량이 높다는 것은 집중호우가 발생될 가능성이 높아진다는 것을 의미한다.
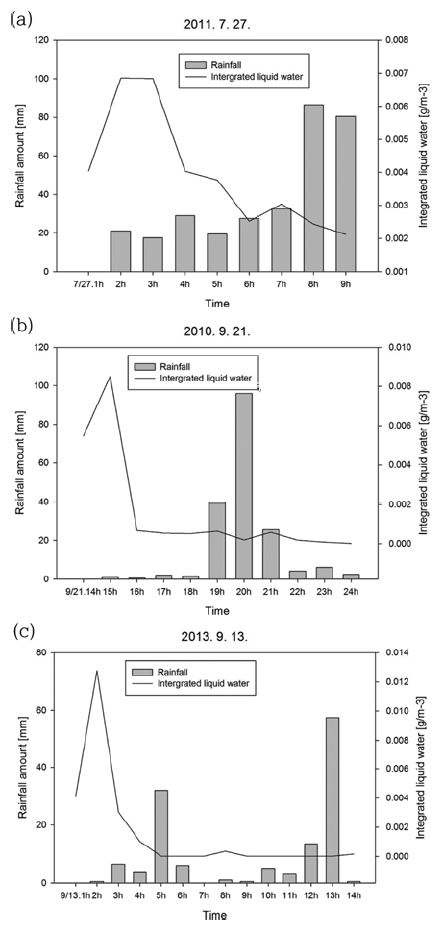
Figure 5는 세 사례에서의 시간강수량과 누적수함량 분포를 각각 나타낸 것이다. 세 사례 모두 누적수함량은 강수가 시작되기 전에 급격하게 증가하기 시작하여 집중호우 발생시점 전에 최대값(0.0069 g m−3, 0.0085 g m−3, 0.0128 g m−3)이 나타났고, 강수가 내리기 시작하면서 급격한 감소가 나타났다. 이러한 증감은 강수시스템의 유형과는 상관없이 모든 사례의 집중호우 발생 전에 나타났다. 이러한 누적수함량 분포의 증가와 급격한 감소가 발생한다면, 집중호우가 내릴 가능성이 높음을 짐작할 수 있다. 즉 누적수함량의 급격한 증감은 집중호우 발생의 전조 현상으로서, 이를 이용하면 집중호우의 예측이나 진단에 활용할 수 있을 것이다. 하지만, 구름의 종류에 따른 수액함량의 값을 제시했던 Tompson (2007)의 연구 결과와 비교해 보면, 수액함량의 값이 전체적으로 작게 나타났다. 전체적으로 낮은 누적수액함량의 결과가 지역적인 차이인지 유형의 차이인지에 대한 추가 분석도 필요할 것이다.
4.3 부력에너지(Buoyant energy)
재분석 자료에서 산출되는 변수는 양의 부력에너지(Positive Buoyant Energy)와 음의 부력에너지(Negative Buoyant Energy)가 있으며, 양의 부력에너지는 CAPE(Convective Available Potential Energy)를, 반대로 음의 부력에너지는 CIN (Convective Inhibition)을 의미한다.
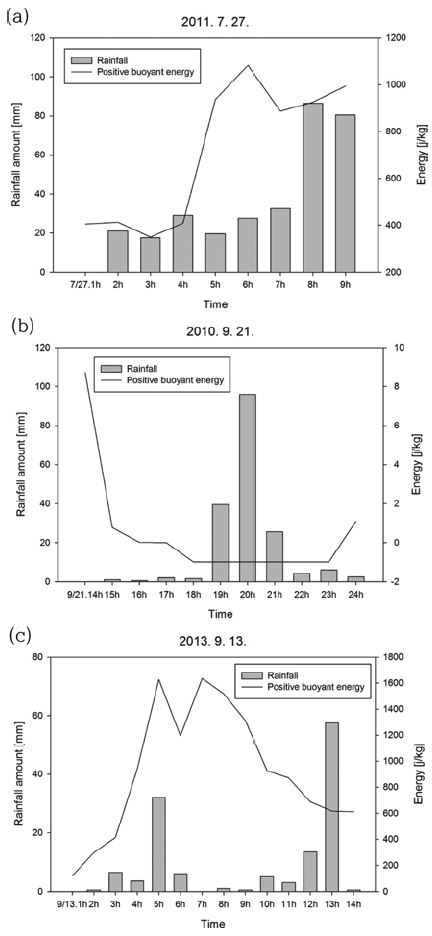
Figure 6은 세 사례의 시간강수량, 양의 부력에너지의 분포를 비교하여 나타낸 것이다. Case 1의 경우, 집중호우가 내리기 전인 0500 LST와 0600 LST에 양의 부력에너지의 급격한 증가와 최대값(1082.5 J kg−1)이 나타났다. Case 2의 경우에는 집중호우가 내린 2000 LST 전에 양의 부력에너지가 최대값(8.726 J kg−1)에 도달한 후 집중호우가 내리면서 급격하게 하락하였다. Case 3의 경우에는 집중호우가 내리기 5시간 전에 부력에너지의 최대값(1636.65 J kg−1)이 나타났으며, 시간이 지날수록 하락하였다. 양의 부력에너지는 국지성 집중호우가 내렸던 case 3에서 가장 높게 나타났고, case 2에서 가장 낮게 나타났다. 서론에서 제시했던 정체전선과 영동지역 호우에서 CAPE가 낮게 나타난 것처럼 case 2에서도 CAPE의 값이 아주 낮게 나타났다. 그림에서 보듯이, 양의 부력에너지의 급격한 증가는 대류운동의 증가로 인해 강한 구름이 급격하게 발달하게 되는 원인으로 작용했음을 짐작할 수 있다. 따라서 집중호우가 발생하기 몇 시간 전에 양의 부력에너지의 급격한 증가가 있다면, 집중호우가 발생될 가능성이 높음을 예상할 수 있다. 강수시스템의 종류에 따라 다소 차이는 있겠지만, 구름이 강수가 되어 내리기 위해서는 부력에너지의 급격한 증가로 인해 대류형 구름이 충분히 생성된 후, 어느 정도의 지연 시간(delay time)동안 발달한 후에 집중호우가 내림을 예상할 수 있다. 비록 정확하게 몇 시간 전에 얼마만큼의 부력에너지가 증가하는지는 다른 집중호우 사례에 대한 추가 분석을 통해 결정해야겠지만, 수치모델 결과물의 격자단위 실시간 모니터링을 통해 양의 부력에너지의 증가 후 급격한 감소가 발생하는 지점이 감지된다면, 집중호우 발생지점에 대한 예측에 활용할 수 있을 것이다.
4.4 온도 및 온위 이류(Temperature & potential temperature advection)
온도이류(temperature advection)는 바람의 수평 이동에 의한 온도의 변화를 야기한다. 온도이류는 크게 한랭이류(cold air advection)와 온난이류(warm air advection)로 나누어지며, 저기압의 이동방향의 전면에서 온난이류에 의해 온도이류가 상승하고 집중호우를 유발할 수 있다. 온난이류가 유입된다는 것은 유입되어 수렴하는 지점에서 대류가 활발해 진다.
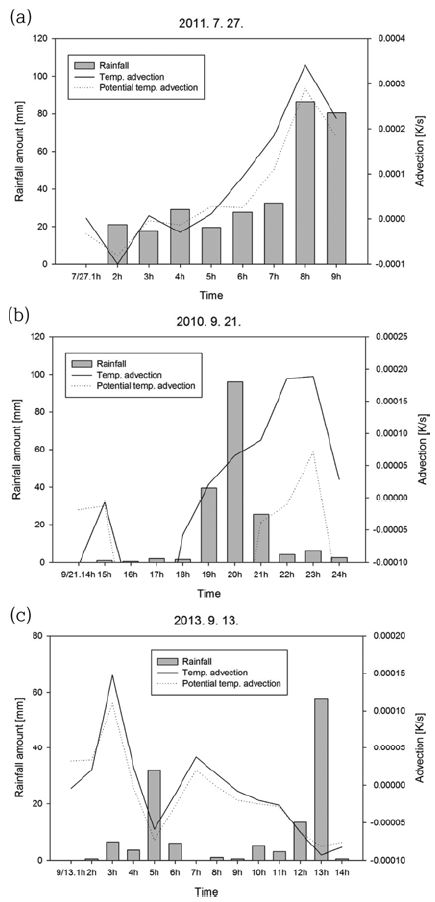
Figure 7은 세 사례에서의 시간 강수량, 온도이류, 온위이류의 분포를 나타낸 것이다. Case 1과 case 2는 강수가 시작되는 시점에 낮은 온도이류와 온위이류 값이 시간이 지남에 따라 급격하게 증가하는 것을 확인할 수 있다. Case 1은 시간강수량이 최대였던 27일 0800 LST에서 최대값(0.000342 K s−1)으로 나타났으며, 이후에 다시 감소하는 경향으로 나타났다. Case 2는 집중호우가 내리기 전에 최소였던 이류 값이 급격하게 증가하여 나타났으며, 최대 강수량이 내린 2000 LST 이후에 최대값(0.000189 K s−1)이 나타났다. 즉 집중호우가 발생되기 전에 상대적으로 낮았던 이류 값이 집중호우가 발생되기 전에 급격하게 증가하는 것을 알 수 있다. 이러한 급격한 증가 또한 집중호우의 발생과 연관이 있으며, 집중호우의 특성이라고 할 수 있다. 하지만, case 3은 case 1과 case 2와는 다르게 집중호우 발생 시점에 최소값이 나타났다. 집중호우 발생 전에 급격하게 증가한 이류 값이 집중호우 내리면서 급격하게 감소하는 것으로 나타났다. 전선 형태의 집중호우에서는 온도이류와 온위이류의 급격한 증가가 생기는 반면, case 3의 결과와 같이 국지성 집중호우에서는 이류 값이 급격하게 하락하는 특성이 있는 것으로 예상되며, 다른 국지성 집중호우 사례의 추가 분석을 통하여 확인해 볼 필요가 있다. 서로 다른 집중호우 시스템에서의 특징일수도 있지만, 온도이류와 온위이류의 증가는 집중호우와 연관이 있으며, 이를 활용하면 집중호우를 사전에 예측할 수 있을 것이다.
4.5 불안정 지수(Instability index)
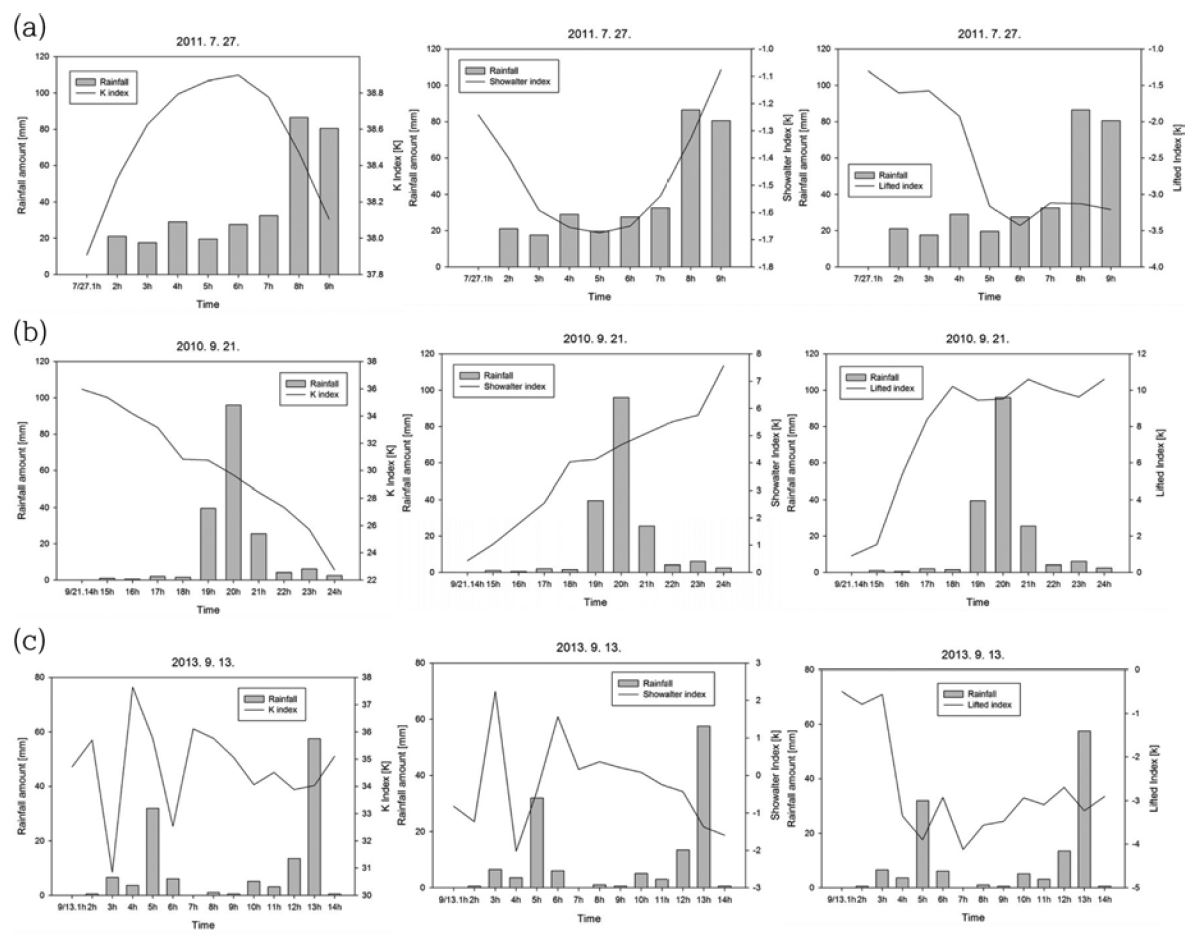
Figure 8은 세 사례에서의 각종 불안정 지수(KI, SSI, LI)와 시간강수량의 변화를 비교한 것이다. Figure 8a는 2011년 7월 27일의 KI, SSI, LI의 시간에 따른 변화를 각각 나타낸 것으로, SSI는 강수가 시작(−1.242 K)되면서 감소하기 시작하여 강수가 증대되는 시점에 다시 증가하는 것으로 나타났으며, 반대로 KI는 30이상의 값이 나타났으며, 강수가 시작되면서 증가되다가 강수가 강해지는 시간대에 감소하는 것으로 나타났다. LI는 강수가 시작되는 시점에 상대적으로 높은 값으로 나타났으나, 시간이 지날수록 낮아지는 특성을 보였다. Figure 8b는 2010년 9월 21일 집중호우 사례에서의 KI, SSI, LI의 시간에 따른 변화를 나타낸 것으로, KI는 강수전에 가장 높게 나타났으나 지속적으로 감소하는 경향을 보였으며, SSI와 LI는 집중호우 발생되기 전에 증가하기 시작하여 지속적으로 증가하는 경향을 보였다. Figure 8c는 2013년 9월 13일 사례의 불안정 지수의 변화를 나타낸 것으로, KI와 SSI는 집중호우가 발생하기 전에 감소되는 특성이 있었으며, LI는 강수 시작과 함께 급격히 감소한 후 집중호우 발생 전에 서서히 증가하는 특성이 있었다. 우리나라에서 발생된 여름철 대부분의 호우는 KI 값이 30 K 이상(KMA, 2011)에서 나타난 것처럼 본 사례에서도 집중호우 발생 시점에서 KI 값은 30 K 이상으로 나타났다.
이러한 불안정지수는 계절이나 기상조건에 맞는 적절한 지수 선택이 선행되어야 하지만, 분석에 사용된 불안정 지수들이 강수량의 변화에 따라 증감하는 등의 변화 특성은 보였으나, 선별된 사례에 대해 일괄적인 증가나 감소 등의 변화 특성을 나타내지는 않았다. 불안정 지수는 집중호우를 예측하는 보조지표로서 활용할 수 있을 것으로 예상되지만, 강수시스템이나 기상 조건에 따라 변동 특성이 다르게 나타났다. 다시 말해, 불안정 지수만을 이용한 집중호우 예측은 한계가 있을 것으로 예상되며, 적절한 불안정 지수의 선택과 분석이 요구되어지고, 다른 예측변수와의 접목을 통하여 집중호우 예측에 활용할 필요가 있다.
4.6 헬리시티(Storm-Relative Helicity)
Storm-Relative Helicity (SRH)는 스톰의 저기압성 상승 회전(cyclonic updraft rotation)의 가능성을 수치화한 것으로, 지상에서 1 km 혹은 3 km까지 계산된다. 슈퍼셀(supercell)과 토네이도(tornado)의 예보 도구로서 유용하며, SRH의 값이 150 m2 s−2 이상일 경우 강한 대류성 스톰이 발생할 가능성이 높다고 분석한다(Davies-Jones, 1984; Davies-Jones et al., 1990; Rasmussen and Blanchard, 1998; Clark et al., 2013). 많은 연구에서 저층 SRH가 토네이도의 잠재성을 나타내는 좋은 도구이며, 위험기상 예측을 위한 중요한 예후 변수(prognostic variable)로서 활용 가능함(Leftwich, 1990; Rasmussen and Blanchard, 1998; Thompson et al., 2003)을 밝혔다.
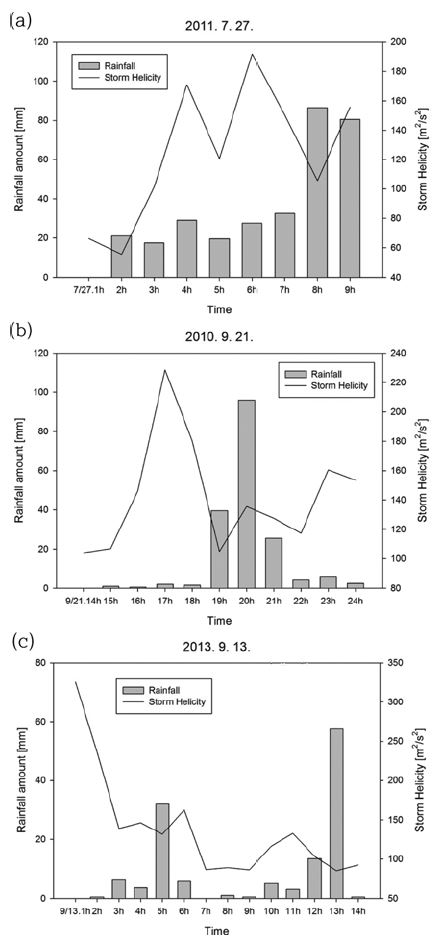
Figure 9는 세 사례에서의 시간에 따른 SRH 변화를 나타낸 것으로, case 1에서는 SRH 최대값이 0600 LST에 191.9 m2 s−2으로 나타났으며, case 2에서는 1700 LST에 228.6 m2 s−2, case 3에서는 강수가 시작되는 0100 LST에 325.6 m2 s−2의 값이 나타났다. 세 사례 모두 집중호우가 발생하기 전에 대류성 스톰이 발생 가능성이 높은 150 m2 s−2 이상의 값을 보였고, 집중호우가 발생한 시점에서는 150 m2 s−2 이하의 값으로 나타났다. SRH의 값은 집중호우가 발생하기 전에 증가(혹은 최대값)하다가 집중호우가 발생하기 전에 급격히 감소되는 경향이 있었다. 또한 집중호우 발생 전에 상대적으로 강한 SRH가 몇 시간 지속되어 나타남으로서 상승류를 발달시키고 뇌우 발달을 가속화시킨 것으로 생각된다. 따라서 집중호우 발생 전에 높은 SRH가 몇 시간 지속되면 스톰 발생이나 집중호우 시의 전조현상으로 파악할 수 있으며, 집중호우 사전 예측에 활용할 수 있을 것이다. 따라서, 스톰이나 위험기상의 시공간적 변동성을 짐작할 수 있는 SRH의 정확한 추정이 선행되어야 하며, 다른 예측 변수들과의 조합을 통하여 집중호우 발생지역 등을 예측할 수 있을 것으로 기대된다.
4.7 결과 및 토의
이상으로 선별된 세 사례에서 추출된 변수를 이용하여 집중호우시의 특성을 분석하였으며, 사례 기간동안 각 변수들의 최소값, 최대값, 그리고 최대강수량이 나타난 시점(Time of Max. hourly rainfall amount: TMHR)에서의 값을 Table 2에 나타내었다.
구름 두께는 각 사례별로 집중호우 발생 시점에 11.54 km, 4.57 km, 9.41 km의 구름 두께를 가지는 것으로 나타났으며, 최소 4.57 km 이상의 구름 두께를 가지는 구름에서 집중호우가 발생되었다. 누적수함량은 최소 0.0041 mg m−3에서 최대 12.8 mg m−3의 범위로 나타났으며, 집중호우 발생시점에는 대부분 사례에서 낮아짐을 확인하였다. 즉, 누적수함량은 강수 시작 시점에 증가하기 시작하여 집중호우가 발생되기 몇 시간 전부터 급격히 감소하는 것으로 나타났다. 양의 부력에너지는 case 1과 case 3에서는 강수시작 시점부터 증가하기 시작하여 1,000 J kg−1 이상의 값으로 나타난 후 집중호우 발생시점(925.84 J kg−1와 615.81 J kg−1)에 감소하는 것으로 나타났으며, case 2에서는 양의부력에너지가 거의 나타나지 않았다. 열적이류(temperature advection과 potential temperature advection)는 case 1과 case 2에서는 강수시작 시점부터 증가하기 시작하여 집중호우 발생시점에 거의 최대값이 나타났으나, case 3에서는 집중호우 발생시점에 가장 낮은 값(−0.09 K s−1와 −0.08 K s−1)이 나타났다. 불안정지수는 변동성이 다양하게 나타났으며, KI 값은 집중호우 발생시점에 30 이상의 값으로 나타났다. SSI는 case 1과 case 2에서는 집중호우 발생시점에 증가하는 경향을, case 3에서는 감소하는 것으로 나타났다. LI는 case 1에서는 감소하는 것으로 나타났으며, case 2와 case 3에서는 집중호우 발생시점에 증가하는 것으로 나타났다. SRH는 최소 55.52에서 최대 325.67의 값으로 분포하였으며, 집중호우 발생 전에 증가하다가 집중호우 발생시점에 감소하는 것으로 나타났다.
결과적으로, 분석에 사용된 대부분의 변수들이 집중호우 발생시점 전에 변화 경향이나 변동 특성이 있는 것으로 나타났으며, 기존에 사용되던 CAPE, 불안정지수, SRH도 집중호우 유형이나 사례에 따라 변화경향이나 값의 변동이 다양하게 나타남으로 인해 이를 일괄적으로 적용하는데는 세밀한 검토가 필요할 것이다. 추가적으로 구름 두께, 누적수함량 변화, 열적이류 등은 집중호우 발생과 부합되는 변동 경향이나 특성이 나타남에 따라 집중호우 예측을 위한 변수로서 활용 가능성이 있을 것으로 생각된다.
5. 결 론
집중호우를 사전에 예측할 수 있는 가능성을 알아보기 위하여 고해상도의 KLAPS 재분석 자료에서 산출되는 각종 변수를 추출하여 정량적인 분석을 수행하였다. 집중호우 유형이 서로 다른 세 사례(라인형태의 deep convective system, 전선형 shallow convective system, 국지성 대류시스템)에 대한 분석을 수행하였다.
집중호우가 내리는 지역은 최소 약 4.5 km 이상의 대류형 구름이 존재하였으며, 10 km 이상의 구름두께를 가지는 대류형 구름에서 발생하였다. 누적수함량분포는 집중호우 발생 전에 최대값이 나타난 후 급격히 감소하였으며, 열적 이류(temperature and potential temperature advection)의 유입이 활발하며, 양의 부력 에너지의 증가에 따른 대류불안정이 가속화되고, 각종 지수(K-Index, Showalter Stability Index, Total Totals, Lifted Index 등)가 강수량의 변화에 따라 변동되는 특징이 있음을 확인하였다. 또한 SRH는 집중호우 발생 전에 대류성 스톰의 발생 가능성이 높은 150 m2 s−2 이상의 값을 보였고, 급격히 감소되는 경향이 있었다. 대부분의 변수들이 집중호우 발생 전에 급격한 증감이나 변화 특성이 나타났다. 이러한 변수들의 급격한 증감이나 변화 양상은 집중호우 발생시의 주변조건이나 기상조건과 부합되어 나타나는 것으로, 이러한 특징을 활용하면 집중호우를 사전에 예측 혹은 진단할 수 있는 변수로서 활용할 수 있을 것이다. 또한 세 사례의 분석 결과, 집중호우 유형에 따라 CAPE, 불안정 지수, SRH 등 예측변수의 변화가 다양하게 나타남으로 인해 이에 대한 세밀한 분석이 필요할 것으로 생각되고, 집중호우 유형이나 기상 조건 등에 맞는 적절한 활용이 요구되어진다.
3차원 격자 자료를 생산하는 수치모델의 결과물을 활용한 집중호우 사전 예측은 일반적으로 사용되는 집중호우 예측변수(CAPE, BRN, wind shear 등)와 더불어 추가적으로 여러 예측변수들의 접목을 통해 예측성을 더 향상시킬 수 있을 것이다. 아울러 변수들의 증감이나 변화량 등을 격자 단위로 실시간 모니터링함으로써 집중호우 발생지역 등에 대한 보다 정확한 정보를 획득할 수 있을 것으로 기대된다. 집중호우와 연관된 추가적인 정보를 기반으로 집중호우의 강도나 발생지역 등을 예측하는 데 더 나은 결과를 보여줄 수 있을 것이다.
하지만, 본 연구에서 선별된 사례들의 유형이나 발생 기작들이 서로 달라서 분석 결과를 모든 집중호우 사례에 적용하기에는 아직 무리가 있지만, 수치모델의 결과물과 같은 3차원 자료에서 생산되는 변수의 비교 분석을 통하여 일반적인 예측변수와 더불어 추가적인 다른 예측변수를 집중호우 예측변수로서 활용할 수 있는 가능성을 확인한 것에 큰 의미가 있다. 향후 보다 다양한 사례에서의 정량적인 값들의 산출 및 분석을 통하여 예측변수들의 임계값(threshold) 등을 일반화함으로서 집중호우 예측성을 향상시키도록 할 예정이다.
Acknowledgments
본 연구는 기상청 차세대도시농림융합스마트기상서비스개발(WISE) 사업의 지원으로 수행되었습니다(KMIPA-2012-0001-1).
REFERENCES
-
Clark, A. J., J. Gao, P. T. Marsh, T. Smith, J. S. Kain, J. Correia Jr., M. Xue, and F. Kong, (2013), Tornado path length forecasts from 2010 to 2011 using ensemble updraft helicity, Wea. Forecasting, 28, p387-407.
[https://doi.org/10.1175/WAF-D-12-00038.1]

-
Davies-Jones, R., (1984), Streamwise vorticity: The origin of updraft rotation in supercell storms, J. Atmos. Sci., 41, p2991-3006.
[https://doi.org/10.1175/1520-0469(1984)041<2991:SVTOOU>2.0.CO;2]

- Davies-Jones, R., D. W. Burgess, and M. Foster, (1990), Test of helicity as a forecast parameter, Preprints, 16th Conf. on Severe Local Storms, Kananaskis Park, AB, Canada, p588-592.
- Djuric, D., (1994), Weather Analysis, Prentice-Hall Inc., p304.
-
Doswell III, C. A., and E. N. Rasmussen, (1994), The effect of neglecting the virtual temperature correction on CAPE calculations, Wea. Forecasting, 9, p625-629.
[https://doi.org/10.1175/1520-0434(1994)009<0625:TEONTV>2.0.CO;2]

-
Edwards, R., and R. L. Thompson, (1998), Nationwide comparison of hail size with WSR-88D vertically integrated liquid water (VIL) and derived thermodynamic sounding data, Wea. Forecasting, 13, p277-285.
[https://doi.org/10.1175/1520-0434(1998)013<0277:NCOHSW>2.0.CO;2]

- George, J. J., (1960), Weather Forecasting for Aeronautics, Academic Press, p673.
-
Greene, D. R., and R. A. Clark, (1972), Vertically integrated liquid water - a new analysis tool, Mon. Wea. Rev., 100, p548-552.
[https://doi.org/10.1175/1520-0493(1972)100<0548:VILWNA>2.3.CO;2]

- Huschke, R. E., (1970), Cloud height, In T. S. Glickman, 2nd Ed., Glossary of Meteorology, American Meteorological Society, Retrieved from August 24, 2013.
-
Jang, M., C. H. You, J. B. Jee, S. H. Park, S. I. Kim, and Y. J. Choi, (2016), Three-dimensional analysis of heavy rainfall using KLAPS re-analysis data, Atmosphere, 26, p97-109, (in Korean with English abstract).
[https://doi.org/10.14191/Atmos.2016.26.1.097]

-
Jung, S. P., S. R. In, H. W. Kim, J. K. Sim, S. O. Han, and B. C. Choi, (2015), Classification of atmospheric vertical environment associated with heavy rainfall using long-term radiosonde observational data, 1997~2013, Atmosphere, 25, p611-622, (in Korean with English abstract).
[https://doi.org/10.14191/Atmos.2015.25.4.611]

- Kato, T., (1998), Numerical simulation of the band-shaped torrential rain observed over southern Kyushu, Japan on 1 August 1993, J. Meteor. Soc. Japan, 76, p97-123.
-
Kim, D. W., Y. H. Kim, K. H. Kim, S. S. Shin, D. K. Kim, Y. J. Hwang, J. I. Park, D. Y. Choi, and Y. H. Lee, (2012), Atmospheric vertical structure of heavy rainfall system during the 2010 summer intensive observation period over Seoul metropolitan area, J. Korean Earth Sci., 33, p148-161.
[https://doi.org/10.5467/JKESS.2012.33.2.148]

- Kim, K. H., Y. H. Kim, and D. E. Chang, (2009), The analysis of Changma structure using radiosonde observational data from KEOP-2007: Part II. The dynamic and thermodynamic characteristics of Changma in 2007, Atmosphere, 19, p297-307, (in Korean with English abstract).
- Kim, Y. C., and S. J. Ham, (2009), Heavy rainfall prediction using convective instability index, J. Korean Soc. Aviat. Aeronaut., 17, p17-23.
- KMA, (2011), Forecasting techniques caught in the hand, Instability Index, No. 3 p2, (in Korean).
-
Kwon, T. Y., J. S. Kim, and B. G. Kim, (2013), Comparison of the properties of Yeongdong and Yeongseo heavy rain, Atmosphere, 23, p245-264, (in Korean with English abstract).
[https://doi.org/10.14191/Atmos.2013.23.3.245]

- Leftwich, P. W., (1990), On the use of helicity in operational assessment of severe local storm potential, Preprints, 16th Conf. on Severe Local Storms, Kananaskis Park, AB, Canada, p269-274.
- Maddox, R. A., (1979), A methodology for forecasting heavy convective precipitation and flash flooding, Nat. Wea. Dig., 4, p30-42.
- NIMS, (2009), Development of very short-range prediction system for severe weather, National Institute of Meteorological Sciences, p277, (in Korean).
- NIMS, (2012), Improvement of prediction skills in very short, short and mid-term for severe weather (IV), National Institute of Meteorological Sciences, p86, (in Korean).
- Park, C. G., and T. Y. Lee, (2008), Structure of mesoscale heavy precipitation systems originated from the changma front, Atmosphere, 18, p317-338, (in Korean with English abstract).
-
Rasmussen, E. N., and D. O. Blanchard, (1998), A baseline climatology of sounding-derived supercell and tornado forecast parameters, Wea. Forecasting, 13, p1148-1164.
[https://doi.org/10.1175/1520-0434(1998)013<1148:ABCOSD>2.0.CO;2]

-
Richardson, Y. P., K. K. Droegemeier, and R. P. Davies-Jones, (2007), The influence of horizontal environmental variability on numerically simulated convective storms. Part I: Variations in vertical shear, Mon. Wea. Rev., 135, p3429-3455.
[https://doi.org/10.1175/MWR3463.1]

- Showalter, A. K., (1953), A stability index for thunderstorm forecasting, Bull. Amer. Meteor. Soc., 34, p250-252.
- Spellman, F. R., (2013), The handbook of Meteorology, Scarecrow Press, p33.
-
Thompson, R. L., R. Edwards, J. A. Hart, K. L. Elmore, and P. Markowski, (2003), Close proximity soundings within supercell environments obtained from the rapid update cycle, Wea. Forecasting, 18, p1243-1261.
[https://doi.org/10.1175/1520-0434(2003)018<1243:CPSWSE>2.0.CO;2]

-
Thompson, R. L., C. M. Mead, and R. Edwards, (2007), Effective storm-relative helicity and bulk shear in supercell thunderstorm environments, Wea. Forecasting, 22, p102-115.
[https://doi.org/10.1175/WAF969.1]