다중 지역기후모델로부터 모의된 월 기온자료를 이용한 다중선형회귀모형들의 예측성능 비교
Abstract
In this study, we investigated the prediction skills of four multiple linear regression methods for monthly air temperature over South Korea. We used simulation results from four regional climate models (RegCM4, SNURCM, WRF, and YSURSM) driven by two boundary conditions (NCEP/DOE Reanalysis 2 and ERA-Interim). We selected 15 years (1989~2003) as the training period and the last 5 years (2004~2008) as validation period. The four regression methods used in this study are as follows: 1) Homogeneous Multiple linear Regression (HMR), 2) Homogeneous Multiple linear Regression constraining the regression coefficients to be nonnegative (HMR+), 3) non-homogeneous multiple linear regression (EMOS; Ensemble Model Output Statistics), 4) EMOS with positive coefficients (EMOS+). It is same method as the third method except for constraining the coefficients to be nonnegative. The four regression methods showed similar prediction skills for the monthly air temperature over South Korea. However, the prediction skills of regression methods which don’t constrain regression coefficients to be nonnegative are clearly impacted by the existence of outliers. Among the four multiple linear regression methods, HMR+ and EMOS+ methods showed the best skill during the validation period. HMR+ and EMOS+ methods showed a very similar performance in terms of the MAE and RMSE. Therefore, we recommend the HMR+ as the best method because of ease of development and applications.
Keywords:
Ensemble forecasting, multiple linear regression, regional climate model1. 서 론
인위적 요인에 의한 온실기체의 증가로 지구온난화가 진행됨에 따라 폭염, 집중호우 등과 같은 극한기후 현상의 빈도 및 강도가 증가되고 있음을 많은 선행연구들에서 보였다(Meehl et al., 2000a; Chu and Zhao, 2004; Gemmer et al., 2011; Yun et al., 2012; IPCC, 2014). 지구온난화와 관련된 상세 기후변화정보에 대한 관심이 높아지고 있는 추세이며 많은 선진국들은 기후변화가 미치는 영향을 파악하기 위해 다양한 전지구기후모델(General Circulation Model; GCM) 및 지역기후모델(Regional Climate Model; RCM)을 이용하여 신뢰성 있는 현재 기후와 미래 기후변화 정보를 생산하기 위해 노력 중에 있다(Gates, 1992; Meehl et al., 2000b; Fu et al., 2005; Myoung et al., 2012; Lee et al., 2014). 하지만 전지구기후모델은 계산의 용이성을 위해 물리과정이 단순화되어 있으며 수평해상도가 수 백 km에 이른다. 따라서 지역 또는 국지적으로 발생하는 기상현상을 현실적으로 모의하는데 한계가 있을 뿐만 아니라 사용된 물리모수화과정에 따라 불확실성이 존재한다(Giorgi et al., 2001; Mearns et al., 2001; Choi et al., 2011; Lee et al., 2014).
이러한 전지구기후모델의 단점을 보완하기 위해 역학적 규모축소 방안인 지역기후모델에 대한 연구가 1990년대 이후부터 활발하게 이루어지고 있다(e.g., Giorgi et al., 1993a, b; Grell et al., 1994; Juang et al., 1997; Suh and Lee 2004). 일반적으로 지면, 지형정보 등과 같은 지역기후인자들이 적절하게 처방된다면 지역기후모델은 전지구기후모델보다 상세하고 신뢰성있는 지역기후정보를 생산할 수 있다. 하지만 지역기후모델 역시 입력자료의 초기 조건, 측면경계조건, 모델의 수평해상도와 물리과정 등에 영향을 받기 때문에 결과에 불확실성이 존재한다(Kalnay, 2003; Choi et al., 2011; Feng et al., 2011; Cui et al., 2012; Kim and Suh, 2013). 따라서 이러한 모델들의 불확실성을 파악하기 위해 CORDEX (Coordinated Regional climate Downscaling Experiment), 유럽의 PRUDENCE (Prediction of Regional Scenarios and Uncertainties for Defining European Climate Change Risk and Effects)와 Ensembles 등과 같은 국제적인 프로젝트가 수행되어왔다(Christensen and Christensen, 2007; Giorgi et al., 2009; van der Linden and Mitchell, 2009). 특히, 우리나라에서도 기상청 주관 하에 공주대, 서울대, 연세대가 서로 다른 4개의 지역기후모델(RegCM4, SNURCM, YSURSM, WRF)에 HadGEM2-AO (Hadly Centre Global Environment Model, version2) 전구모델자료를 경계조건으로 처방하여 CORDEX 동아시아 영역에 대한 상세 지역기후정보를 생산한 바 있다(Choi et al., 2011; Myoung et al., 2012).
수문과 농업 등 여러 응용분야에서의 활용과 보다 정확한 미래 기후변화정보를 생산하기 위해 기후모델의 불확실성을 감소시킬 필요성이 있다. 따라서 기후모델의 불확실성을 감소시키기 위해 모델의 물리과정 개선 및 대기-해양모델 결합 등의 지속적인 모델의 개선이 요구된다(Yun et al., 2003). 하지만 기후모델들이 갖는 한계를 단기적으로 해결하기 어렵기 때문에 모델의 불확실성을 감소시키기 위한 다양한 통계적 후처리 방법들에 대한 연구가 진행되어왔다(e.g. bias correction and ensemble forecasting).
Krishnamurti et al. (1999)은 다중선형회귀에 기반한 앙상블 기법(superensemble)을 이용하여 850 hPa 남북바람의 계절 예측을 수행하였다. 이로부터 앙상블 기법이 각 앙상블 멤버보다 뛰어난 예측성능을 보임을 제시하였다. Peng et al. (2002)은 MME (Multi-Model Ensemble)방법과 다중선형회귀를 이용한 가중평균 방법을 AGCM (Atmospheric General Circulation Model)이 모의한 500 hPa 지위고도에 적용하여 계절예측을 수행하였다. 또한 Suh et al. (2012)은 본 연구와 같은 월 기온자료를 이용하여 훈련기간의 각 모델 별 예측성능에 기반한 새로운 앙상블기법을 개발하였으며 가중평균방법이 동일 가중치 방법과 각 모델보다 향상된 예측성능을 보이는 것을 확인하였다. 하지만 결정론적 앙상블 방법은 사용된 모델 또는 통계적 기법에 따라 다른 예측성능을 보인다는 한계가 존재한다(Christensen et al., 2010). 이러한 결정론적 앙상블 기법의 한계를 극복하기 위해 확률론적 앙상블 기법에 대한 연구가 진행되었다. Raftery et al. (2005)은 BMA(Bayesian Model Averaging) 기법을 기온 및 해면기압에 적용하여 결정론적 및 확률론적 예측을 시도하였다. 국내에서도 Kim and Suh (2013)가 본 연구에서 쓰인 동일한 월 기온자료에 BMA 기법을 적용하여 확률예측의 가능성을 제시하였다. 특히, Gneiting et al. (2005)은 잔차를 이분산으로 가정한 다중선형회귀모형을 통해 예측확률밀도함수와 누적분포함수를 구하여 기온 및 해면기압에 대해 확률론적 앙상블 예측을 하였다. 또한 앙상블 스무싱 기법과 변환 기법(Wilks, 2002) 등을 통해 강수와 같이 정규분포를 따르지 않는 기상변수에 대한 적용 가능성을 제시하였다.
기온자료에 대한 적용의 편리성을 고려하여, 본 연구에서는 여러 통계적 후처리 방법 중 결정론적 예측 및 확률 예측이 가능한 Ensemble Model Output Statistics 방법(Gneiting et al., 2005)을 포함한 네 가지 다중선형회귀모형을 선정하였다. 선정된 네 가지 다중선형회귀모형들의 예측성능 비교를 통해 남한의 월 평균 기온 예측에 적합한 모형을 찾아 보다 신뢰성 있는 남한의 월 평균 기온 정보를 제공하고자 하였다. 다음절에서는 본 연구에서 사용된 지역기후모델과 실험설계를 설명하고, 네 가지 다중선형회귀모형에 대한 설명과 예측 성능을 분석한 후 끝으로 연구 결과를 요약하였다.
2. 모델 및 실험설계
본 연구에서는 2개의 경계조건(NCEP-DOE Reanalysis 2; R2와 ERA-interim; ERA)을 처방한 4개의 지역기후모델(RegCM4, YSURSM, SNURCM과 WRF)을 이용하여 8개의 앙상블 멤버를 구성하였다. ICTP(International Centre for Theoretical Physics)에서 개발한 RegCM4는 이전 버전인 RegCM3와 비교하였을 때, 새로운 모수화 방안(CLM land surface process scheme, UW-PBL scheme, and diurnal SST scheme)이 추가되었으며 기존의 경계층 방안(Holtslag PBL) 및 복사전달 방안(radiative transfer package)에 대한 수정이 이루어졌다. RegCM4에 대한 보다 상세한 사항은 Giorgi et al. (2012)에 기술되어 있다. YSURSM은 NCEP 계절예보모델(Kanamitsu et al., 2002)과 RSM (Regional Spectral Model, Juang et al., 1997)에 기반을 둔 모델로, 전구 및 지역규모의 예보를 위해 연세대학교에서 개발하였다(Hong et al., 2013). SNURCM은 NCAR (Pennsylvania State University-National Center for Atmospheric Research)의 MM5 (fifth-generation mesoscale model)을 기반으로 개발된 모델이며 서울대학교에서 동아시아와 한반도 기후 모의 성능을 향상시키기 위하여 스펙트럴 넛징(spectral nudging) 기법, 행성경계층방안 등을 개선한 모델이다(Choi et al., 2011). 또한 NCAR에서 현업 운용과 연구에의 활용을 고려하여 개발한 WRF는 가장 널리 쓰이는 중규모 모델로 다양한 물리 모수화 과정과 역학과정들을 포함하고 있다(Skamarock et al., 2008; Choi et al., 2011).
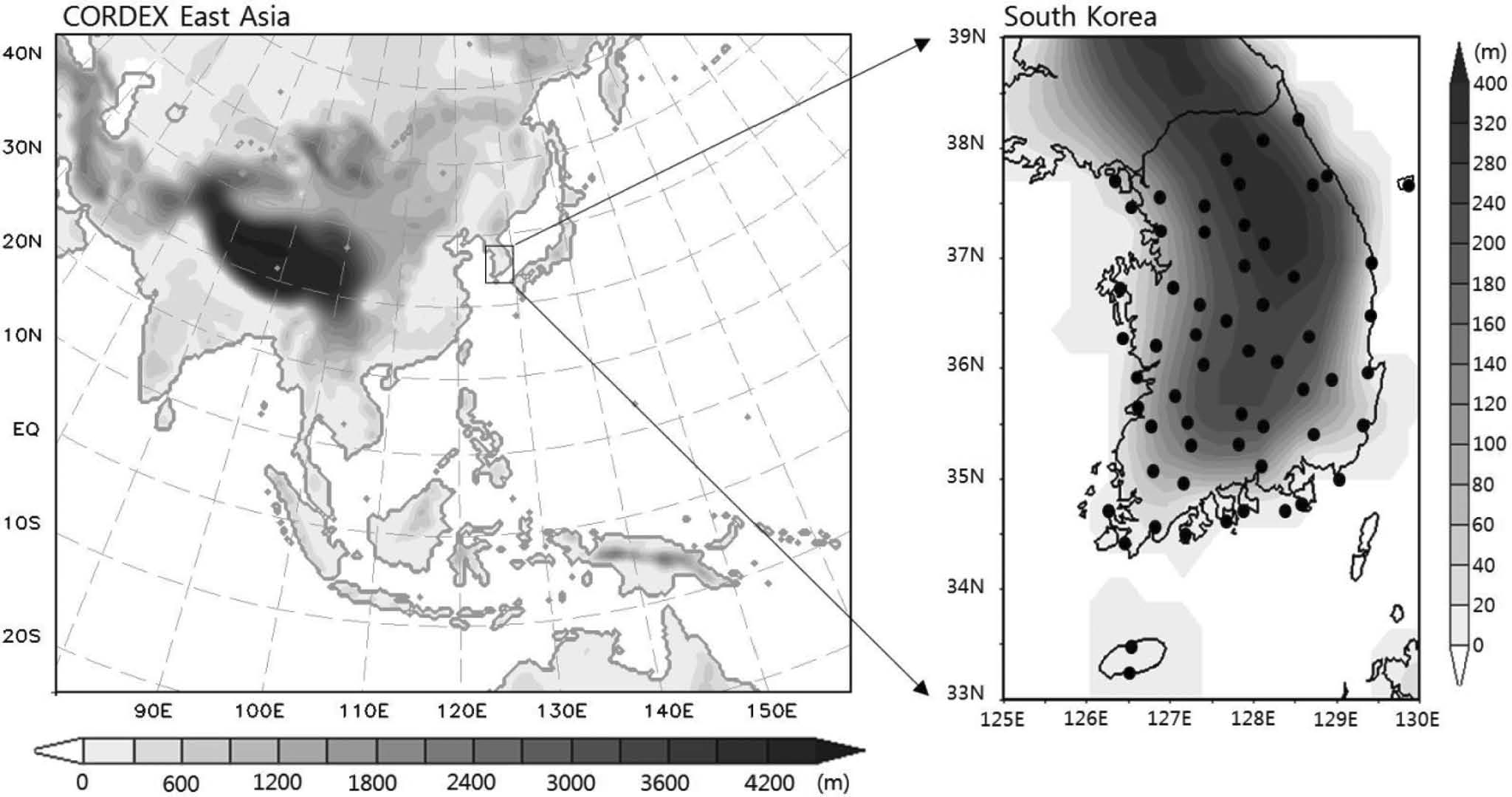
Topography (m) and domain used for RCM simulations over the CORDEX East Asia. The black dots indicate observing stations being operated by KMA (Korea Meteorological Administration).
실험에서 사용된 모의영역은 서태평양, 벵갈만과 아시아 대부분 지역을 포함하는 CORDEX 동아시아 영역(Fig. 1)이며 모델 결과의 상호비교를 위해 모든 모델들의 도메인 중심(35N, 105E)과 수평 해상도(50 km)를 통일하였다. 또한, 장기 적분에 있어 모델의 계통오차(systematic bias)를 최소화 하기 위한 방안으로 스펙트럴 넛징 기법을 모든 모델에 적용하였다. 각 모델에서 사용된 물리 모수화 방안 등에 대한 세부사항은 Table 1에 나타내었으며 이는 Suh et al. (2012)과 Kim and Suh (2013)에서 사용된 것과 동일하다. 모델의 모의기간은 총 20년(1989~2008)이며 그 중 앞의 15년(1989~2003)은 훈련기간으로, 마지막 5년(2004~2008)을 검증기간으로 설정하였다.
모델자료와 비교 및 검증을 위한 관측자료로써 기상청에서 제공받은 59개 지점의 ASOS (Automated Synoptic Observing System) 기온 자료를 사용하였으며 관측자료와 모델자료간의 공간 일치를 위해 이중 선형보간법(bilinear interpolation)을 이용하여 모델자료를 관측지점의 위경도 값으로 재산출한 후 분석을 수행하였다.
3. 연구방법
이 장에서는 다중선형회귀모형의 예측성능 분석을 위한 평가 척도, 잔차를 등분산으로 가정한 다중선형회귀방법, 그리고 앙상블 spread-skill 관계성이 고려된 잔차를 이분산으로 가정한 다중선형회귀방법에 대해 설명하고자 한다.
3.1 평가 척도
본 연구에서는 다중선형회귀모형의 예측성능 평가를 위해 절대평균오차(Mean Absolute Error; MAE), 평균제곱근오차(Root Mean Squared Error; RMSE)와CRPS (Continuous Ranked Probability Score)를 사용하였다.
관측치를 yi, 모델의 예측치를 fi라고 할 때, 절대평균오차는 식(1), 평균제곱근오차는 식(2)와 같이 주어지며 이 두 가지 척도는 관측과 같은 단위를 가지기 때문에 해석이 용이하다는 장점이 있다.
| (1) |
| (2) |
CRPS란 Brier score의 합으로 해석할 수 있으며(Hersbach, 2000) CRPS의 값이 작을수록 예측치와 관측치의 누적분포함수가 유사하다고 할 수 있다. 모델예측치의 누적분포함수를 Fif, 관측치의 누적분포함수를 Fio라고 할 때, crps는 식(3)과 같이 표현된다.
| (3) |
기온이 평균이 μ이고 표준편차가 σ인 정규분포를 따른다고 할 때, 식(3)을 식(4)와 같이 표현할 수 있다(Gneiting et al., 2005).
| (4) |
여기서 Φ((y − μ)/σ)와 ϕ((y − μ)/σ)는 각각 평균이 0, 표준편차가 1로 표준화된 정규분포의 누적분포함수와 확률밀도함수이다. 모든 자료에 대한 crps의 평균은 식(5)와 같이 표현된다.
| (5) |
3.2 다중선형회귀와 EMOS (Ensemble Model Output Statistics)
임의의 예측치 y에 대한 행렬이 식(6)과 같이 주어졌을 때, 다중선형회귀방정식은 식(7)과 같이 표현될 수 있다. 여기서 β0, β1, …, βk는 회귀계수이며 ε은 잔차로써 평균이 0이고 표준편차가 σ인 정규분포를 따른다고 가정한다. 일반적으로 회귀계수는 최소자승법을 이용하여 추정되며 그 추정식은 식(8)과 같다.
| (6) |
| (7) |
| (8) |
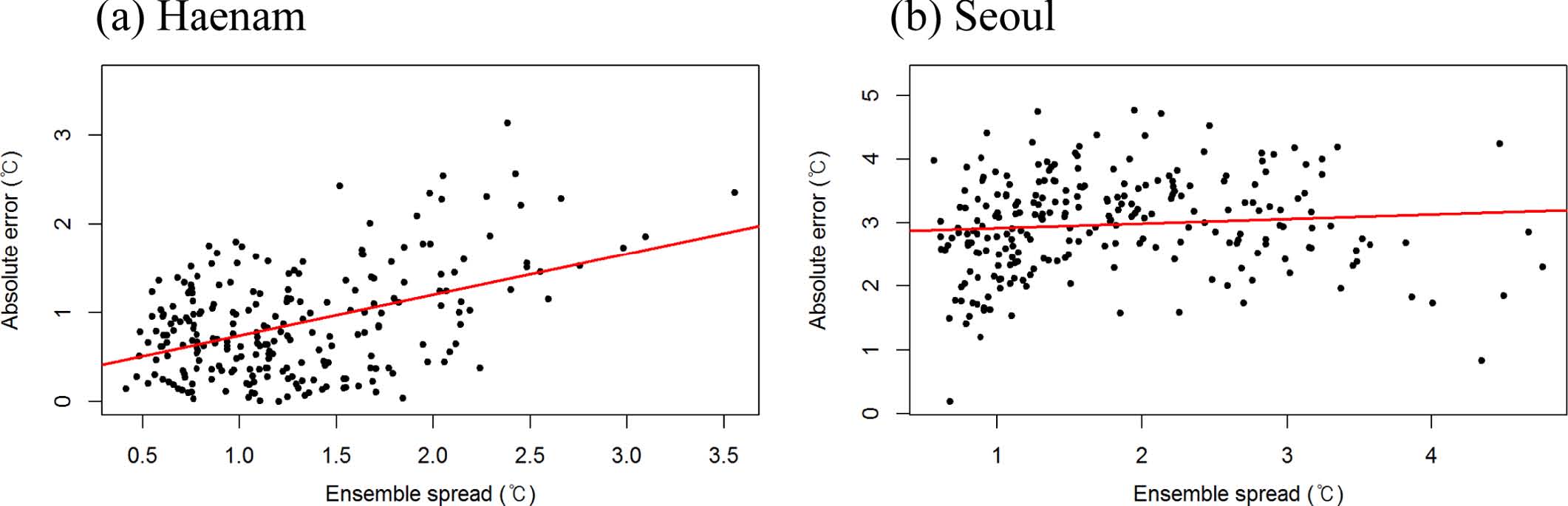
일반적인 선형회귀 이론에서 예측확률밀도함수와 예측누적분포함수를 계산하는 것은 어려운 일이 아니다. 예측확률밀도함수는 평균이 다중선형회귀를 통해 산출된 예측치, 분산이 예측 오차의 자승이 되는 정규분포를 갖는다. 이러한 방법은 모델의 편의를 보정해주고 변동오차를 고려할 수 있다. 하지만 일반적인 다중선형회귀모형은 Fig. 2(a)와 같이 앙상블 분산과 절대 오차 사이에 선형적 관계가 존재할 때 적용하기에 적합하지 않다는 한계가 있다. 따라서 Gneiting et al. (2005)은 이러한 문제를 해결하기 위해 식(9)와 같이 예측치의 분산이 앙상블 분산에 선형적으로 종속되도록 이분산으로 설정하였다.
| (9) |
여기서 Si2는 i번째 앙상블 분산이며 c와 d는 음수가 아닌 분산 계수이다. 식(7)과 식(9)를 결합하여 정규분포를 따르는 예측 분포를 다음과 같이 표현할 수 있다. 여기서 평균은 다중선형회귀를 통해 산출된 예측치이며 분산은 앙상블 분산에 선형적으로 비례하도록 하였다. 분산계수 c와 d는 앙상블 분산과 앙상블 평균예측치 성능의 관점에서 해석될 수 있다. 모든 조건이 동일하다고 할 때, d의 값이 클수록 앙상블 spreadskill 관계가 강하게 나타나고 있음을 보여준다. 반면 앙상블 spread-skill 관계가 존재하지 않는다면 분산계수 d는 무시될 정도로 작은 값으로 추정이 될 것이다. 이와 같은 경우, 잔차를 등분산으로 가정한 일반적인 다중선형회귀모형과 유사한 결과를 제공한다.
| (10) |
훈련기간의 자료를 사용하여 회귀계수 β0, β1, …, βk, c, d를 추정하기 위해 일반적으로 최대우도추정법(Maximum Likelihood Estimation; MLE)이 널리 쓰이고 있다. 우도함수에 대한 최댓값을 찾는 방법보다 우도함수에 로그를 취하여 최댓값을 찾는 것이 보편적인 방법이며 식(10)에 대한 로그우도함수는 식(11)과 같이 표현된다.
| (11) |
여기서 xi1, xi2, …, xik는 훈련기간에 대한 각 앙상블 멤버의 i번째 예측치이며 Si2는 i번째 예측치들의 분산이다.
또 다른 회귀계수의 추정방법으로 식(4)와 식(5)를 이용하여 CRPS 값을 최소로 만드는 방법이며 계수추정을 위한 식은 다음과 같다(Gneiting et al., 2005).
| (12) |
Zi는 표준화된 예측오차이며 Φ와 ϕ는 각각 표준정규분포의 누적분포함수와 확률밀도함수이다. Gneiting et al. (2005)은 예측치의 분산이 과대 추정되는 경우 최대우도추정법이 최소 CRPS 추정법보다 더 큰 영향을 받는다고 언급하였다. 따라서 본 연구에서는 최소 CRPS 추정법을 사용하여 회귀계수를 추정하였다. 식(12)를 최소화시키는 계수들을 찾기 위해 Broyden-Fletcher-Goldfarb-Shanno 알고리즘(Dai, 2002)을 사용하였다. 하지만 이러한 최적화 알고리즘은 함수의 최대(최소) 값에서 수렴한다는 보장이 없으며 초기값에 민감하게 반응한다는 한계가 존재한다.
다중선형회귀에서 회귀계수들은 다른 앙상블 멤버들에 대한 각 앙상블 멤버들의 전반적인 성능을 반영한다. 하지만 어떤 예측치에 해당되는 회귀계수가 큰 음수 값을 가지게 된다면 예측치가 아주 작게 모의될 가능성이 있다. 또한, 음수의 회귀계수는 가중치로써 해석하기가 어려운 경향이 있다. 따라서 이러한 문제점을 다루기 위해 본 연구에서는 Gneiting et al. (2005)과 같이 회귀계수가 음수일 때, 해당 회귀계수를 0으로 둔 후 모든 회귀계수가 음수가 되지 않을 때까지 재추정하였다. 본 연구에서는 잔차가 등분산인 경우와 이분산인 경우 모두 고려하였으며 잔차가 등분산인 일반적인 다중선형회귀모형을 HMR (Homogeneous Multiple linear Regression), 잔차가 이분산인 다중선형회귀모형을 Gneiting et al. (2005)과 같이 EMOS (Ensemble Model Output Statistics)라고 하였다. 또한, 회귀계수가 음수가 되지 않도록 제약을 둔 방법 중잔차가 등분산인 경우를 HMR+, 이분산인 경우를 EMOS+로 각각 표기하였다.
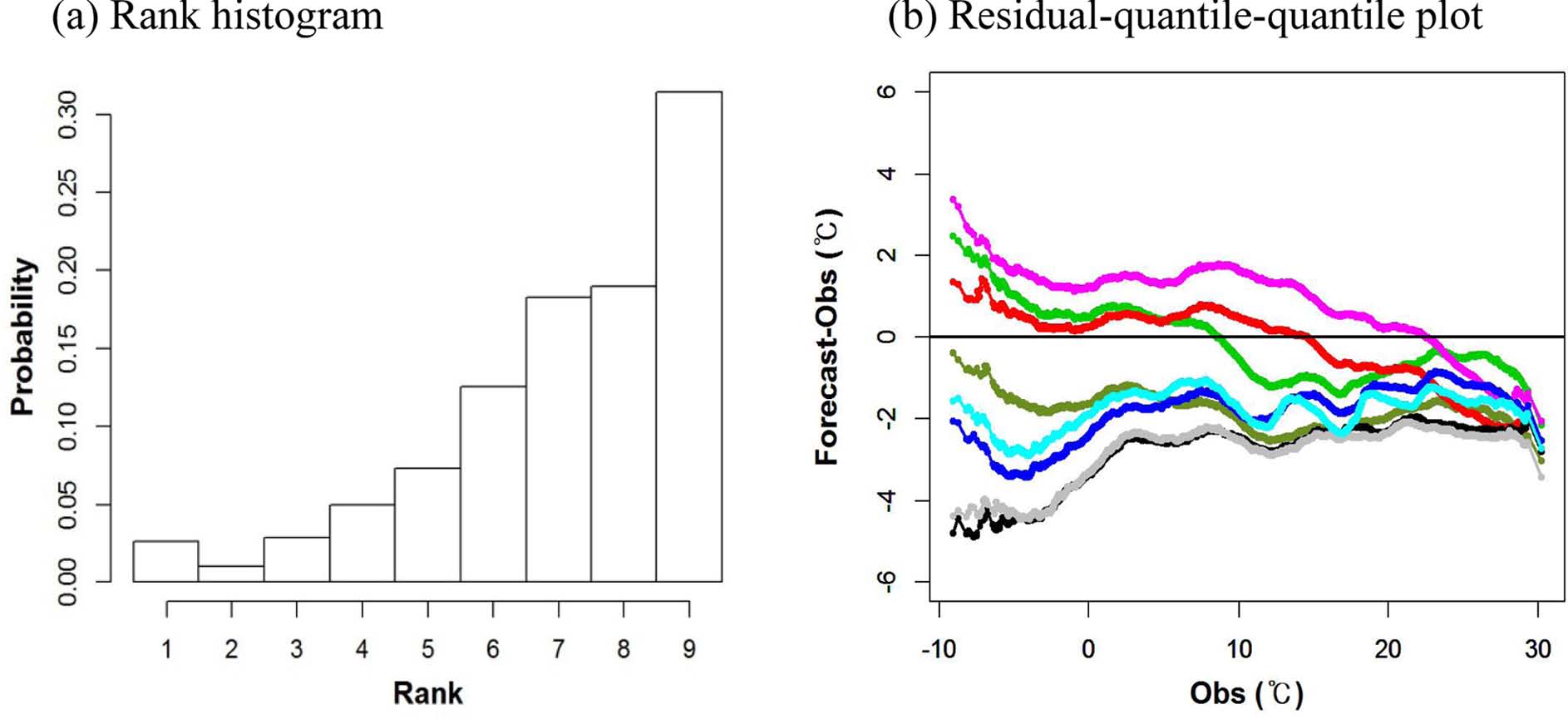
Rank histogram and residual-quantile-quantile plot for eight ensemble forecasts. In the residualquantile- quantile plot, the green, olive, red, light red, black, gray, blue, and light blue lines indicate the ensemble members RCM4_ERA, RCM4_R2, YRSM_ERA, YRSM_ R2, SRCM_ERA, SRCM_R2, WRF_ERA, and WRF_ R2, respectively.
4. 연구결과
4.1 8개 앙상블 멤버의 모의성능 분석
다중선형회귀모형을 적용하기에 앞서 각 모델과 전반적인 모델의 모의수준을 알아보기 위해 순위 히스토그램과 Residual-quantile-quantile (R-Q-Q) 그래프를 사용하였다. 순위 히스토그램은 앙상블 멤버에 대한 관측의 순위를 히스토그램으로 나타낸 것으로 관측과 비교했을 때, 앙상블 멤버들이 어떠한 특징을 가지고 있는지 쉽게 파악할 수 있는 유용한 도구이다(Hamill, 2001). 예를 들어 순위 히스토그램이 균등할 때, 관측과 앙상블 멤버들이 같은 분포라 볼 수 있으며 순위 히스토그램이 U자(역 U자)형을 보일 때, 앙상블 멤버들이 관측보다 해당 변수의 변동성을 과소(과대)하게 모의하는 것을 의미한다. Quantile-quantile 그래프는 앙상블 예보의 신뢰성 평가를 위한 또 다른 도구로써 관측과 이에 상응되는 앙상블 예보의 분위수를 나타낸 것이다(Chandler, 2005; Wilk, 2006). R-Q-Q 그래프는 두 자료의 백분위수 차이를 계산하여 나타낸 것으로 Quantile-quantile 그래프를 45도 시계 방향으로 회전한 결과와 동일하다. R-Q-Q 그래프에서 음(양)의 기울기는 과소(과대)분산을 의미한다(Marzban et al., 2011).
Figure 3은 1989년부터 2008년까지 8개 모델 결과 대한 순위 히스토그램과 R-Q-Q 그래프를 나타낸 것이다. 순위 히스토그램에서 관측의 순위가 오른쪽으로 치우쳐 있으며 히스토그램이 U 자형 모양을 보이고 있다. 따라서 전반적으로 8개 모델은 관측보다 기온을 과소 모의하고 있으며 기온의 변동성 또한 관측보다 작게 모의하고 있다는 것을 알 수 있다. R-Q-Q 그래프에서 YRSM_ERA, YRSM_R2와 RCM4_ERA가 음의 기울기를 보이는 것으로 보아 모델이 기온의 변동성을 관측의 변동성보다 작게 모의하는 것을 알 수 있다. 나머지 5개 모델은 관측의 기온 변동성과 유사하게 모의하고 있으나 관측보다 기온을 약 1~5oC 낮게 모의하는 것을 알 수 있다. 이러한 각 모델들의 특징이 전반적으로 작용하여 위에서 언급한 순위 히스토그램과 같은 특징을 보였다.
4.2 다중선형회귀 결과
본 연구에서는 59개의 기상청 관측 지점에 대해 검증을 수행하였으며 이중선형보간법을 이용하여 모델자료를 관측과 같은 지점의 값으로 재산출한 후 분석하였다. 이상치에 대한 네 가지 다중선형회귀방법의 성능을 알아보기 위해 검증기간에 이상치가 존재하는 천안, 강화 지점과 이상치가 존재하지 않는 서울, 충주 지점을 선정하여 분석하였다.
서울과 충주 지역에 대한 다중선형회귀방법 별 회귀계수와 2007년 1월의 기온 예측치들을 Table 2에 나타내었다. 서울의 경우 HMR+ 방법에서 8개 앙상블 멤버 중 RCM4_R2, YRSM_R2, SRCM_R2와 WRF_ERA가 가중치를 가졌으며 EMOS+ 방법에서는 SRCM_ERA가 약간의 가중치를 가지는 것을 제외하고 HMR+ 방법과 유사하게 나타났다. 또한 분산계수 d가 0인 것으로 보아 앙상블 spread-skill 관계가 존재하지 않는 것을 알 수 있다. 충주의 경우 HMR+ 방법에서 RCM4_R2, RSM_R2, SRCM_ERA, SRCM_ R2와 WRF_ERA가 가중치를 가졌으나 EMOS+ 방법에서는 SRCM_ERA의 가중치가 존재하지 않았다. 분산계수 d가 0.01의 값을 가지는 것으로 보아 충주 지역에서도 앙상블 spread-skill 관계가 거의 존재하지 않음을 보였다. 2007년 1월 월 평균 기온에 대한 다중선형회귀방법 별 예측의 정도를 살펴보았을 때, 서울지역에서는 회귀계수가 음수가 되지 않도록 제약을 두었을 때가 그렇지 않을 때보다 관측치에 가깝게 추정되었음을 알 수 있다. 반면 충주 지역의 경우 회귀계수에 제약을 두지 않은 방법에서 예측치들이 관측과 더 유사함을 보였다.

Summary of coefficients and forecasts (oC) of multiple linear regression for two stations, Seoul and Chungju (in January 2007). The regression coefficients β1, β2, …, β8 correspond to the RCM4_ERA, RCM4_R2, YRSM_ERA, YRSM_R2, SRCM_ERA, SRCM_R2, WRF_ERA, and WRF_R2 forecasts, respectively.

Summary of prediction skills of multiple linear regression methods for temperature in Seoul and Chungju.
Table 3은 서울과 충주 지역의 다중선형회귀방법 별 검증기간에 대한 통계분석을 나타낸 것이다. 서울 지점에서 네 가지 다중선형회귀방법의 편의, 절대평균 오차, 평균제곱근오차와 분산비(variance ratio)가 유사한 값을 보였다. 여기서 분산비란 예측치의 표준편차를 관측치의 표준편차로 나눈 것으로 분산비가 1보다 크(작)다면 예측치의 변동성이 관측의 변동성보다 크(작)다고 할 수 있다. 네 방법 모두 분산비가 약 1의 값을 보여 다중선형회귀를 통해 산출된 예측치의 변동과 관측의 변동이 매우 유사함을 알 수 있다. 충주지점의 경우 회귀계수가 음수가 되지 않도록 제약을 둔 두 방법이 그렇지 않은 방법보다 절대평균오차와 평균제곱근오차가 약 0.03oC 감소하여 소폭 향상된 예측성능을 보였다. 분산비는 네 방법 모두 1의 값을 가져 관측의 변동과 예측치의 변동이 같음을 알 수 있다.
Figure 4는 서울과 충주 지역에서 HMR과 HMR+ 방법의 90% 예측구간을 나타낸 것이다. 여기서 실선은 관측치를 나타내며 점선은 예측확률밀도함수의 90% 예측구간을 나타낸다. 이때, 예측확률밀도함수는 평균이 다중선형회귀식으로부터 산출된 예측치, 분산이 예측 오차의 자승이 되는 정규분포를 따른다. 두 지점 모두 관측값이 예측확률밀도함수의 90% 예측구간에 포함되는 것을 볼 수 있으며 이로부터 다중선형회귀를 통한 두 지점의 확률 예측이 가능하다는 것을 알 수 있다.
천안과 강화 지역에 대한 다중선형회귀방법 별 회귀계수와 2007년 8월의 기온 예측치들을 Table 4에 나타내었다. 천안의 경우 HMR+와 EMOS+ 방법에서 RCM4_R2, YRSM_R2, SRCM_R2와 WRF_ERA가 가중치를 가졌으며 서로 비슷한 값을 보였다. 강화 지점에서는 HMR+와 EMOS+ 방법에서 YRSM_R2, SRCM_R2와 WRF_ERA 3개의 모델이 가중치를 가졌다. 두 지점의 분산계수 d가 각각 0.02와 0.01의 값을 가져 앙상블 spread-skill 관계가 거의 존재하지 않음을 보였다. 특히, 회귀계수에 제약을 두지 않은 HMR과 EMOS 방법에서 두 지점 모두 실제 관측된 기온보다 3~4oC 높게 예측하였지만 회귀계수가 음수가 되지 않도록 제약을 둔 HMR+와 EMOS+ 방법의 예측치는 관측과 유사하게 나타났다.
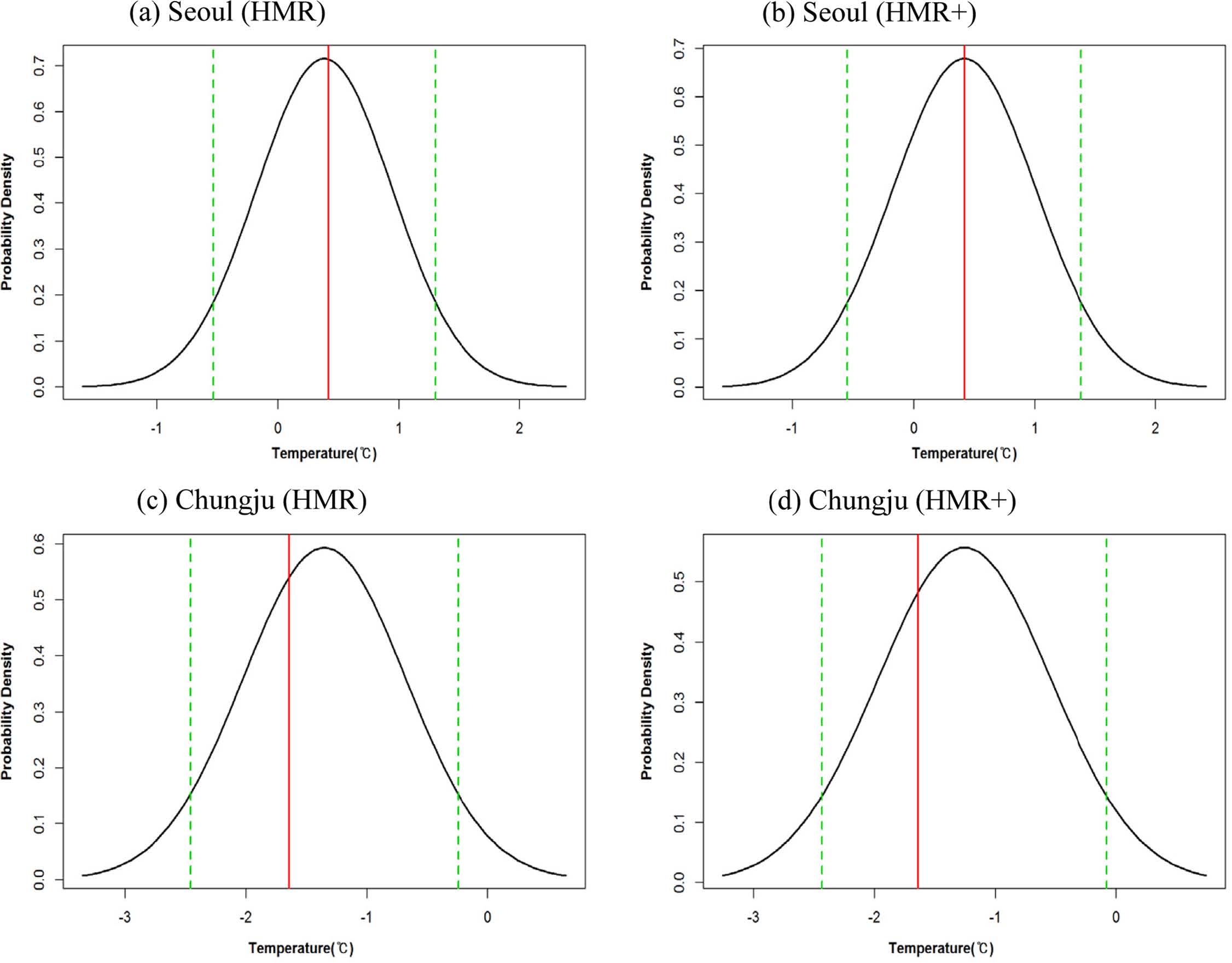
Predictive probability density function for one month of predicted temperature for the two selected stations of Seoul and Chungju (in January 2007). The 90% prediction interval (dotted lines) and the observation (full line) are shown.
Table 5는 천안과 강화지역의 다중선형회귀방법 별 검증기간에 대한 통계분석을 나타낸 것이다. Table 4에서 나타난 것과 같이 회귀계수에 제약을 두지 않은 HMR과 EMOS 방법에서 기온이 과대하게 추정되었다. 그 결과 편의가 약 0.3~0.4oC, 평균제곱근오차가 1oC 이상으로 비교적 크게 나타났다. 하지만 회귀계수가 음수가 되지 않도록 제약을 둔 HMR+와 EMOS+방법에서는 편의가 크게 감소 하였으며 특히, 천안 지점의 편의는 거의 0에 가까운 값을 보였다. 또한, 분산비는 약 0.02 감소하였고 절대평균오차와 평균제곱근오차 역시 크게 감소하여 향상된 기온의 예측 성능을 보였다.
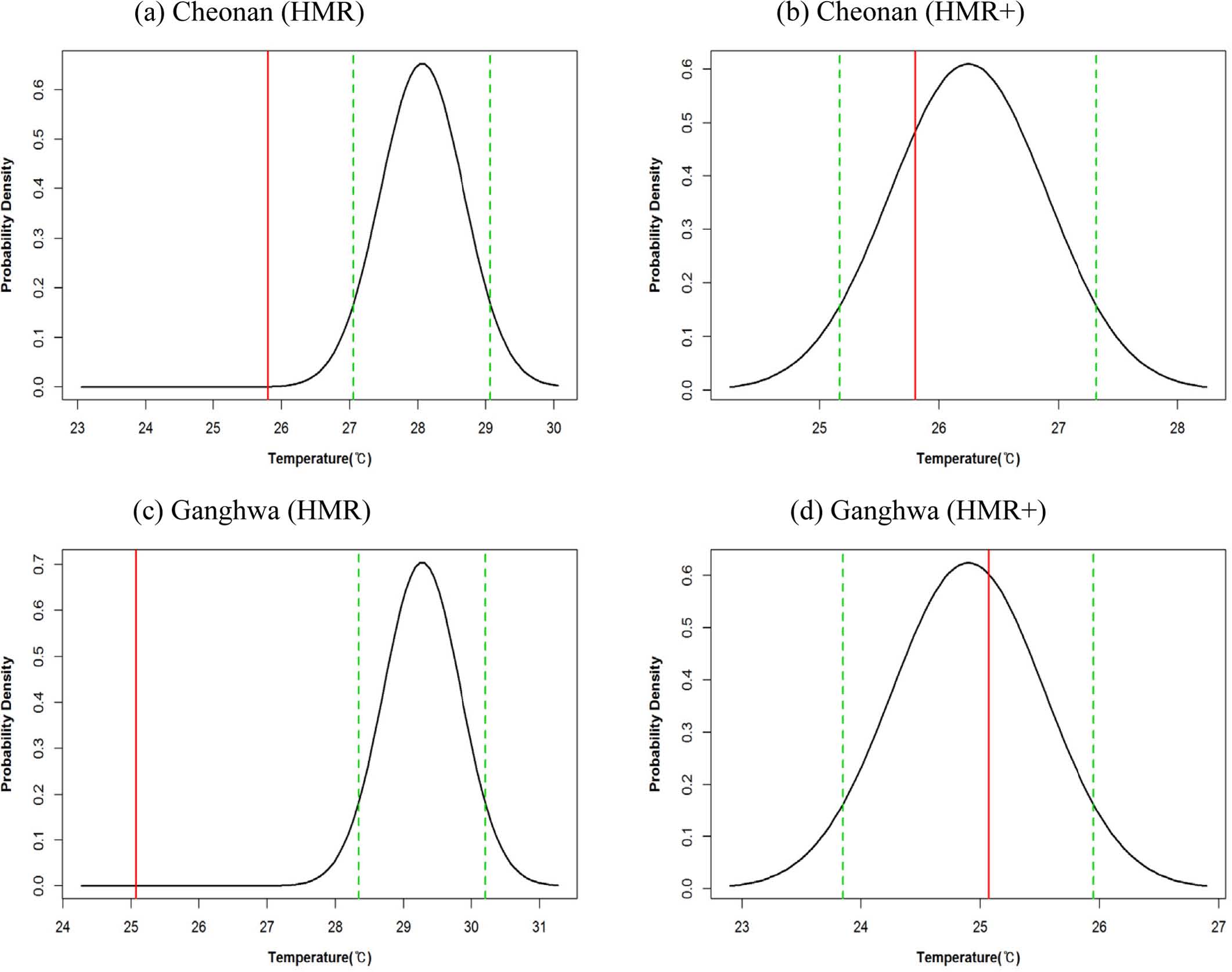
Figure 5는 천안과 강화 지점에서 HMR과 HMR+ 방법의 90% 예측구간을 나타낸 것이다. HMR 방법에서 두 지점의 관측값은 예측구간에서 상당히 벗어나 있음을 알 수 있다. Figure 5의 (a)와 (c)에서, 예측확률분포로부터 관측값이 발생될 확률은 거의 0이기 때문에 HMR 방법으로부터 산출된 기온은 실제 측정된 관측값에 비해 상당히 잘못 예측되었음을 알 수 있다. 하지만 회귀계수가 음수가 되지 않도록 제약을 둔 HMR+ 방법에서는 관측값이 예측확률밀도함수의 90% 예측구간 내에 위치하여 확률예측이 상당히 개선되었음을 보였다.
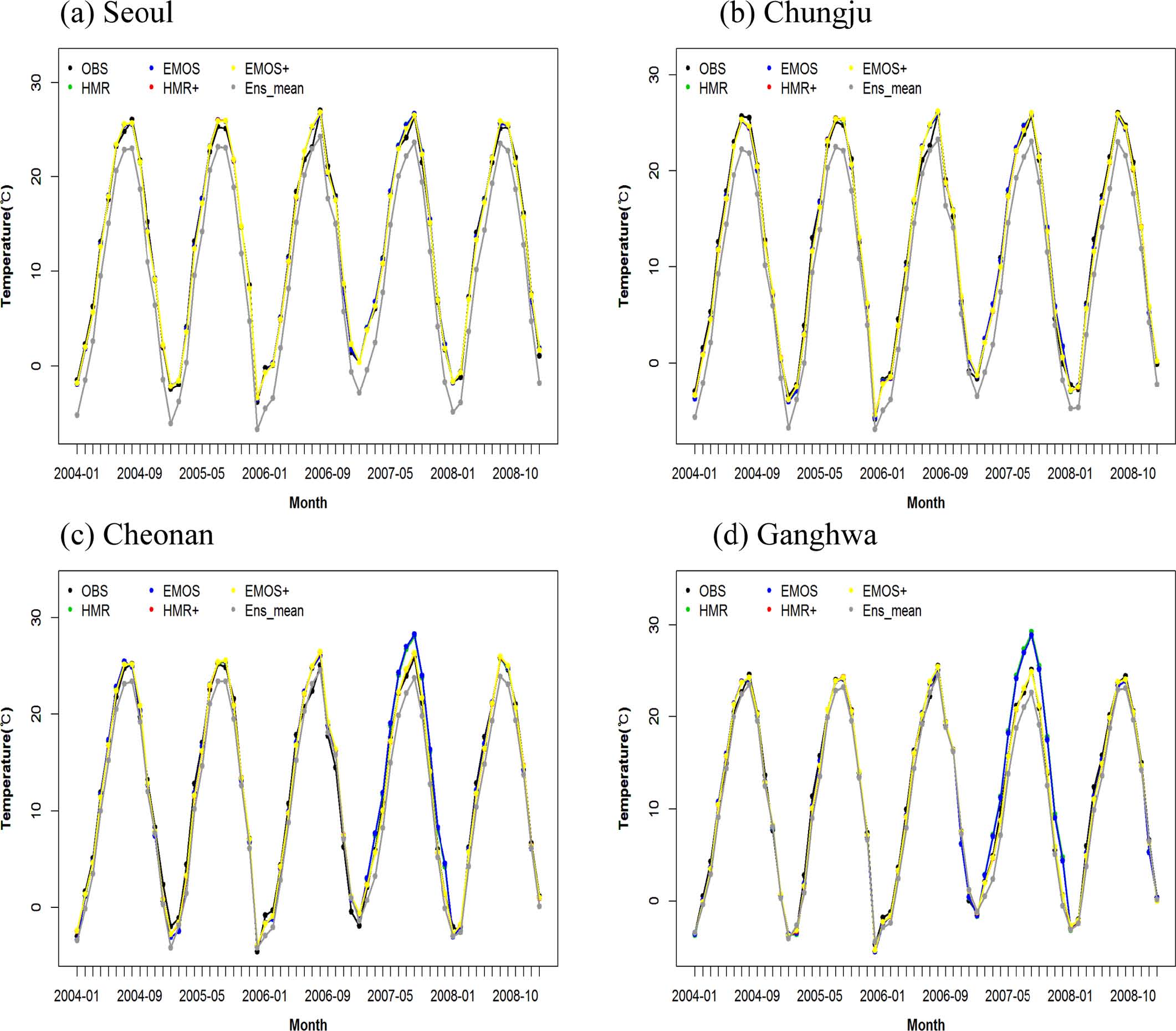
Time series of observation, simple ensemble mean, and four multiple linear regression methods for the selected 4 stations.
Figure 6은 검증기간에 대한 서울, 충주, 천안과 강화지점의 시계열을 나타낸 것이다. 검정색은 관측값, 녹색은 HMR, 파란색은 EMOS, 빨간색은 HMR+, 노란색은 EMOS+, 마지막으로 회색은 앙상블 평균을 나타낸다. 대부분의 지역에서 앙상블 평균 예측치는 관측값보다 기온을 과소추정하고 있는 것을 알 수 있다. 서울과 충주 지역에서 네 가지 다중선형회귀방법 모두 관측치와 비슷하게 기온을 잘 예측하여 다중회귀방법 별 차이는 거의 나타나지 않았다. 천안과 강화지역에서도 2007년을 제외한 기간에서는 네 가지 방법 모두 관측치와 유사하게 기온을 예측하는 것을 알 수 있다. 하지만 2007년에서 회귀계수에 제약을 두지 않은 HMR과 EMOS 방법은 관측보다 기온을 약 3~4oC 과대하게 예측하는 특징을 보였다.
천안과 강화 지역에서 HMR과 EMOS 방법이 관측보다 기온을 과대 예측하는 원인을 알아보기 위해 2007년의 각 앙상블 멤버와 관측값의 상자그림과 다중선형회귀방법 별 예측치에 대한 상자그림을 그려보았다(Fig. 7). 대부분의 앙상블 멤버들은 서로 비슷한 기온의 모의수준을 보였지만 SRCM_ERA, SRCM_R2와 WRF_R2가 관측보다 기온을 낮게 예측하였다. 특히, WRF_R2는 다른 앙상블 멤버들보다 평균 기온을 약 5oC 낮게, 기온의 변동성 또한 매우 작게 모의하였다. 따라서 훈련기간에서 존재하지 않던 이상치가 검증기간에서 나타나 다중선형회귀 결과에 영향을 준것으로 판단된다. 이러한 이상치들에 영향을 받아 다중선형회귀방법 별 기온의 예측값에 대한 상자그림에서 HMR과 EMOS 방법이 관측보다 기온을 과대하게 예측하는 것을 볼 수 있다. 반면 Table 4에 나타낸 것과 같이 회귀계수가 음수가 되지 않도록 제약을 둠으로써 WRF_R2의 가중치가 0이 되어 이상치가 제거되었기 때문에 HMR+와 EMOS+ 방법은 관측과 비슷한 기온값을 보였다.
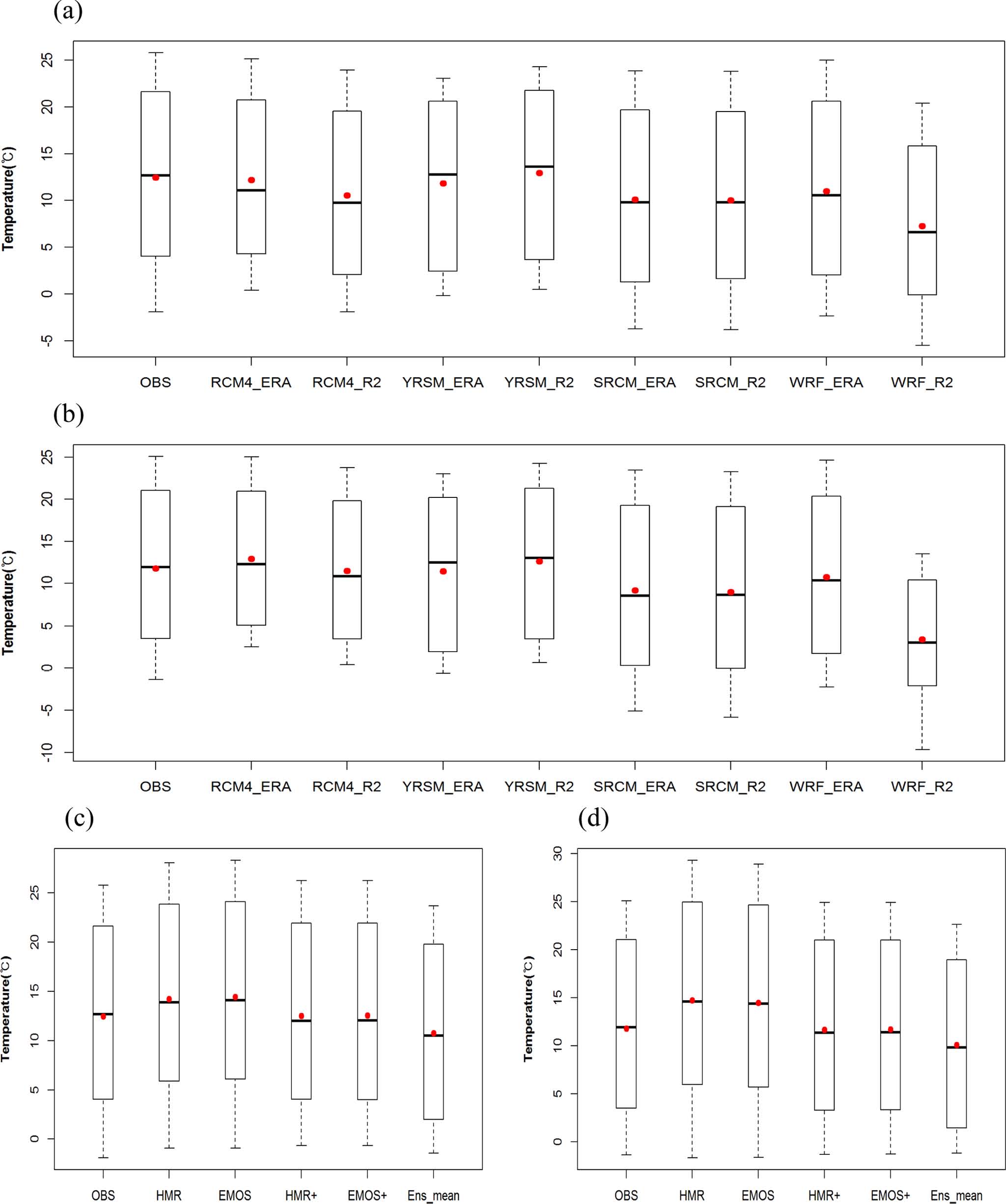
Box plot of observation and eight ensemble members in 2007 (top and middle). Bottom two figures show box plot of forecasts according to four multiple linear regression methods and ensemble mean in 2007. (a) and (c) indicate Cheonan and (b) and (d) indicate Gangwa.
Figure 8는 다중선형회귀방법 별 기온의 편의에 대한 공간분포를 나타낸 것이다. 여기서 삼각형은 강화지역, 별표는 서산 지역, 사각형은 천안 지역을 나타낸다. HMR과 EMOS 방법 간의 예측성능은 거의 차이가 없으며 HMR+와 EMOS+ 방법 역시 예측성능에 차이가 없는 것으로 나타났다. 검증기간에 이상치가 존재하는 강화, 서산과 천안 지역에서 회귀계수가 음수가 되지 않도록 제약을 둔 HMR+와 EMOS+ 방법에서 편의가 크게 감소하였다. 하지만 검증기간에 이상치가 존재하지 않는 나머지 지역에서는 네 방법 모두 비슷한 편의를 보였다.
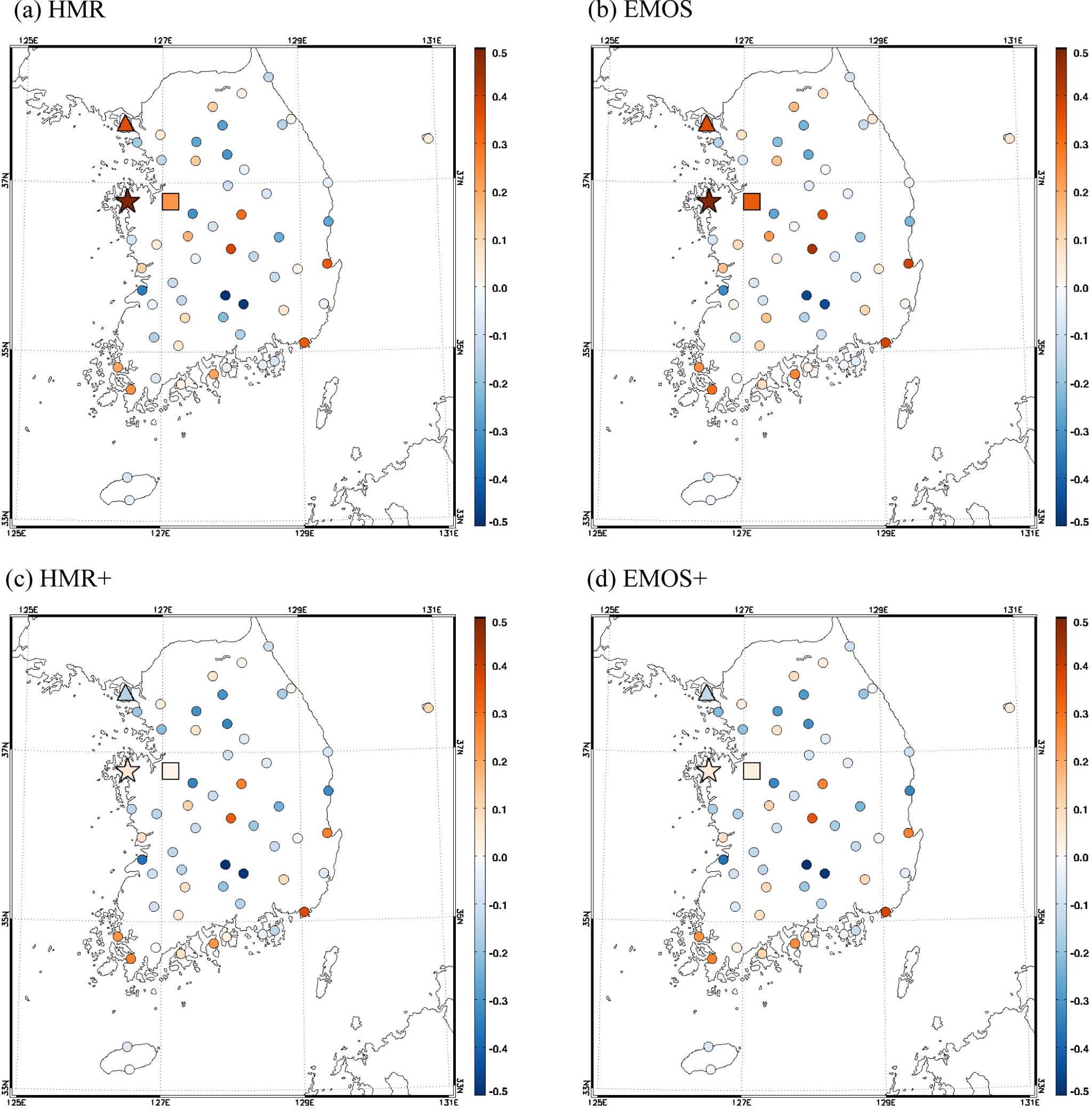
Spatial distribution of bias (oC) according to four multiple linear regression methods. The triangle, star, and square indicate Gangwa, Seosan, and Cheonan, respectively.
Table 6은 각 모델, 앙상블 단순 평균과 다중선형회귀방법 별 검증기간에서의 59개 관측 지점에 대한 평균 기온의 예측성능을 나타낸 것이다. YRSM_R2을 제외한 7개의 앙상블 멤버 모두 음의 편의를 보였다. 특히, SRCM_ERA와 SRCM_R2의 편의가 각각 −2.5oC, −2.6oC로 강한 음의 편의를 보였으며 절대평균오차와 평균제곱근오차가 다른 모델에 비해 큰 값을 가져 상대적으로 낮은 예측성능을 보였다. Figure 7에서 보는 것과 같이 다른 모델들에 비해 SRCM_ERA와 SRCM_R2 기온의 분포가 왼쪽으로 치우쳐져 있다. 이로부터 SRCM이 기온의 변동은 관측과 유사하게 모의하지만 평균적으로 기온을 과소하게 모의하고 있는 것을 알 수 있다. 그림으로 제시하지는 않았지만 대부분의 지점에서 이러한 특징이 나타났으며 이로 인해 SRCM의 예측 성능이 가장 낮았다. 하지만 분산비가 1에 가까운 값을 보여 기온의 변동성은 관측과 유사하였다. 또한, WRF_R2 역시 큰 음의 편의, 큰 절대평균오차와 평균제곱근오차를 보였다. 이 역시 Fig. 7에서 보는 것과 같이 일부 지역에서 WRF_R2가 2007년의 평균 기온과 변동을 낮게 모의하여 나타난 결과이다. 단순 앙상블 평균은 대부분의 모델보다 향상된 예측 성능을 보였으나 앙상블 멤버 중 예측 성능이 가장 뛰어난 RCM4_ERA보다는 낮은 예측 성능을 보였다. 다중선형회귀방법인 HMR과 EMOS 방법은 각 앙상블 멤버와 앙상블 평균보다 매우 향상된 예측 성능을 보였다. 특히, 회귀계수가 음수가 되지 않도록 제약을 둔 HMR+와 EMOS+ 방법은 이상치에 영향을 받지 않고 안정적으로 기온을 예측하여 가장 뛰어난 예측성능을 보였다. 대부분의 지점에서 EMOS와 EMOS+ 방법의 분산계수 d값이 거의 0에 가깝게 추정되었다. 따라서 HMR과 EMOS, HMR+와 EMOS+ 방법 간의 차이는 거의 나타나지 않았다.
5. 요약 및 결론
지역기후모델은 초기조건과 경계조건 등에 영향을 받기 때문에 그 결과에 불확실성이 내재되어 있다. 따라서 본 연구에서는 지역기후모델이 가지는 불확실성을 줄이기 위해 다중선형회귀방법인 HMR, EMOS, HMR+와 EMOS+를 사용하였다. 여기서 HMR 방법이란 일반적인 다중선형회귀방법이며, EMOS 방법은 Gneiting et al. (2005)이 제안한 방법으로, 앙상블 spread-skill 관계가 존재할 때, 잔차를 등분산이 아닌 앙상블 분산에 비례하도록 이분산으로 가정한 다중 선형회귀방법이다. 하지만 회귀계수의 추정치가 음수인 경우에는 가중치로써 해석이 어렵기 때문에 회귀계수가 음수가 되지 않도록 제약을 두었으며 이 방법을 HMR+와 EMOS+라고 하였다. 위 네 가지 다중선형회귀방법을 2개의 경계조건이 처방된 4개의 모델자료에 적용하여 다중선형회귀방법의 예측성능을 분석하였다. 각 모델의 모의 기간은 총 20년(1989~2008)이며 그 중 앞의 15년(1989~2003)을 훈련기간으로, 마지막 5년(2004~2008)을 검증기간으로 설정하였다. 다중선형회귀방법의 예측성능을 알아보기 위해 기상청 59개 관측지점 자료를 이용하였으며 그 중 서울, 충주, 천안과 강화 지역에 대한 결과를 제시하였다.
다중선형회귀방법을 적용하기에 앞서 지역기후모델들이 가지는 특징을 파악하기 위해 순위 히스토그램과 R-Q-Q 그래프를 사용하였다. 순위 히스토그램이 약한 U자형을 보이며 관측값의 순위가 오른쪽에 치우친 것으로 대부분의 모델들이 관측보다 기온과 기온의 변동성을 과소 모의하고 있음을 보였다.
검증기간에 이상치가 존재하지 않는 서울과 충주 지역에서 HMR과 EMOS 방법, HMR+와 EMOS+ 방법의 회귀계수에는 거의 차이가 없었다. 평균제곱근 오차를 기준으로 서울에서는 네 방법 모두 유사한 기온의 예측 성능을 보였고 충주에서는 EMOS+가 가장 뛰어난 기온의 예측 성능을 보였다. 또한 분산비는 거의 1에 가까운 값을 보여 네 방법 모두 기온의 변동성을 관측과 유사하게 예측하였다. 검증기간에 이상치가 존재하는 천안과 강화 지역 역시 HMR과 EMOS 방법, HMR+와 EMOS+ 방법 간의 차이는 거의 존재하지 않았다. 하지만 회귀계수가 음수가 되지 않도록 제약을 둔 HMR+와 EMOS+ 방법에서 WRF_R2의 가중치를 나타내는 β8의 회귀계수가 0이 되어 검증기간에 나타난 WRF_R2의 이상치를 제거하였다. 그 결과 천안에서 검증기간의 평균제곱근오차가 약 0.3~0.4oC, 강화에서 약 0.8~1.0oC 감소하여 안정적인 기온의 예측성능을 보였다. 또한 59개 모든 지점의 평균 통계 값에서 다중선형회귀를 이용한 방법이 각 앙상블 멤버와 앙상블 평균보다 좋은 예측 성능을 보였다. 회귀계수가 음수가 되지 않도록 제약을 둔 HMR+와EMOS+ 방법이 일부 지역의 검증기간에 존재하는 이상치에 영향을 받지 않고 안정적인 기온 예측을 하여 절대평균오차가 약 0.02oC, 평균제곱근오차가 약 0.05oC 감소하여 가장 좋은 기온의 예측성능을 보였다. 대부분의 지점에서 EMOS와 EMOS+ 방법의 분산계수 d값이 거의 0에 가깝게 추정되었다. 이는 등분산의 가정과 유사하기 때문에 HMR과 EMOS, HMR+와 EMOS+ 방법 간의 예측성능은 거의 차이가 없었다. 따라서 이상치의 영향을 받지 않고 비교적 계산이 간편한 HMR+ 방법을 사용하여 기온예측을 하는 것이 좋을 것으로 판단된다.
Acknowledgments
본 연구는 “기후변화 감시 · 예측 및 국가정책지원강화사업”의 일환으로 한국기상산업진흥원(KMIPA2015-2084)의 지원으로 수행되었습니다.
References
-
Chandler, R. E., (2005), On the use of generalized linear models for interpreting climate variability, Environmetrics, 16, p699-715.
[https://doi.org/10.1002/env.731]

-
Choi, S. J., D. K. Lee, and S. G. Oh, (2011), Regional climate simulations over East-Asia by using SNURCM and WRF forced by HadGEM2-AO, J. Korean Earth Sci. Soc, 32, p750-760.
[https://doi.org/10.5467/JKESS.2011.32.7.750]

-
Christensen, J. H., and O. B. Christensen, (2007), A summary of PRUDENCE model projections of changes in European climate by the end of this century, Clim. Change, 81, p7-30.
[https://doi.org/10.1007/s10584-006-9210-7]

-
Christensen, J. H., E. Kjellström, F. Giorgi, G. Lenderink, and M. Rummukainen, (2010), Weighting assignment in regional climate models, Climate Res, 44, p179-194.
[https://doi.org/10.3354/cr00916]

-
Chu, P. S., and X. Zhao, (2004), Bayesian change-point analysis of tropical cyclone activity: The Central North Pacific case, J. Climate, 17, p4893-4901.
[https://doi.org/10.1175/JCLI-3248.1]

-
Cui, B., Z. Toth, Y. Zhu, and D. Hou, (2012), Bias correction for global ensemble forecast, Wea. Forecasting, 27, p396-410.
[https://doi.org/10.1175/WAF-D-11-00011.1]

-
Dai, Y. H., (2002), Convergence properties of the BFGS algorithm. SIAM, J. Optim, 13, p693-701.
[https://doi.org/10.1137/S1052623401383455]

-
Feng, J., D. K. Lee, C. Fu, J. Tang, Y. Sato, H. Kato, J. Megregor, and K. Mabuchi, (2011), Comparison of four ensemble methods combining regional climate simulations over Asia, Meteor. Atmos. Phys, 111, p41-53.
[https://doi.org/10.1007/s00703-010-0115-7]

-
Fu, C., S. Wang, Z. Xiong, W. J. Gutowski, D. K. Lee, J. L. McGregor, Y. Sato, H. Kato, J. W. Kim, and M. S. Suh, (2005), Regional climate model intercomparison project for Asia, Bull. Amer. Meteor. Soc, 86, p257-266.
[https://doi.org/10.1175/BAMS-86-2-257]

-
Gates, W. L., (1992), AMIP: The Atmospheric Model Intercomparison Project, Bull. Amer. Meteor. Soc, 73, p1962-1970.
[https://doi.org/10.1175/1520-0477(1992)073<1962:ATAMIP>2.0.CO;2]

-
Gemmer, M., T. Fischer, T. Jiang, B. Su, and L. L. Liu, (2011), Trends in precipitation extremes in the Zhujiang river basin, South China, J. Climate, 24, p750-761.
[https://doi.org/10.1175/2010JCLI3717.1]

-
Giorgi, F., M. R. Marinucci, and G. T. Bates, (1993a), Development of a second generation regional climate model (RegCM2). Part I: boundary layer and radiative transfer processes, Mon. Wea. Rev, 121, p2794-2813.
[https://doi.org/10.1175/1520-0493(1993)121<2794:DOASGR>2.0.CO;2]

-
Giorgi, F., M. R. Marinucci, G. T. Bates, and G. DeCanio, (1993b), Development of a second generation regional climate model (RegCM2). Part II: convective processes and assimilation of lateral boundary conditions, Mon. Wea. Rev, 121, p2814-2832.
[https://doi.org/10.1175/1520-0493(1993)121<2814:DOASGR>2.0.CO;2]

- Giorgi, F., and Coauthors , (2001), Regional climate change information-Evaluation and projections, In J. Climate change 2001: The Scientific Basis, Houghton, J. T. Eds, et al , Cambridge University Press, p583-638.
- Giorgi, F., C. Jones, and G. R. Asrar, (2009), Addressing climate information needs at the regional level: The CORDEX framework, WMO Bull, 58, p175-183.
-
Giorgi, F., and Coauthors , (2012), RegCM4: model description and preliminary tests over multiple CORDEX domains, Climate Res, 52, p7-29.
[https://doi.org/10.3354/cr01018]

-
Gneiting, T., A. E. Raftery, A. H. Westveld III, and Goldman, T., (2005), Calibrated probabilistic forecasting using ensemble model output statistics and minimum CRPS estimation, Mon. Wea. Rev, 133, p1098-1118.
[https://doi.org/10.1175/MWR2904.1]

- Grell, G., J. Dudhia, and D. Stauffer, (1994), A description of the fifthgeneration Penn State/NCAR Mesoscale Model (MM5), NCAR Tech, Note NCAR/TN-398 1 STR, p121.
-
Hamill, T. M., (2001), Interpretation of rank histograms for verifying ensemble forecasts, Mon. Wea. Rev, 129, p550-560.
[https://doi.org/10.1175/1520-0493(2001)129<0550:IORHFV>2.0.CO;2]

-
Hersbach, H., (2000), Decomposition of the continuous ranked probability score for ensemble prediction systems, Wea.Forecasting, 15, p559-570.
[https://doi.org/10.1175/1520-0434(2000)015<0559:DOTCRP>2.0.CO;2]

-
Hong, S. Y., and Coauthors , (2013), The global/regional integrated model system (GRIMs), Asia-Pacific J. Atmos. Sci, 49, p219-243.
[https://doi.org/10.1007/s13143-013-0023-0]

- IPCC, (2014), Climate Change 2014: Impacts, Adaption, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, V. R. Barros Eds, et al , Cambridge University Press, p688.
-
Juang, H. M., H, S. Y. Hong, and M. Kanamitsu, (1997), The NCEP regional spectral model: An update, Bull. Amer. Meteor. Soc, 78, p2125-2143.
[https://doi.org/10.1175/1520-0477(1997)078<2125:TNRSMA>2.0.CO;2]

- Kalnay, E., (2003), Atmospheric Modeling, Data Assimilation and Predictability, Cambridge University Press, p341.
-
Kanamitsu, M., A. Kumar, H. M. H. Juang, J. K. Schemm, W. Wang, F. Yang, S. Y. Hong, P. Peng, W. Chen, S. Moorthi, and M. Ji, (2002), NCEP dynamical seasonal forecast system 2000, Bull. Amer. Meteor. Soc, 83, p1019-1037.
[https://doi.org/10.1175/1520-0477(2002)083<1019:NDSFS>2.3.CO;2]

-
Kim, C., and M. S. Suh, (2013), Prospects of using Bayesian model averaging for the calibration of one-month forecasts of surface air temperature over South Korea, Asia-Pacific J. Atmos. Sci, 49, p301-311.
[https://doi.org/10.1007/s13143-013-0029-7]

-
Krishnamurti, T. N., C. M. Kishtawal, T. E. LaRow, D. R. Bachiochi, Z. Zhan, C. E. Williford, S. Gadgil, and S. Surendran, (1999), Improved weather and seasonal climate forecasts from a multimodel superensemble, Science, 285, p1548-1550.
[https://doi.org/10.1126/science.285.5433.1548]

-
Lee, J. W., S. Y. Hong, E. C. Chang, M. S. Suh, and Suh Kang, (2014), Assessment of future climate change over East Asia due to RCP scenarios downscaled by GRIMs-RMP, Climate Dyn, 42, p733-747.
[https://doi.org/10.1007/s00382-013-1841-6]

-
Marzban, C., R. Wang, F. Kong, and S. Leyton, (2011), On the effect of correlations on rank histograms: reliability of temperature and wind speed forecasts from finescale ensemble reforecasts, Mon. Wea. Rev, 139, p295-310.
[https://doi.org/10.1175/2010mwr3129.1]

- Mearns, L. O., M. Hulme, T. R. Carter, R. Leemans, M. Lal, P. Whetton, L. Hay, R. N. Jones, R. Katz, T. Kittel, J. Smith, and R. Wilby, (2001), Climate scenario development, In Climate Change 2001: The Scientific Basis, J. T. Houghton Eds., and , Cambridge University Press, p741-770.
-
Meehl, G. A., F. Zwiers, J. Evans, T. Knutson, L. Mearns, and P. Whetton, (2000a), Trends in extreme weather and climate events: Issues Related to Modeling Extremes in Projections of Future Climate Change, Bull. Amer. Meteor. Soc, 81, p427-436.
[https://doi.org/10.1175/1520-0477(2000)081<0427:TIEWAC>2.3.CO;2]

-
Meehl, G. A., G. J. Boer, C. Covey, M. Latif, and R. J. Stouffer, (2000b), The Coupled Model Intercomparison Project (CMIP), Bull. Amer. Meteor. Soc, 81, p313-318.
[https://doi.org/10.1175/1520-0477(2000)081<0313:TCMIPC>2.3.CO;2]

- Myoung, J. S., S. G. Oh, and M. S. Suh, (2012), Improvement of simulated air temperature of regional climate model using linear regression method, Korean J. Climate Research, 7, p255-270.
-
Peng, P., A. Kumar, and H. van den Dool, (2002), An analysis of multimodel ensemble prediction for seasonal climate anomalies, J. Geophys. Res, 107.
[https://doi.org/10.1029/2002JD002712]

-
Raftery, A. E., T. Gneiting, F. Balabdaoui, and M. Polakowski, (2005), Using Bayesian model averaging to calibrate forecast ensembles, Mon. Wea. Rev, 133, p1155-1174.
[https://doi.org/10.1175/MWR2906.1]

- Skamarock, W. C., and Coauthors , (2008), A description of the advanced research WRF version 3, NCAR Tech, Note NCAR/TN-475+STR, p113.
-
Suh, M. S., and D. K. Lee, (2004), Impacts of land use/cover changes on surface climate over east Asia for extreme climate cases using RegCM2, J. Geophys. Res, 109.
[https://doi.org/10.1029/2003JD003681]

-
Suh, M. S., S. G. Oh, D. K. Lee, D. H. Cha, S. J. Choi, C. S. Jin, and S. Y. Hong, (2012), Development of new ensemble methods based on the performance skills of regional climate models over South Korea, J. Climate, 25, p7067-7082.
[https://doi.org/10.1175/JCLI-D-11-00457.1]

- van der Linden, P., and J. F. B. Mitchell, (2009), ENSEMBLES:Climate change and its impacts at seasonal, decadal and centennial timescales, Summary of research and results from the ENSEMBLES project, Met Office Hadley Centre, p160.
-
Wilks, D. S., (2002), Smoothing forecast ensembles with fitted probability distributions, Quart. J. Roy. Meteor. Soc, 128, p2821-2836.
[https://doi.org/10.1256/qj.01.215]

- Wilks, D. S., (2006), Statistical methods in the atmospheric science, 2nd ed, International Geophysics Series, 59, Academic Press, p627.
-
Yun, K. S., K. Y. Heo, J. E. Chu, K. J. Ha, E. J. Lee, Y. Choi, and A. Kitoh, (2012), Change in climate classification and extreme climate indices from a high-resolution future projection in Korea, Asia-Pac. J. Atmos. Sci, 48, p213-226.
[https://doi.org/10.1007/s13143-012-0022-6]

-
Yun, W. T., L. Stefanova, and T. N. Krishnamurti, (2003), Improvement of the multimodel superensemble technique for seasonal forecasts, J. Climate, 16, p3834-3840.
[https://doi.org/10.1175/1520-0442(2003)016<3834:IOTMST>2.0.CO;2]