고밀도 지상강우관측망을 활용한 서울지역 정량적 실황강우장 산정
Abstract
For urban flash flood simulation, we need the higher resolution radar rainfall than radar rainfall of KMA, which has 10 min time and 1km spatial resolution, because the area of subbasins is almost below 1 km2. Moreover, we have to secure the high quantitative accuracy for considering the urban hydrological model that is sensitive to rainfall input. In this study, we developed the quantitative precipitation estimation (QPE), which has 250 m spatial resolution and high accuracy using KMA AWS and SK Planet stations with Mt. Gwangdeok radar data in Seoul area. As the results, the rainfall field using KMA AWS (QPE1) is showed high smoothing effect and the rainfall field using Mt. Gwangdeok radar is lower estimated than other rainfall fields. The rainfall field using KMA AWS and SK Planet (QPE2) and conditional merged rainfall field (QPE4) has high quantitative accuracy. In addition, they have small smoothed area and well displayed the spatial variation of rainfall distribution. In particular, the quantitative accuracy of QPE4 is slightly less than QPE2, but it has been simulated well the non-homogeneity of the spatial distribution of rainfall.
Keywords:
High density, rain gauge network, quantitative precipitation estimation, Seoul, conditional merging1. 서 론
최근 전 세계적인 기후변화 및 기상이변으로 인해 국지적 집중호우의 발생 빈도가 증가하고 있으며, 홍수발생으로 인명과 재산피해가 증가하고 있는 실정이다. 우리나라도 예외는 아니며, 특히 도시지역의 경우 급속한 도시화 및 개발에 따라 유입시간(inlet time)의 단축, 도달시간(concentration time)의 감소, 첨두유량(peak flow)의 증가, 통수능(conveyance) 증가, 저류량(detention storage) 감소 등 전반적인 수문현상의 변화로 그 피해가 가중되고 있다.
일반적으로 도시수문 시스템의 설계 및 해석을 위해 필요한 강우자료 분해능은 시간분해능 1분~수분, 공간분해능 1 km2, 강우강도 추정의 불확실성은 10~50 mm h-1 범위에서 10% 미만이어야 한다(Schilling, 1991). 특히, 도시돌발홍수 모의를 위해 사용하는 도시유출모형은 하나의 배수체계(drainage network)를 하수관망과 맨홀, 토지이용과 같은 지형정보를 기준으로 세분화한다. 이를 소배수분구라고 하며, 일반적으로 그 면적은 대부분 1 km2 이하이기 때문에 기존 기상청에서 제공하는 레이더 강우정보(공간분해능 1~2 km)보다 해상도가 높은 실황강우정보가 필요하다. 또한, 강우량에 민감한 도시유출해석 모형의 특성을 고려하여 보다 정량적인 강우강도 정확도가 확보되어야 한다.
현재까지 국내에서는 레이더 강우의 정확도 개선을 위해 다양한 연구를 수행한 바 있다. Eom et al. (1996)은 레이더를 이용한 유역강우 산정기법 연구를 통해 레이더 반사강도의 정량적 분석과 함께 실측강우량과 레이더 강우량의 관측소별 보정계수를 산출하여 유역에 대한 강우량 산출을 연구하였다. 또한 Marshall and Palmer (1948)의 Z-R 관계식을 활용한 레이더 추정강우가 통상적으로 지상관측강우에 비해 과소추정되는 단점을 보완하기 위하여 Kim et al. (2002)은 WPMM (Window Probability Matching Method) 방법을 이용한 Z-R 관계식을 산출하여 기존의 Z-R 관계식과 비교 · 검토하였으며, 정량적인 강우량 산출 여부를 검증하였다. Bae et al. (2005)은 편차보정 기법을 적용하여 레이더 강우를 개선하고 불확실성이 유출 모형에 미치는 영향을 평가하였으며, Kim et al. (2007)은 조건부 합성 기법을 이용하여 레이더 강우를 보정하고 분포형 유출 모형인 VfloTM에 적용하였다. Yoon and Bae (2013)은 지형성 강우의 영향을 고려하여 레이더 최적강우장을 산정하는 기법을 개발하여 레이더 강우장의 정확도를 개선하고, 개선 결과를 도시홍수 예보모형에 적용하여 그 활용성을 평가한 바 있다. 현재까지의 연구는 지상강우 관측정보를 정량적인 참값으로 보고 레이더 강우장을 개선하는 것이 기본적이다. 그러나 지상강우에 의한 보정은 레이더와 우량계들이 서로 다른 자연적인 오차를 포함한 관측치를 제공하므로, 보정시 오차가 포함될 수밖에 없다. 예를 들어 일반적으로 사용되는 전도식(tipping bucket) 우량계는 상대적으로 정확한 장비이지만 전도형 버켓의 메커니즘에 의해 관측 체적(volumetric) 오차의 영향을 받는다. 또한, 경제적, 환경적 이유로 고밀도 관측망의 구축 및 유지가 어려웠다. 따라서 몇 지점의 우량계들만으로 유역을 대표하는 강우를 관측하여 전체적인 레이더 강우량의 정확도를 향상시키는 것 또한 여러 문제를 유발시켰다.
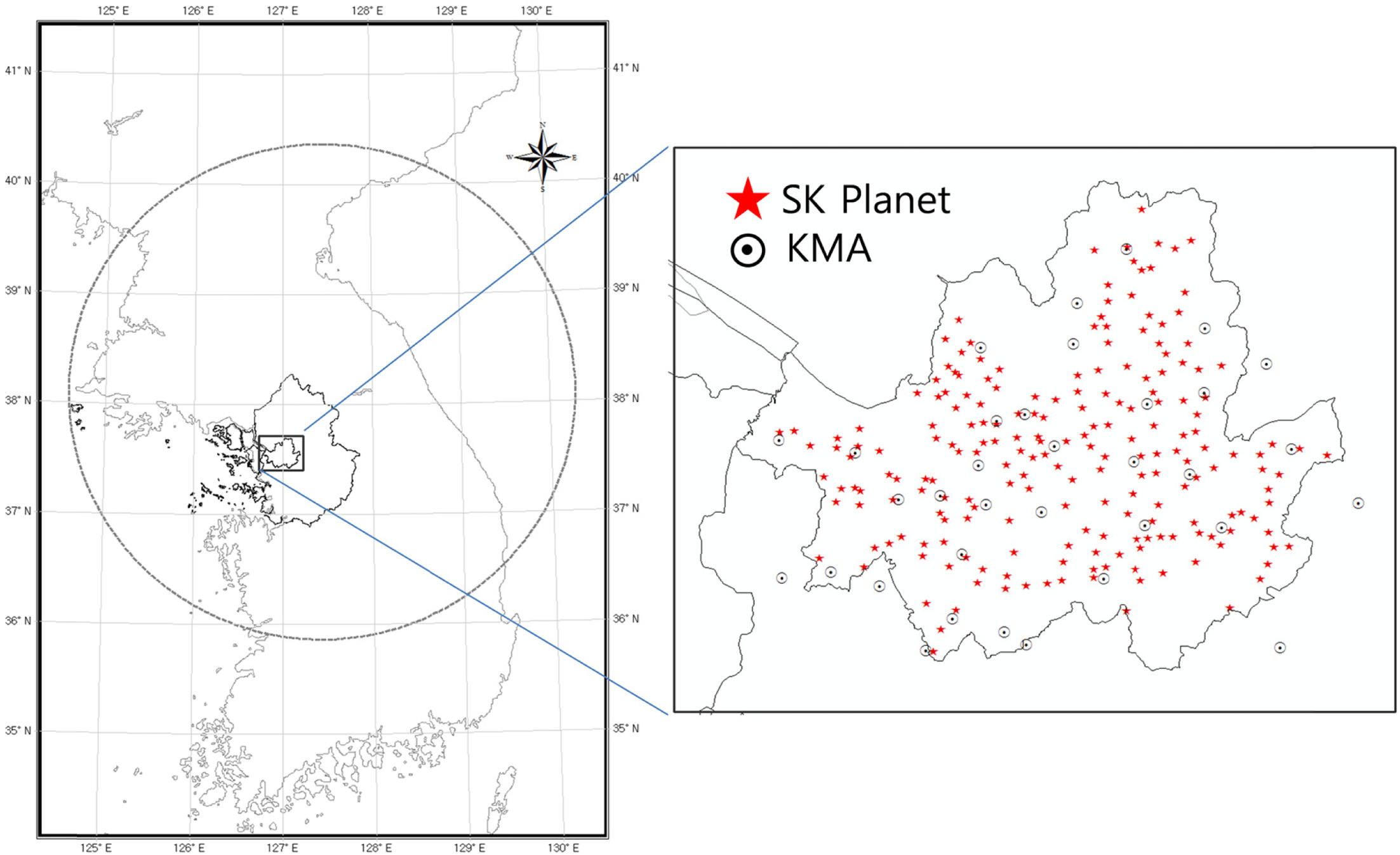
현재 서울지역의 강우관측을 위해 설치되어 있는 관측소는 기상청 35개소, 서울특별시 47개소, 국토해양부 5개소 등이 있다. 이들 관측장비는 각 기관별 운영목적에 따라 관측장비, 관측요소, 관측간격 등이 다르므로 이를 융합하여 활용하는 것에는 한계가 있었다. 특히, 도시지역에서 빈번하게 발생하는 국지적인 집중호우나 돌발적인 기상 현상 등은 강우지속시간이 짧기 때문에 10분~1시간 단위 관측을 하는 서울특별시나 국토해양부의 관측망으로는 강우관측에 한계가 존재한다. 또한, 발생 범위도 협소하기 때문에 현재의 관측망으로는 강우가 탐지되지 않는 경우가 빈번하다. 다만, 2013년부터 SK 텔레콤의 자회사인 SK 플래닛에서는 SK 텔레콤의 기지국 인프라를 활용해 복합기상 센서망을 구축하고 있으므로 기존 관측망과 함께 융합하여 사용하게 되면, 서울지역을 대상으로 하는 고밀도 관측망을 구축할 수 있다. 이에 본 연구에서는 기존 기상청, SK 플래닛에서 서울지역에 설치하여 운영 중인 고밀도 지상강우관측망과 광덕산 레이더 원자료를 이용하여 정량적 정확도를 확보한 250 m해상도의 실황강우장을 산정하는 것을 최종 목적으로 한다. 또한 강우산정의 불확실성을 고려하여 지상관측강우나 레이더 자체 정보만을 이용한 실황 강우장을 산정하여 관측망 밀도 및 레이더 자료 활용에 따른 정확도 및 유용성을 함께 평가하고자 한다.
2. 대상지역 및 사용자료
본 연구에서는 광덕산 레이더 관측자료를 이용하여 레이더 강우를 추정하고, 서울시 190개 강우관측망(기상청 34개소, SK 플래닛 156개소)의 관측자료를 실황강우장 산정에 이용하였다.
광덕산 레이더 사이트(Gwangdeoksan, GDK)는 서울에서 북동쪽으로 100 km 떨어져 있는 광덕산(1,046 m) 정상부근에 위치하고 있는데, 경기 및 강원북부지방의 집중호우 등 악기상 감시를 위해 2003년 12월 10일부터 관측 및 분석 업무를 수행하기 시작하였다. 광덕산 레이더는 파장 10 cm, 빔폭 1.0o인 S밴드 레이더로써 운영전략으로는 게이트 사이즈 250 m, 전체 관측반경은 480 km, 최적반경은 240 km, 0.0~20o까지 총 12개의 고도각 관측을 수행하고 있다. 본 연구에서 사용된 광덕산 레이더의 반사도 자료는 기상청에서 운용하는 레이더 품질관리 절차에 따라 품질 처리된 10분 간격의 UF 이진(binary)자료이다. 본 연구에서는 광덕산 레이더 강우는 1.5 km 고도의 CAPPI (Constant altitude plan position indicator) 반사도를 Marshall-Palmer 관계식(Z = 200R1.6)을 이용하여 추정하였다(Mohr and Vaughan, 1979).
지상강우관측자료는 기상청 Automatic Weather Station (AWS)와 SK 플래닛의 고밀도 관측망을 통해 관측된 자료를 활용하였다. SK 플래닛의 고밀도 관측망은 다음 Fig. 1의 빨간색 별과 같이 서울시 내에 총 262개의 기상 관측센서를 설치하여 운영하고 있으며, 2014년에는 경기도 및 6대 광역시에 1,800여 개를 설치하고, 2015년에는 약 4,000개소의 전국망을 구축 계획을 가지고 있다. Figure 1의 검은색 원은 기상청에서 운영 중인 관측소이다. SK 플래닛이 설치한 복합 기상센서는 기상청 표준을 준수한 장비이며, Table 1과 같이 기상청 AWS와 유사한 기상관측요소를 매 1분단위로 관측하여 실시간 수집하고 있다. 또한, SK 플래닛에서는 정기적인 기지국 유지 · 보수 인력을 활용한 자동화, 반자동 관측정보 품질관리 시스템을 이용하여 관측자료를 관리하고 있으며, 인근 기상청 AWS와의 비교를 통해 관측의 신뢰도가 확인되었다(www.weatherplanet.co.kr; Yoon et al., 2015).
지상우량계 자료는 Yoon et al. (2015)이 제시한 결측 및 이상치 보정절차를 따라 품질검정이 완료된 총 190개소 자료를 활용하였다. 지상우량계의 관측간격은 1분 단위이나 레이더와의 결합을 고려하여 본 연구에서는 10분 누적강우로 변환하여 사용하였으며, 서울시 전역에 총 190개소의 관측소를 사용하므로 평균 공간해상도는 약 3 km2이다. 본 연구에서 사용한 호우사례는 2013년 7월 12~15일과 7월 22일의 집중호우 사례로 모두 장마전선으로 인해 서울을 포함한 수도권 지역에 강우가 발생하였다.
3. 방 법
본 연구에서는 서울지역의 정량적 실황강우장을 강우관측자료와 강우산정방법에 따른 불확실성을 고려하여 총 4 종류로 구분하여 산정하였다. 산정한 실황 강우장은 기상청의 강우관측망 정보만을 이용하여 크리깅(Kriging)으로 산정된 실황강우장(QPE1), 기상청 강우관측망에 SK 플래닛 관측망을 결합하여 크리깅으로 산정된 실황강우장(QPE2), Marshall-Palmer 관계식으로 추정된 광덕산레이더 강우(QPE3), 조건부합성으로 통해 산정된 최적레이더 실황강우장(QPE4)이다.
3.1 정규크리깅(ordinary kriging)
지상관측강우를 이용하여 강우를 공간분포시키고, 조건부합성기법의 입력자료를 만들기 위해 정규크리깅 기법을 이용하였다. 크리깅은 부분적으로 획득된 정보를 바탕으로 최소자승 회귀분석 방법에 기반하여 내삽을 통해 미지점의 값을 예측하는 방법이다. 크리깅을 이용하여 예측하고자 하는 지점의 값을 구하기 위해서는 기지점의 가중치를 결정하여야 한다. 가중치를 구하는 방법 중 크리깅 추정식이 편향(bias)되지 않으면서 오차분산을 최소로 하는 크리깅을 정규크리깅이라 한다. 미지의 위치 0에서의 정규크리깅 추정치는 Eq. (1)과 같이 표현된다.
| (1) |
여기서, z0*는 위치가 알려진 지점에서 크리깅을 이용한 예측치, zi는 이미 그 위치와 값을 알고 있는 주위의 자료 값, λi는 각 자료의 가중치, 그리고 n은 크리깅 예측을 위해 사용한 자료의 총 개수이다. Equation (1)의 정규크리깅 가중치 λi는 오차분산을 최소로 하는 조건 Eq. (2)와 Eq. (1)의 크리깅 식이 편향되지 않을 조건 Eq. (3)을 만족하도록 결정되어져야 한다.
| (2) |
| (3) |
크리깅 식에 사용된 모든 자료는 실제 주어진 자료이므로 동일한 평균값을 가지게 된다. 따라서 Eq. (1)의 크리깅 추정식이 항상 편향되지 않기 위해서는 가중치의 합이 1이 되어야 한다. 이러한 제약조건하에서 Eq. (2)로 주어진 오차분산을 최소로 하는 가중치를 구하고 이들 가중치를 이용하여 알려진 값들의 선형결합으로 미지값이 예측된다(Goovaerts, 1997; Yoon, 2011).
3.2 조건부 합성기법
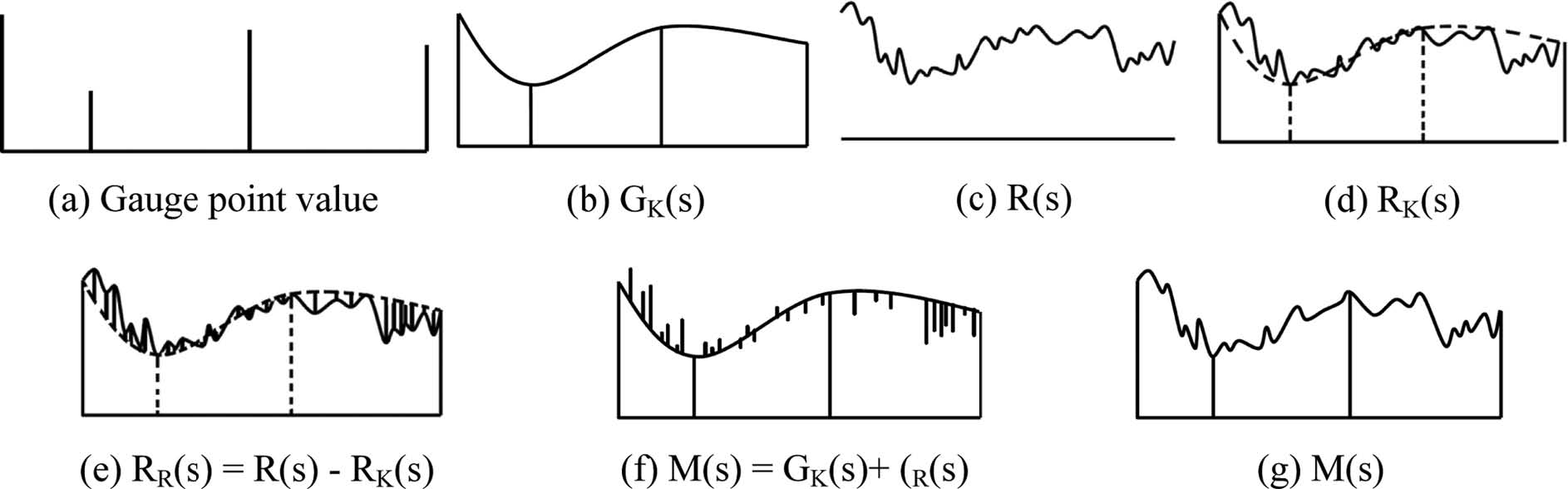
조건부 합성기법은 강우의 공간적 분포를 좀 더 정확하게 구현하면서 정량적 정확도를 확보할 수 있도록 지상강우관측망뿐만 아니라 레이더 정보를 함께 사용하여 QPE4를 산정하는 데 활용되었다. 조건부 합성기법은 Ehret (2002)과 Pegram (2002)에 의해 처음 제안되었으며, 강우장의 공간적 구조는 레이더 자료로부터 얻어지는 반면에 강우량은 지점 강우를 합성함으로써 얻어진다. 이 기법의 가정은 레이더는 정확한 강우량 보다는 정확한 공간적인 상대강우, 즉, 공간적 구조를 갖는다는 점에서 시작된다(Sinclair and Pegram, 2005). Figure 2는 조건부 합성기법의 개념을 나타낸 것이다(Sinclair and Pegram, 2005).
Figure 2의 기본 개념을 보다 자세히 설명하면 다음과 같다.
(a) 강우관측소 지점에서 점강우량 관측을 나타낸다.
(b) 관측된 점강우량을 크리깅 기법을 사용하여 공간분포 시킨다.
(c) 레이더에서 관측된 공간강우량을 나타낸다.
(d) 레이더 관측값 중 지상관측소와 같은 위치에 있는 값들을 이용하여, 크리깅 기법을 사용하여 공간분포 시킨다.
(e) 크리깅 기법의 경우 점 자료를 이용하여 미지의 공간 값을 산정하는 내삽기법이기 때문에 실제 레이더에 의해 추정된 공간분포 결과인 Fig. 2c와 크리깅기법을 사용하여 산정한 공간분포인 Fig. 2d의 값은 차이가 난다. 따라서 Fig. 2e와 같이 Figs. 2c와 d 사이의 편차를 구한다.
(f) (e)에서 계산한 편차를 (b)에 적용하여 제거하면 지점의 값을 유지하면서 공간분포의 오차를 상쇄시킨 합성 강우장 Fig. 2g가 생성된다.
다음 Eqs. (4)~(9)은 조건부 합성 방법에 의해 보정되는 레이더 강우자료의 오차 구조를 수식으로 표현한 것이다.
| (4) |

Statistics of the comparison between the cross validation estimates of each quantitative precipitation estimations and rain gauge observations.
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
여기서, Z(s)는 격자 위치 s에서의 참강우장, GK(s)는 Z(s)를 구현하기 위해 우량계 지점 자료로부터 크리깅된 강우장, R(s)는 레이더 추정강우, RK(s)는 R(s)를 구현하기 위해 크리깅된 레이더 강우장이며, M(s)는 조건부 합성기법으로 보정된 레이더 강우 분포이다. εG(s) 는 s 지점의 참강우에 의해 기인하는 오차이며, 실제 참강우량을 정확히 할 수 없기 때문에 결정할 수 없는 값이다. εR(s)는 R(s)가 레이더 반사도로부터 변환된 레이더 강우자료이고, RK(s)가 R(s)로부터 크리깅된 값이기 때문에 알 수 있는 오차이다. Equation (6)은 조건부 합성된 강우장을 산정하는 데 이용된다. ρ는 εG(s)와 εR(s)의 상관계수이며, β는 εG(s)와 εR(s)의 분산의 합이다. Equations (7)~(9)는 참강우값과 합성된 강우값 사이의 오차분산을 기대값으로 정의한 것이다. 모든 강우장들을 가우시안분포라고 가정하면 오차의 기대값은 0이 되는데 조건부 합성에서 고려한 크리깅된 계산결과는 불편향(unbiased)된 값들이기 때문에 이러한 식들로 표현될 수 있다. 우량계 지점정보가 있는 지점에서의 오차분산은 0이 되는 반면, 분포장의 다른 지점에서는 오차가 존재한다. 이러한 오차는 εG(s)와 εR(s) 사이의 상관관계 ρ가 양의 값을 갖는 경우 β가 최대값으로 제한된다. 만약 εG(s)와 εR(s)이 1과 같이 강한 양의 상관관계를 갖는 경우, 우량계와 레이더 사이의 기대를 이용하여 Z(s)를 산정할 수 있다고 기대할 수 있다. 그러면 제안된 Eq. (9)와 같이 오차분산은 β보다 훨씬 작게 된다. 조건부 합성기법은 크리깅의 불편향 가정을 기본으로 참강우값의 오차를 레이더와 크리깅 강우장의 차이라고 정의 하였으므로, 이 가정에 대한 불확실성이 여전히 조건부 합성된 강우장에 포함되어 있다. 특히, 레이더 강우가 정량적으로 편차가 클수록 지상우량계로 산정된 강우분포장에 영향을 받게 되므로 기법의 한계가 존재한다. 다만 본 연구에서는 고밀도 강우관측망의 활용성 평가에 목적을 두고 강우장을 평가하고자 하여 이에 대한 불확실성에 대한 고려는 제외하였다. 추후 QPE4의 정확도 향상을 위해 호우특성에 맞는 Z-R 관계식 산정 및 보정기법을 고려하고자 한다.
3.3 교차검증
교차검증(cross validation)은 예측된 자료만을 이용하여 본래의 자료값을 다시 예측하여 예측에 사용된 방법의 타당성을 검증하는 기술로써 일반적으로 크리깅과 같은 지구통계학적 기법의 평가에 사용된다. 교차검증은 검정자료와 학습자료를 구분하는 방식에 따라 예비타당법(holdout validation), 무작위 부분추출법(random subsampling), K-중첩 교차검증법(K-fold cross validation), 잭나이프법(leave-one-out cross validation, Jack-knife) 등으로 구분된다. 본 연구에서는 각 실황 강우장 산정기법별 능력의 비교를 위해서 K-중첩 교차검증법을 적용하였다. K-중첩 교차검증법은 전체자료들을 K개로 나눈 후 한 집합을 검증집합, 나머지를 학습집합으로 만든 후 K개의 세트로 실험 진행 후 평균값으로 분류결과를 검증하는 방법이다. 무작위 부분추출법과 비슷하나 학습과 검증과정에 전체자료를 모두 이용할 수 있다는 장점이 있다. 특히 구분되는 fold의 수가 작을수록 계산이 빨라지며, 일반적으로 K =10으로 두고 수행한다. 이러한 교차검증을 통해서 K개만큼의 지점에서의 계산 값과 원 참값을 비교하여 추정오차를 계산한다. 본 연구에서는 K-겹 교차검증 K를 10으로 하여 전체 비교되는 지상강우 관측지점 190개 중에서 19개씩 임의 추출하여 10개의 집합으로 구분하였다. 단, QPE1과 같이 기상청 AWS만을 이용한 경우는 분석가능한 총 관측소 수가 34개이므로 3개씩 추출하여 10개의 집합으로 구분하였으며, 그 결과는 Table 2와 Table 3에서 괄호로 구분하였다. 관측소의 임의 추출은 랜덤하게 추출되게 하며, 동일한 집합 내에 관측소가 중복되지 않도록 하고 모든 관측소를 최대한 사용할 수 있도록 구성하였다. K의 횟수에 따라 각 호우사례별 10번씩 연산과정을 거쳐 연산과정에 포함되지 않은 관측지점의 강우량을 예측하고, 실제 관측강우를 통해 검정을 수행하였다.
추정오차를 정량적으로 계산하기 위해서 본 연구에서는 상관계수(correlation coefficient: C-CORR), 평균제곱근오차(root mean square error: RMSE), 평균오차(mean error: ME), 평균절대오차(mean absolute error: MAE)를 계산하였다. 평균제곱근오차는 추정치와 관측치의 차이를 제곱근하여 평균을 취한 것으로 편의(bias), 분해능 (resolution), 불확실성(uncertainty)에 따라 좌우되는 강우추정 정확도의 척도로 가장 많이 사용되는 요소이다. RMSE는 작은 오차보다 큰 오차에 더 큰 영향을 미친다. 상관계수는 추정치와 관측치 간차이의 일치성을 측정하는 계수이며, 평균오차는 과대추정 혹은 과소추정 양상 즉 편향 정도를 파악할 수 있으며, 평균절대오차는 오차의 크기를 판단할 수 있다(Park, 2009).

Statistics of Time series analysis between the cross validation estimates and rain gauge observations.
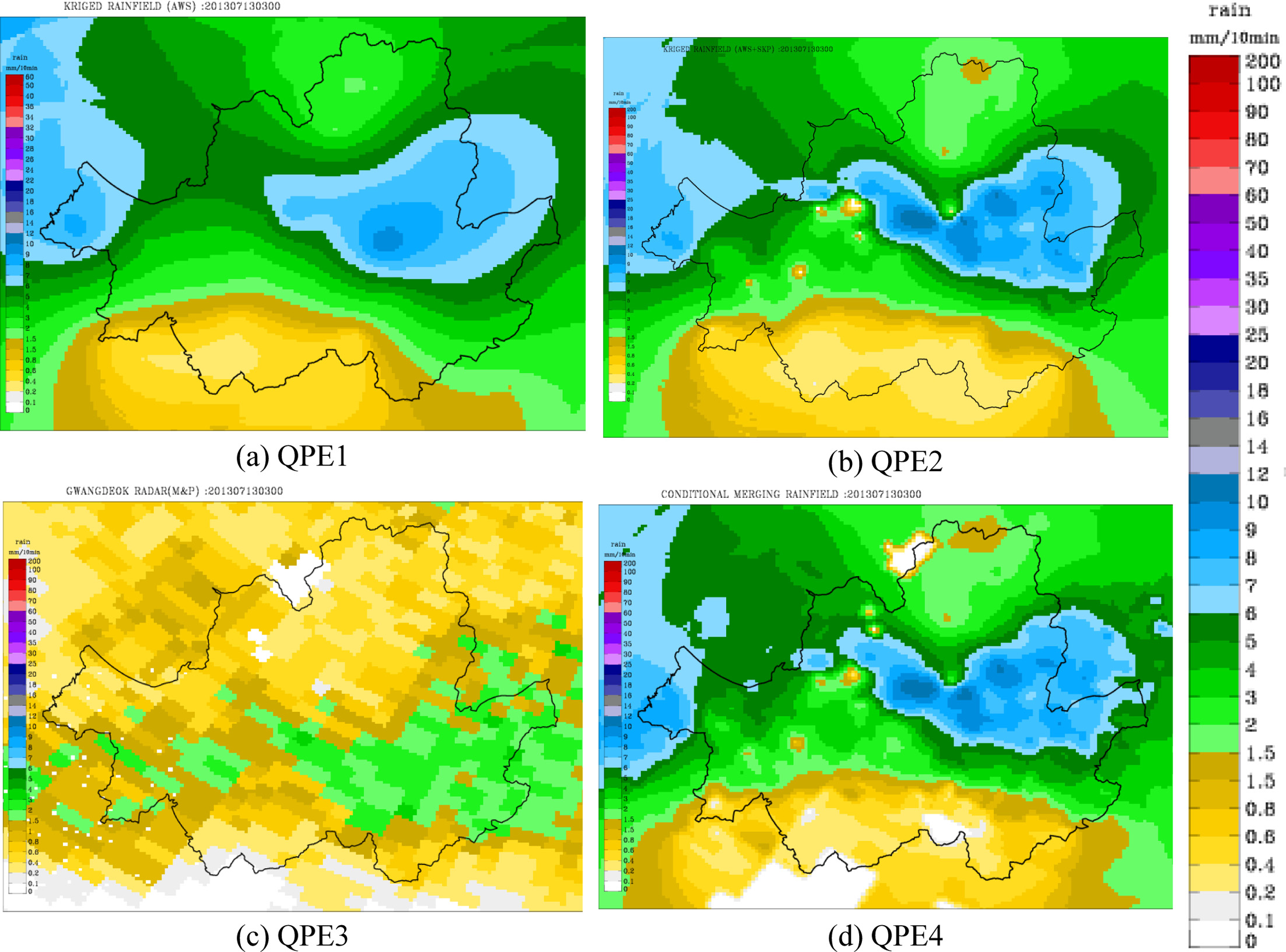
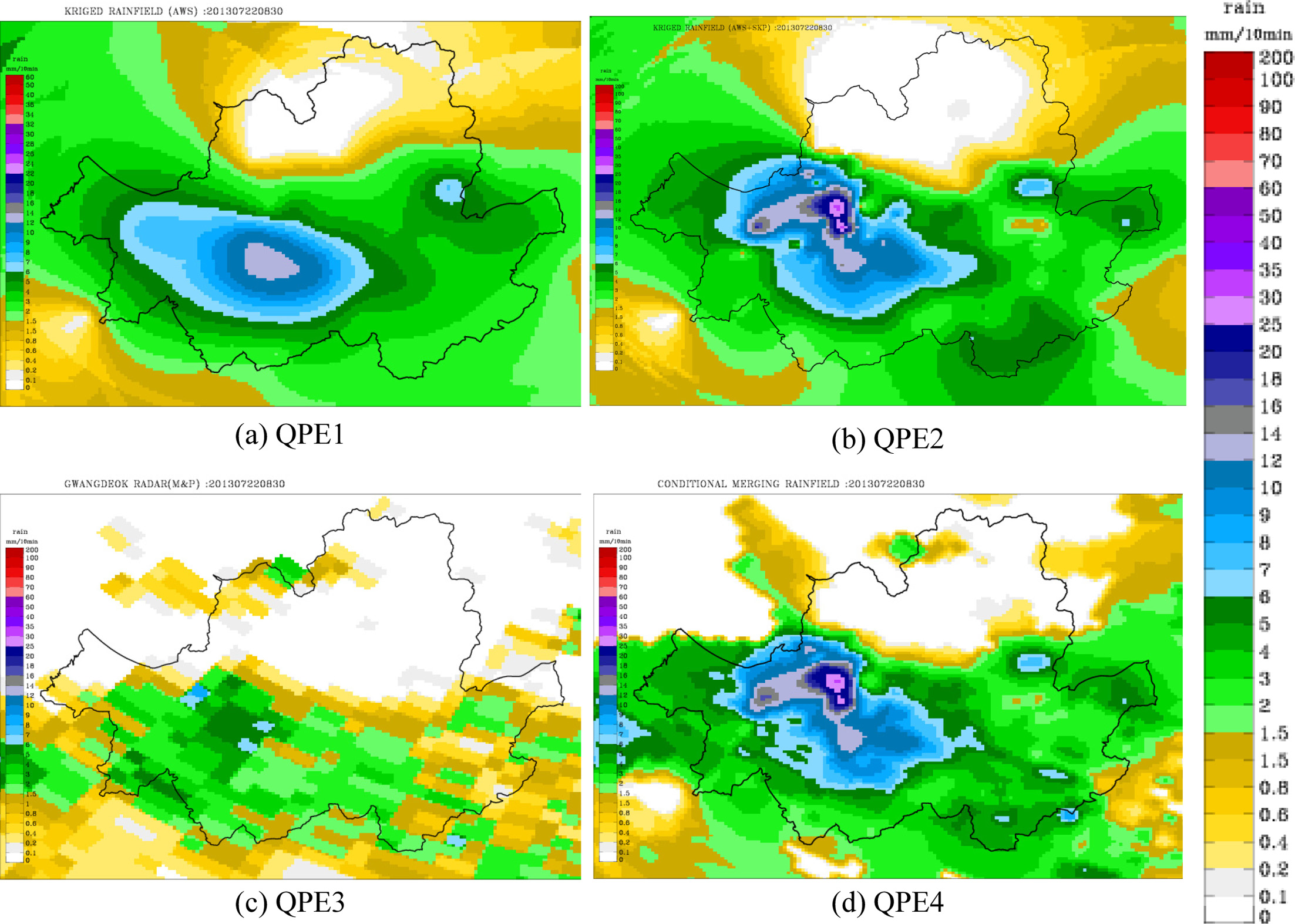
The rainfall distribution determined at 0300 LST 13 July 2013 (Case 1) using the quantitative precipitation estimation methods: (a) QPE1 using the kriging method and only information from KMA’s rain gauge network, (b) QPE2 using the kriging method and a combination of the KMA’s and SK Planet’s rainfall gauge networks, (c) the Gwangdeok-San radar rainfall (QPE3) using the Marshall-Palmer equation; (d) QPE4 using the conditional merging method.
4. 적용결과
본 연구에서는 2013년 7월 12~15일(Case 1), 7월 22일(Case 2)의 호우사례를 대상으로 매 10분 간격으로 강우분포장을 생성하였다. 호우사례 중 최대강우가 발생한 시점의 실황강우장을 Fig. 3과 Fig. 4에 도시하였다.
Figure 3은 2013년 7월 13일 03:00 (Case 1) 의 실황강우장 산정 결과이다. Figure 3a는 기상청 AWS 34개소의 관측강우를 입력자료로 정규크리깅을 적용하여 실황강우장(QPE1)을 산정한 결과로서, 대체적으로 공간적으로 평활화되면서 관측소를 중심으로 강우가 분포되는 Bull’s eye가 나타나는 양상을 보이고 있다. Figure 3b는 기상청 AWS 34개소, SK 플래닛 156개소의 관측강우를 입력자료로 정규크리깅을 이용하여 실황강우장(QPE2)를 산정한 결과이다. 그림에서 보이는 바와 같이 강우강도는 QPE1과 비슷하나, 강우분포의 패턴 및 미세한 부분의 표현에서 차이가 난다. 특히 강북지역에서 발생한 호우 중심을 QPE1에서는 동심원 형태로 강우분포를 표현하는 것에 반해 QPE2는 가로로 긴 형태의 강우분포양상을 보여 주고 있다. 다만, QPE2 역시 공간적으로 평활화되는 경향을 보이는데 이는 크리깅이 최소오차회귀분석 방법론의 일종이기 때문에 미계측 지점에서 분산을 최소로 하는 방향으로 값을 추정하기 때문이다(Yoon, 2011). Figure 3c는 광덕산 레이더 반사도를 Z = 200R1.6 식으로 강우강도로 변화하여 산정한 결과(QPE3)이며, 공간분해능은 250 m이다. 레이더 강우분포는 AWS의 관측강우를 분포시킨 것보다 현실성 있는 강우의 공간분포 양상을 보였으나, 지상우량계의 관측강우를 이용하여 분포시킨 것과 강우량 차이가 크게 나타났다. 이는 층운형 강우에 일반적으로 사용되는 Marshall-Palmer식을 사용하였기 때문에 과소 추정되었을 것이라고 판단된다. Figure 3d는 기상청 AWS와 SK 플래닛을 이용하여 산정된 실황강우장과 광덕산 레이더 강우장을 조건부 합성한 결과이다. 산정된 강우장은 강우량의 양적인 크기를 지상관측 강우와 유사하게 유지하면서 평활화된 경향이 감소하여 강우의 공간적인 비균질성을 대체적으로 잘 모의하고 있는 것으로 판단된다. 다만, 광덕산 레이더 강우 자체가 과소하여 Eq. (7)의 εR(s) 역시 작아져, 합성강우장(M(s)) 산정 시 지상관측강우로 산정된 GK(s)에 치우치는 경향이 나타나고 있다. 이는 Eq. (6)의 R(s)의 정량적 정확도를 향상시킴으로써 개선될 수 있다.
Figure 4는 2013년 7월 22일 8:30 (Case 2)의 실황 강우장 산정 결과이다. Figure 4a의 결과, 강우 중심의 위치와 강도 등 공간분포는 다르지만 Case 1의 결과와 유사하게 QPE1은 강우장이 평활화되는 것을 확인할 수 있었다. QPE2 (Fig. 4b)는 강한 강우강도를 갖는 강우 중심이 서울 강서지역에서 뚜렷하게 나타났으며, 강우분포 양상이 지역적인 집중호우 특성을 보여주고 있다. Figure 4c는 여전히 강우량의 차이가 지상강우관측에 비해 과소추정되고 있으나, QPE1과 QPE2가 공간분포기법으로 강우가 분포가 되기 때문에 실제 강우역이 레이더 강우역(QPE3)과 차이가 있다. Figure 4d를 보면, 강우량의 양적인 크기가 지상 관측 강우와 유사하며 평활화된 경향이 감소하는 것을 보이고, 강우가 존재하는 영역이 실제 레이더 영역과 유사해짐을 확인할 수 있다.
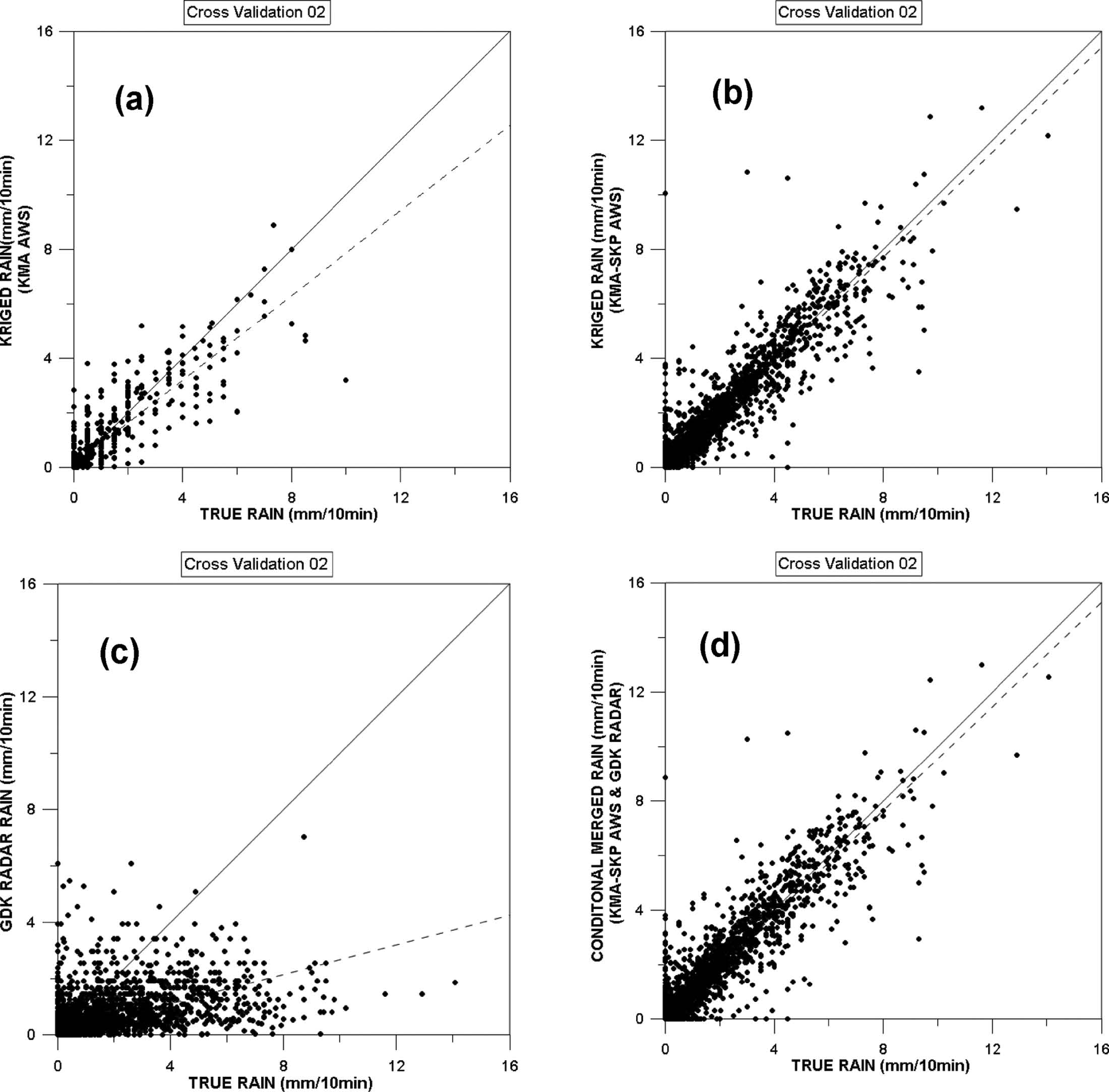
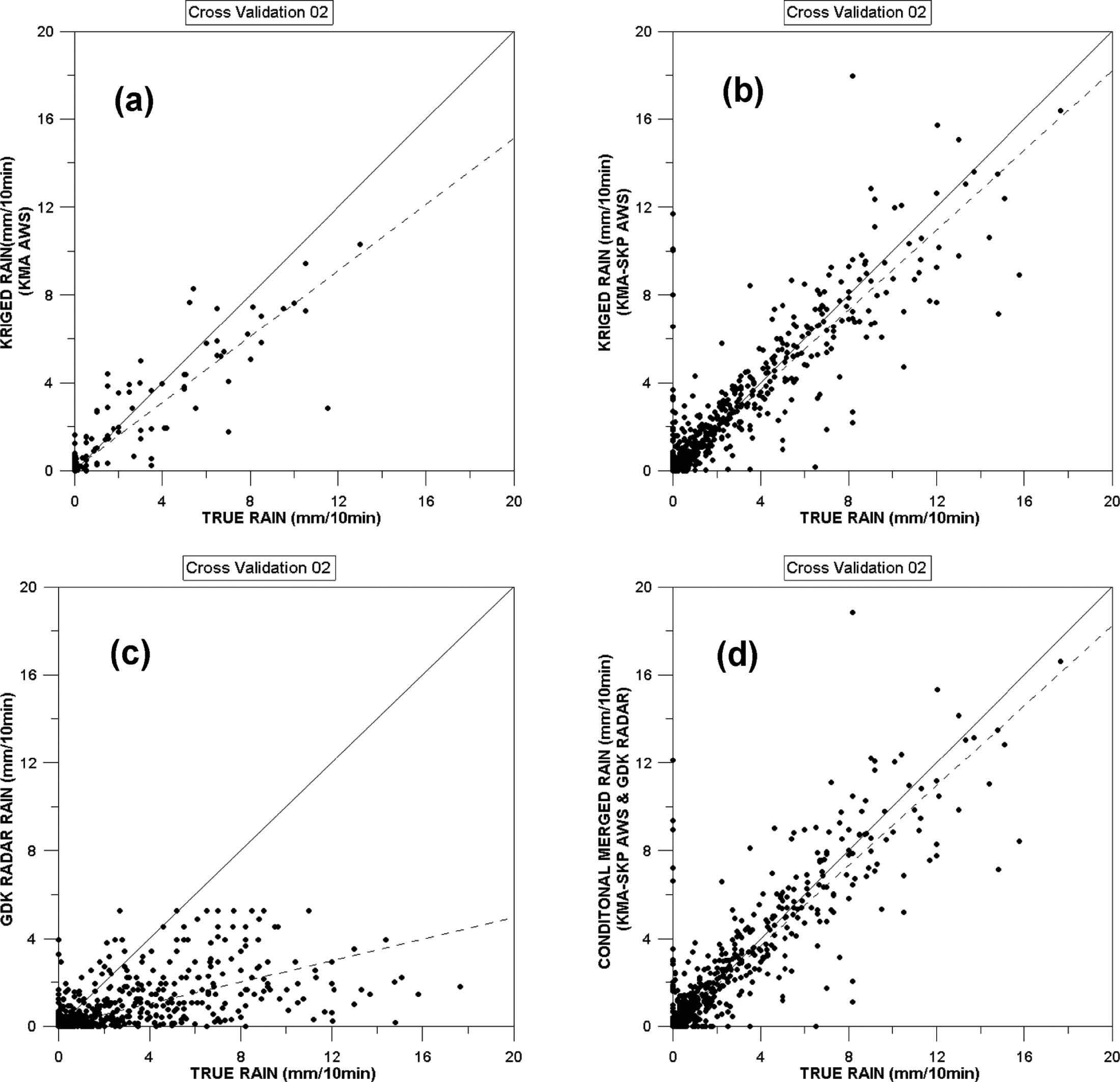
Scatter diagrams of observed gauge, raw radar, and adjusted radar rainfall intensity using 4 quantitative precipitation estimation methods for Case 1 by cross validation: (a) QPE1 using the kriging method and only information from KMA’s rain gauge network, (b) QPE2 using the kriging method and a combination of the KMA’s and SK Planet’s rainfall gauge networks, (c) the Gwangdeok-San radar rainfall (QPE3) using the Marshall-Palmer equation; (d) QPE4 using the conditional merging method.
다음 Figs. 5~6은 두 호우사례를 대상으로 교차검증에 이용된 자료들 중 임의 강우관측소 자료를 추출하여 지상관측강우와 각 실황강우장들 간의 산점도(scatter plot)를 작성한 것이며, Table 2는 이를 통계적으로 분석한 결과이다. 우선 광덕산 레이더 강우장(QPE3)에 대한 분석인 Figs. 5c와 6c의 산점도를 보면 분포가 45o 선 (실선) 아래에 치우쳐져 있고, Table 2에 정리된 바와 같이 상대오차가 -0.23과 -0.41로 레이더 강우가 과소 추정되고, 모든 통계지표에서 다른 실황강우장에 비해 가장 부정확한 결과를 보였다. QPE1의 경우 (Figs. 5a와 6a), QPE3보다는 45?선과 회귀선(점선)의 인접해 있고, 평균제곱근오차가 0.54와 0.97로 산정된 실황강우장의 오차가 레이더 강우보다는 좋은 것을 알 수 있다. Figures 5b와 6b는 고밀도 관측망을 이용하여 산정한 실황강우장인 QPE2의 경우로 45o 선에 더 밀도 있게 모여 있고, 평균제곱근오차가 0.34와 0.69로 검증관측소와의 편차가 가장 작아 고밀도 지상강우관측망을 이용하면 정확한 실황강우장을 생성할 수 있음을 확인하였다. 또한, 조건부 합성된 QPE4 (Figs. 5d와 6d) 역시 평균제곱근 오차가 0.37과 0.72로 편차가 작은 것을 확인 할 수 있었다. 상관계수는 QPE2와 QPE4가 0.93~0.95로 모두 QPE1과 QPE3에 비해 지상관측강우와 유사하게 모의됨을 정량적으로 확인할 수 있었다. 특히, 큰 차이는 없으나 QPE2의 결과가 QPE4에 비해 약간 우세함을 알 수 있었다. 이러한 영향은 레이더 실황강우장 산정에서 발생할 수 있는 부정확성이 조건부 합성시에도 영향을 미쳐 QPE4의 정확도를 다소 저하시킨 것으로 사료된다. 다만, QPE4는 QPE2에 비해 정량적인 정확도는 떨어지지만 강우의 공간 분포의 비균질성을 잘 모의하고, 특히 평활화되는 강우영역이 상대적으로 많지 않았다. 후속 연구에서는 도시홍수예측에 필요한 초단시간 예측을 본 연구에서 산정된 실황강우장을 이용하고자 한다. 따라서, 이러한 QPE4의 결과가 특성곡선법을 통해 상미분방정식을 풀어 이류벡터를 산정하는 이류모델에 적용될 경우, 이류벡터 산정 시 해의 안정성을 유지하는 점에서 더 유용하게 활용될 수 있을 것으로 판단된다(Nakakita et al., 1996; Lee et al., 2008).
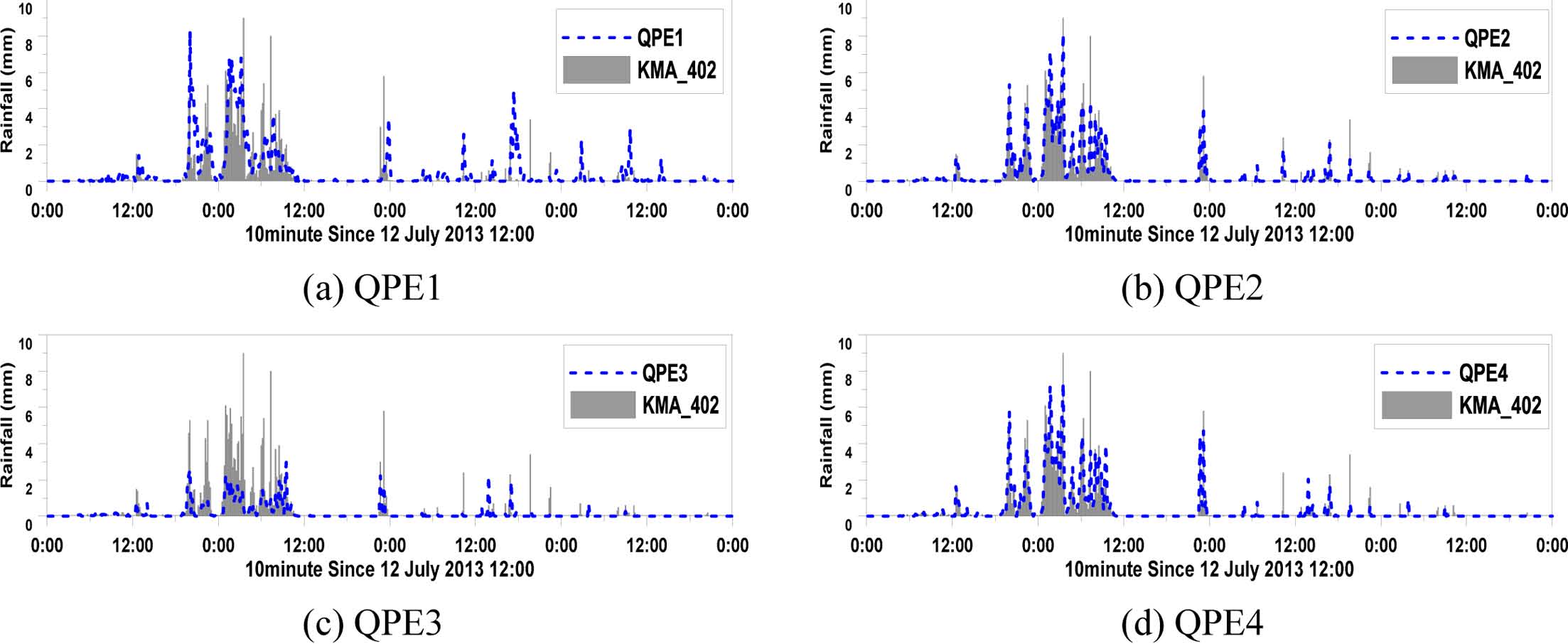
Time series of using 4 quantitative precipitation estimation methods at cross-validation station (KMA_402) for Case 1.
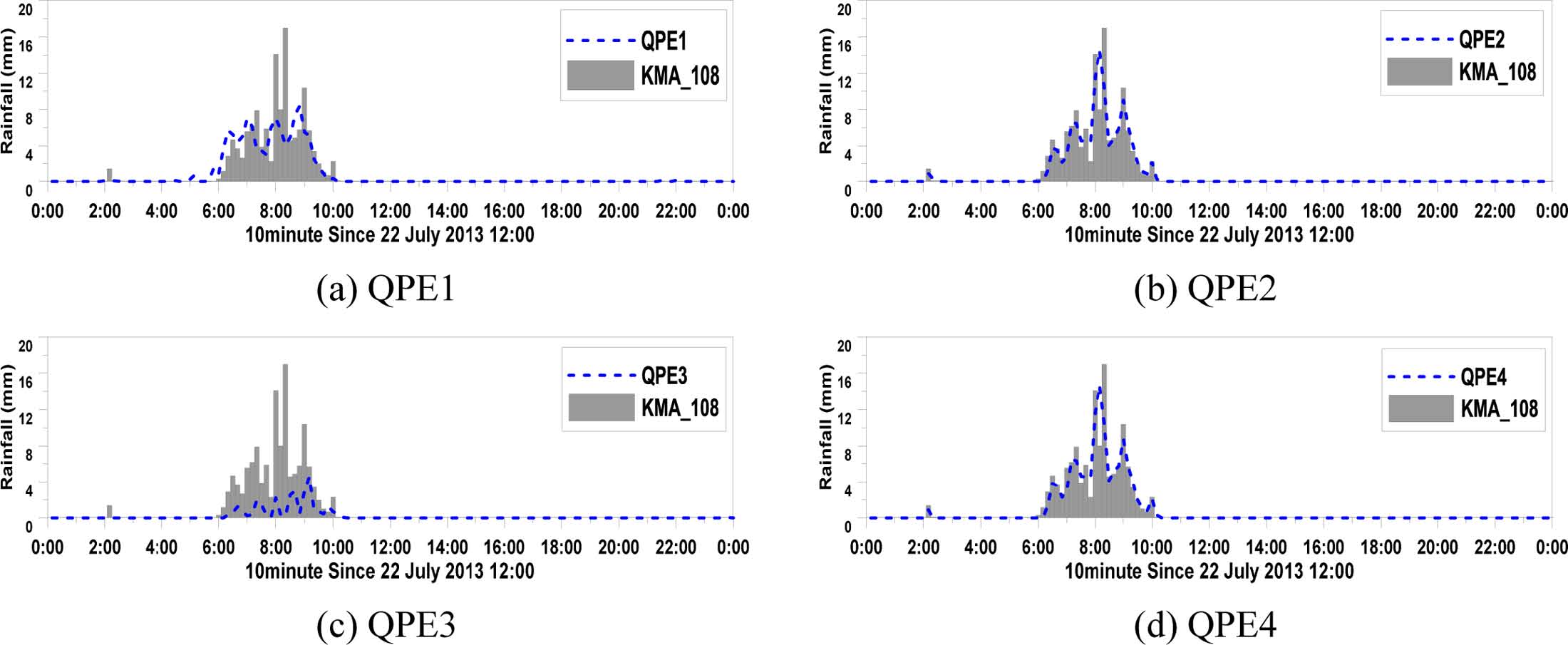
또한, 각 강우장 산정결과의 시계열 분석을 통해 정확도 차이를 확인하였다. 총 10개 fold로 구분되어 수행된 교차검증 과정에서 기상청 관측소가 사용되지 않고 산정된 강우장을 선별하여 사용되지 않은 기상청 관측소에 대응되는 격자를 추출하여 시계열로 도시하고(Figs. 7과 8), 각 호우사례별 상관계수와 평균 제곱근오차의 평균을 다음 Table 3에 제시하였다. 총 34개 관측소 시계열의 통계적 분석결과, 산포도 분석결과와 동일하게 QPE2가 가장 정확하였지만, QPE4와의 정확도 차이가 크지 않았다.
Figure 7은 Case1에 대한 기상청 강동관측소(402)와이에 대응하는 실황강우장들의 격자강우를 비교한 것이다. Figure 7a는 QPE1 비교결과로, 강우 패턴은 상관계수가 0.89로 유사하나 특정시점(7월 14일 18시경)에서 강한 강우량이 나타나거나, 평균제곱근오차가 0.3 mm (10 min)-1으로 정량적 오차가 큰 것을 알 수 있다. 이는 강우분포시 사용된 크리깅 기법과 저밀도 관측망의 한계에 기인한 것으로 볼 수 있다. Figure 7b는 QPE2의 비교결과로 산정된 강우장과 비교대상인 관측소 간의 정량적인 차이인 평균제곱근오차가 0.06 mm (10 min)-1로 0.3 mm (10 min)-1인 QPE1에 비해 작고, 검증관측소와의 상관계수가 0.97로 전체적인 강우 패턴을 잘 모의하는 것을 알 수 있다. 이를 통해 고밀도 관측망을 이용한다면 공간분포기법에 영향을 적게 받을 수 있다는 것을 알 수 있다. Figure 7d는 QPE4의 결과로서, 앞서 언급한 바대로 공간적 분포는 레이더 자료의 영향으로 차이는 있지만 정량적인 강우량은 검증관측소의 강우와의 평균제곱근오차가 0.07 mm (10 min)-1로 지상관측강우의 영향을 받아 QPE2의 결과와 유사하였다. QPE3 (Fig. 7c) 는 과소추정 경향을 뚜렷이 보여준다. Figure 8은 Case2에 대한 기상청 서울관측소 (108)의 비교결과이다. 그 결과, Case1과 유사하게 QPE2와 QPE4는 평균제곱근오차가 0.15 mm (10 min)-1와 0.16 mm (10 min)-1로 정량적인 오차가 크지 않으나, QPE1은 강우의 첨두시 오차가 크게 나타났다.
6. 결 론
도시돌발홍수 모의에 유용한 250 m 해상도의 정량적인 실황강우장을 산정하기 위해 품질 관리된 총 190개소의 지상강우관측망(기상청 AWS 34개소, SK 플래닛 156개소) 의 강우자료와 레이더 자료를 이용하였다. 2013년 7월 12~15일과 7월 22일의 호우사례를 대상으로 실황강우장을 산정하고, 교차검증과 시계열 분석을 통해 가용자료와 생산방법에 따라 구분된 4개의 강우실황장을 평가하였다. 분석호우 사례에 대해 광덕산 레이더만을 이용하여 산정한 QPE3은 정량적 정확도가 지상관측에 비해 과소 추정되었으며, 기상청 AWS만을 이용하여 산정된 QPE1의 경우 강우가 공간적으로 평활화되는 경향이 크게 나타났다. 최종적으로는 QPE2와 QPE4의 정확도가 우수한 것으로 나타났다. 특히, QPE4는 QPE2에 비해 정량적인 정확도는 떨어지지만 강우 공간 분포의 비균질성을 잘 모의하고, 특히 평활화되는 강우영역이 작아 추후 예측강우장 산정시 예측모델의 초기장으로 활용할 때, 이류벡터 산정과정에서 해의 안정성을 유지할 수 있다는 점에서 더 유용하게 활용될 수 있을 것으로 판단된다. 또한, 고밀도 관측망을 활용하면 공간분포 기법의 한계를 충분히 보완하면서 정량적으로 정확한 강우장을 산정할 수 있을 것이다. 향후 본 연구에서는 각 실황강우장을 도시지역의 홍수해석에 입력으로 활용하여 수문학적 적용성을 평가하고, 초단시간 예측모델의 입력으로 활용하여 예측강우의 정확도를 향상시키고자 한다.
Acknowledgments
본 논문의 개선을 위해 좋은 의견을 제시해 주신 두 분의 심사위원께 감사를 드립니다. 본 연구는 기상청 차세대도시농림융합스마트기상서비스개발(WISE)사업의 지원으로 수행되었습니다(KMA-2012-0001).
REFERENCES
-
Bae, D. H., J. H. Kim, and S. S. Yoon, (2005), Hydrologic Utilization of Radar-Derived Rainfall (I) Optimal Radar Rainfall Estimation, J. Korea Water Resour. Assoc., 38, p1039-1049.
[https://doi.org/10.3741/JKWRA.2005.38.12.1039]

- Ehret, U., (2002), Rainfall and flood nowcasting in small catchments using weather radar, Ph. D thesis, University of Stuttgart.
- Eom, W. G., M. L. Oh, and J. S. Jung, (1996), Mean areal precipitation estimation using radar, Proceedings of the Korea Water Resources Association Conference Korea Water Resources Association, p226-231.
- Goovaerts, P., (1997), Geostatistics for Natural Resources Evaluation, Oxford Univ. Press, New-York, 4th printing in June 2005, p483.
- Kim, B. S., J. B. Hong, H. S. Kim, and G. H. Choi, (2007), Combining radar and rain gauge rainfall estimates for flood forecasting using conditional merging method, J. Korean Soc. Civil Eng., 27, p255-265.
-
Kim, H. K., D. I. Lee, C. H. Yu, and W. T. Kwon, (2002), Radar rainfall estimation using window probability matching method : 1. Establishment of Ze-R Relationship for Kwanak Mt, DWSR-88C at Summer, 1998, J. Korea Water Resour. Assoc., 35, p211-221.
[https://doi.org/10.3741/JKWRA.2002.35.1.025]

- Lee, J. D., S. S. Yoon, and D. H. Bae, (2008), A study on the short-term forecast method using real-time on-site data, Proceedings of the Korea Water Resources Association Conference, Korea Water Resources Association, p111-114.
-
Marshall, J. S., and W. Mc. Palmer, (1948), The distribution of raindrops with size, J. Atmos. Sci., 5, p165-166.
[https://doi.org/10.1175/1520-0469(1948)005<0165:tdorws>2.0.co;2]

-
Mohr, C. G., and R. L. Vaughan, (1979), An economical procedure for Cartesian interpolation and display of reflectivity factor data in three-dimensional space, J. Appl. Meteorol., 18, p661-670.
[https://doi.org/10.1175/1520-0450(1979)018<0661:AEPFCI>2.0.CO;2]

-
Nakakita, E., S. Ikebuchi, T. Nakamura, M. Kanmuri, O. Okuda, A. Yamaji, and T. Takasao, (1996), Short-term rainfall prediction method using a volume scanning radar and GPV data from numerical weather prediction, J. Geophys. Res., 101, p26181-26197.
[https://doi.org/10.1029/96JD01615]

- Park, N. W., (2009), Comparison of univariate kriging algorithms for GIS-based thematic mapping with ground survey data, Korean J. Remote Sens., 25, p321-338.
- Pegram, G. G. S., (2002), Spatial interpolation and mapping of rainfall : 3 Progress report to the Water Research Commission, for the period April 2001 to March 2002.
-
Schilling, W., (1991), Rainfall data for urban hydrology: what do we need?, Atmos. Res., 27, p5-21.
[https://doi.org/10.1016/0169-8095(91)90003-F]

-
Sinclair, S., and G. Pegram, (2005), Combining radar and rain gauge rainfall estimates using conditional merging, Atmos. Sci. Lett., 6, p19-22.
[https://doi.org/10.1002/asl.85]

- Vieux, B. E., P. B. Bedient, and E. Mazroi, (2005), Real-time urban runoff simulation using radar rainfall and physics- based distributed modeling for site-specific forecasts, 10th International Conference on Urban Drainage.
- Yoon, S. S., (2011), Development of Optimal Radar Rainfall Estimation with Orographic Effect and Urban Flood Forecasting Application Technique, Ph. D. dissertation, Sejong University, Seoul, Korea.
-
Yoon, S. S., and D. H. Bae, (2013), Optimal rainfall estimation by considering elevation at the Han River Basin, South Korea, J. Appl. Meteor. Climatol., 52, p802-818.
[https://doi.org/10.1175/JAMC-D-11-0147.1]

- Yoon, S. S., B. J. Lee, and Y. J. Choi, (2015), Derivation of data quality control strategy for high density rain gauge network in Seoul area, J. Korea Water Resour. Assoc., (printing).