도심 확산 모의를 위한 대표 기상장 산출 방안
Ⓒ 2024 Korean Meteorological Society
Abstract
To simulate dispersion of atmospheric pollutants in urban areas, representative meteorological fields were calculated by classifying various meteorological data based on surface wind direction/speed and atmospheric stability obtained from the 5-year (2015~2019) record of ERA5 reanalysis data. Wind direction and speed were divided into 16 and 4 categories, respectively. Pasquill-Gifford (P-G) method is used to classify atmospheric stability into 3 categories for surface meteorological fields and Bulk Richardson number is used to classify atmospheric stability into 3 categories for vertical profiles. The atmospheric profiles of temperature, humidity, wind speed, and potential temperature for a given point (Seoul in this study) were grouped into the 192 (16 × 4 × 3) categories for each season. The classified atmospheric profiles represent the similarity of the group relatively well. These profiles can serve as input data for atmospheric dispersion modeling under various wind and stability conditions, providing more accurate and improved results. This approach ensures that vertical profiles accurately reflect the properties of surface data, enhancing correlation and reliability in simulation outcomes.
Keywords:
Atmospheric dispersion model, Atmospheric stability, Pasquill-Gifford, ERA51. 서 론
수십 년간 이루어진 도시의 발달로 인해 대규모 고층 건물의 건설 등으로 건물 밀집도가 높아지고 있다. 이에 따라 도시규모의 대기 순환과 오염물질 확산에 대한 관심과 연구가 꾸준히 증가해 오고 있다. 건물, 도시 규모 등의 상세 규모 대기 순환과 오염물질 확산 현상을 모의를 위해 다양한 수치해석 기반의 대기 확산모델이 이용되어 오고 있다. 그 중에서도 짧은 시간 안에 많은 인명피해를 유발할 수 있는 유해 오염 물질의 경우는 정확한 정보에 기반한 신속한 대응이 요구되므로 이를 위해 많은 국가에서 수치해석 기반의 대기확산모델이 개발 연구되었다(Stein et al., 2009; Srinivas et al., 2012; Bowyer et al., 2013; Connan et al., 2013; Jeong et al., 2013; Povinec et al., 2013). 1920년대부터 영국 및 미국을 중심으로 확산이론이 제시되고, 지금까지 많은 대기확산모델이 개발되어 현재 대기환경 영향평가 및 대기질 정책 수립에 매우 유용하게 사용되고 있다(예, Cohen et al., 2004; Chen et al. 2012; Yerramilli et al., 2012; Stein et al., 2015).
이러한 대기확산모델은 크게 간단한 유출과 확산을 가정하는 가우시안 모델(Gaussian model)과 3차원 기상장을 복합적으로 반영하는 수치해석 모델로 구분할 수 있다. 가우시안 모델은 복잡한 지형 지역에서 활용하기 어렵고 비정상상태 거동을 모의하는데 한계가 있어, 최근에는 3차원 수치해석 모델을 활용하기 위한 연구들이 많이 진행되고 있다(Bocquet, 2012; Arnold et al., 2015; Geng et al., 2018; Lee et al., 2020). 대기확산모델은 그 방법과 정확도가 매우 다양하게 구성되어 있기 때문에 사용 목적에 따라서 적절한 모델이 선정되어야 하고, 그 모델의 한계성과 적용 범위에 대해서도 정확히 이해하고 사용해야 한다.
특히 대기확산모델의 입력장으로 활용되는 기상 정보(풍향, 풍속, 기온 등)는 오염물질의 수송 및 확산에 직접적으로 기여하고, 확산의 시간변화를 고해상도로 예측하는 3차원 수치해석 모델의 경우는 그 결과가 기상장의 정확도에 민감하기 때문에 확산 상황에 적합한 기상자료 있다면 대기확산모델의 성능을 크게 향상시킬 수 있다(KEITI, 2014). 이러한 노력의 일환으로 농촌진흥청(RDA, 2010)에서는 축산악취 확산의 예측 모델의 개발을 위해 풍향, 풍속, 기온 등의 주요 기상인자들을 측정하고 대기안정도를 판단하기 위해 연직 기온분포의 관측을 시행하였다. 그 결과 확산모델의 성능 향상을 위해 보다 정확한 풍향과 풍속의 측정이 중요함을 보였고 대기안정도가 악취 분포에 가장 큰 영향을 주는 것으로 나타났다. 이처럼 대기안정도, 풍속과 풍향 등의 기상 조건은 오염물질의 대기확산에 영향을 주는 중요한 인자들이며, 다수의 연구에서 대기안정도에 따른 풍향, 난류 특성 및 기온의 연직 분포 프로파일을 개선하여 대기확산 모델의 성능을 향상시킬 수 있음을 보이고 있다(Jeong, 2021; Lee et al., 2022).
이와 같이 상세한 기상 정보(풍향, 풍속, 기온, 대기안정도)를 활용하는 3차원 수치해석 모델은 오염 물질 확산 상황을 이해하고 이에 대응하는데 중요한 정보를 제공할 수 있다. 그러나 3차원 수치해석 모델은 단순 확산모델보다 상대적으로 계산량이 많아 모든 기상 상황에 대한 활용은 아직 어려운 실정이다. 본 연구에서는 3차원 수치해석 모델을 활용하여 상세한 정보를 산출하되, 상황에 맞게 효율적으로 계산량을 조절할 수 있도록 기상장을 분류하고 각 분류별로 기상 특성이 반영된 입력자료를 새롭게 산출하였다. 풍속, 풍향과 대기안정도를 기반으로 기상장을 분류하고 연직 프로파일 정보를 산출하여 3차원 수치모델 기반의 대기확산 모델 입력자료로 사용될 수 있는 데이터베이스를 구축하였다.
2. 연구 방법
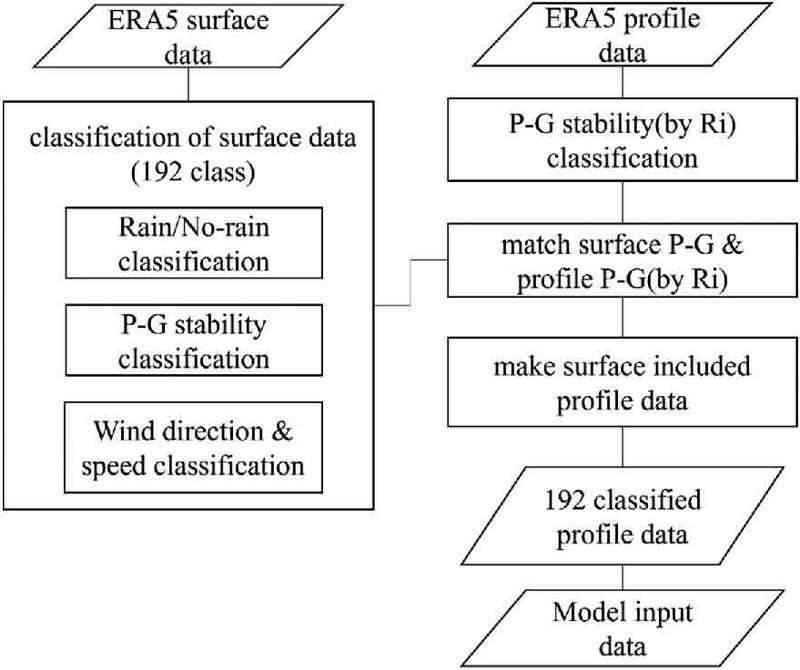
상세규모 대기확산 모의를 위한 기상장을 분류하고 연직 프로파일을 산출하기 위해 ECMWF (European Centre for Medium-Range Weather Forecasts)에서 제공하는 고해상도 재분석 자료인 ERA5 (ECMWF Reanalysis v5)를 사용하였다. 기간은 2015년부터 2019년으로 총 5년치 자료가 사용되었다. 연구 대상 지역은 광화문 세종사거리 중심을 기준으로 반경 2 km 공간이다. ERA5의 지표면 자료를 이용하여 강수 유무를 나누고 계절별 대기안정도, 풍향과 풍속을 분석하고 각 특성에 맞게 분류하였다. 그 후 ERA5 연직 프로파일 자료를 사용하여 연직 프로파일의 대기안정도 등급을 나누었다. 지표의 경우 Pasquill-Gifford 대기안정도 등급을 사용하였고 연직 프로파일의 경우에는 리차드슨 수를 사용하였다. 두 대기안정도를 매칭하고 강수 유무와 계절별로 192개로 분류된 기상 정보를 이용하여 기상장 데이터베이스를 구축하고 각각의 분류에 대한 연직 프로파일을 산출하였다. 연구 방법의 전체적인 흐름은 Fig. 1에 나타내었다.
2.1 대기확산 모델링
본 연구에서는 큰에디모사 모델 중 하나인 PALM을 이용해 오염물질의 확산을 모의하기 위해 입력자료로 사용될 기상장을 분류하고 연직 프로파일을 산출하였다. PALM은 FORTRAN (FORmula TRANslation) 언어를 바탕으로 구성되어 있으며 1997년 최초 버전이 개발된 이후로 현재까지도 개발이 지속되고 있다. 모델에 대한 광범위한 확장으로 인해 PALM은 더 이상 약어가 아닌 그 자체의 이름으로 사용되고 있다. 대기 및 해양 경계층 흐름에 대한 기상 모델링 시스템으로 다양한 도시 응용 프로그램에 모델을 사용할 수 있다. 또한 다양한 규모의 기상, 기후 현상, 복사, 도시지역 에너지, 식생, 토양, 대기 화학적 수송 등의 여러 현상에 대한 복합적인 조사와 분석이 가능하다. PALM에서는 유체의 흐름을 모의하기 위해서 유체의 운동량과 관련된 방정식을 수치적으로 풀이한다. 방정식은 각각 유체 운동량 보존에 대한 나비에-스토크스 방정식, 열에너지 방정식, 스칼라 수송방정식, 연속방정식으로 이루어져 있다(Maronga et al., 2020; Yang et al., 2021). PALM 모형은 LPM (lagrangian particle model)의 접합을 통해 난류 흐름에서의 라그랑지안 입자 확산을 계산할 수 있는 방안을 제공한다(Maronga et al., 2020). PALM에서 입력자료로 필요로 하는 정보는 지표부터 약 1 km 정도의 대기하층에 대한 변수들의 연직 프로파일 정보이다. 필요한 변수는 Table 1에 정리되어 있다.
모의 영역은 광화문 세종사거리 중심을 기준으로 반경 2 km 공간을 포함하며 모델 상단 높이는 1,168m로 설정하였다. 대상 지역의 지형과 건물 자료를 모두 반영하여 모의를 수행하였다. 지형 자료는 국토지리정보원의 연속수치지도2.0 등고선 자료를 불규칙 삼각망(triangulated irregular network, TIN) 보간법을 이용하여 모의 영역 내 지형 정보를 구성하였으며, 건물 자료의 경우 국토지리정보원의 연속수치지도 2.0의 건물 레이어 자료를 이용하여 층수 및 평균 층고 3 m를 적용하여 기본 구성을 하고, 브이월드(VWorld)에서 건물 높이가 제공되는 건물에 한해서만 건물 높이 정보를 업데이트 하여 건물 높이 정보를 사용하였다. 수평 및 연직 격자 크기는 각각 10 m와 3 m이며, 고도 336 m 이상의 연직 격자 크기는 1.08 비율로 증가한다. 수치 적분은 5,600초이며 스핀업 시간 1,800초를 포함하고 모의 결과는 10분 간격 평균바람과 농도값으로 산출한다.
입자 방출은 모의 영역의 중심인 세종사거리에서 발생하는 시나리오에 따라 설정하였다. 입자 방출은 지표에서 단일 격자 크기(10 × 10 × 3 m3)의 공간에 균일한 입자 분포로 순간 방출로 이루어지며, 방출 시점은 모형 스핀업 시간인 1800초 이후에 시작된다. PALM-LPM 모형 설정 값은 Table 2에 정리되어 있다.
2.2 ERA5
ERA5는 유럽 중기기상예보센터의 최신 재분석자료로 고해상도 모델에 가용한 모든 지상, 고층(존데, 항공기), 위성 자료를 동화하여 기상정보를 최적 추정한 자료이다. 한국의 LDAPS (local data assimilation and prediction system)에 비해 수평 해상도는 낮으나 시간해상도가 높고(1시간), 장기간의 분석 데이터를 높은 정확도로 제공하며 대기의 중요 상태 변수(바람, 온도, 습도, 안정도, 오존 등)를 수평 ~25 km, 연직 ~250 m의 격자 해상도로 제공(Hersbach et al., 2020)하고, 중규모 및 미규모의 기상 및 대기확산 연구에 활용도가 높다(Mun et al., 2020). 본 연구에서는 기압고도(pressure level) 자료를 활용하여 대기의 동서바람(u), 남북바람(v), 온도(T), 습도(q, specific humidity) 정보를 고도에 따라 산출하고, 리차드슨 수를 활용하여 연직 대기안정도를 산출하였다. 해당 자료는 확산모델링을 수행하고자 하는 모든 지점에서 활용이 가능하며, 추후에 해당 기법의 활용성 및 지상관측(automated synoptic observing system, ASOS)과의 상관성을 분석하기 위해 ASOS 서울(108) 관측지점과 가장 가까운 37.50oN, 127.00oE 격자의 정보가 사용되었다.
2.3 Pasquill-Gifford 대기 안정도 등급
대기의 확산계수는 바람장 연직 정보와 함께 물질의 확산 및 이동에 중요한 역할을 하지만, 실제로 이값을 측정하는 것은 매우 어려운 과정이다. 3차원 초음파 풍향풍속계를 이용하여 확산계수를 추정하는 방법이 있지만, 이는 장비의 유지와 운영에 높은 전문성이 필요하여 다수의 관측소에서 활용하기 어려운 문제가 있다. 확산계수는 거리에 따른 대기안정도 함수 등으로 추정되고 전통적으로 Pasquill-Gifford 곡선을 기반으로 한다(Hwang et al., 2013). Pasquill-Gifford (P-G) 분류 방법은 지상 풍속, 일사량 및 구름의 양과 같은 변수들을 활용하여 대기안정도를 분류하는 방법으로, 이는 Pasquill과 Gifford가 1961년에 제안하였으며(Gifford, 1961; Pasquill, 1961) 현재까지 많은 연구에서 사용되고 있다(Nakajima et al., 2020; Park et al., 2023). P-G 대기안정도 분류 방법 중 주간 일사량의 경우 강, 중, 약으로 나뉘는데 여기서는 Seinfeld and Pandis (2006)에서 사용한 일사량 기준을 이용하였으며 자세한 내용은 Table 3에 정리하였다. 본 연구에서는 재분석 자료에서 얻은 지표 정보만을 활용하여 P-G 방법을 사용하여 대기확산의 등급을 분류하였다. 대기안정도를 극히 불안정부터 안정까지 총 9등급(A, A-B, B, B-C, C, C-D, D, E, F)으로 나눈다. A에서 F로 갈수록 대기의 안정도가 높아진다(Table 4). 해당 방법론은 한반도 지역에서도 적용되어 합리적인 결과를 도출하는 것으로 알려져 있으며 주요 도시에서는 안정 조건의 대기가 불안정 조건보다 더 많이 발생하는 것으로 알려져 있다(MAMO, 2011). Seinfeld and Pandis (2006) P-G는 대기안정도를 9개의 등급으로 나누었는데 본 연구에서는 지표 자료 분석을 통해 안정, 중립 그리고 불안정 3등급으로 분류하였다. 2.5 절에서 지표의 풍향, 풍속과 함께 대기안정도에 대한 분석이 이루어질 것이다.

Pasquill-Gifford stability classification table based on solar radiation, cloud cover, and wind speed (Seinfeld and Pandis, 2006).
2.4 리차드슨 수
P-G 대기안정도는 일사량이 유일한 가열 근원으로, 기온의 연직 구조에 관계없이 대기안정도를 추정하기 때문에 상층의 대기안정도를 판별하기에는 부정확한 단점이 있다(Kim et al., 2005). 따라서 본 연구에서는 지표의 대기안정도는 P-G 방법으로 구하였다면 연직 대기 안정도는 동적 안정도 중 하나인 리차드슨 수(bulk Richardson number, Ri)를 이용하여 구하였다. Ri는 난기류의 지표이자 안정성의 지표로서 연직 대기안정도를 필요로 하는 연구에 많이 사용되고 있다(Oh et al., 2020). Ri는 변수로 연직 온위의 기울기와 함께 연직 풍속의 기울기를 사용한다. Ri는 아래 식(1)부터 식(5)를 이용해 구할 수 있다. T200과 T2는 각각 고도 200 m와 2 m에서의 온도이다. T2는 ERA5에서 제공하는 지표에 가장 가까운 온도로 본 연구에서는 지표 온도로 사용하였다. 온위인 θ2도 마찬가지로 지표 온위로 사용되었고 θ200는 200 m에서의 온위이다. 마지막으로 u200와 u10는 각각 200 m와10 m에서의 풍속인데 u10을 지표에서의 풍속으로 사용하였다.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
일반적으로 Ri는 안정적인 대기 조건에서는 큰 양의 값을 가지고 불안정한 대기 조건에서는 음의 값을 갖는다. 본 연구에서는 Leelőssy et al. (2014)에서 정리한 Ri 값과 이에 해당하는 P-G 대기안정도를 사용했다(Table 5). Ri가 -0.86보다 작을 때는 A, -0.86보다는 크고 -0.37보다는 작을 때 B, -0.37보다 크고 -0.10보다 작을 때 C, -0.10과 0.053 사이의 값을 가질 때는 중립인 D, 0.053과 0.134 사이의 값을 가질 때는 E, 그리고 마지막으로 0.134보다 큰 값을 가질 때는 F로 분류된다. 다음 절에서 지표의 특성분석을 통해 Ri와 P-G 대기안정도를 새롭게 분류할 것이다.
2.5 바람장 및 안정도 기반 분류
앞서 언급했듯이 도시 규모에서 대기오염물질의 상세 순환 및 확산을 모의하는데 있어서 기상정보는 필수적인 사항이며 그 중에서도 특히 풍향, 풍속과 대기안정도는 대기확산 모델링에 큰 영향을 미치는 중요한 인자이다. 이번 절에서는 이 세가지 기상정보의 특성에 따라 ERA5 지표 자료를 어떻게 분류할 것인지 다룰 것이다.
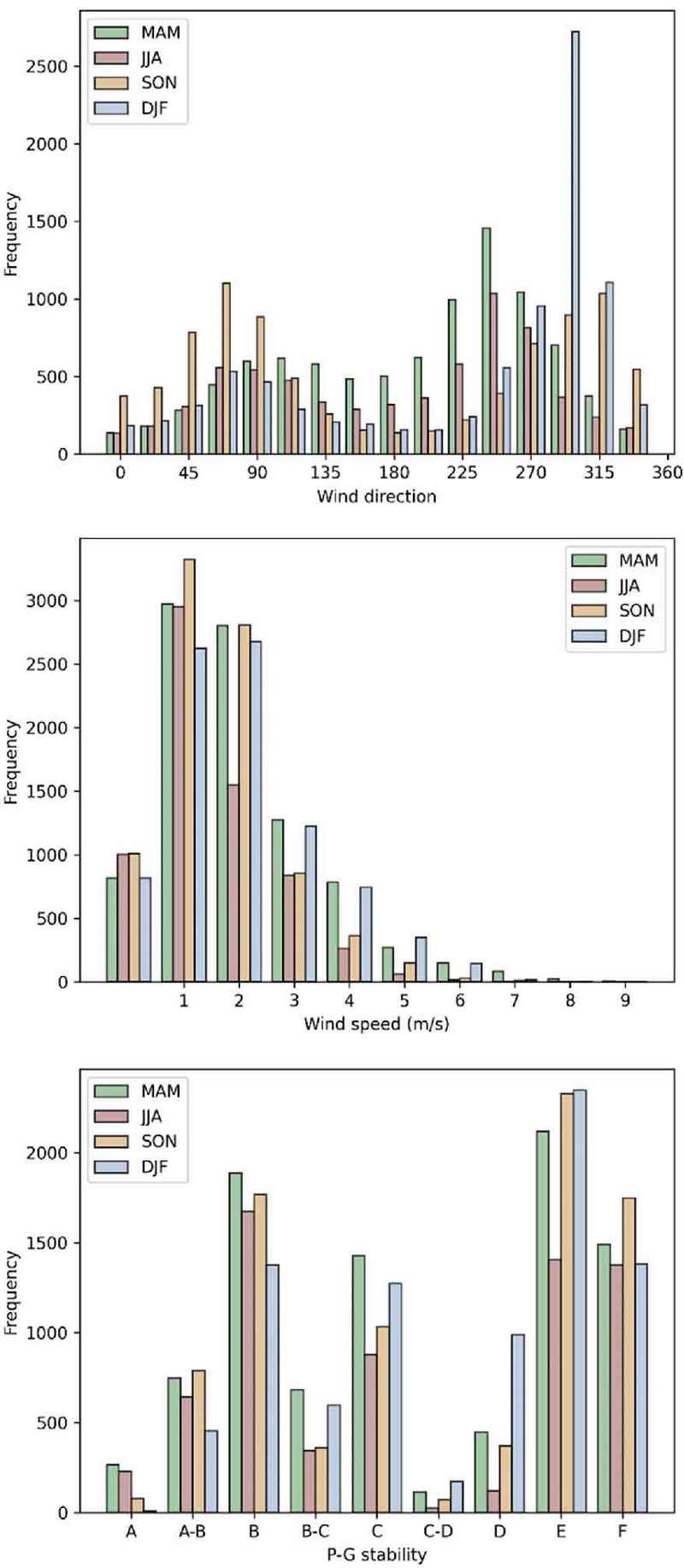
Figure 2는 맑은 날(비가 오지 않는 날) 계절별 풍향, 풍속과 대기안정도의 빈도 분포를 나타내었다. 먼저 풍향의 경우, 전체적으로 서풍과 동풍 계열이 우세한 경향을 보이고 계절별로는 조금씩 차이가 있다. 겨울의 경우 북서풍이 다른 계절에 비해 매우 우세한 경향을 보이고 있다. 또한 가을엔 북동풍 계열이 다른 계절에 비해 우세한 모습을 보이고 있다. 봄과 여름에는 남서풍 계열이 우세하고 빈도는 봄에서 가장 크게 나타난다. 이러한 하층의 풍향 구조는 관측소 주변의 국지적인 지형조건에 크게 영향을 받는다. 풍향의 지표 특성에 기반하여 정북을 기준으로 22.5o 간격으로 총 16단계로 분류하고 각각 WD01부터 WD16로 명칭을 정하였다.
다음으로 풍속의 경우, 계절별로 1 m s -1 단위로 빈도를 구하였다. 빈도 분포를 봤을 때 풍속은 0~2 m s-1 구간까지는 빈도가 증가하다가 그 이후에는 점점 감소하기 시작하여 6 m s-1 이상의 강한 풍속은 빈도가 매우 낮은 것을 알 수 있다. 1 ~2 m s -1 구간에서 가을에 특히 해당 구간의 풍속의 빈도가 높은 것을 알 수 있다. 2 m s-1 구간을 넘어가면서부터 다른 계절에 비해 여름일 때 빈도가 확연히 줄어드는 모습을 보인다. 풍속이 낮은 경우 오염 물질의 확산 속도가 줄어들어 배출원 근처의 농도가 상승하게 되는 등 오염물질의 대기확산을 모의하는데 있어서 풍속의 역할은 매우 중요하다(Park et al., 2005). 풍속은 빈도 분포를 고려하여 가장 약한 구간(0~1 m s-1) WS01, 중간 구간(1 ~3 m s -1) WS02, 강한 구간(3~5 m s-1) WS03과 매우 강한 구간(5 m s-1 이상) WS04로 총 4개로 분류하였다.
마지막으로 P-G 대기안정도 등급의 전체적인 빈도 분포를 보면 안정 등급인 E가 가장 많은 부분을 차지하고 있는 것을 알 수 있다. 그 다음으로 불안정 등급인 B가 우세하고 그 뒤를 이어 F와 C 등급도 높은 빈도를 보인다. A와 C-D는 상대적으로 작은 값을 나타내고 있다. 다만 계절별로는 차이가 보이는데 여름에는 E와 F의 빈도가 비슷하고 B의 빈도가 훨씬 높게 나타난다. 이는 주간 일사량이 높은 여름 특성상 B의 빈도가 가장 높게 나타나는 것으로 판단된다. 이러한 분포를 바탕으로 P-G 대기안정도는 9개 등급에서 A, A-B, B, B-C, C와 C-D를 묶어 불안정, D와 E를 묶어 중립, F는 불안정으로 정하여 대기안정도 등급을 새롭게 3등급으로 분류하였다. 지표의 특성을 반영하여 3등급으로 새롭게 분류한 P-G 대기안정도와 Ri를 Table 6에 나타내었다. Ri가 -0.10보다 작은 값을 가질 때는 불안정(PG01), -0.10보다는 크고 1.34보다는 작은 경우는 중립(PG02), 그리고 0.134보다 큰 경우는 안정(PG03)이다.
정리하면, ERA5 지표 자료의 분석을 바탕으로 풍향은 정북을 기준으로 22.5o 간격으로 나누어 16단계, 풍속은 약함, 중간, 강함과 매우 강함으로 총 4단계, 대기안정도는 불안정, 중립과 안정 3단계로 등급을 정하였다. 풍향, 풍속과 대기안정도의 특성에 따라 기상장을 계절별로 총 192개의 등급으로 분류할 수 있다. 자세한 내용은 Table 7에 정리하였다.
2.6 연직 기상자료
ERA5는 지표 자료뿐만 아니라 1,000 hPa 부터 40개 층으로 이루어진 연직 기상 자료를 제공한다. 확산 모델링에 필요한 정보는 지표부터 약 1 km 정도의 대기하층에 대한 연직 프로파일 정보이다. 이에 맞는 자료를 생산하기 위해 먼저 기압(hPa)을 기준으로 생산된 자료를 고도(m 단위)를 기준으로 하는 자료로 변환한다. 다음으로 ERA5 지표 자료와 연직 프로파일 자료를 연결해주는 작업이 필요하다. 연직 프로파일 자료의 가장 하단인 1,000 hPa의 자료의 고도를 비교하여 지표 자료를 내삽 또는 외삽하여 연직 프로파일에 지표 자료를 추가하였다. 이렇게 하면 지표부터 시작하는 연직 프로파일 자료를 생산할 수 있다.
P-G 대기안정도 등급을 이용해 분류한 지표 자료와 Ri를 이용해서 분류한 연직 프로파일의 대기안정도 등급을 비교하여 일치하는 경우만 분석에 사용하였다. 즉, Table 6에 나와 있는 내용을 바탕으로 P-G 대기안정도 등급이 A에서 C 사이일 때 Ri가 -0.10보다 작은 경우(PG01), P-G 대기안정도 등급이 C-D에서 E 사이일 때 Ri 값이 -0.10보다 크거나 같고 1.34보다 작은 경우(PG02), 마지막으로 P-G 대기안정도 등급이 F 일 때 Ri가 0.134보다 크거나 같은 경우(PG03)만 분석에 사용하였다. 이 세 가지의 경우는 전체 사례의 54%를 차지하였다. 이렇게 함으로써 지표와 연직프로파일의 연관성을 높여 보다 정확한 대기확산 모델의 입력자료를 생산할 수 있다. 지표와 연직 프로파일을 매칭한 대기 안정도를 PG01, PG02, 그리고 PG03으로 나타내었다.
3. 결 과
3.1 산출된 대기확산모델 입력자료의 특성 분석
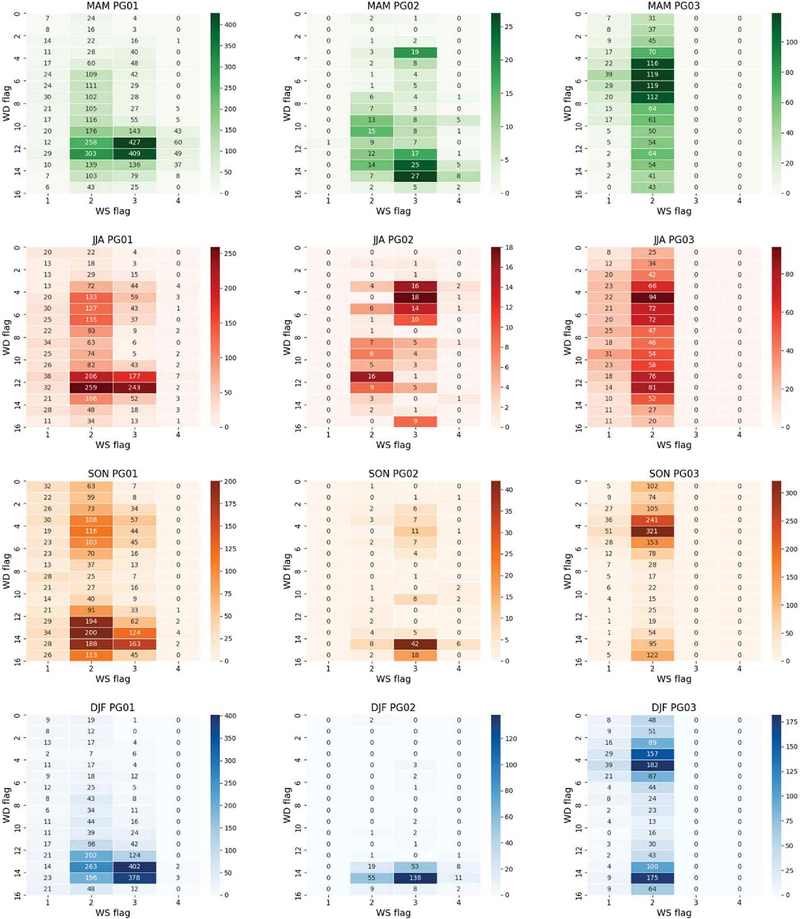
Figure 3은 대기안정도 등급에 따른 계절별 지표 풍향과 풍속의 분포를 나타낸 것이다. 각 계절별로 색깔이 진해질수록 높은 빈도를 가지는데 전체적으로 봤을 때 풍속은 WS02와 WS03에 많이 분포하고 있고 풍향은 WD05와 WD13 근처에 많이 분포하고 있다. 대기안정도 등급별로 자세히 보면, PG01의 경우 봄과 겨울에는 WD13과 WD14 근처에서의 빈도가 높게 나타나고 여름과 가을에는 WD05 근처에서의 빈도도 높게 나타난다. 대기가 불안정한 경우(PG01), 모든 계절에서 서풍 계열(WD13)이 우세하고 여름과 가을에 동풍 계열(WD05)이 나타나는 모습이다. 대기안정도가 중립(PG02)일 때는 모든 계절에서 그 빈도가 다른 때에 비해 낮게 나타나는 것을 알 수 있고 특히 겨울에는 그 빈도가 WD15WS03에 몰려 있는 것을 알 수 있다. 대기가 안정한 경우(PG03)을 보면 WS02에 주로 분포하고 WS01에도 작지만 어느 정도 분포하고 있는 모습을 볼 수 있다. 대기가 안정한 경우 풍속이 작은 값을 가지는 것을 알 수 있다.
지표와 연직 프로파일의 대기안정도를 매칭한 각각의 PG 등급에 대해 온도, 온위, 습도와 풍속의 연직 프로파일 분포를 Fig. 4와 Fig. 5에 나타내었다. 각 색깔은 계절별 연직 프로파일의 68% (μ ± σ, μ와 σ는 각각 계절별 연직 프로파일의 평균과 표준편차)를 나타내고 실선은 평균값이다. 일반적으로 온도와 온위는 여름에 가장 높은 값을 가지고 겨울에 가장 낮은 값을 갖는 계절성을 매우 뚜렷하게 나타내고 있으며, 봄과 가을은 절대적인 값은 유사하지만 전반적으로 가을이 더 높은 값과 변동성을 보인다. 불안정한 등급인 PG01에서 지표부근에서 온위가 높은 값을 가지다가 고도에 따라 감소하는 모습을 보이고 안정한 등급인 PG03에서는 지표에서 상층으로 갈수록 온위가 증가한다. 다만 100 m 이상의 상층에서는 모든 등급에서 고도에 따른 온위의 변화가 지표 부근만큼 크게 나타나지는 않는다. 고도에 따라 온위가 증가하면(dθ/dz > 0) 대기는 안정하고 반대로 온위가 감소하면(dθ/dz < 0) 대기는 불안정하다. PG 등급과 고도에 따른 온위의 변화가 잘 일치하는 것을 알 수 있다.
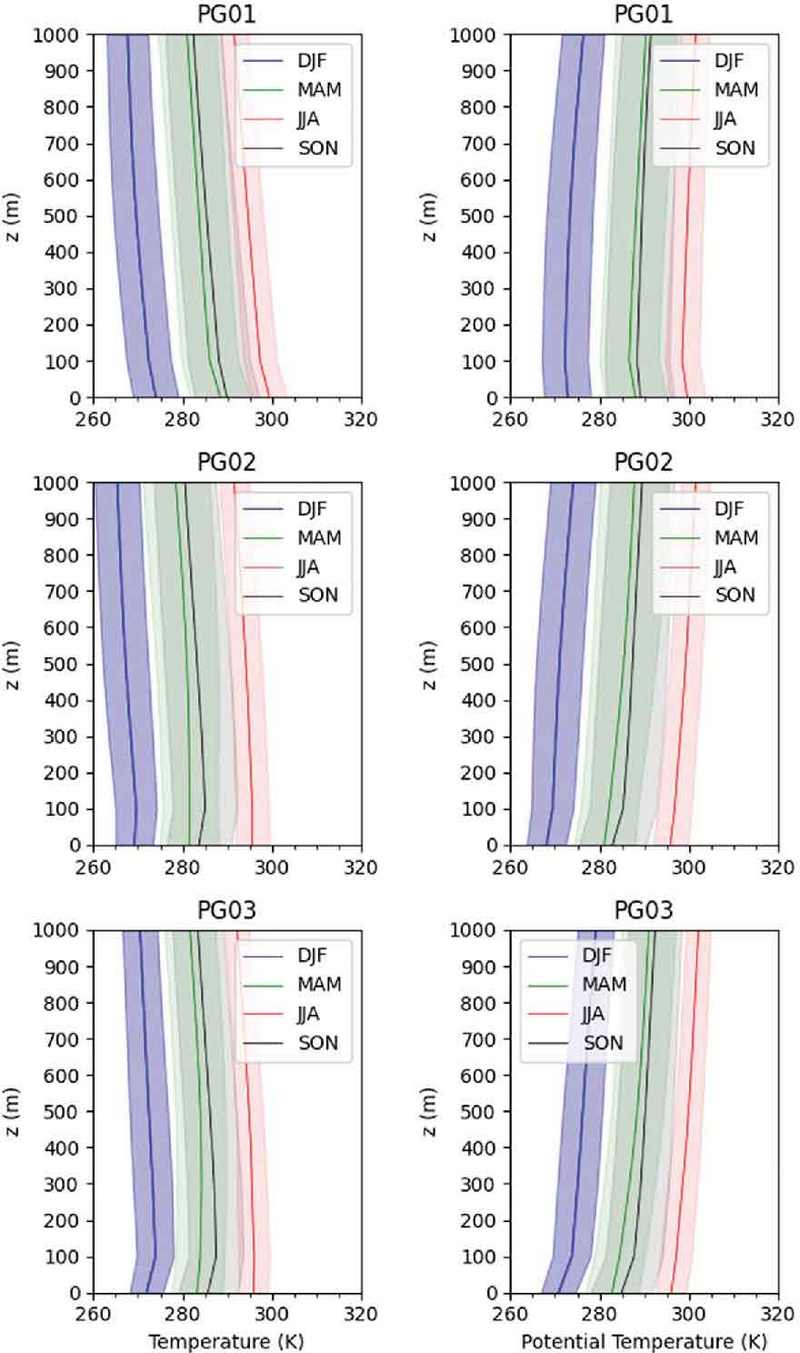
Vertical profiles of seasonal temperature and potential temperature according to atmospheric stability classes (PG). Each solid line represents the average of the overall profiles for each season.
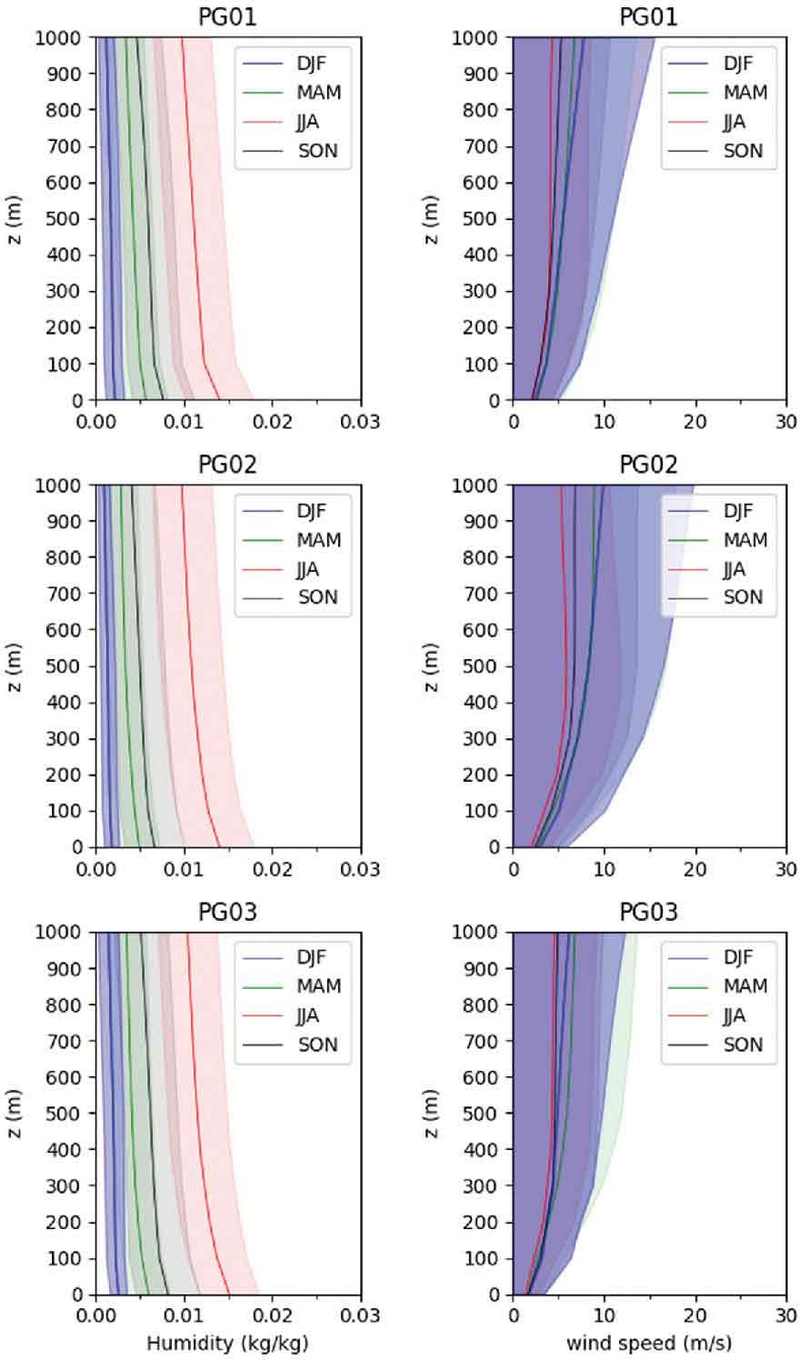
Figure 5는 대기안정도 등급에 따른 계절별 습도와 풍속의 연직 프로파일을 나타내었다. 전체적으로 습도는 고도가 높아질수록 감소하는 경향을 보인다. 습도 또한 온도(온위)와 유사하게 큰 계절적인 변화를 모든 대기안정도 등급에서 뚜렷하게 나타나고 있다. 여름에 대기 하층에서 약 0.015 kg kg-1 수준으로 가장 높은 습도가 나타나고 가을, 봄, 겨울 순서로 습도가 작아지는 특성을 보이며 불안정도가 높은 PG01 등급은 대기 하층에서 고도에 따른 습도의 연직 차이가 크게 나타난다. 이러한 특성은 일반적으로 풍속이 작고 일사량이 많은 경우 지표면 증발에 의한 대기 최하층 수증기 공급이 증가하여 발생할 수 있으며 대기의 상태를 불안정하게 만드는데 기여할 수 있다.
하층 풍속은 상대적으로 계절의 영향을 크게 받지 않는 요소로 다른 기상장에 비해 계절 변동성이 크지 않지만 상층으로 올라갈수록 봄과 겨울에 강하고 가을과 여름에 약한 계절적 변동성을 보인다.
3.2 입력자료를 활용한 대기확산모델링 예
특성에 맞게 분류한 기상장을 이용해 산출된 연직 프로파일 자료를 입력자료로 사용하여 대기확산 모델링을 실시하였다. 연구에 사용된 Woo et al. (2022) 입자 방출 시나리오는 대상 영역의 중심 부근인 세종대로 사거리에서 순간 방출을 가정하며, 라그랑지안 방출 입자수는 20,000이다.
본 연구에서 산출한 입력자료 중 겨울철 최대 빈도수를 나타내는 군집인 WD14WS03PG01의 사례 중하나인 2019년 2월 16일 17시에 대한 대기 확산 모의 예시가 Fig. 6에 나와있다. 해당 사례는 늦은 오 후 불안정 대류 경계층의 발달로 인해 풍향은 서북서(NWN) 방향으로 대기 경계층 내에서 대체로 균일하고 지상 부근의 풍속 시어가 강하게 나타나는 특징을 보인다(Fig. 6a). 건물의 영향으로 지표 부근의 복잡한 난류 흐름이 모의되고 있고 입자들은 주 풍향을 따라 주로 동남동(ESE) 방향으로 확산되나, 건물 등에 의한 난류의 영향으로 입자 방출 지점의 상류 확산과 도심 협곡을 따른 채널링 수송도 명시적으로 모의되었다(Figs. 6b, c). 기상장 군집 분류를 통해 획득한 프로파일 정보는 다양한 기상 조건을 반영할 수 있어 실제 도심 지역에서 기상장 변화에 따른 대기 분산 특성을 파악하는데 활용될 수 있을 것이다.
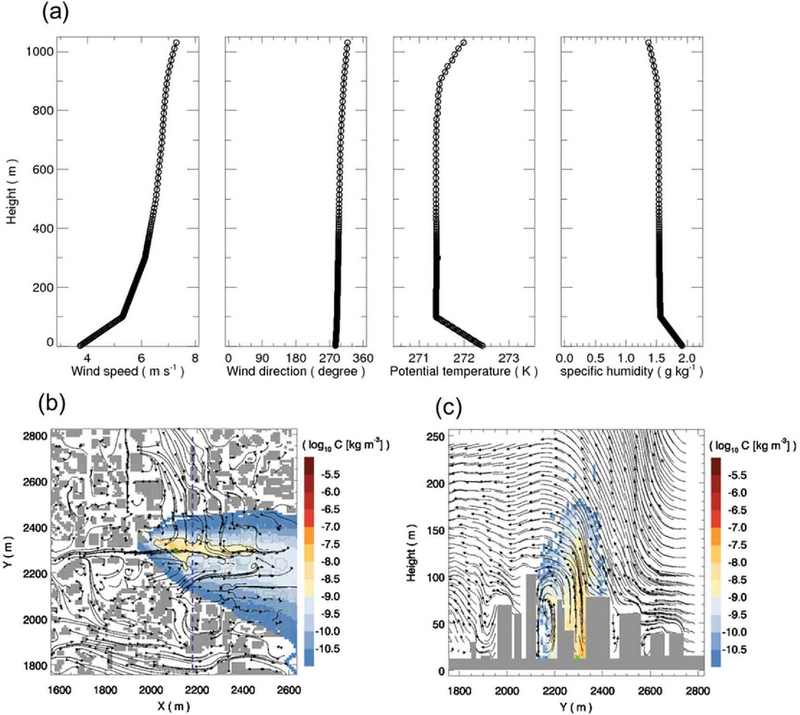
An example of atmospheric dispersion simulation for the most frequent cluster representative case in winter: (a) Vertical profile of meteorological fields from ERA5 input, (b and c) near-surface streamlines and particle concentration horizontal and vertical distributions. The streamline distribution represents a 10-min average, and the concentration distribution indicates the mean concentration between the surface and 300 m. The green mark represents the emission source location.
3.3 산출 기상장 적용 및 한계점
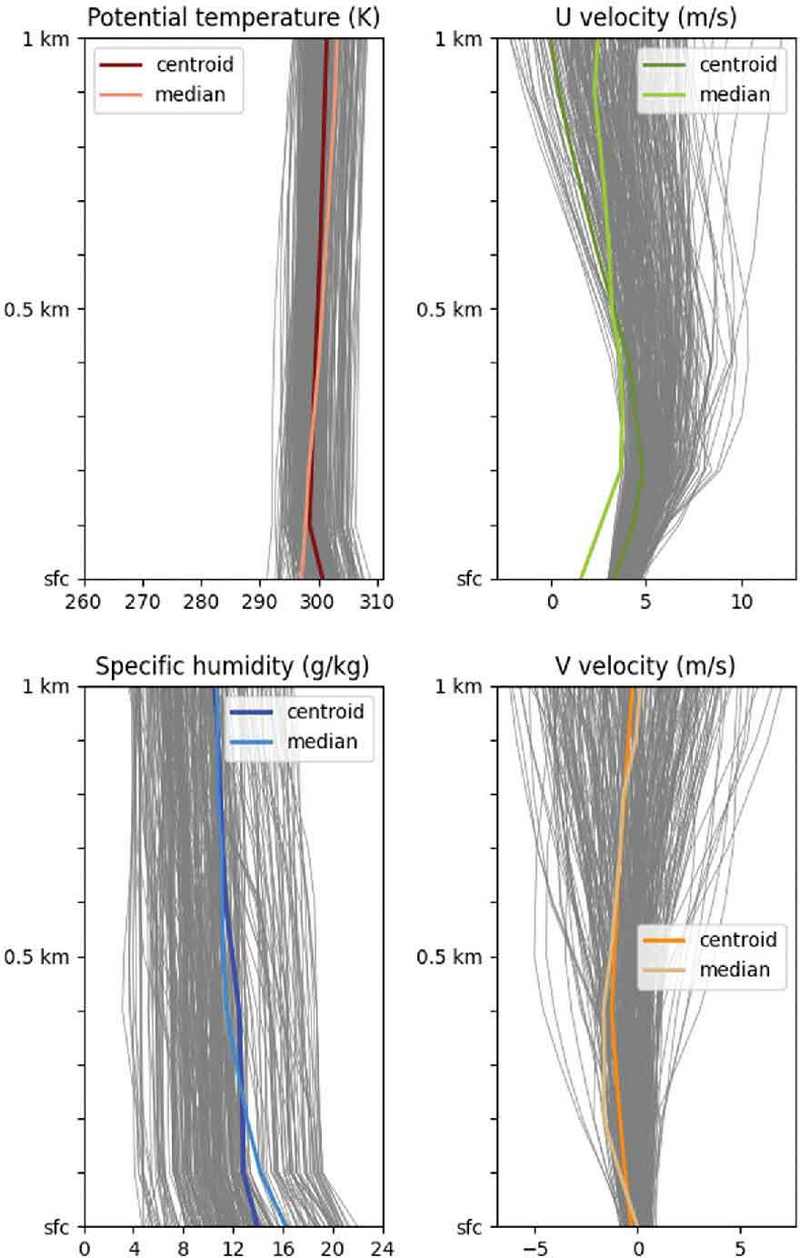
본 연구를 통해 192개 등급으로 특성에 맞게 분류된 기상장과 연직 프로파일은 대기확산 모델의 입력 자료로 사용될 수 있으며 보다 정확한 정보를 제공하여 향상된 결과를 도출할 수 있을 것이다. 각 기상장 분류별로 다수의 기상장 정보가 존재하는 경우, 보다 효율적인 대기확산 모델링을 위해 자기조직화지도(self-organizing map, SOM) 방법론 등에서 활용하는 대표 프로파일을 선정하여 활용할 수 있다. 예를 들어 Fig. 7과 같이 SOM으로 대표 프로파일(best matching unit; centroid 활용)을 선정하면 전체 프로파일을 비교적 잘 대표하는 프로파일 하나를 선정할 수 있고 이를 대기 확산 모델링에 사용하게 되면 전체 프로파일을 모두 모의하지 않아도 되어 효율적인 확산 모델 데이터베이스 구축이 가능하게 된다. 또한 이러한 군집 기법을 192 분류 등급에 적용하여 계절별 192개의 등급을 30개 내외의 차원으로 축소할 수도 있다. 그러나 과도한 차원 축소 과정은 확산 정보의 단편화로 이어질 수 있기 때문에, 차원 축소 과정이 대기확산 모델링 데이터베이스에 미치는 영향에 대해서는 더 깊이 있는 연구가 필요하다. SOM을 활용한 확산 데이터베이스 차원 축소에 대해서는 추가 연구가 진행 중에 있다.
4. 요약 및 정리
본 연구에서는 도시 규모의 오염물질 확산 모의를 위해 기상정보의 특성에 따라 기상장을 분류하고 각 분류에 따른 연직 프로파일을 산출하였다. ERA5의 지표 자료를 이용하여 풍향, 풍속과 대기안정도의 분 포를 분석 후 풍향 16단계, 풍속 4단계, 그리고 대기안정도는 3단계로 나누어 계절별로 총 192개의 등급으로 분류하였다. 대기안정도의 경우 지표의 일사량, 운량과 풍속을 이용해 P-G 방법을 이용하였다. 분류된 지표자료의 정보를 이용하여 지표 정보를 포함하는 하층 연직 프로파일을 산출하였다. 연직 프로파일에 대한 대기안정도는 리차드슨 수를 이용하여 구하고 지표의 P-G 대기안정도와 비교하여 불안정, 중립, 그리고 안정으로 각각 PG01, PG02, 그리고 PG03으로 이름 붙여 3등급으로 분류하였다. 두 자료의 대기안정도가 일치하는 경우만 사용하여 지표와 연직 프로파일의 상관성을 높여주었다.
지표 자료 특성을 이용한 192 등급 분류와 온도, 습도, 풍속과 온위의 연직 프로파일 분포를 확인했을 때 각각의 하층의 계절적 특성과 더불어 각 기상 변수의 특성 또한 연직 프로파일에도 잘 반영되는 것을 확인할 수 있었다. 대표적으로 온위의 경우 불안정 등급인 PG01에서는 고도에 따라 온위가 감소하고 안정 등급인 PG03에서는 고도에 따라 온위가 증가하는 모습을 볼 수 있었다.
Acknowledgments
본 연구는 원자력안전위원회의 재원으로 한국원자력안전재단의 지원을 받아 수행한 원자력안전연구사업의 연구결과입니다(No. 2105036).
REFERENCES
-
Arnold, D., C. Maurer, G. Wotawa, R. Draxler, K. Saito, and P. Seibert, 2015: Influence of the meteorological input on the atmospheric transport modelling with FLEXPART of radionuclides from the Fukushima Daiichi nuclear accident. J. Environ. Radioactivity, 139, 212-225.
[https://doi.org/10.1016/j.jenvrad.2014.02.013]

-
Bocquet, M., 2012: Parameter‐field estimation for atmospheric dispersion: application to the Chernobyl accident using 4D-Var. Quart. J. Roy. Meteor. Soc., 138, 664-681.
[https://doi.org/10.1002/qj.961]

-
Bowyer, T. W., R. Kephart, P. W. Eslinger, J. I. Friese, H. S. Miley, and P. R. J. Saey, 2013: Maximum reasonable radioxenon releases from medical isotope production facilities and their effect on monitoring nuclear explosions. J. Environ. Radioactivity, 115, 192-200.
[https://doi.org/10.1016/j.jenvrad.2012.07.018]

-
Chen, B., A. F. Stein, N. Castell, J. D. de la Rosa, A. M. Sanchez de la Campa, Y. Gonzalez-Castanedo, and R. R. Draxler, 2012: Modeling and surface observations of arsenic dispersion from a large Cu-smelter in southwestern Europe. Atmos. Environ., 49, 114-122.
[https://doi.org/10.1016/j.atmosenv.2011.12.014]

-
Cohen, M., and Coauthors, 2004: Modeling the atmospheric transport and deposition of mercury to the Great Lakes. Environ. Res., 95, 247-265.
[https://doi.org/10.1016/j.envres.2003.11.007]

-
Connan, O., K. Smith, C. Organo, L. Solier, D. Maro, and D. Hébert, 2013: Comparison of RIMPUFF, HYSPLIT, ADMS atmospheric dispersion model outputs, using emergency response procedures, with 85Kr measurements made in the vicinity of nuclear reprocessing plant. J. Environ. Radioactivity, 124, 266-277.
[https://doi.org/10.1016/j.jenvrad.2013.06.004]

-
Geng, X., Z. Xie, L. Zhang, M. Xu, and B. Jia, 2018: An inverse method to estimate emission rates based on nonlinear least-squares-based ensemble four-dimensional variational data assimilation with local air concentration measurements. J. Environ. Radioactivity, 183, 17-26.
[https://doi.org/10.1016/j.jenvrad.2017.12.004]

- Gifford, F. A., Jr., 1961: Use of routine observations for estimating atmospheric dispersion. Nucl. Saf., 2, 47-57.
-
Hersbach, H., and Coauthors, 2020: The ERA5 global reanalysis. Quart. J. Roy. Meteor. Soc., 146, 1999-2049.
[https://doi.org/10.1002/qj.3803]

-
Hwang, W. T., E. H. Kim, H. S. Jeong, H. J. Jeong, and M. H. Han, 2013: Influence of modelling approaches of diffusion coefficients on atmospheric dispersion factors. J. Radiat. Prot., 38, 60-67.
[https://doi.org/10.14407/jrp.2013.38.2.060]

-
Jeong, H., M. Park, H. Jeong, W. Hwang, E. Kim, and M. Han, 2013: Radiological risk assessment caused by RDD terrorism in an urban area. Appl. Radiation and Isotopes, 79, 1-4.
[https://doi.org/10.1016/j.apradiso.2013.04.018]

-
Jeong, S. J., 2021: A CFD study on odor dispersion around building array under different atmospheric stability conditions. J. Korean Soc. Atmos. Environ., 37, 1-16.
[https://doi.org/10.5572/KOSAE.2021.37.1.001]

- KEITI, 2014: The Current Status and Trends in the Application of Atmospheric Dispersion Models. Korea Environmental Industry and Technology Institute.
- Kim, C.-H., I.-S. Park, S.-J. Lee, J.-S. Kim, Y.-D. Hong, J.-S. Han, and H.-A. Jin, 2005: Evaluation of the effect of traffic control program on the ambient air quality in Seoul metropolitan area using the lower level stability index of atmosphere. J. Korean Soc. Atmos. Environ., 21, 243-257.
- Lee, J. H., D. H. Jo, and J. H. Cha, 2022: A study on the use of CFD for risk prediction of chemical terrorism in urban areas. J. Police Studies, 22, 59-77.
-
Lee, S. H., and K. H. Kwak, 2020: Assessing 3-D spatial extent of near-road air pollution around a signalized intersection using drone monitoring and WRF-CFD modeling. Int. J. Environ. Res. Public Health, 17, 6915.
[https://doi.org/10.3390/ijerph17186915]

-
Leelőssy, Á., F. Molnár, F. Izsák, Á. Havasi, I. Lagzi, and R. Mészáros, 2014: Dispersion modeling of air pollutants in the atmosphere: a review. Cent. Eur. J. Geosci., 6, 257-278.
[https://doi.org/10.2478/s13533-012-0188-6]

- MAMO, 2011: Metropolitan Air Quality Information. Metropolitan Air Quality Management Office.
-
Maronga, B., and Coauthors, 2020: Overview of the PALM model system 6.0. Geosci. Model Dev., 13, 1335-1372.
[https://doi.org/10.5194/gmd-13-1335-2020]

-
Mun, J., W. Jeon, and H. W. Lee, 2020: Impact of different meteorological initializations on WRF simulation during the KORUS-AQ campaign. J. Environ. Sci. Inter., 29, 33-44.
[https://doi.org/10.5322/JESI.2020.29.1.33]

-
Nakajima, K., T. Yamanaka, R. Ooka, H. Kikumoto, and H. Sugawara, 2020: Observational assessment of applicability of Pasquill stability class in urban areas for detection of neutrally stratified wind profiles. J. Wind Engineering and Industrial Aerodynamics, 206, 104337.
[https://doi.org/10.1016/j.jweia.2020.104337]

-
Oh, H.-S., S.-H. Lee, D.-W. Choi, and K.-H. Kwak, 2020: Comparison of the vertical PM2.5 distributions according to atmospheric stability using a drone during open burning events. J. Korean Soc. Atmos. Environ., 36, 108-118.
[https://doi.org/10.5572/KOSAE.2020.36.1.108]

-
Park, J., S.-Y. Lee, L.-Y. Choi, K. F. Daniel, and S.-W. Hong, 2023: Establishing and operating a test bench for assessment of pesticide drift by aerial application. J. Bio-Environ. Control, 32, 423-433.
[https://doi.org/10.12791/KSBEC.2023.32.4.423]

-
Park, M.-H., H.-D. Kim, and M.-Y. Kim, 2005: Sensitivity of air pollutants dispersion according to the selection of meteorological data -Case of Seongseo industrial complex of Daegu-. J. Environ. Sci., 14, 141-156.
[https://doi.org/10.5322/jes.2005.14.2.141]

- Pasquill, F., 1961: The estimation of the dispersion of windborne material. Meteor. Mag., 90, 33-49.
-
Povinec, P. P., and Coauthors, 2013: Dispersion of Fukushima radionuclides in the global atmosphere and the ocean. Appl. Radiation and Isotopes, 81, 383-392.
[https://doi.org/10.1016/j.apradiso.2013.03.058]

- RDA, 2010: Development of a CFD model to predict odor dispersion from livestock. Rural Development Administration.
- Seinfeld, J. H., and S. N. Pandis, 2006: Atmospheric Chemistry and Physics: From Air Pollution to Climate Change. 2nd Edition, John Wiley & Sons, New York.
-
Srinivas, C. V., R. Venkatesan, R. Baskaran, V. Rajagopal, and B. Venkatraman, 2012: Regional scale atmospheric dispersion simulation of accidental releases of radionuclides from Fukushima Dai-ichi reactor. Atmos. Environ., 61, 66-84.
[https://doi.org/10.1016/j.atmosenv.2012.06.082]

-
Stein, A. F., G. D. Rolph, R. R. Draxler, B. Stunder, and M. Ruminski, 2009: Verification of the NOAA smoke forecasting system: model sensitivity to the injection height. Wea. Forecasting, 24, 379-394.
[https://doi.org/10.1175/2008WAF2222166.1]

-
Stein, A. F., R. R. Draxler, G. D. Rolph, B. J. Stunder, M. D. Cohen, and F. Ngan, 2015: NOAA’s HYSPLIT atmospheric transport and dispersion modeling system. Bull. Amer. Meteor. Soc., 96, 2059-2077.
[https://doi.org/10.1175/BAMS-D-14-00110.1]

- Woo, J.-W., S.-B. Oh, S.-H. Park, and S.-H. Lee, 2022: Development of a detailed urban meteorological dispersion evaluation system. Proceedings of the 2022 Autumn Meeting of the Korean Association for Radiation Protection, 613-614.
-
Yang, H., G. Lee, M. Bae, and C. Yi, 2021: Estimation of the temperature reduction effect of heatwave response projects in urban spaces. J. Clim. Change Res., 12. 777-795.
[https://doi.org/10.15531/KSCCR.2021.12.6.777]

-
Yerramilli, A., and Coauthors, 2012: An integrated WRF/HYSPLIT modeling approach for the assessment of PM 2.5 source regions over the Mississippi Gulf Coast region. Air Qual, Atmos. Health, 5, 401-412.
[https://doi.org/10.1007/s11869-010-0132-1]