한국형수치예보모델 자료동화에서 위성 복사자료 관측오차 진단 및 영향 평가
Abstract
The observation error of satellite radiation data that assimilated into the Korean Integrated Model (KIM) was diagnosed by applying the Hollingsworth and Lönnberg and Desrozier techniques commonly used. The magnitude and correlation of the observation error, and the degree of contribution for the satellite radiance data were calculated. The observation errors of the similar device, such as Advanced Technology Microwave Sounder (ATMS) and Advanced Microwave Sounding Unit-A shows different characteristics. The model resolution accounts for only 1% of the observation error, and seasonal variation is not significant factor, either. The observation error used in the KIM is amplified by 3–8 times compared to the diagnosed value or standard deviation of first-guess departures. The new inflation value was calculated based on the correlation between channels and the ratio of background error and observation error. As a result of performing the model sensitivity evaluation by applying the newly inflated observation error of ATMS, the error of temperature and water vapor analysis field were decreased. And temperature and water vapor forecast field have been significantly improved, so the accuracy of precipitation prediction has also been increased by 1.7% on average in Asia especially.
Keywords:
Data assimilation, Observation error covariance, Advanced technology microwave sounder (ATMS), Desroziers technique, Hollingsworth and Lönnberg1. 서 론
모델 초기장의 정확도는 예측성능에 직접적인 영향을 미치므로 대기상태를 정확히 추정하는 것은 매우 중요하다. 그러나 특정 시간 실제 대기상태를 정확히 알 수 없으므로 단기 예측장에서 추정한 대기상태(모델 배경장)에 다양한 관측자료를 동화하여 최적의 모델 초기장을 생산한다. 자료동화과정에서 모델 배경장 대비 관측자료에 적정한 가중치를 할당하기 위해서 관측자료의 오차구조를 이해하고, 그 크기를 정확하게 진단하는 것이 중요하다. 모델에 동화되는 다양한 자료 중 위성 복사자료는 전구를 시·공간적으로 균일하게 관측할 뿐 아니라, 비교적 높은 정확도로 대기 상태 정보를 제공하므로 자료동화에서 중요도가 매우 높다. 위성 자료의 오차는 기기오차, 대표성 오차, 모델 오차, 전처리 오차 등 매우 다양한 원인에 의해 야기되는 것으로 알려져 있다. 기기 잡음에 의한 오차는 궤도상 측정을 통해 비교적 정확히 알 수 있지만, 그 외 오차의 크기를 각각 분리하는 것이 쉽지 않다. 단순화를 위한 몇몇 가정을 기반으로 관측오차 및 배경오차 공분산 연구가 진행되어 변분이나 칼만 필터 기반 동화시스템의 오차 공분산을 진단하여 사용하고 있다(Dee and Da Silva, 1999; Desroziers and Ivanov, 2001; Desroziers et al., 2005; Chapnik et al., 2006).
대부분의 현업 수치모델센터들은 자체 자료동화 체계에 최적화된 관측오차 산출 체계와 자료를 보유하고 있으며, 필요할 때 주기적으로 업데이트하고 있다. 현재 한국형수치예보모델(Korean Integrated Model; Hong and Coauthors, 2018) 자료동화에서 관측자료 오차정보는 다른 기관의 오차정보를 참고하거나, 동일한 관측오차를 여러 기기에 적용하기도 한다. 관측오차는 관측 품질뿐 아니라, 모델에 따라 최적의 값이 다르므로 주로 사용하는 관측오차 진단기법을 통해 KIM에 동화되는 관측자료의 오차 특성을 이해하고, 이를 반영하여 모델 초기장 향상을 위한 최적의 관측오차를 추정하려고 한다. 본 연구에서는 세계적으로 널리 활용되고 있는 Hollingsworth and Lönnberg (1986)와 Desroziers et al. (2005) 기법으로 KIM에 동화 중인 주요 위성 복사자료의 총 오차에서 관측오차를 진단하는 시스템을 구축하고, 마이크로파 위성자료인 ATMS (Advanced Technology Microwave Sounder)의 관측오차를 조정하였을 때 모델 분석장 및 예측성능에 미치는 영향을 분석하였다. 추후 모든 위성 복사자료의 오차 조정에 대한 연구의 기초를 마련하고자 한다.
2. 자 료
KIM에 동화되는 주요 위성 복사자료인 AMSU-A (Advanced Microwave Sounding Unit-A), ATMS, IASI (Infrared Atmospheric Sounding Interferometer), MHS (Microwave Humidity Sounder)의 관측오차를 진단하기 위해 필요한 정보는 관측된 밝기온도와 관측위치로 내삽한 모델장을 복사모델에 입력하여 추정한 밝기온도와 차이인 관측증분(First Guess departure, O-B) 및 분석장과의 차이인 분석잔차(Analysis departure, O-A)다.
통계정보 산출에 사용된 모델의 수평해상도는 약 25 km, 융합형4차원 앙상블 변분동화(Hybrid 4DEnVAR)를 이용하여 산출한 분석증분 해상도는 모델보다 낮은 약 50 km이다. 관측 자료는 관측 전처리과정인 KIM Package for Observation Processing (Kang et al., 2018)을 통해 편향보정과 솎아내기(thinning) 등 전처리과정을 통과하여 자료동화에 사용된 것이다. 편향보정은 2단계로 이루어지며, 위성과 지면 사이의 기하구조(geometry)에 의한 관측위치(scan angle)별 편향을 우선 제거하고, 매 분석시간 모델의 초기 추정값에서 산출한 대기층후(thinckness, 850~300 hPa, 200~50 hPa)를 이용하여 대기 물리량(airmass)에 따른 복사편향을 보정한다. 이후 자료동화 최소화 과정에서 대기층후 계수와 상수항을 조절하여 분석장에 최적화하는 변분 편향보정(Dee, 2004)을 수행한다. 관측자료의 공간상관을 제거하기 위한 솎아내기 간격은 위성에 따라 1o~3o 간격으로 수행된다.
본 연구에서는 관측오차의 계절특성을 파악하기 위해 2021년 1월과 7월 각각 15일 동안 관측증분 및 관측잔차 등의 정보를 추출하여 오차를 진단하였다. 진단된 관측오차는 계절에 따른 차이가 크지 않으므로 본 연구에서는 2021년 7월 15일간 분석된 결과를 제시하였다.
3. 관측오차 공분산 진단기법
자료동화는 모델에서 예측한 배경장과 관측정보를 결합하여 분석장을 생산하는 과정으로(Kalnay, 2003), 식(1)에 비용함수의 최소값을 찾는 것이다.
| (1) |
식(1)에서 x는 모델 상태벡터, xb는 이전 모델에서 예측한 배경장의 상태벡터, y는 관측벡터, B는 배경오차 공분산, R은 관측오차 공분산, H는 모델 배경장을 관측값으로 변환하는 관측연산자(observation operator)이다. 관측오차 공분산과 배경오차 공분산은 관측과 배경장의 오차특성에 대한 정보를 제공함으로써 각 항에 대한 가중치를 결정한다. 또한 비용함수의 2차 미분인 헤시안(Hessian)은 다음과 같다.
| (2) |
여기서 H는 관측연산자(H)의 자코비안(Jacobian)이다(Ide et al., 1997). 헤시안은 비용함수 최소화과정의 속도와 관계가 있어 적정하지 않은 관측오차 공분산은 변분과정의 수렴속도를 늦추거나 방해할 수도 있다(Haben et al., 2011). 즉, 관측오차 공분산은 관측자료의 가중치를 결정할 뿐 아니라, 최소화 과정의 속도에도 관여하고 있다.
관측오차 공분산은 주로 관측증분을 이용하여 산출한다. 관측오차와 배경오차가 서로 상관이 없고, 계통적인 오차(편향)는 없다고 가정하면 관측증분의 공분산은 모든 오차 즉, 관측기기의 잡음이나 관측과 모델의 해상도 차이나 복사모델의 불확실성에 의한 대표성 오차(representativeness error), 모델의 예측성능, 표면온도(Tsfc)와 같이 부정확하거나 불완전한 상태백터(χ)에서 기인한 오차를 포함한다(Andersson, 2004).
Hollingsworth and Lönnberg와 Desroziers 기법은 관측증분 공분산에서 관측오차와 배경오차를 분리하는 대표적인 진단 방법으로 이를 적용해 AMSU-A, MHS, ATMS, IASI의 관측오차를 진단하고, 위성 및 각 관측기기의 오차특성 분석하였다. ATMS 위성자료의 특성에 기반하여 관측오차를 증폭하고, 이를 모델에 동화하여 분석장 및 예측장에 미치는 민감도를 평가하였다.
3.1 Hollingsworth/Lönnberg 기법
Rutherford (1972)와 Hollingsworth/Lönnberg (이하 H/L) 기법은 배경오차는 공간적인 상관이 있지만 관측오차는 공간적으로 독립적이라는 가정에 기반하여 관측오차를 분리하였다. 예를 들어 두 관측지점(i, j)에서 관측증분의 공분산은 다음과 같다.
| (3) |
식(3)에서 E[ ]는 기댓값 연산자이고, (y–H(xb))i는 i지점의 관측증분이다. 관측증분 공분산은 관측오차와 배경오차의 상관을 무시하면 관측오차 공분산(Ri,j)과 관측공간상의 배경오차 공분산(HBHTi,j)의 합으로 나타낼 수 있다. 동일한 관측지점(i=j)에서는 관측증분 공분산은 배경오차 공분산과 관측오차 공분산의 합이다. 그러나 위치가 다른 관측점(i≠j)의 관측증분 공분산은 관측오차는 공간 상관이 없다는 가정에 의해 0이 되고, 배경오차 공분산에 의해 결정된다. 거리에 대한 관측증분 공분산으로 공분산/거리 상관식을 산출하여 두 관측점의 거리가 충분히 가까울 때(i≈j) 배경오차를 추정하고, 총 오차에서 이 값을 뺀 나머지, 즉 공간상관이 없는 부분을 관측오차로 한다. 이 기법은 라디오 존데의 관측증분으로 배경오차를 평가하기 위해 적용되었으며(Hollingsworth and Lönnberg, 1986), AIRS (Atmospheric Infrared Sounder) 복사량 자료의 오차와 채널 간 오차상관을 산출하는데 사용되었다(Garand et al., 2007).
H/L 기법을 적용하기 위해 위성자료의 관측증분을 거리에 따라 나누고, 관측거리에 대한 공분산을 산출하였다. 솎아내기 간격보다 가까운 관측자료들은 제거하고, 1,000 km 이내에 위치한 관측자료를 50 km 단위(IASI는 100 km)로 나누어 공분산을 계산하였다. Figure 1은 NOAA-20 (National Oceanic andd Atmospheric Administration) ATMS 자료 중 모델에 동화되는 채널에 H/L 기법을 적용하기 위해 채널별로 관측점 거리에 대한 공분산의 크기를 표시하였다. 거리에 따른 관측수는 Fig. 1 마지막 그림에 제시하였다. 공분산과 거리에 대한 상관식(파란 선)을 산출하고, 관측점 거리를 0으로 근사할 때 값을 배경오차에 의한 기여, 나머지는 관측오차 공분산으로 분리하였다. 관측자료의 거리가 가까워질수록 상관이 급격히 커지며, 거리가 멀어질수록 배경오차 공분산이 0으로 수렴하고 있어 배경과 관측의 편향은 잘 제거된 것으로 판단된다. 수증기 채널(ch18~22)의 공분산은 400 km까지 급격히 감소하고 이후 완만해지는 반면, 온도 채널은 거리에 따라 공분산 감소 기울기가 다소 완만하다. 특히 성층권 채널(ch14, 15)은 1,000 km 이상 거리에도 비교적 공분산이 크다. 이러한 성층권 자료의 특성은 Desrozier 기법으로 산출한 AMSU-A 자료에도 나타난다(Bormann et al. 2010). 두 관측의 관측증분 공분산은 거리가 가까워질수록 커지기 때문에 선형 함수로 외삽할 경우 공간상관이 과소 평가되어 관측오차는 과대 평가된다. 본 연구에서는 거리에 대한 3차 다항식(cov(r) = a0 + a1r + a2r2 + a3r3)을 적용하였으며, 이 함수는 다른 함수로 대체 가능하다.
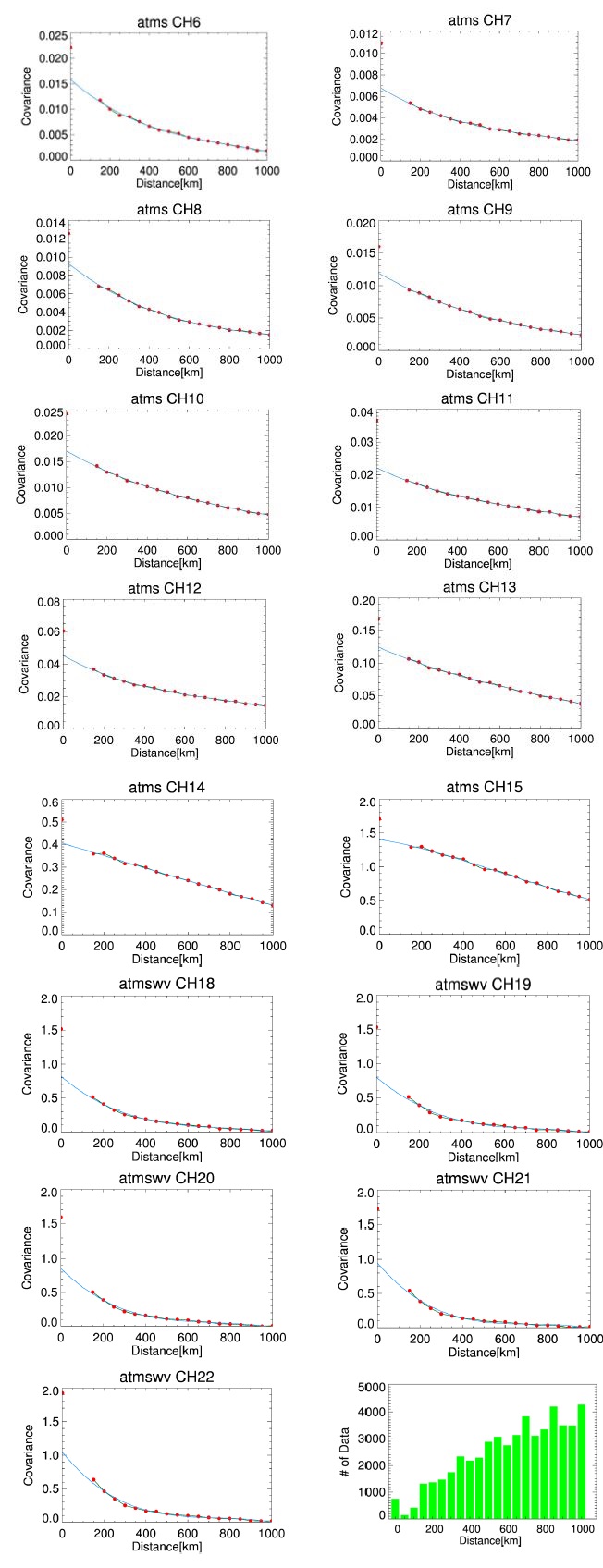
First-guess departure covariance (red dot) and its correlation (solid blue) for distance of NOAA-20 ATMS channels assimilated in KIM system. The numbers of collocations are shown in the last panel. Separation bins (50 km) with fewer numbers than those in center are not used. ATMS, Advanced Technology Microwave Sounder; KIM, Korean Integrated Model.
3.2 Desroziers 진단기법
변분동화과정이 관측과 배경장정보에 선형추정이론을 기반으로 분석장을 산출한다는 가정하에 관측증분과 관측잔차를 이용하면 관측공간에서 진단된 관측오차, 배경오차와 분석오차 정보를 유도할 수 있다. Desroziers et al. (2005)에서 유도한 관계식은 다음과 같이 요약할 수 있다.
| (4) |
| (5) |
R은 관측오차 공분산, HBHT는 관측점에서 산출된 배경오차 공분산, xa는 분석장의 상태 벡터이다. 이 기법에서 오차는 정규분포를 가지고 관측오차와 배경오차는 서로 독립적이라는 가정뿐 아니라, 분석장 생산에 사용한 오차정보가 실제 값을 정확히 반영한다는 가정에서 출발한다. Desroziers et al. (2005)은 정확하지 않은 관측오차를 적용하여 진단한 R의 대각항이 실제 값에 근사하는 것을 보였다. 본 연구에 사용한 자료동화시스템은 비교적 최적화되어 있는 상태라고 가정하고, 이 기법을 1회만 적용하여 오차를 진단하였다. 또한 편향보정을 실시한 관측자료를 사용하므로 배경장에 대한 편향은 제거되었다고 가정할 수 있으며, 분석장에 대한 편향은 공분산 산출 시 E [y – H(xa)] E [y – H(xb)] 항으로 제거하였다.
3.3 KIM 위성복사자료의 관측오차 진단
KIM에 동화되는 위성자료 중 연직 온도 및 수증기 정보를 제공하는 마이크로파 센서인 AMSU-A, MHS, ATMS와 적외파 센서인 IASI의 관측오차를 위성별로 진단하였다. 앞장에서 기술한 2개 기법으로 진단한 오차를 실제 모델에 사용하고 있는 관측오차 및 관측증분 표준편차와 비교하였다. 또한 채널별 오차 상관성, 전체 오차 대비 관측오차의 비율을 통해 각 관측자료의 기여도를 유추하고, 모델 해상도에 따른 관측오차를 비교하였다.
관측오차의 채널 간 상관관계을 알기 위해 오차 공분산을 다음과 같이 산출한다.
| (6) |
Ri,j는 i채널과 j채널의 오차 공분산을 의미한다. 채널 간 상관관계는 아래 식과 같이 오차 공분산을 대각항으로 나누어 산출할 수 있다. 이 값은 –1~1 값을 가지며, 두 채널 간 관측오차 상관의 크기를 나타낸다.
| (7) |
채널 간 상관이 큰 자료는 관측이 서로 독립적이라는 가정을 충족하지 않기 때문에 대각항만을 관측오차로 사용할 경우 그 크기를 증폭하여 동화할 필요가 있다.
각 관측자료의 기여도를 평가하기 위해 전체오차에서 진단된 관측오차나 배경오차가 차지하는 비율을 비교할 수 있는 지수를 산출하였다. 관측자료의 기여도를 k라고 하면 분석오차가 최소가 되는 최적의 기여도는 아래와 같다(Bouttier and Coutier, 1999).
| (8) |
관측품질이 낮아 관측오차가 매우 큰 경우(R ≫ HBHT) k는 0에 근사하고, 관측이 고품질인 경우에 k는 큰 값을 가진다. 관측과 배경정보의 정확도가 동일한 경우(R = HBHT) k는 0.5이므로 분석장은 관측과 배경장의 단순 평균 값이 된다. 그러나 관측자료의 기여도가 0.8 이상이면 비용함수의 수렴이 어려울 수도 있어 분석장 오차가 배경장 오차보다 커질 수도 있다.
모델 해상도에 따른 관측오차의 차이를 알아보기 위해 2개 해상도에 대해 관측오차를 진단하였다. 사용한 모델 해상도는 ne360과 ne180이며, 각각 12 km와 24 km의 격자크기를 가진다. 모델 해상에 의한 관측오차의 차이는 아래와 같이 비교하였다.
| (9) |
오차 비율이 음의 값이면 고해상도 모델의 관측오차가 작다는 것을 의미한다. 진단된 오차 및 관측증분 표준편차를 비교하여 모델 해상도에 따른 관측오차 차이를 산출하였다. 모델 해상도가 증가하면 대표성 오차가 줄어들 것이므로 관측오차 감소를 기대할 수 있다.
3.4 관측자료 특성 기반 관측오차 증폭
진단된 관측오차를 증폭하여 사용하는 것은 관측자료의 오차상관을 반영하기 위한 일반적인 방법이며, 부정확한 배경오차나 잔차(residual bias) 등에 의한 오차도 고려하기 위한 것이다. Bormann et al. (2016)은 IASI의 관측오차를 일괄적으로 1~4배 증폭하는 조정실험을 통해 채널 간 상관을 0으로 가정하면 관측오차를 2.5~3배 증폭할 때 가장 최선의 모델 성능이 나옴을 보였으며, 채널 간 상관을 고려할 경우에는 대각항의 오차를 1.75배 증폭하였을 때 모델 성능 개선이 큰 것을 보였다.
KIM 자료동화에서 관측오차 공분산은 채널 간 상관을 고려하지 않고 대각항만을 사용하며, ATMS 관측오차의 경우 대류권과 성층권채널에서 각기 다른 비율로 증폭하고 있다. 다른 모델링 센터에서도 관측오차 증폭에 대한 기준이 마련되어 있지 않고, 순차적으로 오차를 증폭하는 영향평가를 통해 증폭비율을 선정하여 적용하고 있다. 본 연구에서는 관측자료에 일률적인 증폭을 수행하기 보다는 채널에 따른 오차특성을 반영하여 물리적으로 설명할 수 있는 관측오차의 증폭(Inf)을 아래와 같이 고안하여 산출하였다.
| (10) |
첫 번째 항은 성층권 상층과 같이 모델의 정확도가 낮아 배경오차가 큰 영역에서 관측오차를 증폭하는 역할을 한다. 동화과정에서 배경오차는 조정하지 않고 관측오차만 크게 작아질 경우 동화과정 중 수렴에 방해가 될 수도 있기 때문에 이를 고려하기 위한 것이다. 두번째 항은 이웃 채널과 상관이 커서 관측자료의 독립성이 유지되지 않는 수증기 채널이나 하층 대류권 온도채널에서 관측오차를 증폭하여 상관에 의한 영향을 줄이는 역할을 한다. 새로 고안하여 계산한 채널 별 증폭값을 Desrozier기법으로 진단한 관측오차에 곱하여 새로운 관측오차를 산출하였다.
4. 결과 및 분석
4.1 관측오차 진단
Figure 2는 주요 위성 복사자료(ATMS, AMSU-A, MHS, IASI)에 대해 모델에 사용되는 관측오차(회색 점선)와 관측증분의 표준편차(빨간 실선), H/L 기법 관측오차(파란 실선), Desrozier 기법으로 진단된 관측오차(보라색 실선)의 크기를 채널별로 나타낸 것이다. 각 관측오차의 크기를 비교해 보면 H/L 관측오차나 Desroziers 관측오차는 관측증분의 표준편차보다 작으며, 모델에 사용하는 관측오차는 진단된 값에 비해 증폭되어 있다. 예를 들어 IASI의 경우 진단된 관측오차에 비해 대략 2~3배, MHS와 ATMS 수증기채널(atmswv)에서 5배 정도, AMSU-A나 ATMS는 채널에 따라 3~8배 증폭된 값을 관측오차로 사용되고 있다. 채널별 차이를 보기 위해 Table 1에 ATMS 자료에 사용 중인 실제 관측오차(εKIM)와 진단된 관측오차의 크기를 위성별로 비교하였다. ATMS 관측오차는 관측증분 표준편차에 비해 2.3~6.8배, Desroziers 관측오차에 비해 2.7~8.7배 큰 값이며, 채널별로 크기가 매우 다르다. 예를 들어 대류권채널(ch6~11)에서 사용 중인 관측오차는 Desroziers 관측오차에 비해 3배 정도인 반면, 성층권채널(ch12~15)에서는 6배 가량 큰 값으로 증폭되었다. 성층권 채널에서 관측오차를 크게 증폭한 것은 해당영역의 모델 정확도가 낮아 배경오차가 큰 것을 반영한 것으로 유추된다.

The profiles of observation errors for ATMS, AMSU-A, MHS, and IASI channels assimilated in KIM system. Dotted gray, solid blue, and solid purple lines indicate the observation error useded in KIM assimilation system, the Hollingsworth/Lönnberg error, and the Desroziers diagnostic error, respectively. Also shown are the standard deviation of FG departure (solid red).
Figure 3은 Desroziers 기법으로 진단된 채널 간 오차 공분산에서 식(7)을 이용하여 산출한 ATMS와 AMSU-A, MHS 자료의 채널별 관측오차 상관관계를 나타낸 것이다. ATMS는 AMSU-A와 유사한 파장 영역을 관측하지만 상대적으로 넓은 관측폭을 가지며, 대류권 온도채널 1개와 수증기채널 2개가 추가된 형태로 인해 AMSU-A에 비해 채널 간 상관이 크다(Bormann et al., 2013)고 알려져 있으며, 본 연구에서 산출한 관측오차의 채널 간 상관관계도 AMSU-A에 비해 큰 것을 확인할 수 있다. 다소 과장된 가정에서 출발한 산출기법에 의해 채널 간 비대칭을 보이지만, 본 연구에서는 채널 간 상관 정도를 분석하기 위한 자료로 사용하므로 그대로 제시하였다. ATMS 자료의 이웃 채널과 상관은 대류권 채널(ch6~9)에서 0.5로 성층권채널(ch12~15)의 0.2에 비해 크며, 수증기채널은 최대 0.9까지 커지는 채널도 확인되었다. AMSU-A는 ATMS에 비해 대류권 채널의 상관이 거의 없는 것을 알 수 있다. 이러한 차이는 온도채널뿐 아니라, 수증기채널에서도 뚜렷하게 나타나서 MHS 채널 간 상관은 약 0.6 정도로 ATMS 수증기채널(atmswv)에 비해 낮은 상관을 보인다. 이러한 특성은 ATMS에만 있는 저 잡음 처리기(low noise amplifier)에 의해 채널 간 상관관계가 증폭되었기 때문이다(Bormann et al., 2013; Kim et al., 2014). 또한 대류권 하층 온도채널이나 수증기채널의 상관은 모델과 관측의 해상도가 일치하지 않아 생기는 대표성 오차 또는 부정확한 구름탐지로 오염된 관측에 의한 영향으로 더욱 커진다(Eresmaa, 2014; Weston et al., 2014). 진단된 오차보다 관측오차를 크게 증폭하는 이유는 이러한 기기의 채널 간 상관성을 반영하기 위한 것이다. 최근 많은 연구에서 단순하게 관측오차 공분산의 대각항을 증폭하는 것보다 관측오차의 상관을 반영할 때 관측자료의 정보를 모델에 충분히 동화할 수 있음을 보였다(Weston et al., 2014, Bormann et al., 2016). 다른 수치모델링 센터에서는 각 관측자료의 관측오차 공분산의 구조를 고려한 동화를 실시하고 있으나, 현재 KIM은 관측자료의 채널 간 오차 상관을 0으로 하고 증폭한 관측오차의 대각항을 사용하고 있다. 또한 AMSU-A와 ATMS는 각각 관측자료의 오차특성이 다르지만 동일한 관측오차를 적용하고 있어 이에 대한 고려가 필요하다.
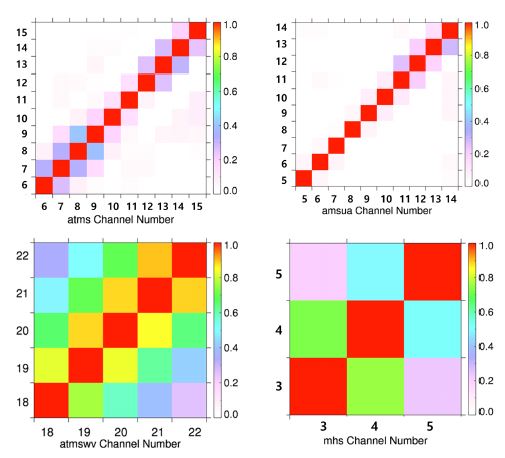
Estimation of inter-channel correlations for NOAA-20 ATMS and MetOp-C AMSU-A and MHS based on the Desroziers diagnostics.
Figure 4는 주요 위성 복사자료(ATMS, AMSU-A, MHS, IASI)에서 진단된 관측오차 및 배경오차를 이용하여 식(8)로 계산한 관측 기여도(k)를 비교한 것이다. H/L 기법으로 진단한 관측자료의 기여도는 k_H/L (회색 선), Desroziers 기법으로 진단된 관측자료 기여도는 k_Des (빨간 선)로 표기하였다. ATMS 자료의 k_Des는 0.3~0.5 이내의 값을 가지며, 신규 위성인 NOAA20 위성자료의 기여도가 Suomi-NPP (National Polar-orbiting Partnership) 자료보다 높게 진단된다. 수증기채널(ch18~22)의 기여도는 위성에 따른 차이는 없으며, 상층 수증기채널(ch21~22)의 기여가 하층 채널에 비해 크다. 반면 ATMS 관측자료의 k_H/L은 k_Des에 비해 큰 값을 가지며 온도채널에서 0.5 이상이고, 성층권에서는 거의 1에 근사하는 0.8~0.9의 값을 가진다. 반면 수증기 채널에서는 관측 기여도가 0.4 가량이며 k_Des와 크게 다르지 않다. 온도채널에서 k_H/L이 k_Des에 비해 큰 것은 해당 채널의 기여도가 큰 것을 의미하기 보다는 과대 진단된 배경오차 때문이며, 이는 배경오차 산출에 사용되는 거리 상관함수의 오류나 관측자료의 공간상관이 0이라는 과장된 가정에서 기인한 것으로 판단된다. 따라서 H/L 기법은 성층권 채널 관측오차 진단에 적절하지 않다. 신규 위성인 MetOp-C AMSU-A의 k_Des가 대류권 채널에서 NOAA20이나 NPP 위성의 ATMS 값에 비해 작으므로 단일 위성 비교시에 ATMS의 관측기여도가 더 큰 것으로 판단된다. IASI는 다른 두 관측종에 비해 관측기여도가 낮으며, 특히 성층권채널(ch 1~61)에서 k_Des는 0.1 값을 가진다. 반면 수증기채널의 기여도는 0.6 이상의 값이다. 추후 채널에 따라 기여도가 크게 다른 원인을 면밀하게 분석할 필요가 있다.
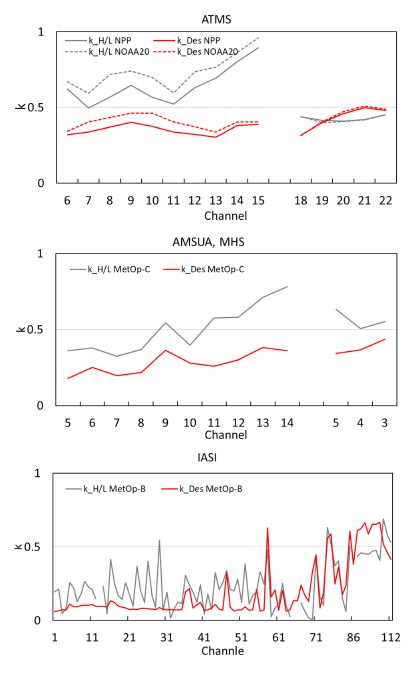
Estimation of the optimal weight k the ratio between background error covariance and total error covariance for NPP and NOAA-20 ATMS (top), AMSU-A, MHS (middle), and IASI (bottom) data based on the H/L (k_H/L, solid gray) and Desroziers diagnostics (k_Des, solid red) in KIM system.
해상도가 다른 두 모델에 대해 진단된 NOAA-20 ATMS의 관측증분 표준편차, H/L 관측오차, Desrozier 관측오차의 차이를 Fig. 5는 나타냈다. 실제 모델 해상도가 높으면 전체 오차를 의미하는 관측증분의 표준편차가 모든 채널에서 감소한 것을 알 수 있다. ATMS 최상층 채널인 15번 채널은 모델 해상도 증가에 따라 모든 오차가 감소하여 대략 4%의 비율이 모델 해상도에 따른 오차로 진단된다. 최상층을 제외한 다른 채널에서는 Desrozier 기법으로 산출한 관측오차는 1%가량 감소하였다. 모델 해상도에 따른 관측오차의 차이가 유의미하게 큰 값은 아니므로 저해상도 모델 기반으로 산출한 오차를 고해상도 모델에서 사용 가능할 것으로 판단된다.

The normalized observation error difference for NOAA-20 ATMS between different model resolutions (ne360 vs ne180). The normalized observation error difference calculated by the equation(Rne360-Rne180Rne360×100)
Figure 6은 현재 KIM 자료동화에 사용하고 있는 관측오차(Obserr_KIM)와 진단된 관측오차를 증폭하여 비교한 것이다. 대류권 채널에서 각 관측오차가 Obserr_KIM과 유사한 크기가 갖고, Bormann et al. (2016)이 제안한 증폭비율을 고려하여 H/L 관측오차는 4배(Obserr_HL×4), Desrozier 오차는 3배(Obserr_Des×3)를 모든 채널에 동일하게 증폭하였다. 식(10)을 이용하여 계산한 증폭비율을 각 채널에 적용하여 새로운 관측오차(Obserr_Des×Inf)를 산출하였다. 새로 산출한 증폭크기는 온도채널에서는 2.5~3가량이며, 수증기 채널에서는 3.5가량으로 결정되었다. Figure 6에서 ATMS 자료의 채널 특성을 반영한 Obserr_Des×Inf는 다른 오차에 비해 성층권채널에서 증폭비율이 가장 크고, 채널 간 상관이 큰 수증기 채널(atmswv)의 오차는 Obserr_Des×3에 비해 다소 큰 3.5 K이다.
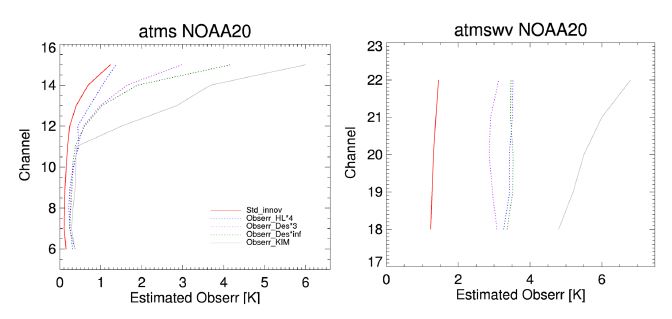
The profiles of inflated observation error for NOAA-20 ATMS channels used in KIM system. The observation error assumed in KIM assimilation system (solid gray), the Hollingsworth/Lönnberg error multiplied by 4 (dotted blue), the Desroziers diagnostic error multiplied by 3 (dotted purple), and weighted by considering inter-channel correlation and BG error (dotted green). Also shown are the standard deviation of FG departure (solid red).
관측오차 증폭크기를 결정하기 위해 각 관측오차를 동화에 사용하여 자료동화시 수렴 소요시간 및 비용함수 값을 비교하였다. Obserr_Des×3는 비용함수 수렴에 걸리는 반복 횟수가 1회 증가하고 비용함수 감소비율(초기 비용함수와 최종 비용함수의 비)이 수증기 채널에서 다른 오차에 비해 큰 반면, 두 오차(Obserr_Des×Inf, Obserr_HL×4)는 수렴속도와 비용함수 감소비율이 유사하였다. 각 관측오차를 적용하여 산출한 분석장을 유럽 중기예보 센터의 통합 예보 시스템(Integrated Forecasting System, IFS) 분석장과 비교한 결과, 전 고도에서 고르게 오차가 개선된 Obserr_Des×Inf를 모델 영향평가를 위한 최종 관측오차로 선정하였다.
4.2 모델 예측성능에 미치는 영향
관측오차 조정에 따른 모델 민감도 평가를 위해 규준모델(CTL)과 실험모델(EXP)을 구성하였다. 규준모델은 비정역학 육면체구(cubed-sphere) 격자체계에 ne180 (~24 km) 해상도의 모델(KIM3.6a)이고, 자료동화는 앙상블 모델 오차를 동화에 적용한 하이브리드 4차원 앙상블 변분(Hybrid-4DEnVar) 과정을 이용한다(Kwon et al., 2018). ATMS 자료의 관측오차 조정에 따른 영향을 분석하기 위해 CTL과 EXP의 관측종을 종관관측(SONDE, SURFACE, AIRCRAFT)과 위성관측 2종[GPSRO (Global Positioning System. Global Navigation Satellite System Radio Occultation), ATMS]로 제한하였다. CTL의 ATMS는 기존 관측오차를 사용하고, EXP의 ATMS 관측오차는 4.1절에서 선정한 값으로 조정하였다. ATMS 관측오차 조정이 모델 결과에 미치는 영향을 살펴보기 위해 2021년 7월 1~21일까지 순환실험을 실시하였고, 예측장 검증은 7월 6~21일까지 16일간 수행하였다.
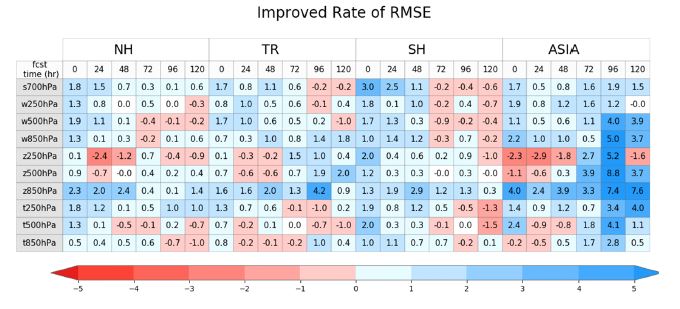
Figure 7은 CTL대비 EXP 분석장의 온도와 비습 오차 개선율(improvement rate) 분포로 European Center for Medium-Range Weather Forecast/Integrated Forecast System 분석장을 기준으로 두 실험의 분석장 오차(root mean square error) 차이를 정규화([RMSE (CTL)–RMSE (EXP) / RMSE (CTL)] × 100)한 것이다. 개선율이 양수이면 EXP가 CTL보다 IFS 분석장에 가까운 값을 의미한다. (a)와 (b)는 순환실험 첫 번째 분석장의 오차 개선율을 위도평균한 분포이다. 첫 번째 분석장은 동일한 초기장에 대해 CTL과 EXP의 분석증분 차이를 뚜렷하게 볼 수 있다. EXP 온도장은 극 지역 일부를 제외한 대부분 위도대에서 오차가 감소하고, 주로 500 hPa 이상 고도에서 영향이 나타나며, 전구 평균 약 1.25% 개선되었다. 온도에 비해 크기는 작지만 수증기장도 CTL에 비해 모든 위도대에서 고르게 오차가 감소하였다. 첫 분석장에서 오차가 감소한 영역은 관측오차를 작게 조정한 채널의 영향 고도와 일치하여 관측오차 조정이 분석장을 개선하는 방향으로 작용하는 것을 알 수 있다. 반면, 관측오차 조정이 작았던 대류권 하층 온도장에는 분석장의 변화가 크지 않다. Figures 7c, d는 온도와 비습 분석장의 오차 개선율 시계열이다. 실험기간 내내 온도 분석장 오차 감소를 유지하며, 성층권 특히 1~10 hPa에서 가장 큰 개선을 보이고 개선율은 8% 내외이다. 해당고도의 오차 감소가 점차 확대되어 15일부터 대류권 하층을 포함한 전체 고도로 확대되었다. 기간평균 온도장 오차 개선율은 1.68%이다. 수증기장 역시 실험기간 동안 오차 감소가 유지되며, 특히 300~700 hPa 고도에서 개선이 크다. 수증기장도 시간에 따라 오차 개선이 점점 커진다. 관측오차 조정에 의한 수증기장 오차를 보기 위해 Fig. 8에 IFS 분석장 대비 CTL 비습 편차(a)과 EXP와 CTL 증분(b) 및 오차 차이(c)의 기간 평균분포를 제시하였다. Figure 8a에 의하면 CTL 수증기장은 IFS 분석장에 비해 적도 부근에 0.5 g/kg 과습이 있고, 고위도는 다소 건조하다. Figure 8b에서 EXP의 수증기 증분은 CTL의 과습 영역을 건조하게, 북위 60도 이상의 건조 영역은 보다 습윤하도록 수증기증분을 더하여 전구에 걸쳐 CTL 수증기장 편차 및 오차를 줄이는 역할을 한다. 즉, 관측오차 조정으로 관측자료가 자료동화를 통해 적정하게 반영될 경우 모델의 초기장이 보다 개선됨을 알 수 있다.

Zonal means of the normalized difference of root mean squared error (improvement rate, IR) of (a) temperature and (b) specific humidity at first analysis filed, and timeseries of the normalized difference of root mean squared error of (c) temperature and (d) specific humidity between the control (CTL) and experiment (EXP). Positive (blue) values means an of EXP improvement compared to CTL. The CTL and EXP have been verified against IFS analysis field.
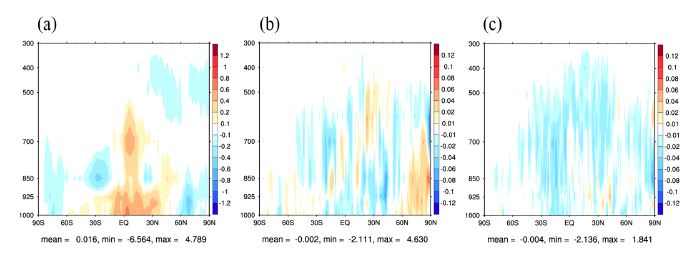
Zonal mean of specific humidity (a) bias of CTL against IFS analysis field, (b) increments difference, and (c) root mean square error difference between EXP and CTL during the period from 1 to 21 July 2021.
관측오차 조정으로 모델 초기장의 온도와 수증기장 오차 감소를 확인하였고, 예측장에 미치는 영향을 분석하기 위해 2021년 7월 6일부터 21일까지 IFS 분석장 대비 주요 지역/변수/고도/예측시간에 대해 예측장을 검증하여 EXP의 예측장 오차 개선율을 계산하였다. 예측장 비교 결과는 Fig. 9에 제시하였다. 검증영역은 북반구(NH), 적도(TR), 남반구(SH), 아시아(ASIA)이고, 검증인자는 비습(s), 바람(w), 지위고도(z), 온도(t)이다. 검증고도는 상층(250 hPa), 중층(500 hPa), 중 하층(700 hPa), 하층(850 hPa)이고, 초기장을 포함해 24시간 간격으로 120시간 예측장까지 검증하였다. EXP가 CTL에 비해 오차가 감소한 영역을 파란색으로 표시하였다. 검증 기간 동안 EXP는 CTL에 비해 전구에서 초기장 오차가 감소하였다. 북반구는 주요 인자에서 평균 1% 이상 개선되었고, 관측자료가 많은 남반구는 1.6%가량 개선되었다. 온도장의 경우, 하층보다 상층 대류권인 250 hPa 고도에서 2배가량 개선이 되는 것으로 나타났다. 아시아의 경우 250 hPa 온도장은 예측장 전체 기간에 오차가 감소하여 5일 예측장은 4.0% 개선된 반면, 대류권 하층은 예측 초반에 약 0.2% 성능이 저하되나, 2일 이후 예측성능은 개선되는 것으로 나타났다. 3~5일 예측장에서 지위고도나 온도장 개선은 평균 3.4%로 북반구 영역 평균에 비해 높다. 아시아영역은 주로 대륙으로 구성되어 있어 해상 자료만 사용하는 ATMS의 영향이 비교적 약하고, 관측오차가 주로 대류권 상층 및 성층권에서 조정되어 대류권 중하층에 미치는 영향이 크지 않았기 때문으로 판단된다. 700 hPa 습도장은 초기장뿐 아니라, 북반구 및 아시아영역에서는 전 예측시간에서 개선을 보이고 있다. 적도 및 남반구에서는 예측초반에는 오차가 감소하지만, 3일 이후부터는 0.2%~0.6%가량 다소 증가하였다. 관측자료가 많은 적도 및 남반구 영역은 관측오차 조정으로 수증기 관측의 영향이 커져서 초기장은 크게 개선되지만, 예측장 후반까지 개선이 유지되지 않는 것을 알 수 있다.
5. 요약 및 결론
본 연구에서는 KIM에 동화하는 주요 위성복사자료의 관측오차를 여러 기관에서 공통적으로 사용하는 H/L 기법과 Desrozier 기법을 적용하여 진단하는 체계를 구축하고, 이를 기반으로 각 관측자료의 관측오차 크기 및 상관관계, 관측자료의 기여도 등을 분석하였다. 같은 기기라도 위성에 따라 관측오차의 특성이 달라지는 것을 알 수 있었다. 반면 계절에 따른 차이는 크지 않으며, 모델의 해상도에 따른 오차의 차이도 1%가량이므로 크게 영향을 주지 않는 것으로 판단된다. KIM에 사용 중인 관측오차는 진단된 오차에 비해 채널에 따라 3~8배가량 큰 값이 사용되고 있다. 이 값은 타 기관에 비해 매우 큰 값이며, 특히 ATMS나 AMSU-A 성층권 채널에서 크게 증폭된 값을 사용하고 있다. 본 연구에서 채널 간 상관과 배경오차와 관측오차의 비를 기준으로 관측자료의 특성이 반영된 관측오차의 증폭크기를 산출하였다. 새로 산출한 ATMS 관측오차를 적용한 민감도 평가 수행 결과, 모델 초기장의 온도 및 수증기장의 오차가 감소하였고, 예측장의 정확도도 증가하였다. 아시아 영역에서 예측장이 뚜렷하게 개선되었고 제시하지 않았지만, 강수 예측 정확도가 5일 예측 평균 1.7% 개선을 보였다. 향후 다른 위성자료에 대해서도 관측자료의 특성을 고려해 관측오차를 최적화함으로써 모델 예측 성능을 개선할 수 있을 것으로 판단된다.
마이크로파 연직탐지기인 AMSU-A와 ATMS는 위성 및 기기에 따라 관측오차의 크기나 구조가 다르지만, KIM은 기기의 차이와 상관없이 동일한 관측오차를 사용하고 있어 개선이 시급하다. 또한 IASI의 경우, 성층권 관측자료의 기여도 0.1 이하로 다른 위성에 비해 4배가량 낮은 것으로 평가되었으며, 이는 관측오차 조정뿐 아니라, 편향보정 등의 개선을 통해 관측자료의 영향을 증대하기 위한 다양한 시도가 필요하겠다. 진단된 관측자료의 오차특성을 반영하는 연구는 관측자료의 영향을 증대하고, 초기장과 예측장 성능 개선에 긍정적인 영향을 미칠 것으로 기대된다.
Acknowledgments
본 논문의 개선을 위해 좋은 의견을 제시해 주신 심사위원께 감사를 드립니다. 본 연구는 기상청 출연사업인 (재)차세대수치예보모델개발사업단의 4차원 고품질 기상분석을 위한 최신 자료동화기술 개발(KMA2020-02211)의 지원을 받아 수행되었습니다.
References
- Andersson, E., 2004: Modelling the temporal evolution of innovation statistics. In: Proceedings of Seminar on Recent Developments in Data Asimilation for Atmosphere and Ocean, 8-12 September 2003. ECMWF.
-
Bormann, N., A. Collard, and P. Bauer, 2010: Estimates of spatial and inter-channel observation error characteristics for current sounder radiances for NWP, part I: Methods and application to ATOVS data. Q. J. R. Meteorol. Soc., 136, 1036-1050.
[https://doi.org/10.1002/qj.616]

-
Bormann, N., A. Fouilloux, and W. Bell, 2013: Evaluation and assimilation of ATMS data in the ECMWF system. J. Geophys. Res. Atmos., 118, 12970-12980.
[https://doi.org/10.1002/2013JD020325]

-
Bormann, N., M. Bonavita, R. Dragani, R. Eresmaa, M. Matricardi, and A. McNally, 2016: Enhancing the impact of IASI observations through an updated observation-error covariance matrix. Q. J. R. Meteorol. Soc., 142, 1767-1780.
[https://doi.org/10.1002/qj.2774]

- Bouttier, F., and P. Coutier, 1999: Data Assimilation Concept and Methods. European Centre for Medium-Range Weather Forecasts, 59 pp.
-
Chapnik, B., G. Desroziers, F. Rabier, and O. Talagrand, 2006: Diagnosis and tuning of observational error in a quasi-operational data assimilation setting. Q. J. R. Meteorol. Soc., 132, 543-565.
[https://doi.org/10.1256/qj.04.102]

-
Dee, D. P., 2005: Bias and data assimilation. Q. J. R. Meteorol. Soc., 131, 3323-3343.
[https://doi.org/10.1256/qj.05.137]

-
Dee, D. P., and A. M. da Silva, 1999: Maximum-likelihood estimation of forecast and observation error covariance parameters. Part I, Methodology. Mon. Weather Rev., 127, 1822-1834.
[https://doi.org/10.1175/1520-0493(1999)127<1822:MLEOFA>2.0.CO;2]

-
Desroziers, G., and S. Ivanov, 2001: Diagnosis and adaptive tuning of information error parameters in a variational assimilation. Q. J. R. Meteorol. Soc., 127, 1433-1452.
[https://doi.org/10.1002/qj.49712757417]

-
Desroziers, G., L. Berre, B. Chapnik, and P. Poli, 2005: Diagnosis of observation background and analysis-error statistics in observation space. Q. J. R. Meteorol. Soc., 131, 3385-3396.
[https://doi.org/10.1256/qj.05.108]

-
Eresmaa, R. 2014: Imager-assisted cloud detection for assimilation of infrared atmospheric sounding interferometer radiances. Q. J. R. Meteorol. Soc., 140, 2342-2352.
[https://doi.org/10.1002/qj.2304]

-
Garand, L., S. Heilliette, and M. Buehner, 2007: Interchannel error correlation associated with AIRS radiance observations: Inference and impact in data assimilation. J. Appl. Meteorol. Climatol., 46, 714-725.
[https://doi.org/10.1175/JAM2496.1]

-
Haben, S. A., A. S. Lawless, and N. K. Nichols, 2011: Conditioning of incremental variational data assimilation, with application to the Met Office system. Tellus A, Dyn. Meterol. Oceanogr., 63, 782-792.
[https://doi.org/10.1111/j.1600-0870.2011.00527.x]

-
Hollingsworth, A., and P. Lönnberg, 1986: The statistical structure of short-range forecast errors as determined from radiosonde data. Part I: The wind field. Tellus, Ser A, Dyn Meterol Oceanogr., 38A, 111-136.
[https://doi.org/10.1111/j.1600-0870.1986.tb00460.x]

-
Hong, S.-Y., and Coauthors, 2018: The Korean Integrated Model (KIM) system for global weather forecasting. Asia-Pac. J. Atmos. Sci., 54, 267-292.
[https://doi.org/10.1007/s13143-018-0028-9]

-
Kalnay, E., 2003: Atmospheric Modeling, Data Assimilation and Predictability. Cambridge University Press, 341 pp.
[https://doi.org/10.1017/CBO9780511802270]

-
Kang, J.-H., and Coauthors, 2018: Development of an observation processing package for data assimilation in KIAPS. Asia-Pac. J. Atmos. Sci., 54, 303-318.
[https://doi.org/10.1007/s13143-018-0030-2]

-
Kim, E., C.-H. J. Lyu, K. Anderson, R. V. Leslie, and W. J. Blackwell, 2014: S-NPP ATMS instrument prelaunch and on-orbit performance evaluation. J. Geophys. Res. Atmos., 119, 5653-5670.
[https://doi.org/10.1002/2013JD020483]

-
Kwon, I.-H., and Coauthors, 2018: Development of an operational hybrid data assimilation system at KIAPS. Asia-Pac. J. Atmos. Sci., 54, 319-335.
[https://doi.org/10.1007/s13143-018-0029-8]

-
Rutherford, I. D., 1972: Data assimilation by statistical interpolation of forecast error fields. J. Atmos. Sci., 29, 809-815.
[https://doi.org/10.1175/1520-0469(1972)029<0809:DABSIO>2.0.CO;2]

-
Weston, P. P., W. Bell, and J. R. Eyre, 2014: Accounting for error in the assimilation of high-resolution sounder data. Q. J. R. Meteorol. Soc., 140, 2420-2429.
[https://doi.org/10.1002/qj.2306]