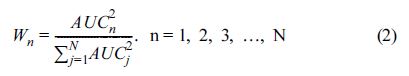Development of the Seasonal Korean Aviation Turbulence Guidance (KTG) System Using the Regional Unified Model of the Korea Meteorological Administration (KMA)
Sources of aviation turbulence vary through the seasons, especially in the East Asia including Korean peninsula, associated primarily with the changes in the jet/front system and convective activities. For this reason, a seasonal Korean aviation Turbulence Guidance (KTG) system (seasonal-KTG) is developed in the present study by using pilot reports (PIREPs) and analysis data of the operational Unified Model (UM) of the Korea Meteorological Administration (KMA) for two years between June 2011 and May 2013. Twenty best diagnostics of aviation turbulence in each season are selected by the method of probability of detection (POD) using the PIREPs and UM data. After calculating a weighting value of each selected diagnostics using their area under curve (AUC), the 20 best diagnostics are combined with the weighting scores into a single ensemble-averaged index by season. Compared with the current operational-KTG system that is based on the diagnostics applying all seasons, the performances of the seasonal-KTG system are better in all seasons, except in fall.
Keywords:
Pilot report (PIREP), seasonal Korean aviation Turbulence Guidance (KTG) system (seasonal-KTG), Unified Model (UM)1. 서 론
항공 난류는 대기 중에서 항공기에 직접적으로 영향을 끼치는 약 10~1,000 m 크기의 난류로 정의되며(Lester, 1994), 일반적으로 10,000~25,000 ft (FL100-250; 약 3.3~7.6 km 상공)의 고도에서 발생한 난류는 중층 난류, 25,000 ft (FL250) 이상에서 발생한 난류는 상층 난류로 분류된다. 이러한 항공 난류는 구름이 없거나 층운형 구름이 존재하는 맑은 하늘에서 발생하는 청천 난류(Clear-Air Turbulence; CAT) (Ellrod et al., 2003)가 대부분을 차지하고 있다. 미국의 국가운수안전위원회(National Transportation Safety Board)의 연차보고서에서 CAT가 날씨와 관련한 항공 사고의 주요 원인임이 기록된 바 있으며(NTSB, 2009), 한국항공철도안전조사위원회(Aviation and Railway Accident Investigation Board; ARAIB)의 통계 조사에서도 1957년 이래로 날씨와 관련된 한국 항공기 사고의 가장 큰 발생원인(약 24%)이 난류임을 밝힌 바 있다(Kim and Chun, 2011b).
한국은 국토의 약 70%가 산악 지역으로 이루어져 있으므로, 풍상측의 대기 안정도나 산악으로 유입되는 하층 바람에 따라 다양한 형태의 산악파가 나타나게 되며, 이것이 한국에서 발생하는 난류의 주요 원인 중 하나이다(Kim and Chun, 2011a; Kim and Chun, 2012). 또한 한국을 포함한 동아시아 지역은 전 세계에서 가장 강한 제트류가 존재하는 곳으로, 관성 불안정, 시어 불안정 등에 의한 난류 발생 확률이 높은 곳이다(Jaeger and Sprenger, 2007; Koch et al., 2006; Min et al., 2011). 한국 및 동아시아에서의 항공 산업이 발전하고, 항공 운행량이 급격하게 증가함에 따라, 순항 고도에서 예기치 못하게 발생하여 피해를 주는 항공 난류에 대한 정확한 예보의 필요성이 최근 더욱 커지고 있다.
현재 기상청에서 제공되고 있는 현업 수치예보모델의 수평 해상도가 약 12 km로, 수평 해상도가 많이 높아졌으나 수평규모가 10~1,000 m 정도인 항공난류를 수치예보모델에서 명시적으로 예측하는 것은 아직 불가능하다(Kim et al., 2011). 그러나, 수치예보모델 격자에서 계산되는 중규모 대기 운동으로부터 난류 규모의 운동으로 에너지가 캐스케이드 된다는 가정(Cho and Lindborg, 2001; Dutton and Panofsky, 1970)을 적용시킨다면, 중규모 운동을 현실적으로 예측할 수 있는 현업 수치예보모델을 통한 난류 발생의 예측이 가능하게 된다(Kim et al., 2011; Kim and Chun, 2011b). Sharman et al. (2006)은 미국에서 관측된 pilot report (PIREP)와 현업수치예보모델 자료를 사용하여, 이전 연구들을 통해 개발된 여러 난류진단지수들을 계산한 뒤, 그들의 예측성에 따라 달리 가중치를 적용시켜 하나의 난류예측지수로 통합하는 Graphic Turbulence Guidance (GTG) 시스템을 개발하였으며, 이렇게 통합된 GTG 단일지수의 난류 예측성이 개별난류진단지수들의 그것보다 훨씬 뛰어나다는 것을 보였다. Kim et al. (2009)은 기상청의 30 km 수평 격자간격 MM5 (5th generation Mesoscale Model; Grell et al., 1994) 기반의 지역예보모델(Regional Data Assimilation and Prediction System; RDAPS)과 한반도에서 관측된 각 난류 강도별[null (NIL), light (LGT), moderate (MOD), severe (SEV), extreme (EXT)] PIREP 자료를 GTG 방법론에 적용시켜 2003년부터 2008년까지 관측된 항공 난류의 예측에도 단일지수들보다 GTG 통합지수의 예측성이 좋다는 것을 밝혔다. 최근 Kim and Chun (2011b, 2012)은 12 km 수평 해상도를 갖는 기상청 통합모델(Unified Model; UM) 기반의 RDAPS를 이용하여 GTG 방법론을 기반으로 한 한국형 항공난류 예측(Korean Aviation Turbulence Guidance; KTG)시스템을 개발하였고, KTG는 현재 항공기상청에서 현업화되고 있다.
Figure 1은 2012년 9월 1일 12 UTC에 FL320-360사이에서 평균된 현업-KTG의 난류 예측 지역과 이시간대를 중심으로 ± 2시간 이내에 발생한 난류들을 각 난류 강도별 부호를 사용해 비교한 그림이다. 현업-KTG는 중국 하얼빈부터 몽골을 지나는 큰 지역에 걸쳐서 중강도 이상의 난류(moderate or greater; MOG)가 발생할 것이라고 예측하였고, 실제 발생한 MOG 지점과 대부분 잘 일치하는 것을 알 수 있다. 러시아 지역과 한국의 남쪽 해상, 일본의 동남쪽 해상에서 발생한 NIL에 대해서도 현업-KTG가 잘 예측하였음을 알 수 있다.

Locations of the turbulence observations over East Asia occurred within 2 h of 1200UTC on 1 September 2012 superimposed on the turbulence forecasting by the operational- KTG system at z = 32000~36000 ft. The thresholds of NIL-, LGT-, and MOG-levels are 0, 0.3, 0.475, respectively. The observed NIL, LGT, and MOG-level events are depicted as conventional symbols of turbulence intensity ( , , and ), respectively.
난류를 발생시키는 주요 원인들은 계절에 따라 다르게 나타난다. 겨울철에는 한국 및 동아시아 지역에 나타나는 강한 제트류와 상층 전선이 난류를 일으키는 주요 원인이 되며, 여름철과 봄철에는 몬순, 태풍과 같은 대류 시스템이 난류 발생에 영향을 끼친다(Kim et al., 2009; Kim and Chun, 2011a). 현업-KTG시스템의 경우, 구성요소들을 구축하는 데 있어서 계절의 구분 없이 1년간(2011.06~2012.05)의 PIREP과 RDAPS 분석장을 이용하였기 때문에 위에서 언급한 계절에 따른 난류의 특성을 고려할 수 없었다. 본 연구에서는 계절별로 발생하는 난류를 가장 잘 나타내는 진단변수들을 선택하고 그것들을 결합하여 계절마다 달리 적용되는 계절-KTG 시스템을 만들고자 하였다. 본 논문의 구성은 다음과 같다. 2장에서는 계절-KTG 시스템의 방법론 및 검증에 대해 설명할 것이며, 3장에서는 계절-KTG와 현업-KTG의 각 계절에 따른 난류 예측 결과를 비교 분석할 것이다. 마지막으로 4장에서는 결론 및 요약을 제시할 것이다.
2. 계절-KTG 시스템
계절-KTG 시스템의 기본적인 방법론은 현재 항공 기상청에서 현업으로 사용되는 KTG(Kim and Chun, 2012)와 유사하며, 가장 큰 차이점은 계절마다 서로 다른 난류진단지수를 선택하여 KTG 시스템을 구축한다는 것이다. 계절-KTG 시스템 구축방법을 간략하게 설명하면 다음과 같다. 첫번째 단계는 각 계절마다 적용될 20개의 난류진단지수들에 대한 look-up table을 만드는 단계로, look-up table에는 20개의 난류진단 지수들의 예측성을 대표하는 area under curve (AUC)값과 그것들의 각 난류 강도(NIL, LGT, MOD, SEV, EXT)별 임계값들이 포함된다. 기존 연구들을 통해 개발되었던 총 74개의 개별 난류진단지수들을 기상청 RDAPS 자료를 이용하여 계산한 뒤, 동아시아 지역에서 관측된 PIREP의 위치 및 시간(± 2시간 이내)과 가장 가까운 격자점에서 계산된 난류진단지수들의 값들을 관측된 난류 강도별로 구분하여 누적시킨다. 이렇게 각 난류 강도별로 누적된 개별 난류진단지수 값들의 평균값은 그 지수들의 난류 강도들(NIL-MOD)에 대한 임계값(T1-T3)으로 결정되며, SEV와 EXT의 경우 관측된 난류의 개수가 작아 평균값을 결정하기 어렵기 때문에, 개별 난류진단지수별로 누적된 전체 값들 중 98%, 99%에 해당하는 값들을 SEV와 EXT에 대응하는 임계값(T4, T5)으로 결정한다.
다음으로 POD (probability of detection; Mason, 1982) 방법을 통해 PIREP에 기록된 NIL과 MOG 난류들에 대한 각 난류진단지수들의 예측성을 검증한다. 이 방법은 MOG 난류가 관측된 지점과 가장 가까운 모델 격자점에서 계산된 난류지수값이 주어진 임계값보다 클 확률인 POD “yes” (PODY)와 NIL 관측 지점 근처의 격자점에서 계산된 난류지수값이 주어진 임계값보다 작을 확률인 POD “no” (PODN)을 구하여 예측성을 고려한다. 이 때 임계값은 누적된 지수값들의 최소값과 최대값 사이에서 임의로 일정하게 변화시켜가며 주어진다. 이렇게 주어진 임계값들에 따라 계산된 PODN과 PODY의 값들을 x-y도면에 나타내어 연결한 뒤, 그 커브 아래의 넓이인 AUC를 각 개별 난류진단지수의 난류 예측성으로 간주한다. 그 후 각 개별 난류진단지수들의 AUC를 비교하여, 예측성이 좋은 상위 20개의 개별 난류 진단지수들을 선별해 look-up table을 구성한다. Table 1은 2011년 6월부터 2012년 5월까지 1년 동안 RDAPS의 분석시간(0000, 0600, 1200, 1800 UTC)을 중심으로 ± 2시간 이내에 관측된 MOG와 NIL의 사례에 대해 예측성이 좋았던(AUC값이 큰) 상위 20개의 개별 난류진단지수들을 나열한 look-up table로, 항공기상청의 현업 KTG에 사용되고 있는 look-up table과 같다. 참고로 한반도 내에서 관측된 PIREP 자료는 항공기상청에서, 동아시아 지역에서 관측된 PIREP 자료는 미국 국립기상연구소의 Sharman 박사로부터 제공받았다. Table 1의 결과를 보면 전선, 연직시어 등 주요 난류진단지수를 Richardson number로 나눈 개별 난류진단지수들이 NIL 및 MOG 예측에 가장 크게 기여하는 예측성 상위 10개의 지수들 중 8개에 해당하는 것으로 나타났다. Table 1에 보인 난류진단지수들의 수식은 Kim et al. (2009)과 Jang et al. (2009)에 상세히 설명되어 있다.

Thresholds (T1, T2, T3, T4, and T5) corresponding to null, light, moderate, severe, and extreme intensities of upperlevel turbulence and AUC values for best 20 diagnostics for calculating the combined KTG index that are based on the 1-yr (2011.06~2013.05) PIREP data over East Asia and Unified Model (UM) based on operational Regional Data Assimilation and Prediction System (RDAPS) in the Korea Meteorological Administration (KMA). Formulations of all indices can be found from Jang et al. (2009) and Kim et al. (2009).
본 연구에서는 2011년 6월부터 2013년 5월까지 2년간의 RDAPS와 동아시아 지역 내 발생한 PIREP 자료를 각 계절에 해당하는 기간으로 나누어 위에서 설명한 현업-KTG와 같은 방법을 통해 계절별 look-up table을 구성하였다. 각 계절마다 발생되는 난류의 주요 원인들이 다르기 때문에, 선택된 20개의 난류진단 지수들의 종류와 예측성은 각 계절마다 다르게 나타난다. 2년 자료를 이용해 만들 수 있는 계절-KTG는 모두 12개로, 각 해마다 네 계절-KTG가 구성되어 8개와 두 해의 계절 자료를 이용한 4개가 합해져서 모두 12개가 된다. Table 2는 2011/12 December-January-February (DJF) look-up table로, 그 중 하나인 2011/12년 겨울철(2011.12~2012.02)의 예측성 상위 20개의 개별 난류진단지수들과 각각의 난류강도별 임계값, 그리고 AUC값을 나타낸 것이다. 현업-KTG와 비교했을때(Table 1), 상위 10개의 개별 난류진단지수들 중 7개가 일치함을 알 수 있다.

The same as in Table 1, except for the best 20 indices of 2011/12 DJF KTG that is based on the 3-month PIREP data over East Asia and KMA-RDAPS analysis from December 2011 to February 2012.
두 번째 단계는 선행 단계에서 구축된 계절별 KTG구성요소들을 현업 통합모델에 적용하는 것으로, 이하의 과정은 현업-KTG와 같다. 계절-KTG의 난류진단지수들을 현업 통합모델의 모든 격자점에서 계산한다. 계산된 개별 난류진단지수들의 수학적 크기와 단위가 각기 다르기 때문에, 개별 난류진단지수별로 난류 강도(NIL, LGT, MOD, SEV, EXT)들에 대응된 임계값들(T1, T2, T3, T4, T5)을 각각 0, 0.25, 0.5, 0.75, 1에 1 : 1로 대응시킨 후, 0에서 1사이의 값들로 표준화 시킨다. 이렇게 표준화된 개별 난류진단지수 값(D*n)들은 (1)식을 통해 각 지수들의 예측성에 따라 가 중치를 달리 적용시켜 하나의 난류예측인자(KTG)로 통합된다.
위 (1)식에서의 i, j, k는 UM 자료의 격자점 위치를, N은 KTG로 통합할 때 사용된 개별 난류진단지수의 개수를 의미하며, 본 연구에서의 N은 20개이다. 참고로 (1)식에서 사용되는 각 지수들의 가중치(Wn)는 (2)식에 의해 계산된다.
Figure 2는 초기 1년(2011.12~2012.11)간의 PIREP과 RDAPS로 구성된 계절-KTG 시스템을 이용하여 계산한 같은 계절 내 임의의 시각에서의 KTG 예보장과 그 시간대에서 2시간 이내에 관측된 PIREP을 비교한 것으로, 네 계절-KTG 모두 해당 날짜에 발생한 난류들을 잘 예측함을 알 수 있었다. 특히, 봄철에 난류 예측성이 좋은 상위 20개의 난류진단지수를 통합하여 계산한 March-April-May (MAM)-KTG (Fig. 2b)의 경우, 해당 날짜에 대해 예측한 KTG의 난류 강도별 위치와 관측된 NIL, LGT, MOD의 위치가 정확히 일치하는 것을 확인할 수 있었다. 또한 LGT 이상 강도의 난류들이 북서태평양, 특히 일본의 동쪽 해양 영역에서 발생한 다른 계절들과 달리, 가을철에는 중국 및 몽골 영역에서 LGT 이상 강도의 난류들이 발생한 것을 알 수 있었다.

The same as in Fig. 1, except at (a) 2012.12.18 1200 UTC, (b) 2013.04.07 1200 UTC, (c) 2012.06.03 1200 UTC, and (d) 2012.09.01 1200 UTC using the seasonal-KTG system constructed by the PIREPs and RDAPS data in 2011/2012 (December 2011~November 2012). The meanings of , , and are same as Fig. 1.
마지막 단계는 계절-KTG의 예측성을 검증하는 과정으로, POD방법을 이용하여, 최근 2년간(2011.06~2013.05) 0000, 0600, 1200, 1800 UTC를 중심으로 2시간 이내에 한국과 동아시아 지역에서 관측된 PIREP에 대한 검증을 수행하였다. 본 연구에서 고려한 2년 기간에 관측된 PIREP의 개수를 상층과 중층으로 나누어 살펴보았을 때, 상층에서는 총 20,480개 중 NIL이 13,702개, MOG가 1,009개 관측되었으며, 중층에서는 총 625개 중 NIL이 439개, MOG가 39개 관측되었다. 특히, 계절-KTG를 계산하는 데 사용되는 계절별 PIREP의 경우, 중층의 자료가 현저히 적어 중층 계절-KTG에 대한 예측성을 검증할 수 없었다. 따라서 본 연구에서는 상층 PIREP만을 사용하여 상층 계절-KTG만 개발하여 예측성을 검증하였다.
3. 계절-KTG 검증
본 연구에서는 2년(2011.06~2013.05) 간의 UMRDAPS자료와 상층 PIREP을 계절별로 나누어 분류한 뒤, 앞의 2에서 설명한 방법론을 적용하여 각 계절에 적합한 상층 계절-KTG 구성요소들을 결정하였다. 모두 12개의 계절-KTG가 구성되었으며, 아래에 보일 계절-KTG의 검증은 계절-KTG를 구성한 자료보다 과거 해의 계절에 대해서는 이루어지지 않았다. 예를 들어, 2012-June-July-August (JJA)-KTG system으로 2011-JJA의 관측자료를 검증하지는 않았다.
Figures 3과 4는 각각 초기 1년(2011.06~2012.05: 이하 P1)과 최근 1년(2012.06~2013.05: 이하 P2)의 계절별 관측 난류에 대한 계절-KTG와 현업-KTG system의 예측성을 보인 것이다. P1 기간에는 겨울철을 제외하고는 현업-KTG의 예측성이 계절-KTG의 예측성 보다 높았다. 그러나 봄철에는 계절-KTG와 현업-KTG 모두 AUC값이 0.8 이상으로, 다른 계절에서보다 높은 예측성을 보였다. AUC 값이 0.8 이상이 된다는 것은 KTG가 실효성 있는 난류예측정보로 제공될 수 있다는 것을 의미한다(Fahey, 1993; Sharman et al., 2006). 또한 네 계절 모두 P12 (2011.06~2013.05) 기간의 자료를 통해 구축된 계절-KTG보다 P1 기간의 자료를 통해 구축된 계절-KTG가 상대적으로 높은 예측성을 보였다. P2 기간에는(Fig. 4) 겨울과 봄철에는 계절-KTG가 현업-KTG보다 예측성이 높았으며, 여름에도 2011-12 JJA-KTG를 제외하고는 계절-KTG가 현업-KTG보다 예측성이 높았다. JJA를 제외하고는 계절-KTG와 현업-KTG가 모두 0.8 이상의 AUC를 나타내어 그 정확도가 높았다. 여름철에 KTG의 예측성이 다른 계절에 비해 낮은 것은 이전 연구에서도 잘 나타난 것으로(Kim et al., 2009; Kim et al., 2011), 그 주된 이유는 현재까지 개발된 난류진단지수들이 여름철 청천난류를 잘 나타내지 못하기 때문이다. 각 계절에서 가장 예측성이 높았던 계절-KTG를 현업-KTG와 비교한 결과, 가을철을 제외한 나머지 세 계절에서 계절-KTG가 현업-KTG보다 예측성이 높게 나타남을 확인하였다. 계절-KTG와 현업-KTG의 P1과 P2 기간 동안의 계절별 난류 예측성 비교는 Table 3에 정리하였다.

PODY and PODN performance statistics of each year’s seasonal-KTG and two-years seasonal-KTG systems along with the operational-KTG system in (a) 2011 JJA, (b) 2011 SON, (c) 2011/2012 DJF, and (d) 2012 MAM.

Seasonal forecast evaluation of the operational- and seasonal-KTG systems during the past two years (2011.06~2013.05). JJA, SON, DJF, and MAM denote June-July-August, September-October-November, December-January- February, and March-April-May, respectively.
상층 PIREP의 계절별, 연별 분포를 나타내는 Table 4를 통하여 계절-KTG 검증에 사용한 MOG PIREP의 개수를 살펴보면, P1 기간보다 P2 기간의 모든 계절에서 MOG의 개수가 많은 것을 확인할 수 있다. NIL의 경우는 가을철과 겨울철에만 P2 기간일 때 빈도수 보다 높게 나타났다. PIERP의 개수가 KTG의 예측성에 미치는 영향을 확인하기 위해서는 향후 좀 더 긴 기간의 PIREP을 사용해야 할 것이다.
4. 요약 및 결론
본 연구노트에서는 계절별 난류 발생 요인을 고려하여 난류를 예측할 수 있는 계절 한국형 항공난류예측시스템(계절-KTG)의 방법론을 제시하고, 최근 2년간의 난류 예측성을 조사하였다. 기상청 RDAPS과 PIREP을 이용하여 계절마다 달리 적용되는 계절별 상위 20개의 개별 난류진단지수들과 그것들의 임계값, AUC들을 결정한 뒤, 앙상블 평균하여 하나의 통합난류예측지수를 계산하였다. 이전 연구들에 의하면, KTG 구성요소들을 결정하는 데 있어 사용되는 PIREP의 기간이 길수록, 또는 현업 통합모델의 해상도가 높아지거나, 모델이 상층 대기운동을 잘 예측할수록 KTG의 난류 예측성이 좋아짐을 증명한 바 있다(Kim and Chun, 2011b, 2012). 본 연구에서 사용된 PIREP은 2011년 6월부터 2013년 5월까지 2년 자료로, 계절별로 나누어 사용해야 하는 점을 감안했을 때, 중층 PIREP의 개수가 현저하게 작아, 본 연구에서는 통계적으로 의미가 있는 상층 계절-KTG만 개발하였다. 차후 더 긴 기간의 PIREP이 축적되면, 중층 계절-KTG도 구축할 수 있을 것이다.
구축된 계절-KTG를 최근 2년간의 관측된 항공난류 사례에 대해서 예측성을 검증하고, 현업-KTG의 예측성과 비교하였다. P1 (2011.06~2012.05)에는 겨울철을 제외하고는 현업-KTG의 예측성이 더 좋았으나, P2(2012.06~2013.05) 기간에는 가을철을 제외하고, 계절-KTG가 현업-KTG보다 예측성이 좋았다. 또한 2년 자료를 사용하여 구축된 계절-KTG보다 1년 자료를 사용하여 구축된 계절-KTG가 P1과 P2 기간에 모두 높은 예측성을 보였다. 특히 P2 기간 자료를 사용하여 구축된 네 계절-KTG은 모두 예측성이 0.8 이상의 값을 보였다. 이와 같은 결과는 기상청 RDAPS의 상층장 예측성이 P2 기간에 다소 향상(personal communication)되어, 전반적으로 P2 기간의 난류 예측성이 현업-KTG와 계절-KTG 모두에서 높았던 것으로 보인다. 향후 더 긴 기간의 자료가 확보된다면, 현재의 현업-KTG 시스템과 계절-KTG 시스템을 보다 발전시켜 한국 및 동아시아 지역의 난류 특성을 잘 고려할 수 있는 KTG 예측 시스템으로 발전시킬 수 있을 것이다.
Acknowledgments
이 연구는 기상청 기상기술개발사업(CATER 2012-2011)의 지원으로 수행되었습니다.
References
-
J. Y. N Cho, E Lindborg, Horizontal velocity structure functions in the upper troposphere and lower stratosphere 1. Observations, J. Geophys. Res, (2001), 106, p10223-10232.
[https://doi.org/10.1029/2000JD900814]

-
J. A Dutton, H. A Panofsky, Clear air turbulence: A mystery may be unfolding, Science, (1970), 167, p937-944.
[https://doi.org/10.1126/science.167.3920.937]

-
G. P Ellrod, P. F Lester, L. F Ehernberger, Clear-air turbulence, Enc. Atmos. Sci.,J. R. Holton et al., Eds., Academic Press, (2003), p393-403.
[https://doi.org/10.1016/B0-12-227090-8/00104-4]

- T. H Fahey, Northwest Airlines atmospheric hazards advisory and avoidance system, Preprints, 5th Conf. on Aviation, Range, and Aerospace Meteorology, Vienna, VA, Amer. Meteor. Soc, (1993), p409-413.
- G. A Grell, J Dudhia, D. R Stauffer, A description of the fifth generation Pen State/NCAT mesoscale model, NCAR Tec Note, NCAR/TN-398+STR, (1994), p138.
-
E. B Jaeger, M Sprenger, A Northern Hemispheric climatology of indices for clear air turbulence in the tropopause region derived from ERA40 reanalysis data, J. Geophys. Res, (2007), 112, pD20106.
[https://doi.org/10.1029/2006JD008189]

- W Jang, H.-Y Chun, J.-H Kim, A study of forecast system for clear-air turbulence in Korea. Part I: Korean Integrated Turbulence Forecasting Algorithm (KITFA), Atmos, (2009), 19, p255-268.
- J.-H Kim, H.-Y Chun, W Jang, R. D Sharman, A study of forecast system for clear-air turbulence in Korea, Part II: Graphical Turbulence Guidance (GTG) system, Atmos, (2009), 19, p269-287.
-
J.-H Kim, H.-Y Chun, Statistics and possible sources of aviation turbulence over South Korea, J. Appl. Meteor. Climatol, (2011a), 50, p311-324.
[https://doi.org/10.1175/2010JAMC2492.1]

-
J.-H Kim, H.-Y Chun, R. D Sharman, T. L Keller, Evaluations of upper-level turbulence diagnostics performance using the Graphical Turbulence Guidance (GTG) system and Pilot Reports (PIREPs) over East Asia, J. Appl. Meteor. Climatol, (2011), 50, p1936-1951.
[https://doi.org/10.1175/JAMC-D-10-05017.1]

- J.-H Kim, H.-Y Chun, Development of the Korean mid-and upper-level Aviation Turbulence Guidance (KTG) system using the regional unified model, Atmos, (2011b), 21, p497-506.
-
J.-H Kim, H.-Y Chun, Development of the Korean Aviation Turbulence Guidance (KTG) system using the operational Unified Model (UM) of the Korea Meteorological Administration (KMA) and Pilot Reports (PIREPs), J. Korean Soc. Aviat. Aeron, (2012), 20, p76-83.
[https://doi.org/10.12985/ksaa.2012.20.4.076]

- P Koch, H Wernli, H. W Davies, An eventbased jet-stream climatology and typology, Int. J. Climatol, (2006), 26, p283-301.
- P. F Lester, Turbulence: A New Perspective for Pilots, Jeppesen Sanderson, (1994), p212.
- J.-S Min, H.-Y Chun, J.-H Kim, An investigation of synoptic condition for Clear-Air Turbulence (CAT) events occurred over South Korea, Atmos, (2011), 21, p69-83.
- I Mason, A model for assessment of weather forecasts, Aust. Meteor. Mag, (1982), 30, p291-303.
- National Transportation Safety Board, U.S. Air Carrier Operations, Calendar Year 2005. Annual review of aircraft accident data, NTSB/ARC-09/01, Washington, DC, (2009), p66.
- R Sharman, C Tebaldi, G Tebaldi, J Wolff, An integrated approach to mid- and upper-level turbulence forecasting, Wea. Forecasting, (2006), 21, p268-287.