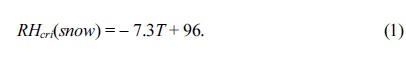A Method for the Discrimination of Precipitation Type Using Thickness and Improved Matsuo’s Scheme over South Korea

1. 서 론

대기 중 발생하는 기상현상은 물의 상변화에 따라 다양한 일기현상이 일어난다(Kim et al., 2003; Hong, 2006). 비, 눈, 진눈깨비와 우박 등의 강수형태는 지표층과 대기층 간 시공간적인 기상조건과 공간분포에 따라 크게 달라진다. 이러한 문제를 극복하고자 수치모델 의존도가 높아지고 있지만, 지표층의 복잡 다양한 비선형방정식의 해를 얻는 데 한계가 있다(Strikwerda, 2004). 눈과 진눈깨비는 하층대기가 영상(0~5^oC)인 경우에도 관측되어 예보관이 겨울철 강수형태를 예보할때 정확도가 떨어지는 요인이 된다. 특히 강수형태 판별 결과가 눈과 비의 혼재구간인 경우, 정확한 강수형태 예보에 어려움이 있다(Lee, 2006).

Stuart et al. (2007)은 강수형태 판단을 위해 관측 자료를 기반한 실황분석, 수치모델과 관측값의 오차 분석, 그리고 수치모델오차를 고려한 예측시나리오를 설계하였다. 강수형태 판별을 위한 선행 연구들은 주로 과거 관측값을 이용한 통계 분석법이었다. 강수형태를 예측하는 데 대표적인 자료는 두 기압면의 높이차이인 층후이다. Bluestein (1993)은 1000~700 hPa 층후값이 2760 gpm일 경우 층후의 평균온도가 264.23 K로서 평균 기온감률을 고려하면 지상기온이 약 0^oC가됨을 보였으며, 2760 gpm의 이하에서는 눈이 내리는 절대구간임을 제시하였다. 현재 한국 기상청에서도 이 방법을 이용하여 1000~700 hPa 층후값 2760 gpm을 눈이 내리는 절대 기준으로 정의하고 있으며, 기준값 2760 gpm 이하에서는 눈, 2820 gpm 이상의 값은 비로 강수형태 예측에 활용하고 있다. 보다 정확한 강수형태를 판별하기 위해서는 강수가 발달하는 층의 높이, 수증기량, 녹는 층의 두께 등을 고려해야 한다. 또한 수치모델 자료를 분석할 때, 산악지역에서 1000hPa 등압면 고도는 지하에 위치하기 때문에, 그 지점의 특성을 반영한 통계 자료로 보정할 필요가 있어, Elliott (1988)는 층후값을 지역별, 지형적 특징을 고려하여 강수형태 예측자료로 제시하였다.

다른 방법으로는 녹는 층 두께를 정의하여 강수형태를 판별할 수 있다. 눈이 내릴 수 있는 녹는 층 최소한의 두께는, 0^oC 이상인 경우 대기상태와 지역에 따라 최소 200 m에서 최대 600 m를 초과할 수 없다고 연구된 바 있다(Weather forecasting handbook, 2002; White et al., 2002; White et al., 2010).

이러한 선행연구에도 불구하고, 실제 예보에 활용하기 위해서는 강수형태 판단이 난해한 대기조건에서 신뢰할 수 있는 상세한 기준이 필요하다. 이러한 요구에 부합하는 방법이 특정 기상요소 간의 상관관계를 이용한 통계기법이다. Matsuo et al. (1981)는 지상의 기온과 습도 관계식으로 강수형태를 판별하였고, 강수형태는 눈, 비, 그리고 진눈깨비였다. Stewart (1992)는 Matsuo 기준을 지역에 맞게 개선하여 수치예측 모델에 적용하였다. 또 다른 연구에서는 2개의 층후 구간을 이용한 Nomogram을 작성하여 강수형태를 구분 하였다(Keeter et al., 1989; Keeter and Cline, 1991; Souza, 1994; Keeter et al., 1995). Bourgouin (2000)은 고층기상관측 자료를 열역학선도에 적용하여 지상과 연직대기온도선 0^oC를 기준선으로 하여, 대기 기온선과의 면적을 양과 음의 값으로 계산한 후, 이를 강수형태 판별에 사용하였다. 또한 Won et al. (2010)은 라디오미터 관측자료로 계산된 3개층의 층후와 지상온도를 이용하여 강설 발생 이전 강설형태에 대한 실황예보가 가능하다는 것을 검증하였으며, Ha et al. (2008)은 국지분석시스템을 이용하여 한국지역 강수유형을 구분하고, 겨울철 북부지역과 서해상을 지나는 저기압에 의한 강수 시, 강수유형 판별에 유용하게 활용 될 수 있음을 보였다.

Fig. 1

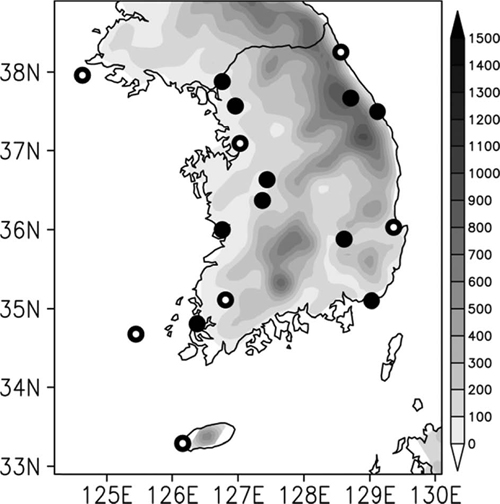
Altidutes and locations of 7 upper-level observation stations (opened circles, December, 2003~March, 2011) and selected 10 surface observation stations (January, 2009~March, 2011) over South Korea.

본 연구의 목적은 한국에 적합한 강수형태 판별법을 제시하는 것이다. 특히, 0^oC의 지상기온을 경계로 예측하기 어려운 강수형태 구분에 초점을 두었다. 연구 내용은 첫째, 우리나라의 지역특성을 고려한 층후값을 제시하고, 둘째, 정의된 층후값에 따라 눈, 비 절대구간 사이에 강수형태가 혼재된 구간을 분석하고, 이를 통계적으로 재분석하여 적설판단 기준을 제시하였다. 셋째, 이를 통해 요약된 강수형태 판단표를 이용한 기상실황 감시 및 강수예측 활용 방법을 제시하였다.

2. 자 료

강수형태의 통계적 분류와 층후 기준값의 설정을 위해 7개 고층관측 지점(속초, 고산, 백령도, 흑산도, 포항, 오산, 광주)에서 총 5년(2003. 12.~2008. 12.) 동안의 자료를 이용하였으며, 설정된 층후 기준값의 검증을 위해 7개 고층관측 지점과 주요 10개 지상관측지점의 3년 동안의 자료(2009. 1.~2011. 3.)를 이용하였다(Fig. 1). 본 연구에서 겨울철은 12월, 1월, 2월, 그리고 3월로 정의하였다. 오산과 광주지점은 1일 4회 6시간 간격(0000, 0600, 1200, 1800 UTC), 나머지 지점은 1일 2회 12시간 간격(0000, 1200 UTC) 고층자료를 이용하였다. 지상관측자료는 강수형태, 지상기온, 상대습도를 사용하였다. 모든 연구사례는 관측시각에 강수현상이 기록된 사례를 대상으로 분석하였다. 주요 10개 지상관측 지점들은 고층관측자료가 존재하지 않기 때문에 강수형태를 판별하기 위해 수치모델 자료를 이용하였다. 분석에 사용된 모델자료는 초단기 기상분석 및 예측시스템(Korea Local Analysis and Prediction System, KLAPS) 재분석장이다. KLAPS 재분석장 격자자료의 시간분해능은 1시간 간격이고, 수평분해능은 5 km 간격으로 동서남북격자(235 × 283)로 구성되어 있으며, 연직분해능은 22층으로 50 hPa 간격이다.

Table 1

Thresholds to be calculated by 1 standard deviation in sleet cases at low-level troposphere using 7 upper-level observation data during winter season from December, 2003 to December, 2008.

3. 층후를 이용한 강수형태 구분

3.2 1000~850 hPa과 1000~700 hPa 층후 비교

층후별 최소(눈 경계), 최대(비 경계)값의 편차가 가장 작은 층후는 1000~850 hPa로 16 gpm 이고, 1000~700 hPa 층후 편차는 48 gpm로서 1000~850 hPa 층후값보다 3배 정도 더 큰 값을 가졌다. 등압면에 따른 기준고도 차는 850 hPa(약 1.5 km)과 700 hPa(약 3.0km)에서 약 2배 차이가 나지만, 층후 편차는 약 3배를 보였다. 두 층간의 기준고도가 높으면 층후편차 값이 커져 강수형태를 판별하는 데 어려움이 따른다. 또한 겨울철 강수형성 과정이 주로 하층대기의 풍향과 풍속에 의존되기 때문에(Lee, 1979; Ho and Kang, 1988; Song, 1993; Jhun et al., 1994), 겨울철 강수형태를 판별하기 위해서는 기준고도 차가 작은 1000~850hPa 층후값을 사용하여 눈과 비를 구분하는 것이 정확성을 높여준다.

Fig. 2

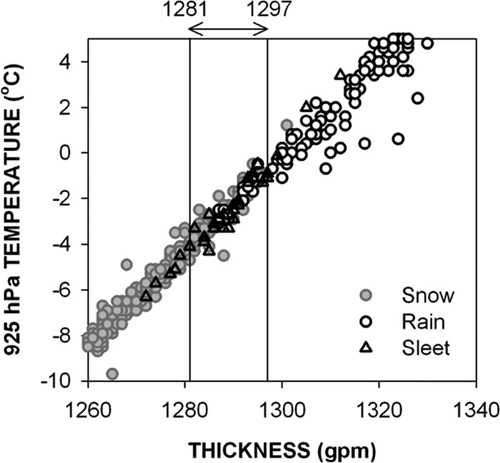
Scatter plots of precipitation type according to 1000~850 hPa thickness (gpm) and 925 hPa temperature (oC) at 7 upper-level observation stations during winter season from December, 2003 to December, 2008. ‘1281’ and ‘1297’ denote 1 standard deviation from average of 1000~ 850 hPa thickness.

Figure 3은 한반도에 눈과 비가 동시에 관측되었던 2개의 사례에 대해 강수형태 실황분포도와 Table 1에서 제시한 1000~700 hPa과 1000~850 hPa 층후 기준 값으로 눈과 비 구간을 비교한 결과이다. Figure 3a는 2010년 1월 4일 0000 UTC 기상실황이다. 전라남도 지역에 비가 내리고 있으며, 1000~700 hPa과 1000~850hPa 두 층후 기준값은 실제 비가 관측된 지역의 북쪽에 위치하였다. 반면 1000~700 hPa 층후의 눈 절대값 경계선은 서울부근에 위치하고, 1000~850 hPa 층후는 충청도 북쪽지역에 놓여있다. 중부지방 전역에서 눈이 관측된 것을 고려하면, 1000~850 hPa 층후의 눈 기준선이 1000~700 hPa 층후의 눈 기준선보다 낮아 중부지방에서 강수형태가 진눈깨비보다 눈으로 구분되어 정확성이 높은 것으로 나타났다. 또한 Fig. 3b는 2010년 2월 11일 0000 UTC 기상실황이다. 남부지방은 비가 오고 있고, 충청도를 포함한 중부지역 위로 눈이 내리고 있다. 1000~700 hPa 층후 기준값으로 강수현상을 판단할 때 충청도 지방은 비 구간에 있으나 1000~850 hPa 층후 기준값은 눈과 비의 혼재구간에 위치한다. 위 사례에서 1000~850 hPa 층후 기준값이 1000~700 hPa 층후 기준값보다 높아 정확성과 혼재구간이 줄어들어 강수형태 판별에 유용하다.

Fig. 3

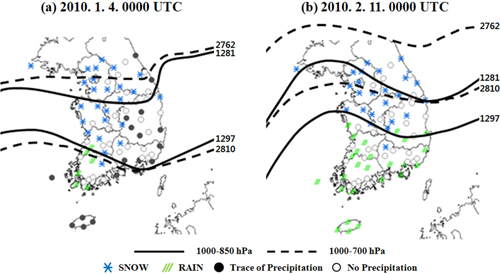
Distributions of weather phenomena, 1000~850 hPa (solid lines) and 1000~700 hPa (dashed lines) thicknesses over South Korea at (a) 4 January and (b) 11 February 2010, respectively.

Table 2

Average of standard deviation of 1000~850 hPa thickness using KLAPS reanalysis data in sleet cases at 10 surface observation stations during winter season from January, 2009 to March, 2011.

4. 혼재구간에서 강수구분 방법

4.1 Matsuo 기준과 개선방법

습윤 대기에서 물의 상변화에 따라 수증기는 승화 되거나 액화되는 과정을 거치면서 최종적인 강수형태는 지면에 도달될 때 결정된다. 물의 상변화는 기온과 습도의 관계이다. Figure 4는 1000~850 hPa 층후에서 눈(1281 gpm)과 비(1297 gpm)의 경계값 사이에 포함된 강수현상을 지상기온과 상대습도의 관계로 분석 하였다. Figures 4a, 4b에서 눈의 경계값은 Matsuo 기준을 준수하였으며, 비의 경계값은 새로운 선형방정식으로 산출하였다. Matsuo 기준은 식 (1)과 같이 상대습도(RH)와 지상기온(T)의 회귀식이며, 눈의 경계치에 해당한다(Matsuo et al., 1981).

Fig. 4

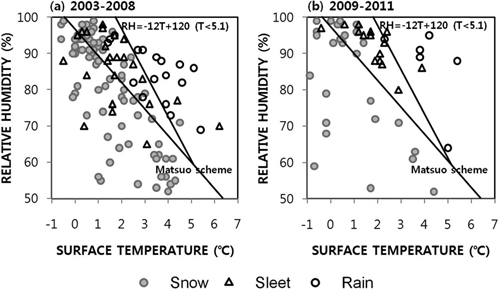
Scatter plots of precipitation type according to surface temperature (oC) and relative humidity (%) at 7 upper-level observation stations during winter season. Left and right hand line denote Matsuo scheme and added linear equation, respectively. (a) Observations from December, 2003 to December, 2008, (b) ones from January, 2009 to March, 2011.

Figure 4a에서 Matsuo 기준의 좌측에는 비 현상이 없으나 우측에는 눈, 진눈깨비 그리고 비 현상이 공존하였다. 강수현상을 좀더 정확하게 구분하고자 새로운 선형방정식 (Eq. 2)을 추가하였다.

여기서 T는 기온이고, RH는 상대습도이다. 제시한 방정식에 따라 Matsuo 기준의 왼쪽은 눈 구역, 추가한 선형방정식의 오른쪽은 비 구역, 가운데 영역은 눈·비·진눈깨비가 혼재된 구간으로 강수현상을 구분할 수 있다. 이 방법으로 검증한 결과가 Fig. 4b이다. 새롭게 제안한 선형방정식 오른쪽에 눈 현상은 전혀 나타나지 않았고 Matsuo 기준의 왼쪽에도 비현상이 나타나지 않았다. 이 두 선형방정식 중간구역에 진눈깨비는 69%로 가장 많았다.

4.2 개선된 Matsuo 기준의 검증 결과

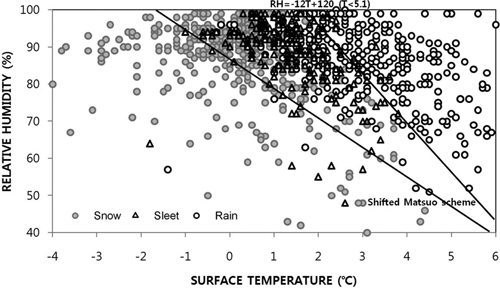
추가된 기준 방정식이 강수형태를 구분하는 새로운 기준이 될 수 있는지를 검증하기 위해 고층관측자료가 없는 지상관측지점들에 대해 KLAPS 재분석장을 이용하여 층후 기준에 따른 강수형태를 조사하였다. 주요 10개 지상관측지점의 3년(2009. 1.~2011. 3.) 동안의 층후(1000~850 hPa) 자료를 이용하였다. 모든 강수사례에 대해 층후는 지상기온과 상대습도에 따른 강수형태 분포도로 나타내었다(Fig. 5). 비 경계선(Eq. 2)의 오른쪽에서는 강수사례의 95%가 비로 관측되었고 진눈깨비 사례가 5%였으며, 눈은 관측되지 않았다. 그러나 Matsuo 기준의 왼쪽은 눈 구역임에도 불구하고 진눈깨비와 비의 강수형태가 27% 존재하였다. 따라서 Matsuo 기준을 우리나라 지역에 적용하기 위해, Fig. 6과 같이 Matsuo 기준을 1.365^oC 왼쪽으로 이동시켰다. 결과적으로 새로운 Matsuo 기준에서 강수형태가 눈인 구역에서는 눈의 관측비율이 89%로 상승했으며, 비는 3%로 감소했다.

Fig. 5

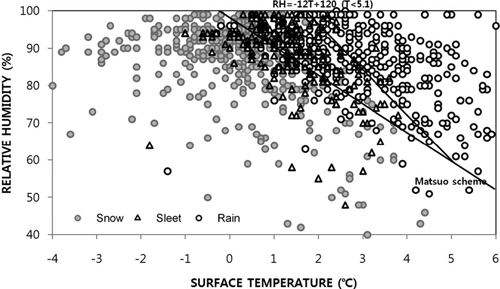
Scatter plots of precipitation type according to surface temperature (oC) and relative humidity (%) at 10 surface observation stations during winter season from January 2009 to March 2011.

Fig. 6

Same as Fig. 5, but for Matsuo scheme to be shifted by 1.365oC from right to left at surface temperature axis.

4.3 설정된 강수형태 판단표

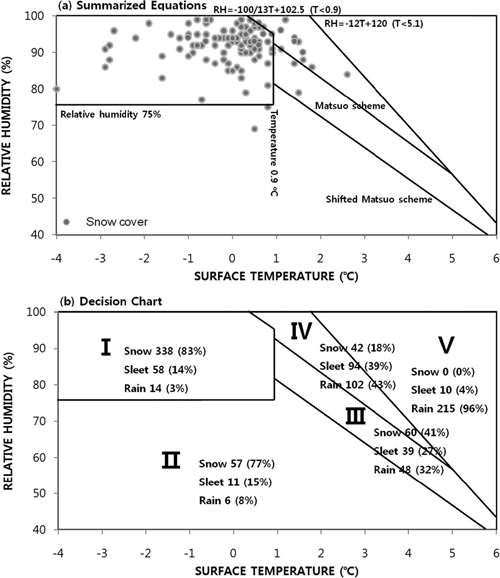
개선한 Matsuo 기준으로 강수형태를 구분하기 위해 Fig. 7a과 같이 설정하였다. 이것을 요약한 Fig. 7b의 구역(적설구역)은 상대습도 75% 이상, 기온 0.9^oC 이하 구역이며, 전체 적설사례 중 88%가 해당하는 구역이다. I, II구역은 모두 눈 구역으로서, 눈이 관측된 사례가 각각 83%, 77%로 가장 높았다. 진눈깨비를 눈에 포함하면 각각 97%, 92%로 더 높게 나타났다. III, IV구역(강수형태 혼재구역)에서 III구역은 눈(41%)이 가장 많이 분포하며, IV구역은 비(43%)가 가장 많이 분포하였다. V구역은 비 구역으로서 비가 96%였다. 결과적으로 강수형태 판단표를 이용해 지상기온과 상대습도만으로 혼재된 구역 내에서 간단하게 눈, 비 그리고 진눈깨비와 적설 판단이 가능함을 제시한다. 예보 적용 시 I, II구역은 눈, III구역은 눈이 우세한 눈비, IV구역은 비가 우세한 비눈, 그리고 V구역은 비 예보에 적용 할 수 있다.

Fig. 7

(a) Summarized equations in each sector, (b) decision chart for determining precipitation type and ratios of them at each sector

5. 결 론

우리나라에 적용가능한 층후자료를 정량적으로 제시하고자, 고층관측자료(2003. 12.~2008. 12.)를 분석하여 눈과 비의 경계값인 층후값을 산출하였다. 조사 결과 1000~850 hPa 층후 경계값은 1281 gpm를 기준으로 그 이하에서 눈 구역과 1297 gpm를 기준으로 그 이상에서 비 구역으로 구분이 가능하였다. 설정된 층후 기준값은 우리나라에서 해발고도가 150 m 이하에 위치한 지점에서 사용이 가능하였고, 주요 10개 지상관측지점에서도 강수형태 구분이 가능한 것으로 검증되었다.

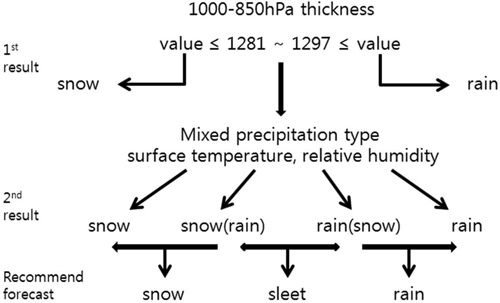
눈과 비가 함께 공존하는 혼재구간에서 보다 세밀하게 강수형태를 판단하고자 새로운 선형방정식과 Matsuo 기준을 개선하여 우리나라 실정에 맞게 적설을 구분할 수 있는 방안을 제시하였다. Table 3은 1000~850 hPa 층후값이 눈 기준값과 비 기준값 사이인 사례일 경우, 강수형태 판별을 계산할 수 있는 알고리즘을 요약한 것이다. Figure 8은 결과를 요약한 강수형태 판단 방법이다. 1000~850 hPa 층후의 보편적인 기준값 1281 gpm보다 작으면 눈, 1297 gpm보다 크다면 비로 판단하면 된다. 그러나 1281~1297 gpm 내에 포함되면 다음단계로 이동하여, 개선된 Matsuo 기준을 이용하여 강수형태를 세분화하였다. Figure 7b에서 제시한 강수형태 판단차트를 참고할 수 있다. 따라서, 시간진행에 따라 눈/비(III)에서 눈(I, II)으로 이동할 것으로 판단되면 눈 예보를, 비/눈(IV)에서 비(V)로 이동할 것으로 판단하면 비 예보를 권장한다. 각 판단 과정에 사용된 알고리즘은 수치예측 자료에 적용이 가능하며, 제시된 강수형태 판단표를 이용하여 예보관은 수치모델과 관측값과의 차이에 따른 보정을 거쳐, 시간진행에 따른 판단과정을 통해 강수형태 예측에 활용할 수 있다.

Table 3

Defined decision chart of precipitation type (I~V) shown in Fig. 7. RH and Tsurface denote relative humidity and surface air temperature, respectively

Fig. 8

Flow chart of recommending forecast for precipitation type according to decision process.

Acknowledgments

본 연구는 국립기상연구소 주요사업 ‘예보기술지원 및 활용연구(NIMR-2012)’의 일환으로 수행되었습니다.

References

• H. B Bluestein, Synoptic-Dynamic Meteorology in Midlatitudes. Vol. 2: Observations and Theory of Weather Systems, Oxford University Press, (1993), p594. [https://doi.org/10.1175/1520-0434(2000)015<0583:AMTDPT>2.0.CO;2]
• P Bourgouin, A method to determine precipitation type, Wea. Forecasting, (2000), 15, p583-592.
• G Elliott, Weather forecasting: Rules, Techniques and Procedures, American Press, Boston, Mass, (1988), p153.
• J. C Ha, Y. H Lee, J. S Lee, H. C Lee, H. S Lee, Estimation of Precipitation Type using Korea Local Analysis and Prediction System, Proceedings of the Spring Meeting of Korea Meteorological Society, (2008), p306-307.
• Paul O. G Heppner, Snow versus rain: looking beyond the “magic” numbers, Wea. Forecasting, (1992), 7, p683-691.
• C. H Ho, I. S Kang, The Variability of Precipitation in Korea, Asia-Pac. J. Atmos. Sci, (1988), 24, p38-48.
• S. G Hong, Weather Analysis and Weather Forecasting, Kyohak Yunkusa Publishing Co, (2006), p530.
• J. G Jhun, D. K Lee, H. A Lee, A Study on the Heavy Snowfalls Occurred in South Korea, Asia-Pac. J. Atmos. Sci, (1994), 30, p97-117.
• K. K Keeter, S Businger, L Lee, J. S Waldstreicher, Winter weather forecasting throughout the eastern united states. part III: The effects of topography and the variability of winter weather in the Carolinas and Virginia, Wea. Forecasting, (1995), 10, p42-60. [https://doi.org/10.1175/1520-0434(1995)010<0042:WWFTTE>2.0.CO;2]
• K. K Keeter, J. W Cline, The objective use of observed and forecast thickness values to predict precipitation type in North Carolina, Wea. Forecasting, (1991), 6, p456-469. [https://doi.org/10.1175/1520-0434(1991)006<0456:TOUOOA>2.0.CO;2]
• K. K Keeter, J. W Cline, R. P Green, Local objective guidance for predicting precipitation type (LOG/PT) in North Carolina - An alternative to MOS guidance. NOAA Tech. Memo, NWSER-82, NOAA/NWS, (1989), p125-135.
• Y. S Kim, K. E Kim, K. J Ha, H. H Um, Essence of Atmospheric Dynamics, Sigmapress, (2003), p303.
• B. S Lee, The Distribution of the Fresh Snowfall in South Korea, Geography education, department of geography, (1979), 9, p224-233.
• W. J Lee, Weather Chart and Weather Analysis, Kwanggyo It’aeks Publising Co, (2006), p97.
• T Matsuo, Y Sasyo, Y Sato, Relationship between types of precipitation on the ground and surface meteorological elements, J. Meteor. Soc. Japan, (1981), 59, p462-476.
• B. H Song, Comparative Study for Snowfalls between East Coast and West Coast Region in South Korea, Master’s Degree Thesis in Seoul Univ, (1993), p32.
• C. A Souza, The impact of Appalachian damming on approaching cyclones and implications for objective weather forecasts. M. S. thesis, Dept. of Meteorology, The Pennsylvania State University, (1994), p179.
• R. E Stewart, Precipitation types in the transition region of winter storms, Bull. Amer. Meteor. Soc, (1992), 73, p287-296. [https://doi.org/10.1175/1520-0477(1992)073<0287:PTITTR>2.0.CO;2]
• J. C Strikwerda, Finite difference schemes and partial differential equations, 2^nd Ed., Society for Industrial Mathematics, (2004), p165-170.
• N. A Stuart, D. M Schultz, G Klein, Maintaining the role of humans in the forecast process, Bull. Amer. Meteor. Soc, (2007), p1893-1898.
• Weather forecasting handbook, Precipitation type of winter forecasting, (2002), p144.
• A. B White, D. J Gottas, A. F Henkel, P. J Neiman, F. M Ralph, S. I Gutman, Developing a performance measure for snow-level forecasts, J. Hydrometeor, (2010), 11, p739-753. [https://doi.org/10.1175/2009JHM1181.1]
• A. B White, D. J Gottas, E. T Strem, F. M Ralph, P. J Neiman, An automated brightband height detection algorithm for use with Doppler radar spectral moments, J. Atmos. Oceanic Technol, (2002), 19, p687-697. [https://doi.org/10.1175/1520-0426(2002)019<0687:AABHDA>2.0.CO;2]
• H. Y Won, Y. H Kim, D. E Chang, Determination and predictability of precipitation-type in Winter from a ground-based microwave radiometer profiler radiometer, Atmosphere, (2010), 20, p229-238.