PNU CGCM과 WRF를 이용한 남한 지역 기온 예측성 검증

1. 서 론

장기 기상 및 기후 예측을 위해서는 열용량이 큰 해양의 상태를 예측하는 것이 매우 중요한데, 해양의 상태는 대기와 해빙 등 지구 아시스템(subsystem)들과의 상호작용에 의해 결정된다. 따라서 정확한 장기 예측을 위해서는 지구 아시스템들의 상호작용을 고려하는 접합대순환모형의 사용이 필수적이다(Meehl and Washington, 1995; IPCC, 2014).

그 동안 중장기 계절예측의 정확성을 향상시키기 위한 연구가 국내·외에서 활발히 진행되고 있다. 예를 들어 MacLachlan et al. (2015), Jung et al. (2015), Lee et al. (2016)은 GloSea5 (Global Seasonal forecast system version 5)를 이용하여 대기의 주요 경년 변동 모드인 El Niño Southern Oscillation (ENSO), North Atlantic Oscillation (NAO), Arctic Oscillation (AO)의 성능을 검증하거나, Indian Ocean Dipole (IOD), 몬순 지수 등과 같은 주요 지수들을 통하여 GloSea5의 6개월 기후 예측 능력을 평가하였다. 또한, Ahn et al.(2012), Sun and Ahn (2015), Ahn and Lee (2015), Kim and Ahn (2015)는 PNU CGCM (Pusan National University Coupled General Circulation Model)을 이용하여 12개월 앙상블 예측 시스템을 개발하고 검증하였으며, AO의 예측성을 평가하였고 지면 초기조건 및 해양 자료동화에 따른 북반구 겨울철 기온과 해수면 온도의 예측성을 연구하였다.

한반도의 경우 산악 지형이 많고 해안선이 복잡하여 다양한 규모의 기상현상이 복합적으로 나타나므로, 전지구 접합대순환모형(Coupled General Circulation Model, CGCM)을 이용한 기후 예측을 하는 것에 한계가 있다(Hong and Kanamitsu, 2014). 이러한 한계를 극복하고자 지역기후모형(Regional Climate Model, RCM)을 통한 역학적 규모축소법을 이용하여 고해상도의 기후 자료를 생산하는 방법들이 이용되고 있다. 또한 지역기후모형의 특징을 파악하고 모형을 개선하는 연구가 활발하게 진행되고 있다(Im et al., 2008; Lee et al., 2013; Ahn et al., 2016b). Ahn et al. (2014)과 Lee et al. (2014)은 각각 WRF와 GRIMs-RPM을 이용하여 21세기 한반도 및 동아시아 기후변화를 RCP 4.5, 8.5 시나리오를 적용하여 전망하였고, Im et al.(2015)는 HadGEM2-AO를 WRF의 초기조건으로 처방하여 RCP 시나리오에 따른 남한 지역의 기후를 전망하기도 하였다. 또한, Ahn et al. (2016b) 및 Lee et al.(2017)은 Multi-RCM을 이용하여 남한 지역이나 동아시아 지역의 여름철 강수 및 극한 강수 변화를 RCP 시나리오에 적용시켜 전망했다. Im et al. (2017)은 미래 기후에서의 남한 지역 heat stress 변화에 대하여 연구하기도 하였다. Lee and Hong (2014)은 지역기후 모형의 공간해상도 증가에 따른 한반도 영역의 극한기후 모의 능력 상승에 대해 연구하였다. 이 밖에도 Ahn et al. (2016a), Hur and Ahn (2017)은 WRF를 사용하여 동아시아 농업기후를 전망하거나 Multi-RCM을 이용하여 한반도 주요 과수작물의 개화일을 예측하는 등 지역기후모형은 한반도 영역에 대한 다양한 분야의 연구에서 사용되어왔다.

상세 장기 예측을 수행함에 있어서 CGCM의 해상도 한계와 RCM의 장기 예측성의 한계를 동시에 극복하기 위해서는 CGCM과 RCM의 chain을 통한 예측이 필요하다. Kim et al. (2011)의 연구에서는 AGCM(Atmospheric General Circulation Model)인 GDAPS(Global Data Assimilation and Prediction System)와 RCM인 RegCM3 (Regional Climate Model 3)를 이용하여 3개월의 계절예측을 수행하였으며 남한지역 겨울철에 대해 분석하였다. Ratnam et al. (2017)은 Scale Interaction Experiment (SINTEX)-Frontier Research Center for Global Change (FRCGC) version 2.0 (SINTEX-F2v)을 WRF를 통해 역학적 규모축소하여 남반구 여름철 호주의 기후 예측을 하였다. 선행연구에서는 특정 계절에 대한 예측 및 분석을 수행한 것이므로 CGCM-RCM chain을 이용하여 매달의 초기조건으로부터 상세 장기 예측을 실시하고 검증한 연구는 국내·외적으로 부재하다. 본 연구에서는 PNU CGCM을 이용하여 적분한 전지구 장기 예측 결과를 지역기후모형인 WRF의 초기 및 경계조건으로 처방하여 한반도 지역에 대해 고해상도의 예측 자료를 생산하고, 남한 지역 평균 기온의 예측성능을 살펴보고자 한다.

2. 자료 및 방법

2.1 전지구 접합대순환모형

본 연구에서 사용된 전지구 접합대순환모형은 PNU CGCM (Pusan National University Coupled general circulation model; Sun and Ahn, 2011, 2015; Ahn and Lee, 2015)이다. PNU CGCM은 APEC Climate Center (APCC)의 장기예측을 위한 다중모형 앙상블(Multi-Model Ensemble) 시스템의 참여모형이다. 각 성분 모형인 NCEP Community Climate Model version 3 (CCM3; Kiehl et al., 1996) AGCM, GFDL Modular Ocean Model version 3 (MOM3; Pacanowski and Griffies, 2000) OGCM, Los Alamos National Laboratory (LANL) Elastic-Viscous-Plastic Model (EVP) Sea-Ice Model (Ahn and Lee, 2001)으로 구성된다.

대기 성분 모형 CCM3는 T42의 수평해상도(동서방향 2.8125^o)를 가지며 연직으로는 18층으로 구성된다. 해양 성분 모형 MOM3는 CCM3와 같은 2.8125^o의 동서방향 해상도를 가지고 있고 남북방향으로는 저위도에서는 ~0.7^o, 중위도에서는 ~1.4^o, 고위도에서는 ~2.8^o의 가변 격자를 가지고 있으며 연직으로는 40층으로 구성된다. PNU CGCM의 성분 모형 및 해상도에 대한 정보는 Table 1에 나타내었다.

Table 1.

Description of PNU-CGCM.

PNU CGCM의 대기 초기장은 NCEP Reanalysis 2자료를 이용하여 생산하였으며, AMIP-type 적분을 통해 지면 초기장을 생산하였다. 해양 초기장은 Global Ocean Data Assimilation System (GODAS)의 자료를 사용했으며, Variational Analysis using a Filter (VAF)로 해양의 각 40층에 대하여 자료동화를 적용하였다. PNU CGCM에 사용되는 대기, 해양 및 지면 초기장 생산 방법에 대한 자세한 설명은 Ahn and Lee (2015)에 나타나 있다.

2.2 지역기후모형

지역기후모형으로는 WRF version 3.5 (Weather Research and Forecasting model; Skamarock et al., 2008)을 사용하였다. WRF 적분의 수평해상도는 5 km로 한반도를 포함하는 동서방향 150개, 남북방향 245 개의 격자로 구성된다(Fig. 1). 사용된 물리 방안은 구름물리 과정에 WRF Single-Moment 3-class (WSM3) scheme (Hong et al., 2004), 단파복사 모수화에 Dudhia scheme (Dudhia, 1989), 장파복사 모수화에 Rapid Radiative Transfer Model (RRTM) scheme (Mlawer et al., 1997), 지표층에 Monin-Obukhov scheme (Paulson, 1970), 지면 과정에 Noah Land-Surface Model (Chen and Dudhia, 2001), 행성 경계층에 Yonsei University (YSU) scheme (Hong et al., 2006), 적운 모수화에 Kain-Fritsch scheme (Kain, 2004)이다(Table 2).

Fig. 1.

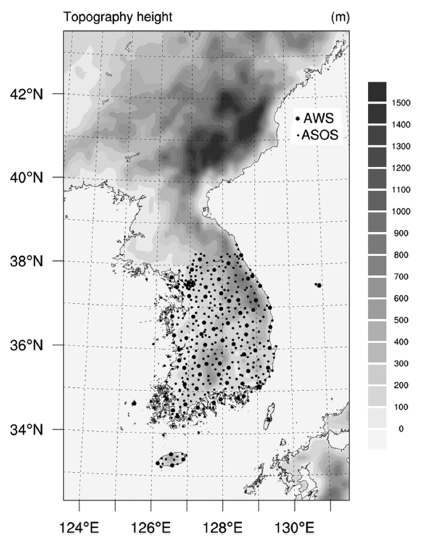
The topography heights (in meters) of the WRF domain and locations of ASOS (bigger dots) and AWS (smaller dots) in South Korea.

Table 2.

WRF configuration used in this study.

2.3 실험 방법

본 연구에서는 PNU CGCM으로 전구 예측자료를 생산하고 그 결과를 초기 및 경계조건으로 하여 WRF로 한반도 지역에 대한 역학적 규모축소를 수행함으로써 남한 지역 상세 예측자료를 생산하였다. PNU CGCM은 매월 초기화하여 5개월의 lead (lead 0~lead 4)로 적분을 수행하였다. 본 논문에서는 1월 초기장으로부터 예측을 시작(RUN)하는 적분을 01RUN, 2월 초기장으로부터 시작하는 적분을 02RUN 등으로 명명하기로 한다. PNU CGCM을 이용한 Hindcast는 2007년부터 2017년까지 11년에 대해 수행하였으며 시간별(hourly)로 자료를 생산하였다. PNU CGCM의 적분 결과는 역학적 규모축소를 하는 lead 2~lead 4에 대해서만 분석하였다(Fig. 2).

Fig. 2.

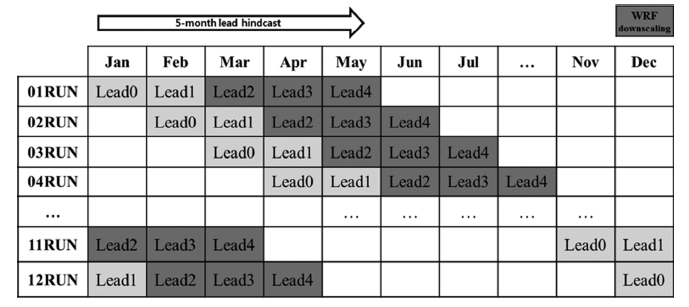
Lead-times in 5-month lead hindcast experiment. Left column indicates initialized month and top line indicates predicted month. Lead2~4 (dark-gray shaded) are dynamically downscaled by WRF.

WRF는 PNU CGCM의 hindcast 결과 중 매달 시작된 적분의 lead 2~lead 4에 대하여 역학적 규모축소를 하였으며, 각 lead의 1일부터 1개월의 연속 적분을 하였고 4일의 spin-up을 수행하였다. 예를 들어 01RUN의 경우 2007~2017년 3월과 4월, 5월에 대해 WRF 적분을 수행하며, 적분 시작일은 spin-up을 위해 각각 2월 25일(윤년의 경우 26일), 3월 28일, 4월 27일이다. PNU CGCM의 결과로부터 생산된 경계조건은 WRF 적분에 1시간 간격으로 처방되고, 후처리를 통하여 일별(daily) 자료를 생산하였다. WRF의 적분 결과도 매달 생산된 lead 2~lead 4에 대하여 분석하였다.

본 연구에서는 남한 지역의 일평균 기온 예측성 검증을 위하여 기상청의 72개 지점의 ASOS (Automated Surface Observing System)와 352개 지점의 AWS (Automatic Weather System) 자료를 사용하였다(Fig. 1). 자료 기간은 2007년부터 2017년까지의 일평균 기온 자료이다. 또한 PNU CGCM과 WRF의 모의성능 검증을 위한 재분석 자료로 NCEP/DOE (National Centers for Environmental Prediction/Department of Energy) Reanalysis 2 (Kanamitsu et al., 2002, 이하 NCEP-R2) 지표면 기온자료를 사용하였으며, 자료 기간은 2007년부터 2017년이다. 검증을 위하여 시간상관계수(Temporal Correlation Coefficient; TCC), 평균제곱근오차(Root Mean Square Error; RMSE) 및 Heidke 기술 점수(Heidke Skill Score; HSS), 적중률(Hit Rate; HR), 오경보율(False Alarm Rate; FAR) 등의 Skill Score들을 활용하였으며, 모형 적분 결과 및 관측의 아노말리에 대해 검증하였다. 각 Skill Score들은 관측자료와 WRF 적분결과의 아노말리를 ± 0.43σ(Standard deviation) 기준으로 normal, above normal, below normal으로 나누어 예측성을 평가하였다(Wilks, 1995).

3. 예측성 평가

3.1 PNU CGCM과 WRF의 모의 성능

CGCM-WRF chain에 의한 예측성 검증에 앞서 PNU CGCM과 WRF의 모의 성능을 검증하였다. Figure 3은 PNU CGCM과 WRF에서 모의된 1, 4, 7, 10월의 평균 기온 공간분포를 NCEP-R2와 함께 나타낸 그림이다. 각 월은 lead time 2의 적분 결과이며, 2007~2017년의 Hindcast에 대한 기후값이다. 각 그림의 오른쪽 상단에 표기한 값은 남한 지역 평균기온의 영역 평균값(33.5-39^oN, 125-130^oE)이다. 먼저 PNU CGCM의 공간 분포를 살펴보면(Figs. 3e-h), PNU CGCM에서 모의한 1월, 4월, 7월, 10월 남한 지역 평균기온은 각각 1.13^oC, 8.40^oC, 23.21^oC, 15.89^oC로 NCEP-R2 (Figs. 3a-d)의 남한 지역 평균기온(1.03^oC, 11.01^oC, 23.57^oC, 16.43^oC)과 마찬가지로 계절에 따른 기온 특성이 잘 나타난다. 남북 기온 경도도 잘 나타나며 특히 1월과 10월은 4월과 7월에 비해 위도에 따른 기온 분포가 더 뚜렷하게 나타나는데, 이러한 특징은 NCEP-R2와 일치한다. 하지만 PNU CGCM은 전지구 규모이므로 한반도의 상세한 지형적 특징을 해상도 내에 모의하는데 한계가 있다. WRF의 결과(Figs. 3i-l)에서는 보다 상세한 기온 분포가 나타난다. 한반도의 경우 북동부지역의 개마고원으로부터 동부지역을 따라 태백산맥이 위치하는 동고서저의 지형적 특징이 있다. WRF에서 모의된 기온은 위도에 따른 분포뿐만 아니라 지형적 특성에 따른 분포도 잘 나타난다. 고도 및 위도에 따른 기온의 분포는 겨울철인 1월에서 가장 뚜렷하게 나타나는데, 이러한 특징은 NCEP-R2의 1월 기온 분포(Fig. 3a)와 한국 기후도(KMA, 2012)의 기온 기후값(1981~2010) 분포에서도 유사하게 나타난다. WRF에서 모의한 4월과 10월의 남한 지역 평균기온은 각각 8.65^oC, 16.56^oC로 PNU CGCM에 비해 평균기온을 높게, 1월과 7월의 남한 지역 평균기온은 각각 −0.06^oC, 21^oC로 PNU CGCM에 비해 낮게 모의하지만 전반적인 기온 분포, 계절적 특성과 남한 영역 평균값이 NCEP-R2 및 PNU CGCM과 유사하게 나타난다.

Fig. 3.

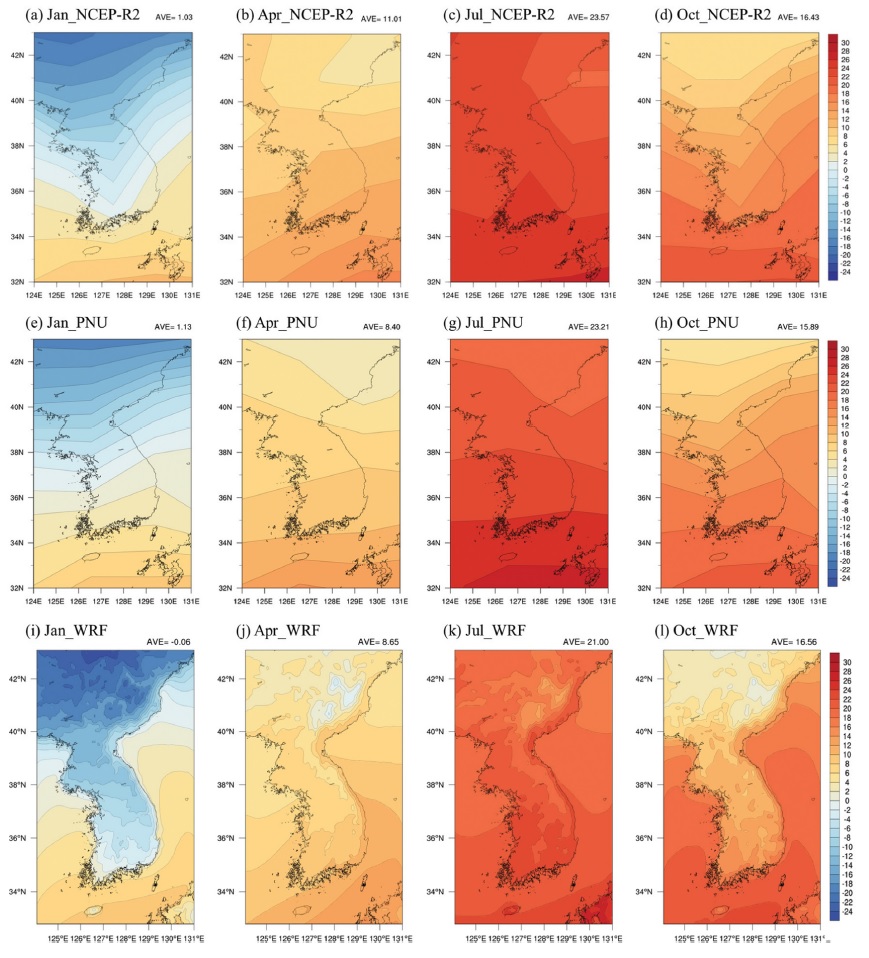
Spatial distribution of mean temperature (oC) derived from NCEP-R2 (upper), PNU CGCM (middle) and WRF (bottom) in the WRF domain for the period of hindcast (2007~2017).

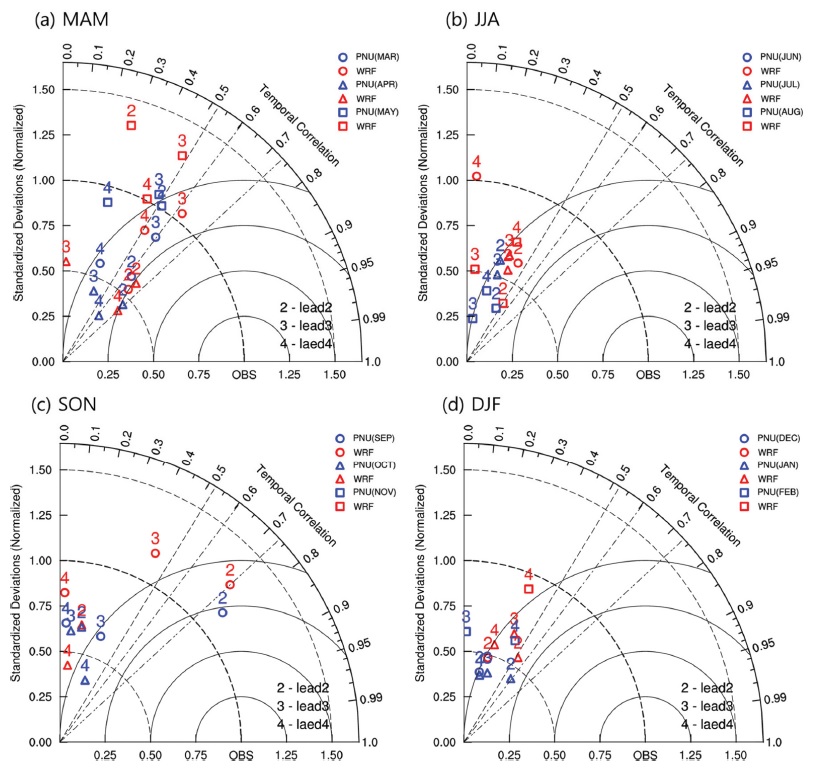
Figure 4는 남한 지역 평균기온에 대한 PNU CGCM과 WRF의 모의성능을 계절별로 나타낸 Taylor 다이어그램이다. 관측 표준편차에 대한 모형의 표준편차비(Normalized Standardized Deviations, NSD) 및 TCC (Temporal Correlation Coefficient)를 나타낸 그림으로 1에 가까울수록 관측과 비슷함을 의미한다. 즉, 그림에서 OBS로 표시되어있는 점에 가까울수록 모의성능이 우수한 모형이다(Taylor, 2001). TCC의 90%(0.521), 95% (0.602), 99% (0.735) 신뢰수준은 파선으로 표시하였다. 전반적으로 관측과 비교한 WRF와 PNU CGCM의 모의 수준은 유사하게 나타나나, 관측과의 상관성은 PNU CGCM보다 WRF에서 다소 높게 나타나고, 기온의 변동성은 WRF가 PNU CGCM에 비해 더 크게 모의한다. 계절별 모의 특성을 살펴보면, 봄철 평균기온의 경우 PNU CGCM과 WRF의 TCC가 신뢰수준 90% 또는 95% 이상인 지점에 많이 분포하여 관측과 관련성이 높은 편이고, NSD는 비교적 1 근처에 많이 분포하여 변동성이 관측과 유사하게 나타난다. 여름철 평균기온의 경우 NSD가 6월의 lead 3 WRF 결과를 제외하고 모두 0.75 미만으로 변동성이 관측에 비해 작고, TCC는 PNU CGCM은 모든 경우, WRF는 8월의 lead 2를 제외한 모든 경우에 신뢰수준 90% 이하로 낮게 나타난다. 가을철에도 전반적으로 기온의 변동성이 관측보다 낮고, TCC도 0.5 이하로 나타나나, 9월의 경우에는 PNU CGCM과 WRF의 lead 2 에서 관측과의 상관성이 각각 99% 신뢰수준 이상인 0.782, 0.734로 12개월 중 가장 높게 나타난다. 겨울의 평균기온 변동성은 WRF와 PNU CGCM 모두 NSD가 1 이하로 관측보다 작게 나타나고 TCC도 1월 lead 2를 제외하고 PNU CGCM과 WRF에서 모두 0.5 미만으로 나타난다. 따라서 WRF가 PNU CGCM 결과를 잘 따라가면서 유사하게 모의하나 WRF에 의해 모의된 자료는 지역적 특성을 잘 반영하여 PNU CGCM에 비해 다소 예측성이 높게 나타나며, 3~5월(봄철)과 9월의 평균기온의 모의 성능이 다른 달보다 높음을 알 수 있다.

Fig. 4.

Taylor Diagram of surface temperature (oC) for the period of hindcast (2007~2017) during (a) MAM, (b) JJA, (c) SON and (d) DJF for 2~4 month lead-times.

3.2 WRF의 예측성 평가

Figure 5는 WRF 아노말리와 관측 아노말리의 TCC와 RMSE를 나타낸 그림이다. 각각의 실선들은 lead 2에서 lead 4까지의 결과를 연결하여 나타냈으며, TCC(Fig. 5a)의 경우 통계적으로 95% (90%) 유의한 경우 채워진 원(빈 원)으로 표시하였다. 예를 들어 TCC 결과의 가장 왼쪽의 실선을 살펴보면 01RUN의 TCC를 lead 2(3월)에서 lead 4(5월)까지 나타낸 것이며 lead 2(3월)의 TCC는 95% 신뢰수준에서 통계적으로 유의함을 의미한다. RUN 별 예측성을 살펴보면 01RUN, 02RUN, 06RUN, 07RUN 그리고 11RUN의 lead 2에서 TCC가 통계적으로 90% 이상 신뢰수준으로 높게 나타난다. 02RUN, 06RUN, 07RUN 그리고 08RUN에서는 lead time이 증가함에 따라 TCC가 낮아졌고, 나머지 RUN들은 lead time이 증가함에 따라 TCC가 높아지거나, 불규칙한 패턴이 나타난다. 3~4월을 예측하는 01RUN과 02RUN에서는 TCC가 비교적 높게 나타나고, 10~12월을 예측하는 8RUN, 09RUN 그리고 10RUN에서는 TCC가 비교적 낮게 나타난다.

Fig. 5.

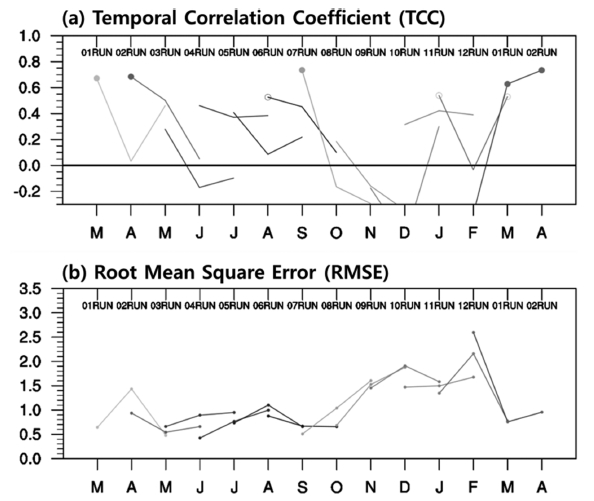
The (a) temporal correlation coefficient (TCC) and (b) root mean squared error (RMSE) of WRF prediction result. The upper x-axis indicates initialized month, lower x-axis indicates predicted month. Each line indicates prediction from lead-time 2 to lead-time 4 of initialized month. Filled (open) circle of (a) TCC indicates the values that are statistically significant at the 95% (90%) confidence level.

RMSE (Fig. 5b)는 0에 가까울수록 예측성이 높음을 의미한다. RUN별 예측성을 살펴보면 03RUN, 04RUN, 07RUN, 08RUN, 09RUN 그리고 10RUN이 lead 2에서 가장 낮은 RMSE를 보인다. 이 RUN들 중 09RUN을 제외한 나머지 RUN들은 lead time이 증가함에 따라 RMSE가 증가한다. 이 밖에 lead time이 증가함에 따라 06RUN은 RMSE가 감소하고, 01RUN, 02RUN, 05RUN, 11RUN, 12RUN은 RMSE가 증가하다가 감소하는 등 불규칙한 패턴을 보인다.

RMSE는 겨울 예측 결과를 제외하면 전반적으로 1.5 미만으로 비교적 낮은 값을 나타낸다. TCC와 RMSE를 종합해보면, WRF 예측성의 변화는 lead time의 영향 보다는 계절 및 월별(10~12월) 영향이 더 큰 것으로 보인다. 이와 같은 특징은 Ahn et al. (2012)에서도 유사하게 나타난다.

Figure 6은 WRF의 HSS, HR, FAR을 나타낸 그림이다. Figure 5와 마찬가지로 각각의 실선들은 lead 2에서 lead 4까지의 결과를 연결하여 나타냈다. HSS는 정확한 예측일수록 1의 값을 가지며, 0은 no skill을 나타낸다. HSS 역시 RUN별로 살펴보면 01RUN, 02RUN, 04RUN, 06RUN, 07RUN, 08RUN 그리고 11RUN에서 lead 2의 예측성이 lead 3과 lead 4에 비해 상대적으로 좋게 나타난다. 07RUN과 11RUN은 lead time이 증가할수록 HSS가 감소하는 모습을 보이고, 01RUN, 02RUN, 04RUN, 08RUN 그리고 12RUN은 lead 3까지는 HSS 값이 감소하다가 lead 4까지는 HSS 값이 다시 증가하는 모습을 보인다. HSS는 다른 검증 결과들과는 다르게 계절 및 월별 특성이 뚜렷하게 나타나지 않았고, 03RUN, 05RUN, 09RUN 그리고 10RUN을 제외한 모든 RUN의 lead 2에서 0.25 이상으로 예측성이 비교적 높게 나타난다.

Fig. 6.

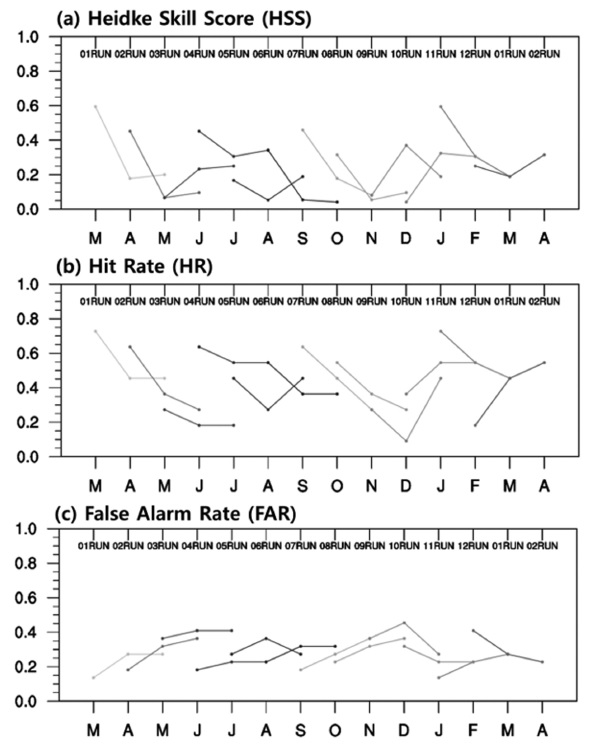
Same as Fig. 5 but for (a) Heidke Skill Score (HSS), (b) Hit Rate (HR) and (c) False Alarm Rate (FAR).

Figure 6b-c는 HR과 FAR을 나타낸 그림이다. HR이 높으면서 FAR이 낮을수록 예측성이 좋음을 의미한다. Figure 6b와 6c를 살펴보면, HR과 FAR은 05RUN, 09RUN, 10RUN 그리고 12RUN을 제외한 모든 RUN의 lead 2에서 상대적으로 높은 예측성을 보인다. 01RUN, 02RUN, 03RUN, 04RUN, 06RUN, 07RUN, 08RUN 그리고 11RUN은 lead time이 증가함에 따라 HR (FAR)이 낮아(높아)지거나 같다. 나머지 RUN들의 HR과 FAR은 lead time의 증가에 따라 불규칙한 변화를 보인다. HR (FAR)은 03RUN과 09RUN 등을 제외한 거의 대부분의 RUN에서 0.35 이상(미만)의 점수를 나타내며, 예측성이 높게 나타난다.

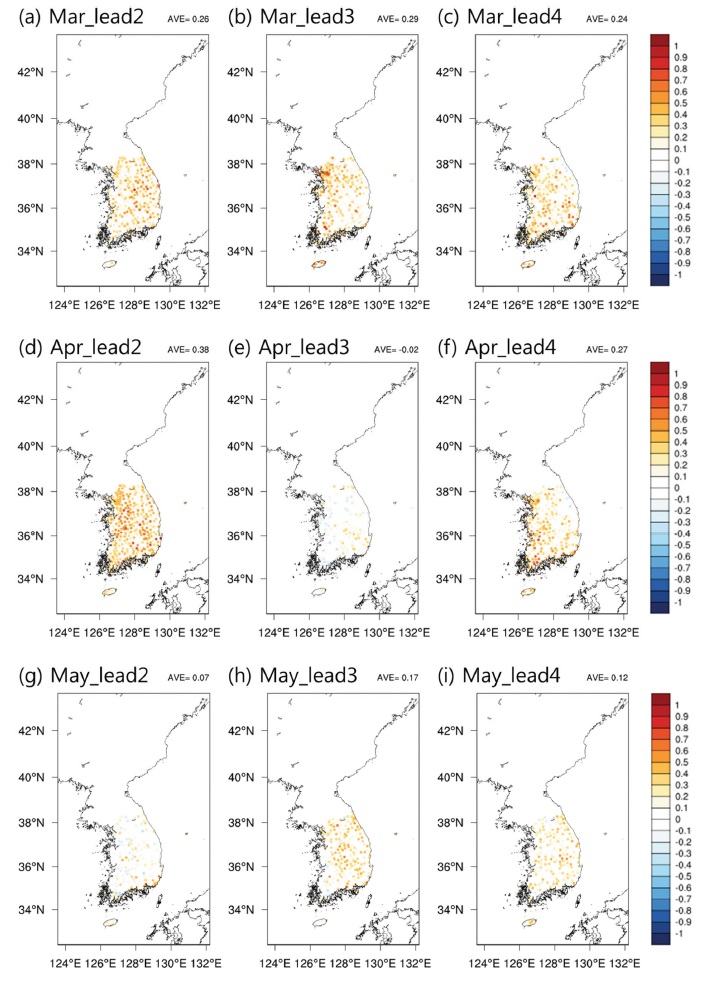
앞의 분석에서 예측성이 가장 높았던 봄철(3~5월)에 대하여 각 lead 별 HSS의 분포를 Fig. 7에 나타냈다. 3월(Fig. 7a-c)은 lead 2, lead 3, lead 4 모두 지역별로 고른 HSS 분포를 보이며, 지점 평균값은 각각 0.26, 0.29, 0.24로 나타난다. 4월(Fig. 7d-f)의 경우 lead 2에서는 대부분의 지역에서 양의 HSS를 보이나, lead 3에서는 경상도 지역 및 강원 북부, 경기도 북서부 지역을 제외하고는 0 이하의 HSS를 보인다. 그러나 lead 4에서는 강원도 동부 및 내륙지역을 제외하고 0 이상의 HSS를 보인다. 4월의 지점 평균값은 lead 2~4에 대하여 각각 0.38, −0.02, 0.27으로 나타난다. 5월(Fig. 7g-h)은 앞의 두 달과는 달리 lead 2에서 가장 낮은 HSS가 나타나며 HSS가 높거나 낮은 지점이 남한 전역에 산발적으로 분포한다. Lead 3의 경우 서부 및 남서부 지방을 제외하고 양의 HSS가 나타난다. Lead 4에서는 일부 0 이하의 HSS가 나타나는 지역이 존재하나 대부분의 지역에서 양의 HSS를 보인다. 종합적으로 살펴보면 남한 지역 내의 예측성은 지형의 영향을 받지 않고 전체 지역에 걸쳐 고르게 나타나는 경향이 있다. 또한 같은 RUN (Figs. 7a, e, i)인 경우에도 lead time이 변함에 따라 예측성이 낮은 지역이 특정 지역에만 국한되어 있지는 않은 것으로 보인다.

Fig. 7.

Spatial distribution of Heidke Skill Score (HSS) for surface temperature in March (top), April (middle) and May (bottom). The values at the top right of each figure are mean HSS.

4. 요약 및 결론

정확한 장기 예측을 위해서는 대기-해양 상호작용을 고려하는 접합대순환 모형의 사용이 필수적이다. 하지만 접합대순환모형은 전지구 규모이므로 한반도의 상세한 지형적 특징을 해상도 내에 모의하는데 한계가 있다. 본 연구에서는 이를 극복하고자 PNU CGCM으로부터 생산된 자료를 초기 및 경계 조건으로 처방한 WRF를 통해 한반도 지역에 대한 고해상도의 예측자료를 매달 준실시간 생산하고 이를 검증하고자 하였다.

PNU CGCM과 WRF가 모의한 한반도 영역의 평균기온 공간분포와 Taylor 다이어그램 분석을 수행한 결과 PNU CGCM과 WRF의 모의 수준이 유사하지만, WRF 결과에서 상세한 지역적 특성이 더 잘 나타났으며 관측과 상관성을 더 높게 모의하는 것을 확인하였다. PNU CGCM은 남한 지역 평균기온의 계절에 따른 기온 특성과 남북 기온 경도는 잘 모의하지만, 한반도의 상세한 지형적 특성은 잘 나타나지 않았다. 반면, WRF에서 모의된 기온은 위도에 따른 분포뿐만 아니라 지형적 특성에 따른 분포도 잘 나타났으며, PNU CGCM과 기온의 분포 및 계절적 특성 등이 전반적으로 유사하게 나타났다. Taylor 다이어그램 분석에서 관측과 비교한 WRF와 PNU CGCM의 모의 수준은 전반적으로 유사하게 나타났으나, 관측과의 TCC는 PNU CGCM보다 WRF에서 다소 높고, 기온의 변동성은 WRF가 PNU CGCM에 비해 관측과 유사하게 모의했다. 계절별로 분석해본 결과, PNU CGCM과 WRF에서 모의된 평균 기온의 예측성은 봄철에 가장 높게 나타났다.

TCC와 RMSE를 통해 살펴본 WRF의 RUN 별 예측성은 대체적으로 lead time이 증가함에 따라 불규칙한 패턴을 보였다. 하지만 01RUN의 lead 2(3월)과 02RUN의 lead 2(4월) 등에서 예측성이 높았고, 10~12월에 대해서는 RUN에 관계없이 예측성이 낮았다. 이는 WRF 예측성의 변화가 lead time의 영향보다 계절 및 월별 영향을 더 크게 받은 것으로 사료된다. Skill Score들을 통해 살펴본 WRF의 RUN 별 예측성은 lead time의 증가에 따라 예측성 변화가 불규칙하게 나타났지만 대부분의 RUN에서 0.25 이상의 비교적 높은 HSS 값을 나타냈고, 0.35 이상(미만)의 비교적 높은(낮은) HR (FAR) 값을 나타내면서 예측성이 높게 평가되었다. 비교적 예측성이 높게 나타났던 봄철 HSS의 공간분포를 살펴보면 나타나 있다. 예측성이 특정 지역에만 편중되어 있지 않고 남한 전체 영역에 걸쳐 고르게 나타나는 특징이 있었다.

동아시아지역의 기후는 큰 계절 변동성을 가지기 때문에 시간에 따른 편차가 크므로 다른 여러 기후 모델에서도 동아시아지역의 예측성이 낮은 것으로 알려져 있다(Wang et al., 2009; Lee et al., 2011; Jung et al., 2015). 본 연구에서는 전지구 접합대순환 모형의 결과를 역학적 규모축소하여 평균 기온에 대한 예측을 수행한 결과 통계적으로 유의한 예측성이 나타나기도 하였다. 그러나 예측 영역이 남한 지역을 대상으로 살펴봤을 뿐만 아니라 분석 기간이 11년(2007~2017)으로 기후를 분석하기에는 다소 짧고 적분 초기장으로부터 2개월 뒤인 lead 2부터 살펴봤기 때문에 한계가 있다. 향후 연구에서 hindcast 기간을 늘리고, 앙상블 예측기법 등을 활용한다면 더 정확하고 높은 예측성능을 얻을 수 있을 것으로 사료된다.

Acknowledgments

본 성과물은 농촌진흥청 연구사업(세부과제번호: PJ01229302)의 지원에 의해 이루어진 것임. 본 논문의 개선을 위해 좋은 의견을 제시해 주신 두 분의 심사위원께 감사를 드립니다.

References

• Ahn, J.-B., and J. A. Lee, (2001), Numerical study on the role of sea-ice using ocean general circulation model, J. Korean Soc. Oceanogr., 6, p225-233, (in Korean with English abstract).
• Ahn, J.-B., and J. Lee, (2015), Comparative study on the seasonal predictability dependency of boreal winter 2 m temperature and sea surface temperature on CGCM initial conditions, Atmosphere, 25, p353-366, (in Korean with English abstract). [https://doi.org/10.14191/Atmos.2015.25.2.353]
• Ahn, J.-B., S.-B. Lee, and S.-B. Ryoo, (2012), Development of 12-month ensemble prediction system using PNU CGCM V1.1, Atmosphere, 22, p455-464, (in Korean with English abstract). [https://doi.org/10.14191/Atmos.2012.22.4.455]
• Ahn, J.-B., Y.-W. Choi, S. Jo, and J.-Y. Hong, (2014), Projection of 21st century climate over Korean Peninsula: temperature and precipitation simulated by WRFV3.4 based on RCP4.5 and 8.5 scenarios, Atmosphere, 24, p541-554, (in Korean with English abstract). [https://doi.org/10.14191/Atmos.2014.24.4.541]
• Ahn, J.-B., J.-Y. Hong, and K.-M. Shim, (2016a), Agro-climate changes over Northeast Asia in RCP scenarios simulated by WRF, Int. J. Climatol., 36, p1278-1290. [https://doi.org/10.1002/joc.4423]
• Ahn, J.-B., and Coauthors , (2016b), Changes of precipitation extremes over South Korea projected by the 5 RCMs under RCP scenarios, Asia-Pacific J. Atmos. Sci., 52, p223-236. [https://doi.org/10.1007/s13143-016-0021-0]
• Bonan, G. B., (1998), The Land Surface Climatology of the NCAR Land Surface Model Coupled to the NCAR Community Climate Model, J. Climate, 11, p1307-1326. [https://doi.org/10.1175/1520-0442(1998)011<1307:tlscot>2.0.co;2]
• Chen, F., and J. Dudhia, (2001), Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part I: model implementation and sensitivity, Mon. Wea. Rev., 129, p569-585. [https://doi.org/10.1175/1520-0493(2001)129<0569:caalsh>2.0.co;2]
• Dudhia, J., (1989), Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model, J. Atmos. Sci., 46, p3077-3107. [https://doi.org/10.1175/1520-0469(1989)046<3077:nsocod>2.0.co;2]
• Hong, S.-Y., and M. Kanamitsu, (2014), Dynamical downscaling: Fundamental issues from an NWP point of view and recommendations, Asia-Pac. J. Atmos. Sci., 50, p83-104. [https://doi.org/10.1007/s13143-014-0029-2]
• Hong, S.-Y., J. Dudhia, and S.-H. Chen, (2004), A Revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation, Mon. Wea. Rev., 132, p103-120. [https://doi.org/10.1175/1520-0493(2004)132<0103:aratim>2.0.co;2]
• Hong, S.-Y., Y. Noh, and J. Dudhia, (2006), A new vertical diffusion package with an explicit treatment of entrainment processes, Mon. Wea. Rev., 134, p2318-2341. [https://doi.org/10.1175/mwr3199.1]
• Hur, J., and J.-B. Ahn, (2017), Assessment and prediction of the first-flowering dates for the major fruit trees in Korea using a multi-RCM ensemble, Int. J. Climatol., 37, p1603-1618. [https://doi.org/10.1002/joc.4800]
• Im, E.-S., J.-B. Ahn, A. R. Remedio, and W.-T. Kwon, (2008), Sensitivity of the regional climate of East/Southeast Asia to convective parameterizations in the RegCM3 modelling system. Part 1: Focus on the Korean peninsula, Int. J. Climatol., 28, p1861-1877. [https://doi.org/10.1002/joc.1664]
• Im, E.-S., J.-B. Ahn, and Jo, S.-R., (2015), Regional climate projection over South Korea simulated by the Had-GEM2-AO and WRF model chain under RCP emission scenarios, Clim. Res., 63, p249-266. [https://doi.org/10.3354/cr01292]
• Im, E.-S., Y.-W. Choi, and J.-B. Ahn, (2017), Worsening of heat stress due to global warming in South Korea based on multi-RCM ensemble projections, J. Geophys. Res., 122, p11444-11461. [https://doi.org/10.1002/2017JD026731]
• IPCC, (2014), Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of The Intergovernmental Panel on Climate Change, Stocker, T. F. et al. Eds., Cambridge University Press, p1535.
• Jung, M.-I., S.-W. Son, J. Choi, and Kang, H.-S., (2015), Assessment of 6-month lead prediction skill of the GloSea5 hindcast experiment, Atmosphere, 25, p323-337, (in Korean with English abstract). [https://doi.org/10.14191/Atmos.2015.25.2.323]
• Kain, J. S., (2004), The Kain-Fritsch convective parameterization: An update, J. Appl. Meteor. Climatol., 43, p170-181. [https://doi.org/10.1175/1520-0450(2004)043<0170:tkcpau>2.0.co;2]
• Kanamitsu, M., W. Ebisuzaki, J. Woollen, S.-K. Yang, J. J. Hnilo, M. Fiorino, and G. L. Potter, (2002), NCEP-DOE AMIP-II Reanalysis (R-2), Bull. Amer. Meteor. Soc., 83, p1631-1643.
• Kiehl, J. T., J. J. Hack, G. B. Bonan, B. A. Boville, B. P. Briegleb, D. L. Williamson, and P. J. Rasch, (1996), Description of the NCAR Community Climate Model (CCM3). NCAR Technical Note, p152.
• Kim, H. J., and J. B. Ahn, (2015), Improvement in prediction of the arctic oscillation with a realistic ocean initial condition in a CGCM, Climate Dyn., 28, p8951-8967. [https://doi.org/10.1175/JCLI-D-14-00457.1]
• Kim, M.-H., H.-S. Kang, Y.-H. Byun, S. Park, and W.-T. Kwon, (2011), Construction of the regional prediction system using a regional climate model and validation of its wintertime forecast, Atmosphere, 21, p17-33, (in Korean with English abstract).
• KMA, (2012), The Climate Atlas of Korea, Korea Meteorological Administration, p174, (in Korean).
• Lee, D.-K., D.-H. Cha, C.-S. Jin, and S.-J. Choi, (2013), A regional climate change simulation over East Asia, Asia-Pac. J. Atmos. Sci., 49, p655-664. [https://doi.org/10.1007/s13143-013-0058-2]
• Lee, D., and Coauthors , (2017), Thermodynamic and dynamic contributions to future changes in summer precipitation over Northeast Asia and Korea: a multi-RCM study, Climate Dyn., 49, p4121-4139. [https://doi.org/10.1007/s00382-017-3566-4]
• Lee, J.-W., and S.-Y. Hong, (2014), Potential for added value to downscaled climate extremes over Korea by increased resolution of a regional climate model, Theor. Appl. Climatol., 117, p667-677. [https://doi.org/10.1007/s00704-013-1034-6]
• Lee, J.-W., S.-Y. Hong, E.-C. Chang, M.-S. Suh, and H.-S. Kang, (2014), Assessment of future climate change over East Asia due to the RCP scenarios downscaled by GRIMs-RMP, Climate Dyn, 42, p733-747. [https://doi.org/10.1007/s00382-013-1841-6]
• Lee, S.-M., H.-S. Kang, Y.-H. Kim, Y.-H. Byun, and C. H. Cho, (2016), Verification and comparison of forecast skill between Global seasonal forecasting system version 5 and unified model during 2014, Atmosphere, 26, p59-72. [https://doi.org/10.14191/Atmos.2016.26.1.059]
• Lee, S.-S., J.-Y. Lee, K.-J. Ha, B. Wang, and J. K. E. Schemm, (2011), Deficiencies and possibilities for long-lead coupled climate prediction of the Western North Pacific-East Asian summer monsoon, Climate Dyn., 36, p1173-1188. [https://doi.org/10.1007/s00382-010-0832-0]
• MacLachlan, C., and Coauthors , (2015), Global Seasonal forecast system version 5 (GloSea5): a high-resolution seasonal forecast system, Quart. J. Roy. Meteor. Soc., 141, p1072-1084. [https://doi.org/10.1002/qj.2396]
• Meehl, G. A., and W. M. Washington, (1995), Cloud albedo feedback and the super greenhouse effect in a global coupled GCM, Climate Dyn., 11, p399-411. [https://doi.org/10.1007/s003820050083]
• Mlawer, E. J., S. J. Taubman, P. D. Brown, M. J. Iacono, and S. A. Clough, (1997), Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave, J. Geophys. Res., 102, p16663-16682. [https://doi.org/10.1029/97jd00237]
• Pacanowski, R. C., and S. M. Griffies, (2000), MOM 3.0 Manual, NOAA/Geophysical Fluid Dynamics Laboratory, Princeton, USA 08542, p708.
• Paulson, C. A., (1970), The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer, J. Appl. Meteor. Climatol., 9, p857-861. [https://doi.org/10.1175/1520-0450(1970)009<0857:tmrows>2.0.co;2]
• Ratnam, J. V., T. Doi, and S. K. Behera, (2017), Dynamical downscaling of SINTEX-F2v CGCM seasonal retrospective austral summer forecasts over Australia, J. Climate, 30, p3219-3235. [https://doi.org/10.1175/JCLI-D-16-0585.1]
• Skamarock, W. C., J. B. Klemp, J. Dudhia, D. O. Gill, D. M. Barker, M. G. Duda, X.-Y. Huang, W. Wang, and J. G. Powers, (2008), A description of the advanced research WRF version 3. NCAR Technical Note NCAR/TN-475+STR, p125.
• Sun, J., and J. B. Ahn, (2011), A GCM-based forecasting model for the landfall of tropical cyclones in China, Adv. Atmos. Sci., 28, p1049-1055. [https://doi.org/10.1007/s00376-011-0122-8]
• Sun, J., and J. B. Ahn, (2015), Dynamical seasonal predictability of the Arctic Oscillation using a CGCM, Int. J. Climatol., 35, p1342-1353. [https://doi.org/10.1002/joc.4060]
• Taylor, K. E., (2001), Summarizing multiple aspects of model performance in a single diagram, J. Geophys. Res., 106, p7183-7192. [https://doi.org/10.1029/2000jd900719]
• Wang, B., and Coauthors , (2009), Advance and prospectus of seasonal prediction: assessment of the APCC/Cli-PAS 14-model ensemble retrospective seasonal prediction (1980-2004), Climate Dyn., 33, p93-117. [https://doi.org/10.1007/s00382-008-0460-0]
• Wilks, D. S., (1995), Statistical Methods in the Atmospheric Sciences, Academic Press, p467.