
서울지역의 고해상도 수치표고모델기반 태양 에너지 산출
Abstract
Solar energy is calculated using high-resolution digital elevation model (DEM). In focus on Seoul metropolitan area, correction coefficients of direct and diffuse solar energy with the topographic effect are calculated from DEM with 1720, 900, 450, 90 and 30 spatial resolutions (m × m), respectively. The solar energy on the real surface with high-resolution is corrected using by the correction coefficients with topographic effect from the solar energy on horizontal surface with lower resolution. Consequently, the solar energy on the real surface is more detailed distribution than those of horizontal surface. In particular, the topographic effect in the winter is larger than summer because of larger solar zenith angle in winter. In Seoul metropolitan area, the monthly mean topographic effects are more than 200% in winter and within 40% in summer. And annual topographic effects are negative role with more than -60% and positive role with below 40%, respectively. As a result, topographic effect on real surface is not a negligible factor when calculating and analyzing solar energy using regional and global models.
Keywords:
Topographic effect, high resolution, digital elevation model, solar energy, Seoul1. 서 론
태양 에너지는 전지구적으로 지구대기를 순환시키는 근본적인 에너지원으로서 대기에 포함된 흡수기체와 에어러솔 및 구름에 의하여 흡수 또는 산란된다. 태양 에너지는 기후, 수문, 에너지, 건축, 산업, 농업 등의 다양한 연구에서 일차적인 에너지원으로 작용되거나 중요한 초기값으로 적용된다(Rogelj, 2013).
지상에 설치되어 태양 에너지를 관측하는 방법은 관리 및 보정 등이 매우 까다로우며 관측할 수 있는 영역이 제한적이기 때문에 넓은 영역에 대한 태양 에너지의 분포를 산출하기 위해서는 태양복사모델을 이용한다. 태양복사모델은 대기 중의 흡수기체와 구름에 의한 태양 에너지의 흡수 및 소산과정을 관측자료를 기반으로 모수화하여 계산하는 방법이다. 특히, 지표면에 도달되는 태양 에너지 분포는 태양광과 태양열 발전분야의 기초자료 활용된다(Zo et al., 2014). 이러한 방법은 대부분의 중규모 및 전지구 수치모델 등에서 적용되고 있으며 태양 에너지 발전을 위한 태양자원지도 개발에 적용되고 있다(Michael et al., 1978; George and Maxwell, 1999; Weymouth and Marshall, 1999; Perez et al., 2002; Lee and Park, 2008; Lee et al., 2011).
또한 복잡한 지형과 인공 구조물을 고려하여 지형효과를 적용하는 방법들이 적용되고 있다. 초기 penand-ink 방법 등을 이용하여 지형효과를 근사적으로 계산하였고(Hsia and Wang, 1985), 지리정보시스템(Geographic Information System, GIS) 기반으로 수치표고모델(Digital Elevation Model, DEM) 자료를 이용하여 지형의 고도(altitude), 경사각(slope) 그리고 경사면(aspect) 등을 산출하여 태양 에너지 분포에 미치는 지형효과의 영향에 대한 연구가 진행되었다(Dozier and Frew, 1990; Dubayah, 1994; Rich et al., 1994; Dubayah and Rich, 1995; Fu and Rich, 2000; Zo et al., 2014). 그러나 이들 연구들은 대체로 단순한 지형고도자료를 이용하여 분석이 수행되었으며 이상적인 지형을 고려하고 영역을 제한하여 실험하였기 때문에 실제 태양에너지 분포를 분석하는 것에는 한계가 있다.
따라서 본 연구에서는 서울의 고해상도 지형고도자료들을 이용하여 지형특성을 계산하였고 2013년 위성기반의 수평면 태양 에너지 계산과정에 적용하여 지형이 고려된 태양 에너지를 계산하였다. 그리고 수평면 태양 에너지 계산결과를 활용하여 지형고도자료의 해상도별 지형특성이 반영되었을 때 태양 에너지를 산출하여 지형효과를 분석하였다. 지형특성을 적용한 태양 에너지의 시·공간 분포를 계산하였고 연구기간(2013년) 동안 계산된 월 및 연 누적 태양 에너지를 이용하여 지형효과를 분석하였다.
2. 자료 및 방법
2.1 수치고도자료
지형효과를 계산하기 위하여 지형이 복잡하고 발달된 도시지역을 고려하여 서울을 중심으로 연구영역을 한정하였다. 서울은 다양한 지표특성이 나타나고 있고 특히 강과 산악, 상업지역과 공업지역 그리고 주거지가 포함된 도시이다. 서울 중심을 기준으로 동서로 한강이 흐르고 있으며 남과 북에 산악이 위치하고 있어 지형에 의한 차폐를 살펴볼 수 있다. 연구영역의 해상도별 지형고도자료는 Fig. 1과 같고 환경부와 미국 National Aeronautics and Space Administration (NASA)에서 제공되는 수치지도자료와 Shuttle Radar Topography Mission (SRTM, CGIAR-CSI, 2012) 자료(Digital Elevation Model, DEM)를 이용하였다. 원본 수치고도자료의 해상도는 10, 30, 90 m이고 이들 자료를 이용하여 1720, 900, 450, 90, 30 m 해상도로 면적 평균하여 지형고도자료를 구축하였으며(Jee and Choi, 2014; Park et al., 2015; Yi et al., 2015, 2016) 각각의 지형고도자료에 대한 정보는 Table 1에 정리하였다.
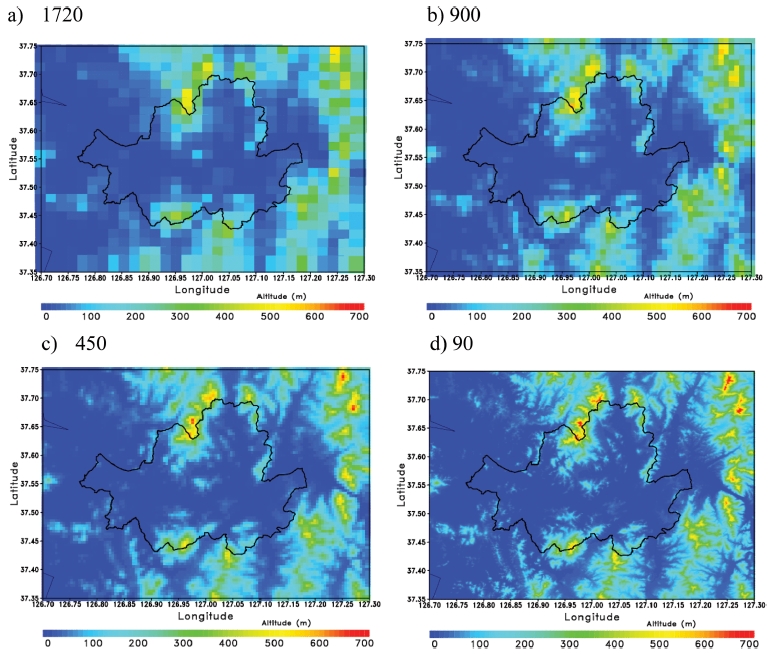
Geographic height from DEM (Digital Elevation Model) with spatial resolutions on Seoul area. 1720, 900, 450 and 90 represent spatial resolution with 1720, 900, 450 and 90 m, respectively.
2.2 수평면 태양 에너지
본 연구의 지형효과를 계산하고 분석하기 위한 초기자료는 한반도 전역에 대하여 수평면에서 계산되는 GWNU 태양 복사모델의 계산결과(Zo et al., 2016)를 활용하였다. GWNU 태양복사모델(Jee et al., 2011, 2013a, b)을 수행하기 위한 입력자료 중 기압과 수증기량(또는 가강수량) 등의 기상자료는 기상청 초단기 예측모델(Korean Local Analysis and Prediction System, KLAPS) 자료를 사용하였고 오존은 Ozone Monitoring Instrument (OMI) Level 3 TOMS product (OMTO3) 자료(일평균 및 월평균 자료)를 이용하였다. 그리고 에어러솔과 지표면 알베도는 Moderate resolution imaging spectrometer (MODIS; MOD08_D3 Level 3 aerosol optical depth, MCD43A3 Level 3 albedo) 자료(일 및 월평균 자료)를 적용하였다. 태양복사모델에서 가장 중요한 구름자료는 기상청에서 제공하고 있는 한반도영역의 Multi-Functional transport satellite-1R (MTSAT-1R) 위성자료를 이용하여 산출된 구름량을 이용하였다. 위성의 구름량은 태양의 천정각과 위성에서 관측된 가시채널의 알베도에 따른 감쇄효과로 정의하였다(Perez et al., 2002; Jee et al., 2011). 맑은 상태의 태양복사모델 계산값과 지상에서 관측된 태양 에너지를 기반으로 태양 천정각과 위성관측 알베도를 활용하여 다중 회귀식을 산출하였고 이를 이용하여 태양 에너지를 계산하기 위하여 직달과 산란성분으로 나누어 각각 적용하였다. 이상의 입력자료들을 이용하여 MTSAT-1R 위성자료의 해상도인 1720 m 해상도로 2013년에 대하여 매시간 태양 에너지를 계산하였다. Figure 2는 2013년 GWNU 태양 복사모델을 이용하여 산출된 서울중심의 수평면 태양 에너지의 분포이다. 대체로 고도가 높은 곳에서 높은 태양 에너지를 보였고 낮은 저지대 또는 해양에서 낮은 태양 에너지가 계산되었다. 특히 한강을 중심으로 낮은 태양 에너지의 분포를 보였다. Zo et al. (2016)에 따르면 지상관측자료를 이용하여 2013년 시간별 태양 에너지의 정확도를 계산하였을 때 결정계수 (r2)는 0.84이었고 평방근오차는 92.55W m-2를 보고하였다.
2.3 지형효과
2.1절에서 설명된 지형고도자료들을 이용하여 지형의 경사각, 경사면, 하늘시계요소(Sky View factor) 그리고 태양의 천정각(solar zenith angle)과 방위각(solar azimuth angle)별로 지형의 최대 그림자각을 계산하여 태양 에너지 계산에 적용하였다. 지형효과를 계산하는 알고리즘의 흐름도는 Fig. 3과 같다. 먼저, 지형고도자료를 이용하여 격자점에서의 경사각, 경사면을 계산한다. 그리고 격자점별 태양의 방위각(0~360o)에 대하여 최대고도를 찾아 그림자각을 산출한다. 산출된 경사각과 경사면 그리고 태양의 천정각을 이용하여 격자점에서의 경사면 하늘시계요소(χ)를 산출한다. 태양의 천정각과 태양의 방위각에 대한 차폐비율(κ(φo, θo))을 태양의 방위각과 천정각별로 산출한다. 본 연구에서는 태양의 방위각(0~355o)과 천정각(2.5~87.5o)에 대해서는 각각 매 5o마다 계산하여 1296면의 자료를 산출하여 적용하였다.
지형고도(DEM) 자료가 Fig. 4와 같이 지형고도의 격자점이 배치되었다고 가정하였을 때 격자점 5의 동서 및 남북방향의 기울기는 다음과 같다.
| (1) |
| (2) |
여기서 z은 격자의 고도이고 아래첨자들은 격자점의 위치이다. dx, dy는 동서 및 남북방향 격자점 사이의 거리로서 수치표고자료의 해상도에 해당되며 dz는 격자들의 고도차이이다.
식 (1)과 (2)에서 계산된 동서와 남북방향의 기울기를 이용하여 격자점 5의 경사각(β)과 경사면(φ)(북쪽으로부터의 시계방향 회전각)은 다음과 같다.
| (3) |
| (4) |
그리고 격자점에 도달하는 직달 태양 에너지는 식 (5)와 같이 계산된다.
| (5) |
여기서 Idirect는 수평면에 도달되는 직달 태양 에너지로 2.2절에서 계산된 값을 이용한다. θT는 태양 천정각과 계산 지점 경사면의 수선과 이루는 각으로서 식 (6)과 같다.
| (6) |
여기서 φo는 태양의 방위각(북쪽으로부터의 시계방향 회전각)을 의미한다(Kondratyev, 1969).
또한 계산 격자(거리는 xo이고 고도는 zo)로부터 φ 방향으로 xi 거리 만큼 떨어져 있는 지형의 고도가 zi라고 하면 직달 태양 에너지의 차폐각(shading angle, Hi(φ))은 다음 식과 같이 계산된다.
| (7) |
식 (5)와 (6)에서 θT > 90o는 계산하고자 하는 격자가 지형에 의하여 직달 태양 에너지가 차폐되는 것(self-shading)이고 θ0 > H(φ)는 계산하고자 하는 격자가 xi에 위치한 지형에 의하여 직달 태양 에너지가 차폐하는 되는 것(shading)이다. 따라서 계산하고자 하는 격자를 중심으로 영향을 미칠 수 있는 주변의 지형들을 조사하여 태양의 방위각과 태양의 천정각에 따라 재계산하는 과정이 필요하다. 본 연구에서는 영역내의 최고 지형고도를 기준으로 영향반경을 정하여 반복 수행하였다.
또한 격자점에 도달하는 산란 태양 에너지는 다음과 같이 계산된다.
| (8) |
여기서 Idiffuse는 2.2절에서 계산된 수평의 산란 태양 에너지이고 V는 하늘시계요소이며 주변 지형들이 산란 태양 에너지 계산에 미치는 영향을 0에서 1 사이의 값으로 나타낼 수 있으며 식 (9)로 계산된다.
| (9) |
하늘시계요소는 관측 격자점의 모든 방향에서 지형 등의 차폐물에 의하여 산란 태양 에너지가 차폐되지 않을 경우는 1이고 차폐가 많아질수록 0에 가깝게 계산된다. 이 식에서 γ1과 γ2는 경사면에서의 차폐각으로 계산되는 γ2는 π/2보다 클 수 없고, γ1은 0보다는 작을 수 없다.
| (10) |
여기서 H는 식 (7)에서 계산되는 태양 에너지의 차폐각이며 λ는 경사면에서의 차폐각을 의미하다. 계산지점의 지형 경사면의 방위각과 계산하고자 하는 태양의 방위각의 함수로 표현된다(Lai et al., 2009).
| (11) |
식 (5)와 식 (8)의 지형효과를 계산하기 위기하여 위하여 직달 태양 에너지와 산란 태양 에너지의 보정식(κ, χ)으로 나타낼 수 있다.
| (12) |
| (13) |
여기서 산란 태양 에너지의 보정계수(χ)는 계산하고자 하는 격자점에 의존적이며 직달 태양 에너지의 보정계수(κ)는 계산 격자점과 태양의 방위각(φo) 그리고 태양의 천정각(θ0)에 의존적임을 알 수 있다. 따라서 경사면에서의 직달 태양 에너지를 계산하기 위해서는 각 격자점 위치에서 태양의 천정각과 방위각에 따른 계산이 필수적이다. 본 연구에서 많은 계산을 최소화하기 위하여 격자점에서 영향을 미칠 수 있는 태양의 천정각과 방위각을 5o 간격으로 계산하여 적용하였다.
식 (5), (8), (12), (13)을 이용하여 계산된 직달과 산란 태양 에너지를 이용하여 지형효과가 적용된 전천 태양 에너지를 계산한다.
| (14) |
본 연구에서는 2.1절의 수치표고자료들을 이용하여 각 해상도별로 지형특성을 고려한 태양 에너지를 계산하였고 이들 결과들은 2.2절의 수평면에서의 태양 에너지와 비교하였다. 지형효과는 수평면에서의 태양 에너지에 대하여 실제지형의 태양 에너지의 비율로 정의하였다(TE = Bglobal/Iglobal). 지형효과는 경사면이 태양에 마주하는 면에서 최대값이 나타나고 반대쪽의 경사면에서 태양 에너지가 차폐되어 최소값이 나타난다. 이러한 지형효과의 계산은 월별 그리고 2013년(연구기간) 전체의 자료에 대하여 계산하여 분석하였다.
3. 결 과
3.1 지형효과
2.1절의 30 m 해상도의 지형고도자료를 이용하여 서울을 중심으로 지형고도, 경사각, 경사면 및 하늘시계요소는 Fig. 5와 같다. 서울을 중심으로 남, 북 그리고 동쪽에 600 m 이상의 산악이 위치하며 산악을 중심으로 지형의 경사각이 크게 나타나고 지형의 경사면이 복잡하게 나타난다. 하늘시계요소는 산악의 경사면에서 낮으며 평지에서는 대체로 1의 값을 갖는다.
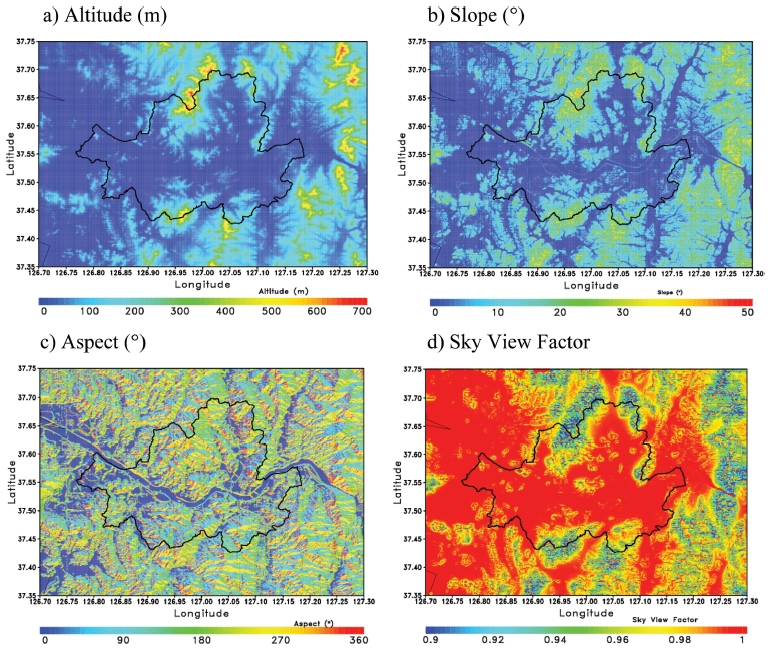
Altitude, slope, aspect and sky view factor calculated from DEM with spatial resolution with 30 m on Seoul.
Figure 5의 지형고도, 경사각, 경사면 및 하늘시계요소의 빈도분포를 Fig. 6에 나타내었다. 지형고도는 대체로 낮은 고도에 집중되었고 0 m에 해당되는 강과 바다의 비율은 3% 이하였으며 600 m 이상의 고도는 1% 이하였다. 경사각은 지형고도와 유사하게 낮은 경사각이 많이 나타났으며 평평한 지형이 20% 이하였고 35o 이상의 심한 경사각은 1% 이하였다. 경사면은 전체방위각에 대하여 고르게 분포하였으나 경사면 없이 평평한 지형이 20% 이상으로 다수 분포되었다. 하늘시계요소의 75% 이상은 0.975 이상으로 산란 태양 에너지에 대한 차폐가 거의 없으며 산란 태양 에너지의 10% 이상 차폐가 발생되는 0.85 이하의 하늘시계요소가 2% 이하로 분포되었다.
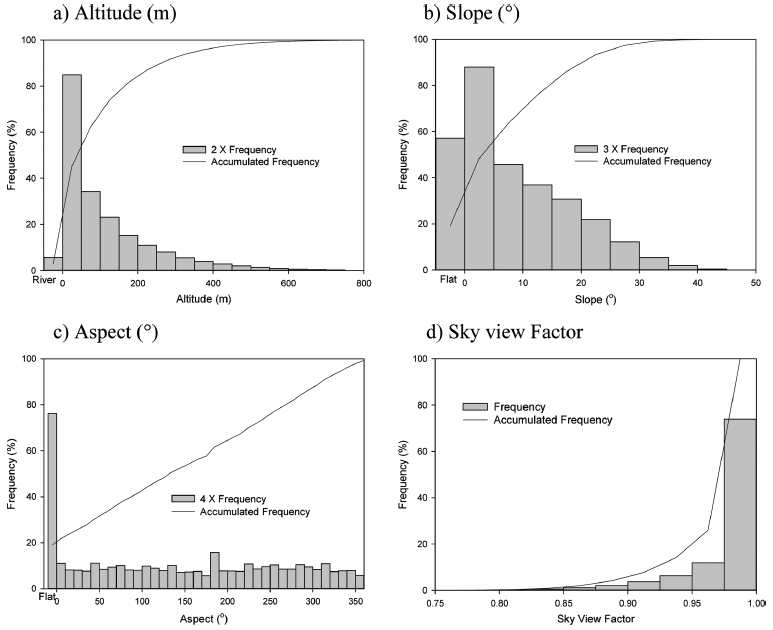
Frequency and Accumulated frequency of altitude, slope, aspect and sky view factor calculated from DEM with spatial resolution with 30 m on Seoul and surrounding area.
지형의 경사각과 경사면에 따라 지형에 의한 그림자각은 태양의 방위(0o~359o) 1o 간격으로 계산하였다. Figure 7은 태양의 방위각을 0, 90, 180, 270o를 기준으로 최대 그림자각을 나타낸 것이다. 고도가 높은 지형과 가까이 위치할수록 그림자각은 크다. 즉, 높은 지형의 주변에서는 태양의 고도가 높아야만 태양 에너지가 직접 도달하게 된다. 그림에서 최대 그림자 각은 약 42o였고 지형이 위치한 곳에서 태양방위각을 따라 멀어질수록 최대 그림자각은 줄어든다.
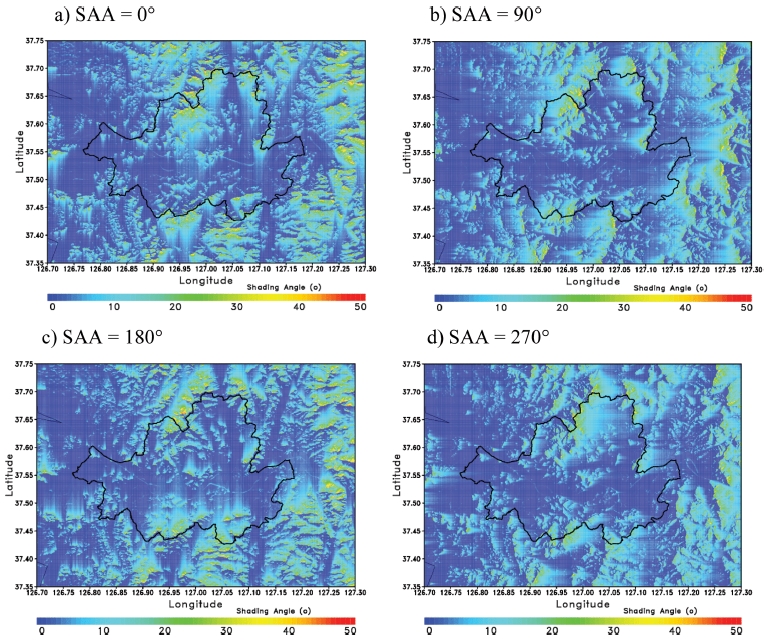
The distribution of maximum shading angle on surface calculated from DEM with spatial resolution with 30 m for solar azimuth angle with 0, 90, 180 and 270o, respectively.
지형의 경사각, 경사면, 하늘시계요소 그리고 태양의 방위각에 따른 최대 그림자각을 이용하여 식 (5)의 직달 태양 에너지를 계산하기 위한 보정계수(κ)를 계산하였다. 직달 태양 에너지의 보정을 위한 보정계수는 태양의 천정각과 태양의 방위각을 5o 단위로 분류하여 계산하였다. 천정각은 2.5o~87.5o에 대하여 5o 간격으로 18개 그리고 태양 방위각은 0o~355o에 대하여 5o 간격으로 72개의 각에 대하여 계산하여 최종 1296개의 면으로 구성된 자료를 계산하였다. Figure 8은 천정각이 72.5o이고 태양의 방위각이 0, 90, 180, 270o 일때의 보정계수를 나타낸 것이다. 태양의 방위각이 90o일 때는 일출 근처라고 볼 수 있고 이때 지형의 동쪽 경사면은 직달 태양 에너지가 직접적으로 도달되고 반대면은 직달 태양 에너지가 지형에 의하여 차폐되는 것을 알 수 있다. 반대로 태양의 방위각이 270o일 때는 일몰 근처라고 볼 수 있고 태양의 방위각이 90o 일 때와는 반대로 태양 에너지가 서쪽 경사면에 도달된다.
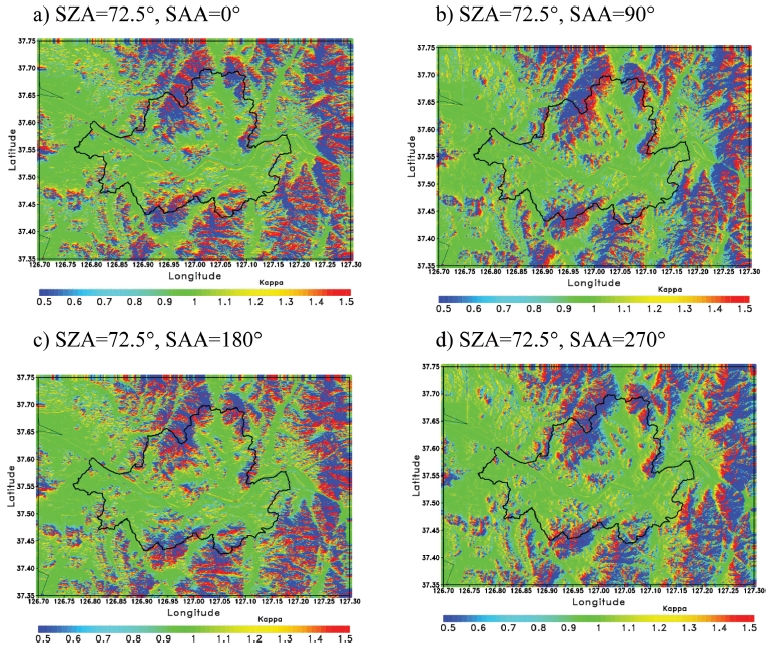
Correction coefficient (κ) for direct solar radiation on surface calculated from DEM with spatial resolution with 30 m. SZA and SAA represent solar zenith angle and solar azimuth angle, respectively.
식 (8)의 산란 태양 에너지는 지형고도자료에서 계산된 하늘시계요소와 지형의 경사각을 이용하여 계산할 수 있다. Figure 9는 해상도별 지형고도와 지형의 경사각을 이용하여 계산된 산란 태양 에너지의 보정계수(χ)이다. 대체로 지형의 경사면에서 하늘시계요소는 1 이하의 값을 보이며 지형고도자료의 해상도 증가에 따라 주변 지형과 고도차가 발생되어 작은 보정계수가 나타나며 고해상도의 보정계수를 저해상도 영역에 대하여 평균하였을 때 저해상도의 보정계수와 유사한 분포가 나타난다.
3.2 지표면의 태양 에너지
3.1절에서 계산된 직달 및 산란 태양 에너지의 보정계수를 2.2절에서 계산된 수평면의 태양 에너지 결과에 적용하여 지형특성이 고려된 지표면에서의 태양 에너지를 계산하였다. 매시간 계산되는 1720 m 해상도의 수평면 직달, 산란 및 전천 태양 에너지를 해당 격자로 내삽한 후 지형특성을 적용하여 태양 에너지를 산출한다. Figure 10은 30 m 해상도의 수치고도모델 자료를 적용하여 2013년 6월 22일과 12월 22일의 시간별 전천 태양 에너지의 분포이다. 그림과 같이 일출과 일몰시 태양 에너지는 작고 정오에 가까울수록 태양 에너지는 증가된다. 지형에 의하여 차폐 또는 산란되어 그림자 부분에서 값이 작아지며 태양을 직접적으로 받는 경사면에서의 태양 에너지는 증가되었다. 여름철 일출과 일몰시간이 겨울철보다 빠르고 느리기 때문에 동일시각(07, 08, 09, 17, 18, 19 LST)의 겨울철 태양 에너지는 0으로 분포된다. 또한, 천정각이 낮은 겨울철에 지형에 의한 차폐가 크게 나타나 지형효과 크게 나타난다.
매시간 계산된 태양 에너지는 월별 그리고 1년 동안 누적하여 지형효과를 고려한 태양 에너지, 수평면의 태양 에너지 그리고 이들의 차이를 해상도별로 Fig. 11에 나타내었다. 산출된 태양 에너지는 직달, 산란, 전천으로 분류하여 계산되었으며 지형에 의하여 지표면에 도달하는 태양 에너지는 고해상도에서 더욱 뚜렷이 나타나며 세밀하게 표현되었다.
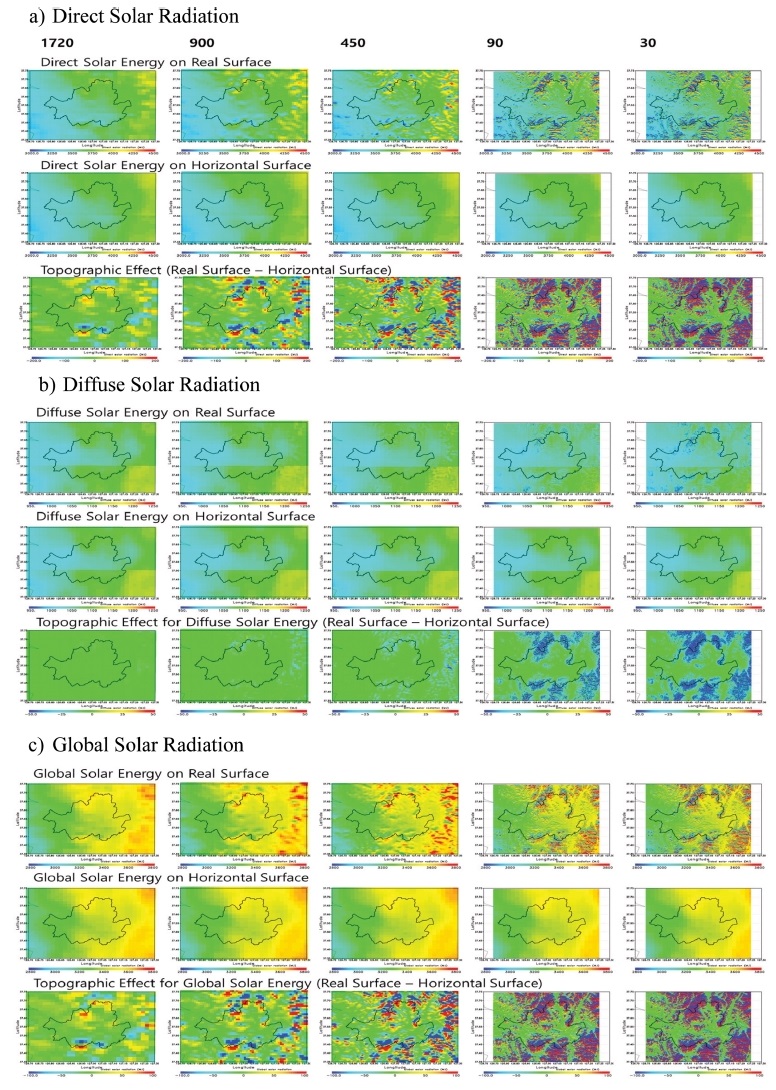
Direct, diffuse and global solar radiations on horizontal and real surface by DEMs with spatial resolutions in 2013 and these differences.
지형면에서의 월누적 전천 태양 에너지와 수평면 전천 태양 에너지를 비교하여 지형효과를 계산하였다(Fig. 12). 지형효과는 지형면의 태양 에너지를 기준으로 수평면 태양 에너지의 비율을 이용하여 계산하였다. 천정각이 큰 겨울철을 중심으로 효과가 50% 이상으로 크게 나타났으며 여름철의 지형효과는 30% 이하로 상대적으로 낮게 나타났다. 해상도가 높은 자료일수록 지형효과는 크게 나타났으며 월별 지형효과도 급격하게 변화하였다. 900 m 해상도 이하의 자료를 이용하였을 때 지형효과는 월별 10% 이내였고 월별 차이는 고해상도 자료와 비교하여 작은 것으로 분석되었다.
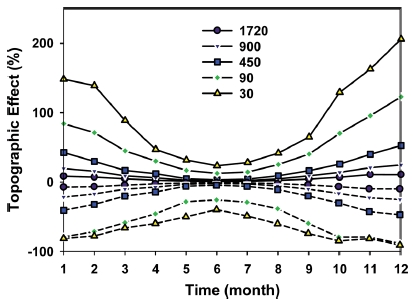
Monthly topographical effect (%) from maximum and minimum solar radiation difference between real and horizontal surface with spatial resolutions.
Figure 13은 연누적 태양 에너지 계산 결과를 이용하여 지형효과를 분석하였다. 추가로 연평균 구름량, 직달과 산란 태양 에너지의 지형효과 적용을 위한 보정계수를 비교하였다. 구름량은 수평면 태양 에너지를 계산하기 위한 입력자료이므로 차이는 미미하였다. 지형효과 적용을 위한 보정계수의 경우 직달 태양 에너지의 경우 해상도에 따라 0.988부터 0.922로 수평면 태양 에너지를 대체로 감소시키는 역할로 분석되었다. 이러한 결과는 연구영역 내 지형의 구성이 남향 경사면보다 북향 경사면이 더 넓게 분포된다고 유추할 수 있다. 또한 산란 태양 에너지의 보정계수는 해상도에 따라 0.998에서 0.983로 직달 태양 에너지의 보정계수와 비교하여 상대적으로 감소율이 작았다. 지형효과의 보정계수는 대체로 감소하는 역할이 지배적이었고 해상도가 높아질수록 감소율은 증가되었다.
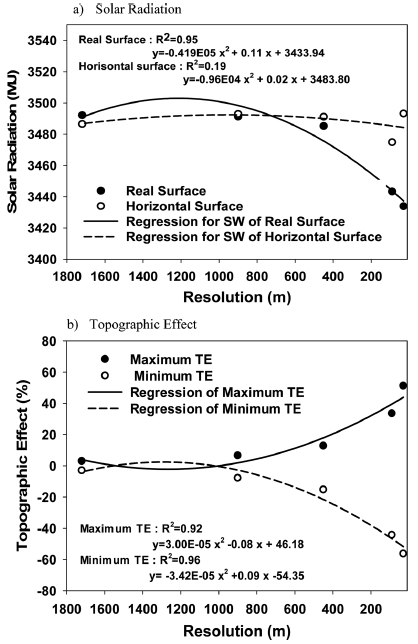
Solar radiation and topographic effect with spatial resolutions. Solar radiations are calculated on the real and horizontal surfaces. Topographic effect calculated by ratio of solar radiation between real and horizontal surface.
직달 태양 에너지는 해상도가 높아질수록 지형고도의 상세화로 분포가 복잡하게 나타나며 높은 지형 주변에서 수평면에 도달하는 태양 에너지와 비교하여 지형의 차폐 또는 경사면에 직접 도달 등의 이유로 수평면보다 ± 50% 이상의 차이를 보였다. 반면 산란 태양 에너지의 차이는 하늘시계요소의 분포와 유사하게 산악의 계곡 또는 산악의 주변에서 뚜렷이 발생되었다. 특히 고해상도의 지형자료를 이용하였을 때 산악의 계곡에서 차이가 있었고 대체로 태양 에너지가 감소시키는 역할을 보였으며 산악의 정상부 등에서는 상승의 역할을 보였다. 산란 태양 에너지에서 지형의 효과는 ± 30% 이상으로 나타났다. 이상과 같이 지표면에 도달하는 태양 에너지는 직달 태양 에너지에 의존성을 가지며 직달 태양 에너지와 유사한 편차를 나타내었다. 직달 태양 에너지와 마찬가지로 ± 50% 이상의 지형효과가 나타났다(Table 2).

Summary of parameters on the real and horizontal surface with DEM resolutions. Parameters are include cloud fraction, correction coefficients, direct, diffuse and global solar radiation.
해상도별 태양 에너지의 분포는 해상도와 결정계수(R2)가 지형면에서 0.95로 해상도에 밀접한 영향을 미치는 것으로 분석되고 수평면에서의 태양 에너지는 해상도와는 별개로 나타나는 것으로 분석된다(R2 = 0.17). 1720 m 해상도의 태양 에너지는 지형효과가 양의 효과가 있었고 900 m 해상도 이상의 지형자료를 사용하였을 때부터 음의 역할을 보였다. 이러한 이유로는 초기 수평면 태양 에너지 계산에 있어서 대부분의 복사모델 입력자료들이 저해상도의 자료이고 특히 구름의 경우 1720 m 해상도로 입력되기 때문에 구름영역 외에서 나타나는 지형효과가 상대적으로 태양 에너지 증가에 기여한 것으로 분석된다. 그리고 1 km 이상의 고해상도 에서는 지형효과가 강화되어 상대적으로 태양 에너지를 감소하는 것으로 분석되었고 연구영역 내의 북향의 경사면이 남향의 경사면보다 넓게 분포한 것으로 사료된다. 연누적 태양 에너지에 대한 지형효과는 1720 m 일 때 ± 5% 이내이었으나 30 m 일 때 ± 60% 이상으로 월별 지형효과보다는 낮게 나타나고 있으며 해상도 증가에 따라 급격히 증가되었다.
4. 결 론
서울의 고해상도 지형고도자료를 이용하여 지형효과가 반영된 태양 에너지를 산출하였다. 먼저 지형고도자료를 이용하여 지형의 경사각, 경사면과 하늘시계요소 등의 지형특성을 산출하였다. 산출된 지형특성 결과를 이용하여 수평면에 도달하는 태양 에너지를 직달과 산란 태양 에너지로 분류하여 각각을 보정하는 보정계수를 산출하여 지형이 고려된 태양 에너지를 산출하였다. 직달과 산란 태양 에너지의 보정을 위한 보정계수는 지형면에서의 태양의 천정각과 방위각을 고려하여 산출할 수 있다. 직달 태양 에너지는 지형의 차폐 또는 그림자 효과를 통하여 보정할 수 있고 산란 태양 에너지는 주변지형에 의한 차폐율을 고려하여 하늘시계요소를 지형의 경사각을 적용하여 계산하였다.
서울 중심으로 1720, 900, 450, 90, 30 m 해상도의 지형고도자료를 이용하여 지형특성을 계산하였다. 지형고도자료의 해상도에 따라 계산된 직달 및 산란 태양 에너지의 보정계수는 고해상도의 지형고도자료를 적용할수록 상세한 계산이 되었다. 이는 지형고도자료의 상세한 표현으로 주변 지형에 의한 태양 에너지의 차폐 및 그림자 효과가 뚜렷이 나타나는 것으로 2013년 6월 22일과 12월 22일에 적용하여 태양 에너지를 산출하였을 때 일출 후와 일몰 전에 뚜렷한 효과가 나타난다. 특히, 겨울철 태양의 고도각이 낮아 여름철 보다 더울 뚜렷한 효과를 나타낸다. 월별 태양 에너지의 누적을 살펴보았을 때 해상도에 따른 지형효과의 차이는 겨울철의 경우 200% 이상 나타났고 여름철의 경우에는 40% 이내로 나타났다. 지형효과의 보정계수를 분석하였을 때 대체로 직달과 산란 태양 에너지를 감소시키는 역할을 하였고 산란 태양 에너지보다 직달 태양 에너지의 경우에 계산지점의 위치와 태양의 위치에 따라 그 차이가 뚜렷이 나타났다. 또한 해상도 증가에 따라 이러한 보정계수의 역할은 증가되는 것으로 분석되었다.
연 누적 태양 에너지를 통하여 전체적인 지형효과를 산출하였을 때 지형효과는 수평면의 태양 에너지와 비교하여 감소시키는 역할을 하였다. 이는 지형효과를 계산한 결과에서도 나타나고 있으며 양의 편차(최대 +50%)보다는 음의 편차(-60%)가 다소 우세하게 나타났다. 즉, 서울을 포함한 영역에서 지형을 고려하였을 때 위치에 따라 태양 에너지의 차폐 또는 그림자 효과로 인하여 태양 에너지를 감소할 수 있음을 의미한다.
이상의 결과를 보았을 때, 기존의 태양 에너지 자원 지도 등 태양 에너지 연구들은 수평면에서의 태양 에너지를 대체로 분석하였다. 그러나 고해상도 지형고도자료를 이용하여 지표면에 도달하는 태양 에너지를 분석하였을 때 지형효과는 무시할 수 있는 수준이 아니다. 지형에 의한 태양 에너지의 차폐는 지형고도자료의 해상도 증가에 따라 중요성이 높아진다. 특히, 건물 등 인공구조물이 복잡하게 위치한 도시에서의 태양 에너지 분석을 위해서는 정확한 고해상도 지형고도자료뿐만 아니라 정확한 건물 등 자료구축이 선행되어야 한다.
Acknowledgments
본 연구는 기상청 차세대도시농림융합스마트기상서비스개발(WISE) 사업의 지원으로 수행되었습니다(KMIPA-2012-0001-1). 기상청 슈퍼컴퓨터가 활용되도록 지원해준 기상청 관측기반국 국가기상슈퍼컴퓨터센터에 특별히 감사 드립니다.
References
- CGIAR-CSI, (2012), SRTM 90m Digital Elevation Data, [Available online at http://srtm.csi.cgiar.org/index.asp].
- Dozier, J., and J. Frew, (1990), Rapid calculation of terrain parameters for radiation modeling from digital elevation data. IEEE Trans, Geosci. Remote Sens, 28, p963-969.
-
Dubayah, R. C., (1994), Modelling a solar radiation topoclimatology for the Rio Grande River Basin, J. Veg. Sci, 5, p627-640.
[https://doi.org/10.2307/3235879]

-
Dubayah, R. C., and P. M. Rich, (1995), Topographic solar radiation models for GIS, Int. J. Geogr. Inf. Syst, 9, p405-419.
[https://doi.org/10.1080/02693799508902046]

- Fu, P., and P. M. Rich, (2000), The Solar Analyst 1.0 User Manual, Helios Environment Modeling Institute, p49.
- George, R. L., and E. L. Maxwell, (1999), High-resolution maps of solar collector performance using a climatological solar radiation model, Proc. of the 1999 Annual Conference, American Solar Energy Society, p243-248.
- Hsia, Y. J., and W. Wang, (1985), Calculation of Potential Solar Irradiance on Slopes, Taiwan Forestry Research Institute, Research Note 001, p22.
-
Jee, J. B., I. Zo, C. Lee, Y. Choi, K. Kim, and K. T. Lee, (2013a), Analysis of very high resolution solar energy based on solar-meteorological resources map with 1km spatial resolution, J. Korean Soc. New Renewable Energy, 9, p15-22, (in Korean with English abstract).
[https://doi.org/10.7849/ksnre.2013.9.2.015]

-
Jee, J. B., I. Zo, and K. T. Lee, (2013b), A study on the retrievals of downward solar radiation at the surface based on the observations from multiple geostationary satellites. Korean, J. Remote. Sens, 29, p123-135, (in Korean with English abstract).
[https://doi.org/10.7780/kjrs.2013.29.1.12]

- Jee, J. B., W.-H. Lee, I.-S. Zo, and K.-T. Lee, (2011), Correction of one-layer solar radiation model by multi-layer line-by-line solar radiation model, Atmosphere, 21, p151-162, (in Korean with English abstract).
-
Jee, J. B., and Y.-J. Choi, (2014), Conjugation of landsat data for analysis of the land surface properties in capital area, J. Korean Earth Sci. Soc, 35, p54-68, (in Korean with English abstract).
[https://doi.org/10.5467/JKESS.2014.35.1.54]

- Kondratyev, J., (1969), Radiation in the Atmospheric, Academic Press, USA, p916.
-
Lee, S.-H., S.-W. Kim, W. M. Angevine, L. Bianco, S. A. McKeen, C. J. Senff, M. Trainer, S. C. Tucker, and R. J. Zamora, (2011), Evaluation of urban surface parameterizations in the WRF model using measurements during the Texas Air Quality Study 2006 field campaign, Atmos. Chem. Phys, 11, p2127-2143.
[https://doi.org/10.5194/acp-11-2127-2011]

- Lee, S.-H., and S.-U. Park, (2008), A vegetated urban canopy model for meteorological and environmental modelling, Bound.-Layer Meteor.t, 126, p73-102.
-
Lai, Y.-J., M.-D. Chou, and P.-H. Lin, (2009), Parameterization of topographic effect on surface solar radiation, J. Geophy. Res, 115, D01104.
[https://doi.org/10.1029/2009JD012305]

- Michael, K., U. Pilz, and E. Raschke, (1978), A modified two-stream approximation for computations of the solar radiation budget in a cloudy atmosphere, Tellus, 30, p429-435.
-
Park, S. H., J. B. Jee, and C. Y. Yi, (2015), Sensitivity test of the numerical simulation with high resolution topographies and landuses over Seoul metropolitan areas, Atmosphere, 25, p323-336, (in Korean with English abstract).
[https://doi.org/10.14191/Atmos.2015.25.2.309]

-
Perez, R., P. Ineichen, K. Moore, M. Kmiecik, C. Chain, R. George, and F. Vignola, (2002), A new operational model for satellite-derived irradiances: Description and validation, Sol. Energy, 73, p307-317.
[https://doi.org/10.1016/s0038-092x(02)00122-6]

- Rich, P. M., W. A. Hetrick, S. C. Saving, and R. O. Dubayah, (1994), Using viewshed models to calculate intercepted solar radiation: Applications in ecology, ASPRS Technical papers, p524-529.
- Rogelj, J., (2013), Summary for policymakers, Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to The Fifth Assessment Report of The Intergovernmental Panel on Climate Change, T. F. Stocker et al. Eds., Cambridge University Press, Cambridge, p3-29.
- Weymouth, G. T., and J. F. Le Marshall, (1999), An operational system to estimate global solar exposure over the Australian region from satellite observation, Australia Meteor. Mag, 48, p181-195.
-
Yi, C., S. M. An, K. R. Kim, H.-G. Kwon, and J.-S. Min, (2016), Surface micro-climate analysis based on urban morphological characteristics: Temperature deviation estimation and evaluation, Atmosphere, 26, p445-459, (in Korean with English abstract).
[https://doi.org/10.14191/Atmos.2016.26.3.445]

-
Yi, C., T. H. Kwon, M.-S. Park, Y. J. Choi, and S. M. An, (2015), A study on the roughness length spatial distribution in relation to the Seoul building morphology, Atmosphere, 25, p339-351, (in Korean with English abstract).
[https://doi.org/10.14191/Atmos.2015.25.2.339]

-
Zo, I.-S., J.-B. Jee, and K.-T. Lee, (2014), Development of GWNU (Gangneung-Wonju National University) onelayer transfer model for calculation of solar radiation distribution of the Korean peninsula, Asia-Pac. J. Atmos. Sci, 50, p575-584.
[https://doi.org/10.1007/s13143-014-0047-0]

-
Zo, I.-S., J.-B. Jee, K.-T. Lee, and B.-Y. Kim, (2016), Analysis of solar radiation on the surface estimated from GWNU solar radiation model with temporal resolution of satellite cloud fraction, Asia-Pac. J. Atmos. Sci, 52, p405-412.
[https://doi.org/10.1007/s13143-016-0024-x]





