안전한 항공기 운항을 위한 현업 전지구예보모델 기반 깊은 대류 예측 지수: Part 1. 개발 및 통계적 검증
Abstract
Deep convection can make adverse effects on safe and efficient aviation operations by causing various weather hazards such as convectively-induced turbulence, icing, lightning, and downburst. To prevent such damage, it is necessary to accurately predict spatiotemporal distribution of deep convective area near the airport and airspace. This study developed a new index, the Aviation Convective Index (ACI), for deep convection, using the operational global Unified Model of the Korea Meteorological Administration. The ACI was computed from combination of three different variables: 3-hour maximum of Convective Available Potential Energy, averaged Outgoing Longwave Radiation, and accumulative precipitation using the fuzzy logic algorithm. In this algorithm, the individual membership function was newly developed following the cumulative distribution function for each variable in Korean Peninsula. This index was validated and optimized by using the 1-yr period of radar mosaic data. According to the Receiver Operating Characteristics curve (AUC) and True Skill Score (TSS), the yearly optimized ACI (ACIYrOpt) based on the optimal weighting coefficients for 1-yr period shows a better skill than the no optimized one (ACINoOpt) with the uniform weights. In all forecast time from 6-hour to 48-hour, the AUC and TSS value of ACIYrOpt were higher than those of ACINoOpt, showing the improvement of averaged value of AUC and TSS by 1.67% and 4.20%, respectively.
Keywords:
Deep convection, Aviation Convective Index (ACI), Optimization, Receiver Operating Characteristics (ROC) curve analysis1. 서 론
대류 현상은 전선과 지형에 의한 강제 상승, 수증기 유입으로 인한 비단열 과정, 그리고 불안정도 해소와 같은 다양한 기상학적 요인들로 인해 발생하는 상승 기류를 의미한다. 그 중 높은 고도까지 발달하는 깊은 대류는 난류, 착빙, 그리고 낙뢰와 같은 다양한 재해 기상을 유발하기 때문에 안전한 항공기 운항을 위해서는 깊은 대류에 대한 시공간 예측은 필수적이다.
미국과 유럽에서는 항공기 운항에 있어서 예보자의 적절한 의사 결정을 돕기 위해, 전지구 영역에서 발생하는 깊은 대류의 분포 및 강도를 예측하는 연구들이 활발히 진행되어 왔다. 국제 민간 항공 기구(International Civil Aviation Organization, 이하 ICAO)에서는 내륙뿐만 아니라 해양성, 그리고 대륙 간의 대류를 예측하기 위해 World Area Forecast System(WAFS) Cumulonimbus (Cb)를 개발하였다(ICAO, 2012). 영국(WAFS-London)과 미국(WAFS-Washington)의 통합 모델(Unified Model, 이하 UM)과 전 지구 예측 시스템(Global Forecast System) 모델을 기반으로 6시간마다 4000 ft min-1 또는 1220 m min-1 이상의 강한 상승 대류의 수평 발생 분포, 운정 고도, 운저 고도에 대한 예측 결과를 산출한다. 먼저, WAFS Cb의 발생 유무는 특정 임계 값을 기준으로 각각의 수치 모델에서 생산되는 대류성 강수량에 따라 결정되며, Cb가 존재한다고 판단되는 경우에는 특정 격자에서 예측된 운량에 따라 0부터 1까지의 무차원 값으로 할당된다. 이처럼 WA FS C b는 특정 단일 수치예보모델의 결과를 기반으로 전지구 규모의 강한 대류에 대한 결정론적 예측 결과를 제공한다.
뿐만 아니라 미국 국립대기연구센터(National Center for Atmospheric Research, 이하 NCAR)에서는 2개 이상의 앙상블 수치모델 결과를 사용하여 다중모델 앙상블 기반 확률 예측 시스템인 Ensemble Prediction of Oceanic Convective Hazards (EPOCH)을 개발하였다(Melling et al., 2019). 6시간마다 제공되는 Global Ensemble Forecast System (GEFS)와 Canadian Meteorological Center Ensemble (CMCE)의 예측장을 사용하여 30,000 피트 고도 이상 발달하는 강한 대류에 대한 발생 확률을 산출한다. WAFS Cb와 마찬가지로 EPOCH은 전구 영역에서 대류 예측 결과를 제공하기 때문에 해양 또는 대륙 간에 발생하는 대류 예보에 용이하다.
앞서 언급한 종래 기술들은 몇 가지 한계점이 존재한다. WAFS Cb와 EPOCH은 내륙뿐만 아니라 해양 및 대륙 사이에 발생하는 대류를 예측하는 데 활용되고 있지만, 두 시스템의 수평 해상도는 각각 1.25o와 1o로 매우 성기다는 단점이 있다. 이러한 수평해상도는 종관 규모 미만의 현상을 예측하는 데 한계가 있을 수 있다. 또한 WAFS Cb의 경우, 오직 수치모델에서 계산된 운량만을 사용하여 깊은 대류에 대한 예측장을 산출한다. 하지만 전지구예보모델에서 생산되는 단일 변수의 예측 결과는 대류의 발달 과정을 충분히 설명하지 못한다. 이러한 한계는 고해상도 모델 기반 지역 규모 예측 시스템에도 여전히 존재한다. 현대에 들어서는 컴퓨터 계산 자원의 증가로 고해상도 지역 규모 수치 모델, 특별히, 적운 모수화 방안을 사용하지 않아도 격자 규모에서 깊은 대류의 발달이 명시적으로 모의되는 모델(Convection-Allowing Models, CAMs)이 깊은 대류와 관련된 우박과 토네이도와 같은 중규모 재해 기상을 예측하는 기술에 활발하게 활용되고 있다(Sobash et al., 2016; Wendt et al., 2016; Gagne et al., 2017). CAMs를 활용한 대부분의 연구에서도 마찬가지로 단일 변수의 한계점을 극복하기 위해 상승 속도와 수직 와도를 동시에 고려한 Updraft Helicity (UH)와 같은 대변 인자 및 지수를 사용하고 있다(Sobash et al., 2011; Clark et al., 2012; Wendt et al., 2016, Jahn et al., 2022). 이처럼 대류의 발달 과정을 보다 정확히 예측하기 위해서는 대류의 물리적인 특성과 관련 깊은 여러 변수들이 함께 고려되어야 한다.
깊은 대류는 발달하는 과정에서 특정 지역이 갖는 지역적 특성이 반영된다. 한반도는 대부분 복잡한 산악 지형으로 이루어져 있기 때문에 지형적 강제력이 대류가 촉발하는 것을 도울 수 있다. 또한, 여름철에는 북태평양 고기압의 세력이 한반도까지 확장되어, 많은 양의 수증기와 고온의 공기가 유입되는 고기압 가장자리 전면에서는 전선 및 대류 발생의 호조건이 조성된다. 즉, 이러한 한반도 고유의 기상학적 특성을 고려하여 한반도 주변에서 발생하는 깊은 대류를 정확히 예측하기 위해서는 한반도 지역을 중심으로 개발되어 지역적인 특성이 고려될 필요가 있다. 하지만 현재 국내에는 자국 수치모델을 기반으로 개발된 깊은 대류 예측 시스템이 없는 실정이다. 국내 공항, 그리고 동아시아를 포함한 넓은 공역을 중심으로 향후 일관적인 예보 지원을 위해서는 국내 전지구 예보모델을 기반으로 예측 시스템이 개발되어야 한다.
본 연구에서는 국내 공항 및 넓은 공역 지역에 대한 깊은 대류 예측을 위해 우리나라에 적합한 새로운 예측 지수인 Aviation Convective Index(이하 ACI)를 개발하였다. 해당 지수는 앞서 언급된 선행 연구에서 사용된 전지구 모델보다 더욱 고해상도의 기상청 현업 전지구 예보모델을 기반으로 개발되었으며, 국내 관측 자료를 통해 검증되었다. 지수를 계산하는데 사용된 결합 알고리즘은 특정 지역에 최적화 시킬 수 있다는 장점이 있다. 본 연구에서는 한반도 지역을 중심으로 지수의 예측 성능을 향상시켰다. 해당 연구는 파트 1과 파트 2로 나뉘어져 있으며, 본 논문인 파트 1에서는 ACI를 개발하는 데 사용한 자료와 방법론, 그리고 장기간에 대한 최적화 및 통계적 검증을 담고 있다. 파트 2에서는 ACI 지수의 계절별 최적화, 통계적 검증, 사례 분석을 통한 정성적 검증 내용을 다루고 있다.
2. 자료 및 방법론
2.1 입력 및 검증 자료
국내 공항 및 공역 예보에 활용 가능한 현업 예보모델에는 전지구 예보모델(Global Data Assimilation and Prediction System, 이하 GDA PS)과 전지구 앙상블예보모델(Ensemble Prediction System for Global, 이하 EPSG)이 있다. 하지만 EPSG 자료는 32 km의 낮은 수평 해상도로 이루어져 있기 때문에 대류 현상을 충분히 예측하기에는 한계가 있다. 반면에 GDAPS의 경우, 더 높은 수평 해상도의 자료를 제공한다. 통합모델(Unified Model) 기반의 G DA PS(이하 UMGDAPS) 자료의 수평 해상도는 10 km이며, 한국형 수치모델(Korean Integrated Model) 기반 GDAPS 자료는 12 km의 수평 격자를 지니고 있다. 본 연구에서는 현업 전지구 예보모델 중 가장 해상도가 높은 UM-GDAPS 예측장을 입력자료로 사용하였다. Table 1은 UM-GDAPS에 대한 정보를 보여준다. 해당 예보 모델은 하루에 4회(0000, 0600, 1200, 1800 UTC) 예측이 수행되며, 288시간까지 6시간마다 예측장을 제공한다. 본 연구에서는 2021년, 1년 기간 동안의 6시간부터 48시간까지의 예측장을 사용하여 ACI를 개발하였다.

Model Information of Global Data Assimilation and Prediction System (GDAPS) based on Unified Model (UM).
ACI의 예측 성능은 국내 레이더 관측 자료를 통해 검증되었다. 현재 한국 기상청에서는 인천 공항의 공항 레이더를 제외하고, 총 10 곳의 관측소에서 현업용 기상레이더를 운영 중이다. 레이더 자료는 기본적으로 하나의 관측 지점을 중심으로 방위각과 고도각에 대한 좌표계로 이루어져 있으므로 격자 자료인 ACI의 예측장과 직접적으로 비교하는데 한계가 있다. 이를 해결하기 위해, 오픈소스 형태로 개방된 Python ARM Radar Toolkit의 map to grid 알고리즘(Barnes, 1964)을 사용하여 10개의 관측소의 레이더 자료를 하나의 격자 형태의 데이터로 합성하였다. 먼저, 위도 36oN와 경도 127.5oE를 중심 지점으로 정의하였고, 1 km와 100 m의 수평과 수직 격자로 이루어진 3차원 격자를 설정하였다. 그리고 각 격자점에서 500m 반경 이내의 반사도 관측 값을 거리에 따라 가중치를 두어 내삽하였다.
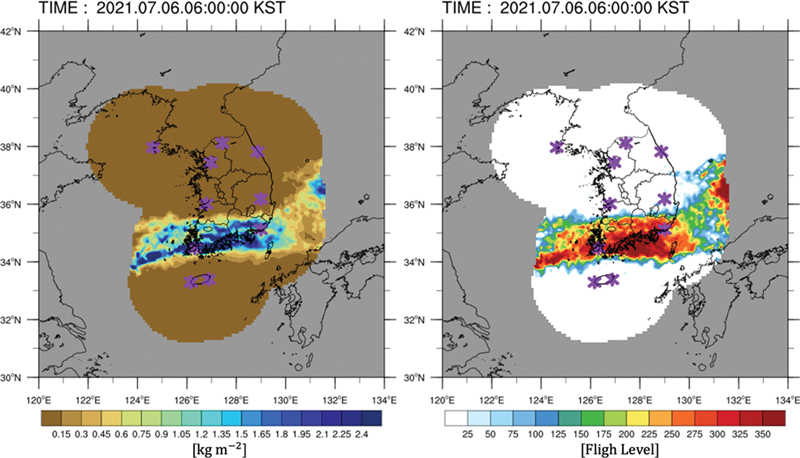
레이더의 반사도는 다양한 기상학적 변수로 변환되어 활용될 수 있다. 경험적인 반사도-강수(R-Z) 방정식을 기반으로 강수량으로 변환될 수 있을 뿐만 아니라 우적의 지름 및 수상체의 개수에 대한 간단한 가정을 통해 연직 적분 액체 수액량(Vertically Integrated Liquid water content, 이하 VIL)으로 계산될 수 있다. VIL은 구름 내의 액체 수상체의 양을 의미하기 때문에 주로 강수를 발생시키는 습윤 대류에서 높게 나타난다. 이 변수는 레이더 자료를 기반으로 폭풍 및 뇌우를 탐지하고 추적하는 기술인 Thunderstorm Identification Tracking Analysis and Nowcasting (TITAN)에서 대류운을 식별하는 데 활용된 바 있다(Dixon and Wiener, 1993). 또한, 반사도는 에코 정상고도(Echo Top Height, 이하 ETH)로 변환되어 대류의 강도 및 위치 분포를 파악하는 데 많이 활용된다. Zhang et al. (2006)은 대류로 인한 강수 지역을 15 dBZ ETH와 30 dBZ ETH을 기준으로 약한 강수 지역과 강한 강수 지역을 나누어 정의하였다. 또한, Delobbe and Holleman (2006)에서는 우박 폭풍을 탐지하기 위해 45 dBZ ETH을 사용하였다. 이처럼 분석 목적 및 분석하고자 하는 대류의 물리적인 특징에 따라서 반사도 기준이 달라질 수 있다. 여기서, 일반적인 대류의 유무를 파악하는데 15dBZ 반사도가 임계 값으로 활용될 수 있다(Awaka, 1998; Zhang et al., 2006; Sohn et al., 2013; Song and Sohn, 2015). Figure 1은 반사도로 산출한 VIL과 15 dBZ ETH의 예시이다. 두 변수는 기본적으로 매우 유사한 공간 분포 및 강도를 보여주고 있다. 그러므로, 두 변수 모두 ACI의 예측 성능을 검증하는데 충분히 활용될 수 있다. 하지만 VIL의 단위(kg m-2)보다 ETH의 단위(비행고도, Flight Level, 이하 FL)가 대류의 강도를 더 직접적으로 표현할 뿐만 아니라 ACI를 해당 단위로 변환하였을 때 예보에 더욱 쉽게 활용될 수 있다는 장점이 있으므로, 본 연구에서는 15 dBZ ETH를 검증 변수로 사용하였다.
2.2 ACI 산출 방법론
전지구 모델에서 실제 대류 현상은 단순히 하나의 변수로 설명하기에는 한계가 있다. 이를 극복하기 위해서는 특정 현상의 물리적 특징과 관련이 깊으며 이를 잘 대변하는 변수들을 동시에 사용하는 것이 바람직하다. 본 연구에서는 기상학적 이론을 바탕으로 대류의 물리적인 특징을 잘 설명하는 대류 가용 잠재에너지(Convective Available Potential Energy, 이하 CAPE), 누적 강수량(Accumulated Precipitation, 이하 APCP), 그리고 상향 장파 복사량(Outgoing Longwave Radiation, 이하 OLR)을 사용하였다. 먼저, CAPE는 공기 덩어리가 단열 과정에서 자유상승고도(Level of Free Convection, 이하 LFC)부터 열적 중립 고도(Equilibrium Level, EL)까지 순식간에 상승하였을 때 발생하는 양의 부력 에너지의 합을 의미한다. 높은 대류가 발달하기 위해서는 충분한 잠재 에너지가 해소되어야 하므로 강한 대류의 대표적인 필요 인자라고 할 수 있다. 또한, 강한 대류 운동이 존재하는 경우에는 습윤한 공기는 빠르게 상승하며 응결한다. 이 과정에서 많은 양의 물방울을 형성되고 강한 호우를 발생시킬 수 있다. 그러므로 많은 양의 누적 강수량은 곧 깊은 대류의 존재를 직접적으로 대변할 수 있다. 마지막 입력 변수인 OLR은 지면에서 대기 중으로 상향 전파되는 복사량을 의미한다. 대류는 상향 방출되는 복사를 막는 역할을 하기 때문에 구름이 많고 높게 발달할수록 OLR은 작게 나타난다. 정리하면, 높은 CAPE와 A PCP, 그리고 낮은 OLR은 깊은 대류를 의미할 수 있다. 앞서 언급한 EPOCH에서도 해당 변수들을 동일하게 사용하여 깊은 대류에 대한 발생 확률을 계산하였다.
ACI를 산출하기 위해서는 서로 다른 입력 변수들을 하나의 지수로 결합하는 과정이 필요하다. 본 연구에서는 3개의 변수를 하나의 연속적인 값으로 변환하기 위해 퍼지-로직(Fuzzy-logic) 방식을 사용하였다. 해당 방법론은 딥-러닝 분야에서도 활발하게 사용되는 논리 알고리즘으로, 특정 사건을 단순히 이진법이 아닌 연속성을 갖는 값으로 표현될 수 있도록 하는데 유용한 방법론이다. Kessinger et al. (2008)은 퍼지-로직 알고리즘을 기반으로 미국 국립해양대기청의 Geostationary Operational Environmental Satellite (GOES) 위성 자료로 관측된 기상 변수들을 하나로 결합하여 해양성 대류 진단 지수인 Convective Diagnosis Oceanic(CDO)를 개발하였다. 이 진단 지수는 내륙뿐만 아니라 해양에서 발생하는 대류의 공간 분포를 파악하기 용이하기 때문에 EPOCH의 예측 성능을 검증하는 데 활용되었다. 뿐만 아니라 레이더 관측 자료를 활용하여 퍼지-로직 방식 기반 대류 세포 추적 시스템인 Fuzzy-logic Algorithm for Storm Tracking (FAST)가 개발된 바 있다(Jung and Lee, 2015). 해당 연구에서는 레이더 관측자료에서 산출한 대류 세포의 이동속도, 반사도 변화율, 대류 면적 변화율, 그리고 축 변형율을 결합하였다.
본 연구에서 개발된 ACI도 같은 방식을 통해 계산된다. Figure 2는 그 과정을 설명하는 모식도이다. 서로 다른 변수들이 결합되기 위해서는 동일한 범위를 갖는 값으로 변환되어야 한다. 이 과정에서 각 변수의 멤버십 함수(Membership Function, 이하 MF)가 정의되며, 이 MF는 각 변수들을 0~1의 새로운 값으로 할당한다. 이러한 값들은 멤버십 값(Membership value, 이하 M)으로 정의되며, 각 변수가 갖는 깊은 대류에 대한 잠재도를 의미한다. 입력 변수인 CAPE, APCP, OLR의 MF와 M은 각각 MFCAPE, MFAPCP, MFOLR, 그리고 MCAPE, MAPCP, MOLR으로 표현된다. 앞서 설명한 기상학적 이론에 따라 CAPE와 APCP는 높을수록 1에 가까운 MCAPE와 MAPCP 값으로 할당되는 반면, OLR은 낮을수록 MOLR이 1에 가까워진다. 이렇게 산출된 각 변수의 잠재도 값들은 합이 1이 되는 특정 상수조합[α (CAPE), β (APCP), γ (OLR)]에 따라 가중 평균 되어 하나의 값으로 계산된다. 그러므로 최종적인 잠재도를 의미하는 ACI는 1에 가까울수록 깊은 대류의 발생을 의미한다.
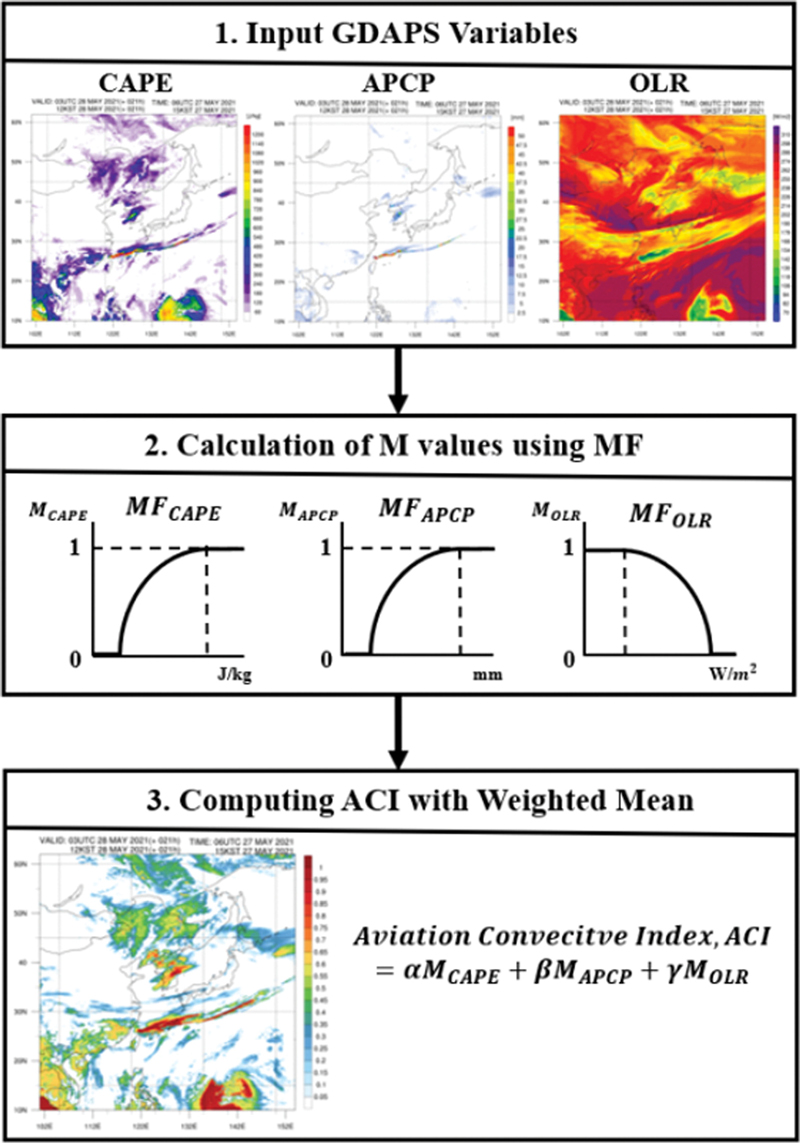
A flow chart on computing ACI based on fuzzy-logic algorithm. Here, CAPE, APCP, and OLR indicates the convective available potential energy, the accumulated precipitation, and the outgoing longwave radiation. M and MF means the membership value and the membership function. And, α, β, and γ are the weight coefficients for CAPE, APCP, and OLR.
이러한 계산 과정에서 가중치 조합은 최종적인 ACI 계산 결과에 큰 영향을 끼친다. 동일한 입력 변수 값을 사용하더라도 사용되는 가중 상수에 따라 최종적인 ACI 값은 충분히 다르게 계산될 수 있다. 이는 특정 변수의 가중치가 높을 수록 해당 변수의 시공간 분포가 ACI 결과에 더 많이 반영되기 때문이다. 그러므로 가중 상수의 조합은 각 변수의 대류 예측 성능을 고려하여 결정하는 것이 바람직하다.
퍼지-로직 알고리즘에 사용되는 MF는 각 변수의 확률 분포를 근거로 구축되었다. 먼저, 한반도 주변 지역(위도 30~42oN, 경도 121~134oE)을 중심으로 2021 동안의 6~48시간 예측장에서 나타난 입력 변수들의 백분위 수를 살펴보았다(Table 2). 본 연구에서는 각 변수의 백분위 수를 기반으로 위험 범위를 설정하였고, 해당 구간 내에서 MF를 구축하였다. 여기서 위험 범위는 평균 및 다양한 백분위 수 값을 기준으로 다르게 설정될 수 있다. 그리고 이 범위에 따라 멤버십 함수와 특정 변수 값이 갖는 잠재도가 다르게 결정되기 때문에 예측 성능에도 큰 영향을 끼친다. 예를 들어, 위험 범위를 높게 설정하는 경우에는 해당 구간 내에서 낮은 값들은 깊은 대류를 예측한 격자수가 급격히 감소하기 때문에 예측 성능이 크게 감소한다. 그러므로, 본 연구에서는 다양한 위험 범위를 비교한 후, 그 중 예측 성능이 상대적으로 높게 나타났던 범위를 임의로 위험 범위로 정의하였다. 결론적으로, CAPE와 APCP는 평균으로부터 단일 표준 편차에 해당하는 상위 84.1% 값부터 상위 99% 값까지, 그리고 OLR은 1% 값부터 15.9% 값을 위험 범위로 정의하였고, 이렇게 1년 기간에 대해 정의된 CAPE, APCP, OLR의 위험 범위는 각각 51.8~684.19 J kg-1, 0.281~10.152 mm, 그리고 194.062~137.156W m-2이다.

Percentile of CAPE, APCP, and OLR in 1-yr period of 2021. Bracket correspond to the percentile of OLR. Bold letters represent the severe range.
MF는 0부터 1까지 값으로 이루어진 선형 함수로 정의되며, CAPE와 APCP는 위험 범위에서 높을수록, 반면에 OLR은 낮을수록 1에 가까운 값으로 할당되는 것이 이상적이다. 본 연구에서는 MF들을 누적 분포함수(Cumulative Distribution Function, 이하 CDF)를 기반으로 구축하였다. 자세히 말하면, 각 변수의 위험 범위를 100개의 구간(bin)으로 나누어 각 구간에 대응되는 발생 빈도를 분석하였다. 여기서 발생 빈도는 본 연구에서 다루는 2021년 1년 기간 동안 앞서 정의된 한반도 주변 도메인 내에서 산출되었다. 그리고 각 변수의 발생 빈도에 대한 CDF를 구축하여, 이를 따르는 선형식을 구하고자 하였다. 본 연구에서는 각 변수의 CDF를 따르는 다항식 형태의 회귀식을 최소 제곱법(Least Square Error)을 통해 구하였다. 즉, 근사적으로 구하려는 방정식과 CDF 값의 오차들의 제곱의 합이 최소가 되도록 하는 회귀 방정식을 MF로 정의하였다. Figure 3은 앞서 설명한 방식을 토대로 구축한 각 변수의 발생 빈도에 대한 CDF이다. 각각의 멤버십 함수에서 최소 및 최대 구간 값은 각 변수의 위험 범위를 의미하여 CDF 위에 위치한 파란선은 최소 제곱법을 통해 계산된 다항식 형태의 MF이다. 여기서 다항식은 차수가 높을수록 더욱 정교한 피팅이 가능하지만, 본 연구에서는 가장 단순한 1차부터 복잡한 8차까지의 다항식 형태의 회귀식들을 비교한 후, CDF에 적절히 적합 되면서 적은 시간이 소요되는 6차 방정식 형태를 선정하였다(Table 3). 이렇게 정의된 MFs들을 통해 서로 다른 3개의 변수 값은 하나의 ACI 값으로 계산되며, 이는 Eqs. (1)-(4)으로 표현된다. 본 연구에서는 지수를 최적화하기 이전에 먼저 균일한 가중 상수(α = 0.333, β = 0.333, γ = 0.333)를 가정하였다. 이는 곧 모든 변수가 동일한 중요도 가졌다는 의미이다. 여기서 균일한 가중치 조합을 적용시켜 구한 ACI를 최적화 이전의 ACI (No Optimized ACI, 이하 ACINoOpt)라고 정의하였다.
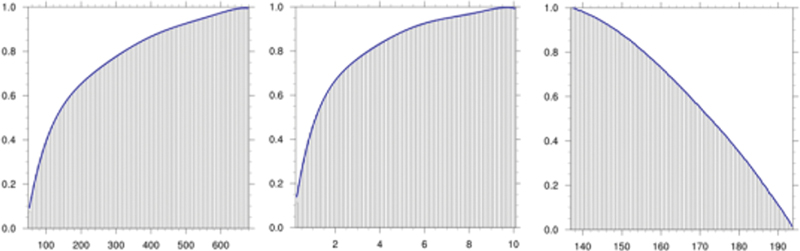
Cumulative Distribution Function of CAPE (left), APCP (middle), and OLR (right). The Membership Function is indicated by the blue line in each plot.
| (1) |
| (2) |
| (3) |
| (4) |
각 변수의 가중치는 최종적인 ACI 값에 대한 기여도를 의미하기 때문에 가중 상수 조합은 ACI의 예측 성능에 크게 기여할 수 있다. 그러므로 예측 성능이 가장 높은 최적의 상수 조합을 찾는 과정이 필요하다. 각각의 상수를 0.05 단위로 나누었을 때 α + β + γ = 1 조건을 만족하는 모든 경우의 수는 총 231가지이다. 본 연구에서는 통계적 분석법을 기반으로 모든 경우의 수를 비교하였다.
본 연구에서는 최적화와 예측 성능 검증 과정에서 다양한 통계치들이 사용되었다. 먼저, Probabilistic Of Detection (PODY)는 특정 현상의 전체 발생 횟수 대비 발생을 예측한 경우의 비율을 의미하며, 적중률이라고 한다[Table 4와 Eq. (5)]. PODY는 발생한 현상에 대해 얼마나 발생 예측을 성공하였는지 판단하는데 사용된다. 다음으로 Probability Of False Detection(POFD)는 발생하지 않은 현상을 발생한다고 예측한 비율을 의미한다. 예측하였지만 발생하지 않은 횟수를 전체 발생하지 않은 횟수로 나누어 계산할 수 있다[Table 4와 Eq. (6)]. 마지막으로 검증 단계에서 사용되는 True Skill Statistics (TSS)는 PODY와 POFD의 차이로 나타낼 수 있으며, 특정 현상에 대해 발생을 예측한 비율과 발생하지 않은 것에 대해 예측을 실패한 비율의 차이를 의미한다[Eq. (7)]. 그러므로 해당 값이 클수록 이상적인 예측을 의미한다.
| (5) |
| (6) |
| (7) |
최적화 및 검증은 2021년, 1년 기간에 대해 이루어졌으며, 분석에는 수신자 조작 특성 곡선(Receiver Operating Characteristics curve, 이하 ROC curve)이 사용되었다. 특정 가중치 조합으로 계산된 ACI의 6시간 예측 결과와 레이더의 15 dBZ ETH와 비교하였다. 1간 총 1460개의 시간대가 고려되었으며, 이 중 모든 레이더 관측소에서 동시에 결측이 발생했던 날짜를 제외하여 총 1459개 시간대의 관측장과 예측장이 활용되었다. 본 연구에서는 관측장과 예측장을 정량적으로 비교하기 위해 두 자료를 0.1o × 0.1o의 해상도로 재격자화하는 과정을 거쳤다. 또한, UM-GDAPS의 변수들은 3시간 단위로 제공되므로 정확한 비교를 위해 최근 3시간 평균 15 dBZ ETH로 검증을 진행하였다. 또한, ROC curve 분석은 비교하는 두 자료가 True/False로 이루어진 이분법적인 자료일 때 가능하다. 먼저, 관측장에서는 깊은 대류의 발생 유무를 15 dBZ ETH의 FL250 고도를 기준으로 정의하였다. 해당 고도는 미국 항공기기상센터(Aviation Weather Center)에서 A ir Traffic Management (ATM)의 의사 결정을 돕기 위해 현업으로 운영 중인 Traffic Flow Management (TFM) Convective Forecast (TCF) 시스템에서 표출하는 최소 비행고도 기준이다(AWC).
본 연구에서 최종적으로 예측하고자 하는 이벤트는 15 dBZ ETH이 FL250 이상인 깊은 대류 영역이다. 하지만 해당 기준을 만족하는 이벤트는 드물게 발생하기 때문에 PODY와 POFD를 계산하는 데 사용되는 격자 수를 유사하게 맞춰주고자 하였다. 이를 위해, 본 연구에서는 두 통계치를 15 dBZ가 FL0보다 높은 지역에 한해서 계산하였다. ACI 값을 0.0부터 1.0까지 0.01 단위로 나누어 각 지수 값에 대한 PODY와 POFD를 산출하였다. 그리고 1.0과 0.0 값에 대응되는 우측 상단과 좌측 하단의 점을 이어 POFD에 대한 PODY의 함수로 ROC curve를 표현하였다. 해당 방식은 검증 과정에서도 동일하게 적용하였다.
ROC curve가 이루는 면적은 Area Under the Curve(이하 AUC) 로 정의되는데, 그 값이 1에 가까울 때 시스템의 예측성이 100%이며 특정 현상을 완벽히 분리해 예측해 낼 수 있다는 것을 의미한다. 본 연구에서는 모든 가중치 조합으로 산출된 AUC 값들을 비교하였다(Table 5). 상위 10개의 조합들을 살펴보면, CAPE와 OLR의 가중 상수는 매우 높은 반면 A PCP의 가중치는 매우 낮거나 0인 것을 알 수 있다. 이는 1년 전체 기간에 대해 고정된 가중치 조합을 사용할 때, 수치모델에서 제공되는 C A PE와 OLR의 예측 장을 주로 사용하는 것이 깊은 대류를 예측하는 데 유리하다는 의미이다. 하지만 이러한 결과는 1년 기간동안 항상 A PCP가 깊은 대류를 거의 예측하지 못한다는 것을 의미하지 않는다. 여기서 고려한 AUC는 특정 잠재도 값에서의 PODY와 POFD의 값과 상관없이 ROC 곡선이 이루는 면적을 의미하며, 이는 다양한 경우에서 증가할 수 있다. 예를 들면, PODY가 증가하고 POFD가 감소하는 이상적인 경우 이외에도, PODY와 POFD가 모두 증가하지만 PODY가 더 큰 폭으로 증가하는 경우와 PODY와 POFD가 모두 감소하지만 POFD가 더 감소하는 경우도 존재한다. 본 연구에서는 오직 장기간에 대한 최종적인 AUC 값만 단순히 비교하였기 때문에 위 경우들을 구분하지 않았다. 그러므로, 계절과 같은 특정 기간을 따로 고려한다면 충분히 다른 결과가 나올 수 있다. 이와 관련된 내용은 파트 2에서 주로 다룰 것이다. Table 5에서 α = 0.45, β = 0.05, γ = 0.50 일 때 AUC가 0.7662로 최댓값이 나타났으며, 이 1년 기간에 대한 최적의 가중치 조합을 적용한 ACI를 Year Optimized ACI(이하 ACIYrOpt)라고 정의하였다.
3. 예측 성능 검증
3.1 ACINoOpt 예측 성능
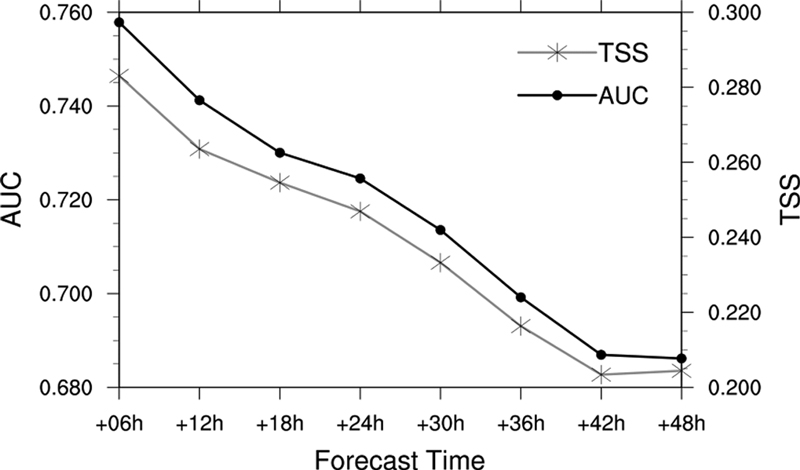
먼저, 균일한 가중치로 설정된 ACINoOpt의 예측 성능에 대한 통계적 검증을 수행하였다. Figure 4는 예측 기간 별 ACINoOpt의 ROC curve와 이에 해당되는 AUC 값을 보여준다. 여기서 표시된 점은 우측 상단으로부터 순서대로 ACINoOpt가 0.25, 0.50, 그리고 0.75에 대응되는 점이다. 다양한 예측 기간의 곡선들을 비교해보면, 예측 기간이 가장 짧은 6시간 예측 결과가 가장 넓은 곡선을 보여주며, AUC 값이 0.758로 가장 높았다. 또한, 예측 기간이 길어지면서 곡선의 면적이 일관적으로 감소하여 AUC가 꾸준히 감소하는 것을 볼 수 있다. 즉, ACI의 예측 성능은 예측 기간이 길어질수록 감소하는 경향을 보인다. 결론적으로, 48시간 예측 결과의 AUC 값은 0.686이었다.
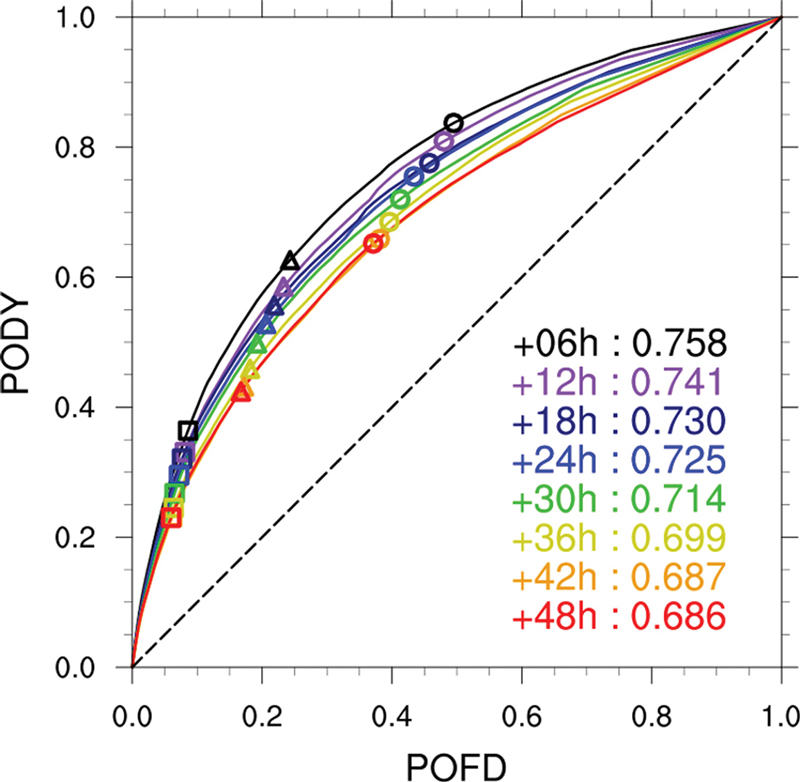
ROC curves of ACINoOpt for 1-yr with each forecast time. The numbers are the AUC values. And, the circle, triangle, and square marker indicate the ACI of 0.25, 0.50, and 0.75, respectively.
해당 그림에서 곡선 위의 점들을 통해, 예측 기간에 따라 곡선이 어떻게 이동하는지 파악해 볼 수 있다. 곡선 위의 점들은 좌측 하단으로 이동하면서 곡선이 이루는 면적이 감소하였다. 즉, 이는 예측 기간이 길어지면서 전반적으로 ACI의 PODY와 POFD 모두 감소한다는 의미이다. 특히, POFD의 감소 폭보다 PODY의 감소폭이 더욱 컸다. 이는 예측 기간이 길어지면서 깊은 대류가 발생하지 않은 지역에 대해선 예측성이 약간 증가하였지만, 반대로 깊은 대류가 발생한 지역 내에선 발생에 대한 예측성이 크게 감소하였다는 의미이다. 이것이 AUC 값이 감소한 이유이다.
예측성을 평가하는 과정에서 AUC 뿐만 아니라 전체 임계값에 대한 평균 TSS를 추가로 비교하였다. 두 통계치를 보면, AUC 뿐만 아니라 평균 TSS 또한 예측 기간에 따라 전반적으로 감소하는 경향이 나타났다(Fig. 5) 평균 TSS는 6시간 예측일 때 0.283을 시작으로 48시간 예측 결과에서는 0.204로 꾸준히 감소하였다. 이처럼 두 통계치 모두 감소하는 이유는 ACI는 오직 수치 예보모델 예측 결과를 사용하여 산출되기 때문이다. 그러므로 ACI의 예측 성능은 입력 자료로 사용되는 수치모델의 예측성에 크게 의존할 수 밖에 없으며, 예측 기간에 따라 성능이 감소하는 수치모델의 특징이 ACI에서도 나타난 것을 알 수 있다.
3.2 ACIYrOpt 예측 성능
다음은 ACINoOpt와 동일한 MF를 사용하지만 2021, 1년 기간에 대한 최적의 가중치를 적용한 ACIYrOpt의 예측 성능을 검증한 결과이다. 먼저, 두 ACI의 6시간, 24시간, 그리고 42시간 예측 결과에 대한 ROC curve들을 비교하였다(Fig. 6) 앞서 설명한 것처럼 가중치의 최적화는 6시간 예측 결과만을 사용하여 수행되었다. 하지만, 단기간에 대한 예측뿐만 아니라 24시간 이상의 더 장기간의 예측 기간에서도 최적화로 인한 예측 성능 향상이 나타났다. 해당 그림에서도 최적화된 ACIYrOpt의 곡선이 모든 예측 기간에서 기존보다 좌측 상향으로 이동하며 넓어진 것을 확인할 수 있다. 이에 따라 AUC 값이 모든 예측 기간에서 증가하였다.
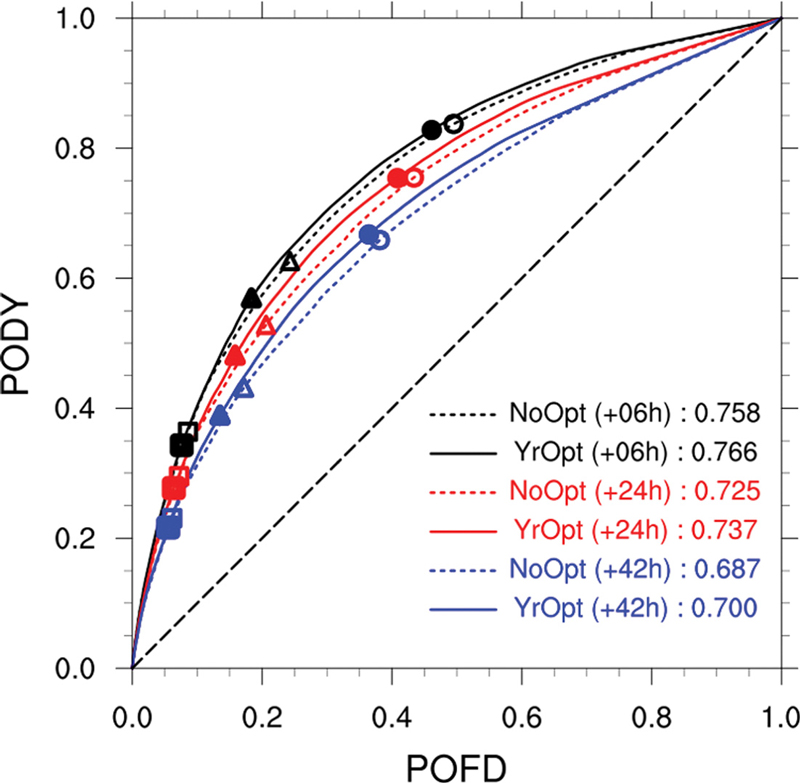
ROC curves of ACIYrOpt (solid line) and ACINoOpt(dashed line) of 6-hour (black), 24-hour (red), and 42-hour (blue) forecast. The circle, triangle, and square marker indicate the ACI of 0.25, 0.50, and 0.75, respectively.
최적화 이후 특정 예측 기간뿐만 아니라 6시간부터 48시간까지의 모든 기간에서 AUC와 평균 TSS 모두 증가하였다(Fig. 7). 해당 그림에서 파선으로 표현된 최적화 이전의 AUC와 TSS는 Fig. 5의 선들과 동일하다. 여기서 흥미로운 점은 6시간 예측장을 통해 최적화를 거쳤음에도 그 외의 장기간 예측 기간에도 마찬가지로 예측 성능이 동일하기 증가했다는 점이다. 특히, AUC 값은 단기간인 6시간 예측보다 더 장기간 예측에서 더 높은 증가를 보였다. 전체 예측 기간에 대한 평균 TSS는 기존의 ACINoOpt이 0.238, 그리고 ACIYrOpt은 0.248로 기존 대비 4.20 % 향상된 결과를 보였다. 뿐만 아니라, ACINoOpt의 평균 AUC는 0.717인 반면 최적화 이후 ACIYrOpt은 0.729로 증가하면서 기존 대비 1.67% 향상되었다.
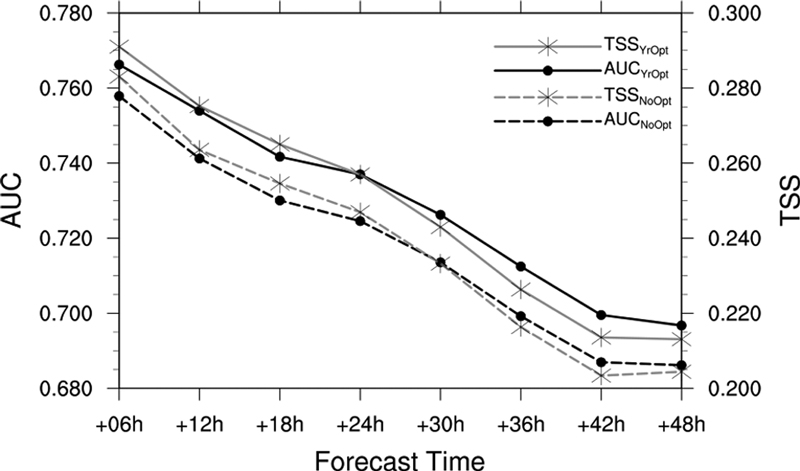
AUC (black) and TSS (grey) values of ACINoOpt (dashed line) and ACIYrOpt (solid line) for each forecast time. The dashed lines are same as the solid lines in Fig. 5.
최적화를 통해, 어떻게 예측 성능이 향상되었는지는 최적화 전후 PODY와 POFD의 변화를 통해 이해할 수 있다. Figure 8은 이를 설명하는 모식도이다. 최적화 전후 통계치들을 비교해 보았을 때, PODY가 증가하고 POFD는 감소하는 경우에는 모든 점들이 2사분면에 위치하게 된다. 이 경우에는 ROC 곡선을 이루는 점들이 모두 좌측 상단으로 이동하기 때문에 곡선이 이루는 면적이 증가함을 알 수 있다. 이처럼 이상적인 상황이 아니더라도 AUC 값은 충분히 증가할 수 있다. 해당 그림에서 1사분면과 3사분면의 상단 영역은 각각 PODY가 POFD 보다 더 큰 폭으로 증가하거나 POFD가 PODY보다 더 큰 폭으로 감소하는 경우를 의미한다. 이 경우에도 ROC 곡선이 이루는 면적을 증가할 수 있다. 반면에, PODY가 감소하지만 POFD는 증가하는 경우, 곡선을 이루는 점들은 모두 4사분면 쪽으로 우측 하향하기 때문에 예측 성능은 크게 감소한다. 뿐만 아니라 1사분면과 3사분면의 하단 영역과 같이 PODY가 증가하지만 POFD가 더 많이 증가하거나, 또는 POFD가 감소하지만 PODY가 더 크게 감소할 때도 AUC 값은 감소한다. 해당 그림에서 점선으로 표시된 대각선의 위쪽(Fig. 8에서 +지역)에 위치한 점들의 개수가 더 많을수록, AUC이 더 많이 증가할 수 있다. 또한, 최적화 이후 POFD가 더 증가하여 대부분의 점들이 1사분면에 위치한 경우에는 오탐률이 증가하여 실제로 발생하지 않은 영역에 대해 상대적으로 더 과대 예측한다고 해석할 수 있다. 반대로, 적중률이 감소하여 대부분의 점이 3사분면에 존재한 경우에는, 최적화된 ACI가 발생한 영역에 대해 기존보다 더 과소 예측한다는 의미이다.

Diagram (left) for interpreting the plot of change of PODY and POFD and Scatter plot (right) of change of PODY and POFD between ACIYrOpt and ACINoOpt (ACIYrOpt-ACINoOpt) for 06-hour (black), 24-hour (red), 42-hour (blue) forecast time. And circle, triangle, and square marker indicates the ACI of 0.25, 0.50, and 0.75 for 06-hour forecast and these are associated with the change of PODY and POFD between ACIYrOpt and ACINoOpt of the black markers in Fig. 6.
1년 기간의 최적화 과정을 통한 ACI의 PODY와 POFD의 변화를 보면, 대부분의 점들이 3사분면에 위치한 것을 알 수 있다(Fig. 8). 이는 적중률과 오탐률 모두 감소한 것을 의미한다. 그럼에도 불구하고 AUC가 증가할 수 있었던 이유는 PODY보다 POFD가 더 크게 감소하였기 때문이다. 실제로 대각선을 기준으로 위쪽과 아래쪽 지역의 점의 개수를 비교해 보면, 예측 성능을 향상시킬 수 있는 (+) 영역의 점들이 모든 예측 기간에서 더 많은 것을 알 수 있다. 여기서, 대표적인 세 예측 기간들을 비교해보면, 6시간과 24시간 예측 결과에서는 (+) 영역의 점과 (-) 영역의 점의 개수의 차이는 20개로 동일하다. 하지만 42시간 예측 결과에서는 그 차이가 10개로 작다. 그럼에도 불구하고 6시간 예측보다 42시간 예측 때의 AUC 증가량이 상대적으로 더 컸다(Figs. 6, 7). 그 이유는 최적화 과정에서 PODY는 증가하고 POFD는 감소하는 이상적인 점들이 더 많이 존재했기 때문이다. 실제로 0.25를 포함한 낮은 ACI 구간의 점들은 대부분 2사분면에 위치해 있었으며, Fig. 6에서 낮은 ACI 점들의 위치 변화를 보면 대부분 좌측 상향되어 AUC 값을 증가시키는 형태를 보인다.
4. 결 론
뇌우 및 깊은 대류는 난류, 뇌우, 다운버스트 같은 다양한 위험 기상을 발생시키기 때문에, 안전한 항공기 운항을 위해서는 대류의 정확한 시공간 분포의 예측이 필수적이다. 이를 위해, 미국에서는 EPOCH, 그리고 WAFS Cb와 같은 뇌우 예측 시스템들이 개발되었다. 본 연구에서는 국내의 공항 지역뿐만 아니라 동아시아를 포함한 공역 지역에 대한 깊은 대류 영역 예측을 위해, 국내 현업 예보모델 중 하나인 UM 모델 기반 전지구예보모델, GDAPS를 사용하여 새로운 대류 예측 지수, ACI를 개발하였다.
본 연구를 통해 처음으로 제안된 이 지수는 강한 대류의 물리적 특성을 잘 대변하는 CAPE, APCP, 그리고 OLR로부터 산출된다. 각각의 변수는 대류 특성과 관련이 깊기 때문에, 독립적인 예측 인자로 활용될 수 있다. 하지만, 전-지구 모델은 실제 대류의 발달 과정을 설명하는 데 한계가 있다. 이를 극복하기 위해, 딥-러닝 분야에서 활발히 사용되고 있는 퍼지-로직 결합 알고리즘을 사용하여 하나의 최적화된 ACI로 변환하였다. 결합 과정에서 사용되는 MF와 가중상수는 한반도 지역을 중심으로 1년 기간에 대해 통계적 방법을 사용하여 최적화하였다. 결론적으로 최대 AUC 값을 지닌 가중 상수 조합은 0.45 (CAPE), 0.50 (APCP), 그리고 0.05 (OLR)였다. 이렇게 개발된 ACI는 국내 레이더 관측 자료를 통해 검증되었다. 이 과정에서 15 dBZ ETH가 사용되었으며, 1년 기간에 대해 검증이 수행되었다.
ROC curve 분석에서 최적화 이전의 ACINoOpt보다 장기간에 대해 최적화된 ACIYrOpt가 더 높은 예측 성능을 보였다. 전체 예측 기간에 대한 평균 AUC는 기존 ACINoOpt이 0.717에서 ACIYrOpt는 0.729로 기존 대비 1.67% 향상되었으며, 평균 TSS는 최적화 과정을 통해 4.20%의 향상을 보였다. 특히, 최적화에 사용된 6시간 예측 결과보다 42시간 예측 결과에서 상대적으로 더 높은 성능 향상이 나타났다. ACIYrOpt는 기존의 ACINoOpt보다 PODY와 POFD 모두 전반적으로 감소하였지만, POFD이 더 큰 폭으로 감소되면서 AUC가 증가하였다. 하지만, 가장 높은 AUC 증가폭을 보였던 42시간 예측에서는 낮은 값 구간에서 POFD는 감소하고 PODY가 증가하는 이상적인 최적화 결과를 보였다.
대류 현상뿐만 아니라 이를 대변하는 변수들은 계절에 따라 발생 강도 및 빈도가 다르다. 그러므로, 깊은 대류를 더 정확히 예측하기 위해서는 이러한 계절 변동성을 고려해야 한다. 특히, 본 연구에서 개발된 ACI는 산출 과정에서 각 변수의 누적분포함수를 기반으로 정의된 MF들이 사용되기 때문에 계절에 맞는 MF와 가중 상수를 사용할 필요가 있다. 1년 장기간 최적화가 갖는 한계와 계절별 최적화의 필요성, 계절별 최적화된 ACI의 통계적 검증, 그리고 사례 분석을 통한 정성적 검증은 본 연구의 파트 2에서 다루고 있다.
Acknowledgments
본 논문의 질적 향상을 위해 좋은 의견들을 제시해주신 두 심사위원 분들께 감사의 말씀을 전합니다. 이 연구는 기상·지진 See-At 기술개발연구사업(KMI2020-01910)의 지원과 기상청 「차세대 항공교통 지원 항공기상 기술개발(NARAE-Weather)」(KMI2022-00310과 KMI2022-00410)의 지원으로 수행되었습니다.
References
- Awaka, J., 1998: Early results on rain type classification by the Tropical Rainfall Measuring Mission (TRMM) precipitation radar. Proc. 8th URSI Commission F Triennial Open Symposium, 143-146.
- AWC : Product Description Document Traffic Flow Management (TFM) Convective Forecast (TCF). [Available online at https://nws.weather.gov/products/PDD/TCFPDD.pdf, ].
-
Barnes, S. L., 1964: A technique for maximizing details in numerical weather map analysis. J. Appl. Meteor. Climatol., 3, 396-409.
[https://doi.org/10.1175/1520-0450(1964)003<0396:ATFMDI>2.0.CO;2]

-
Clark, A. J., J. S. Kain, P. T. Marsh, J. Correia Jr, M. Xue, and F. Kong, 2012: Forecasting tornado pathlengths using a three-dimensional object identification algorithm applied to convection-allowing forecasts. Wea. Forecasting, 27, 1090-1113.
[https://doi.org/10.1175/WAF-D-11-00147.1]

-
Delobbe, L., and I. Holleman, 2006: Uncertainties in radar echo top heights used for hail detection. Meteor. Appl., 13, 361-374.
[https://doi.org/10.1017/S1350482706002374]

-
Dixon, M., and G. Wiener, 1993: TITAN: Thunderstorm identification, tracking, analysis, and nowcasting—A radar-based methodology. J. Atmos. oceanic technol., 10, 785-797.
[https://doi.org/10.1175/1520-0426(1993)010<0785:TTITAA>2.0.CO;2]

-
Gagne, D. J., A. McGovern, S. E. Haupt, R. A. Sobash, J. K. Williams, and M. Xue, 2017: Storm-based probabilistic hail forecasting with machine learning applied to convection-allowing ensembles. Wea. Forecasting, 32, 1819-1840.
[https://doi.org/10.1175/WAF-D-17-0010.1]

- ICAO, 2012: Seventh Meeting of the World Area Forecast System Operations Group (WAFSOPSG) Lima, Peru, 59 pp [Available online at https://www.icao.int/safety/meteorology/WAFSOPSG/WAFSOPSG%20Meetings%20Metadata/WAFSOPSG.7.Final.Report.pdf, ].
- Jahn, D. E., I. L. Jirak, A. Wade, and J. Milne, 2022: Storm Mode and Tornado Potential Determination Using Statistical Moments of Updraft Helicity Distribution. 27th Conf. Numerical Wea. Pred., Houston, TX, Amer. Meteor. Soc, 5 pp.
-
Jung, S.-H., and G. Lee, 2015: Radar-based cell tracking with fuzzy logic approach. Meteor. Appl., 22, 716-730.
[https://doi.org/10.1002/met.1509]

-
Kessinger, C., M. Donovan, R. Bankert, E. Williams, J. Hawkins, H. Cai, N. Rehak, D. Megenhardt, and M. Steiner, 2008: Convection diagnosis and nowcasting for oceanic aviation applications. Remote Sens. Appl. Aviation Wea. Hazard Detection and Decision Support, 7088, 77-88.
[https://doi.org/10.1117/12.795495]

- Melling, L. D., A. G. Laing, M. S. Wandishin, J. E. Hart, and M. A. Petty, 2019: Ensemble Prediction of Oceanic Convective Hazards (EPOCH) Assessment: Part II. NOAA, 62 pp [Available online at https://repository.library.noaa.gov/view/noaa/22921/noaa_22921_DS1.pdf, ].
-
Sobash, R. A., J. S. Kain, D. R. Bright, A. R. Dean, M. C. Coniglio, and S. J. Weiss, 2011: Probabilistic forecast guidance for severe thunderstorms based on the identification of extreme phenomena in convectionallowing model forecasts. Wea. Forecasting, 26, 714-728.
[https://doi.org/10.1175/WAF-D-10-05046.1]

-
Sobash, R. A., G. S. Romine, C. S. Schwartz, D. J. Gagne, and M. L. Weisman, 2016: Explicit forecasts of low-level rotation from convection-allowing models for next-day tornado prediction. Wea. Forecasting, 31, 1591-1614.
[https://doi.org/10.1175/WAF-D-16-0073.1]

-
Sohn, B. J ., G.-H. Ryu, H.-J. Song, and M. L. Ou, 2013: Characteristic features of warm-type rain producing heavy rainfall over the Korean Peninsula inferred from TRMM measurements. Mon. Wea. Rev., 141, 3873-3888.
[https://doi.org/10.1175/MWR-D-13-00075.1]

-
Song, H. J., and B.-J. Sohn, 2015: Two heavy rainfall types over the Korean peninsula in the humid East Asian summer environment: A satellite observation study. Mon. Wea. Rev., 143, 363-382.
[https://doi.org/10.1175/MWR-D-14-00184.1]

- Wendt, N. A., I. L. Jirak, and C. J. Melick, 2016: Verification of severe weather proxies from the NSSL-WRF for hail forecasting. 28th Conf. on Severe Local Storms, 15 pp [Available online at https://www.spc.noaa.gov/publications/wendt/UH-hail.pdf, ].
-
Zhang, C.-Z., H. Uyeda, H. Yamada, B. Geng, and Y. Ni, 2006: Characteristics of mesoscale convective systems over the east part of continental China during the Meiyu from 2001 to 2003. J. Meteor. Soc. Japan. Ser. II, 84, 763-782.
[https://doi.org/10.2151/jmsj.84.763]