
한반도 지상 풍속의 장기 추세 추정: 관측 자료의 물리적 및 통계적 보정
Abstract
The long-term trend of surface wind speed in Korea is estimated by correcting wind measurements at 29 KMA weather stations from 1985 to 2019 with physical and statistical homogenization. The anemometer height changes at each station are first adjusted by applying physical homogenization using the power-law wind profile. The statistical homogenization is then applied to the adjusted data. A standard normal homogeneity test (SNHT) is particularly utilized. Approximately 40% of inhomogeneities detected by the SNHT match with the sea-level-height change of each station, indicating that an SNHT is an effective technique for reconciling data inhomogeneity. The long-term trends are compared with homogenized data. Statistically significant negative trends are observed along the coast, while insignificant trends are dominant inland. The mean trend, averaged over all stations, is -0.03 ± 0.07 m s-1 decade-1. This insignificant trend is due to a trend change across 2001. A decreasing trend of -0.10 m s-1 decade-1 reverses to an increasing trend of 0.03 m s-1 decade-1 from 2001. This trend change is consistent with mid-latitude wind change in the Northern hemisphere, indicating that the long-term trend of surface wind speed in Korea is partly determined by large-scale atmospheric circulation.
Keywords:
Surface wind speed, linear trend, homogenization1. 서 론
지상 풍속은 기후변화에 의해 “wind stilling”이라고 알려진 전지구적인 감소 추세를 보이고 있다(Roderick et al., 2007). 이러한 감소 추세는 평균적으로 –0.14 m s-1 decade-1로 보이고 있으며(McVicar et al., 2012), 지역별로도 뚜렷하다고 알려져 있다(Wu et al., 2018). 국내에서도 이러한 감소 추세가 확인되고 있다(Seo et al., 2018; Chen et al., 2020). 반면 몇몇 연구에서는 이러한 지상 풍속이 약해지고 있는 추세가 최근 다시 회복하고 있다는 추세의 변화가 보고되고 있어 정확한 추세를 파악하는 것이 필요하다(e.g. Azorin-Molina et al., 2018a; Zeng et al., 2019; Zhang and Wang, 2020).
그러나 장기간 관측 자료에는 관측소 위치 변화, 관측 기기 변경 및 고장, 관측 간격 변화 등 비기후학적인 요인들이 포함되어 있어 분석 과정에 주의가 필요하다(Venema et al., 2018; Azorin-Molina et al., 2018b). 관측 자료에 포함된 이러한 비균질성을 물리적 및 통계적인 방법으로 보정하여 자료의 신뢰도를 확보할 수 있다. 물리적인 보정은 비균질성을 만들어 낸 원인에 대한 기록을 이용하는 방식으로, Wan et al. (2010)에서는 풍속계 고도 변경에 의한 비균질성을 고도에 따른 풍속 분포를 이용하여 보정하였다. 그러나 관측 환경에 대한 기록이 충분하지 않을 경우 비균질성을 물리적으로 보정하는 것은 한계가 있다. 이를 극복하기 위해 다양한 통계적 보정 기법들이 개발되어 왔다. 대표적으로 Von Neumann’s ratio test (Von Neumann, 1941), Pettitt’s test (Pettitt, 1979), Buishand’s test (Buishand, 1982), Standard Normal Homogeneity Test (SNHT; Alexandersson, 1986) 등이 있다. 그 중에서도 SNHT는 시계열 자료의 첫 부분과 끝 부분에 존재하는 비균질성까지 찾을 수 있는 장점이 있다(Martínez et al., 2010).
기상청 종관관측시스템(Automatic Synoptic Observation System, ASOS) 관측 자료에서도 다양한 비기후학적인 요인에 의한 오차가 존재한다. 일례로 풍속계 고도는 각 관측소 별로 3회 정도 변경되었다(Choi et al., 2021). 이는 장기 추세를 결정하는 데 큰 영향을 미친다. 하지만 관측자료의 비균질성을 보정하고 장기 추세를 분석한 연구는 많지 않다. Kim and Paik (2015)과 Kim et al. (2020)에서 풍속계 고도에 대한 공간적인 비균질성은 보정하였으나, 분석 기간동안 발생한 풍속계 고도 변경에 따른 시간적인 비균질성은 보정하지 않았다. 최근 Choi et al. (2021)에서 동일한 문제점을 확인하고, 풍속계 고도 변경에 대한 시공간적인 비균질성을 모두 보정하여 기존 연구를 보완하였다. 그러나 여기서 사용한 물리적 보정은 풍속계 고도 변경 외에 나머지 비기후학적인 요인들(관측소 위치 변화, 관측 기기 변경 및 고장, 관측 간격 변화 등)을 고려하지 못했다는 한계가 있다.
따라서 이 연구는 Choi et al. (2021)과 같은 방식으로 물리적 보정을 수행하고 더 나아가 통계적 보정을 추가로 수행하였다. 이렇게 균질성을 확보한 자료를 바탕으로 한반도 지상 풍속의 장기 추세 및 추세의 변화를 추정하였다.
2. 자료 및 방법
2.1 자료
이 연구에서는 기상청 ASOS에서 관측된 1시간 간격의 지상 풍속 자료를 월 평균하여 사용하였다. 모든 관측소에서 풍속계 고도를 기록하기 시작한 1985년부터 2019년까지 분석하였다. 이 기간 동안 지상 풍속 자료에 결측이 없고, 관측 환경 기록에 오류가 없는 31개 지점 중에서 인근 관측소가 충분하지 않은 제주(184)와 성산(185) 지점을 제외한 총 29개 지점자료를 분석에 사용하였다. 또한 통계적 보정 과정에서 기준 자료로 사용된 인근 관측소 자료의 적합성을 확인하기 위해 재분석 자료를 추가적으로 이용하였다. 재분석 자료는 유럽중기예보센터(European Centre for Medium-Range Weather Forecasts, ECMWF)의 최신 재분석 자료인 ERA5 (ECMWF Reanalysis v5)의 수평 해상도가 0.25o × 0.25o인 10 m 고도의 풍속 자료를 이용하였다(Hersbach and Dee, 2016). 관측 환경 변경 기록으로 관측소 위치 및 해발고도 변화와 풍속계 고도 변경 정보는 기상 연보의 지상기상관측지점 일람표를 바탕으로 정리된 Choi et al. (2021)의 표를 참고하였다.
2.2 비균질성 보정(homogenization)
기존의 지상 풍속 자료를 OTS (Original Time Series)로 정의하고 비균질성 보정을 두 단계에 걸쳐 수행하였다. Figure 1은 이 연구에서 수행된 비균질성 보정 과정을 나타낸 모식도이다. 파란색은 물리적 보정 과정을 의미하고 이 과정을 거친 자료를 물리적 보정 자료(Physically-homogenized Time Series, PTS)로 정의하였다. 하늘색으로 표시한 PTS를 통계적으로 보정하는 과정을 거친 자료를 물리적 및 통계적 보정 자료(Physically and Statistically-homogenized Time Series, PSTS)로 정의하였다.
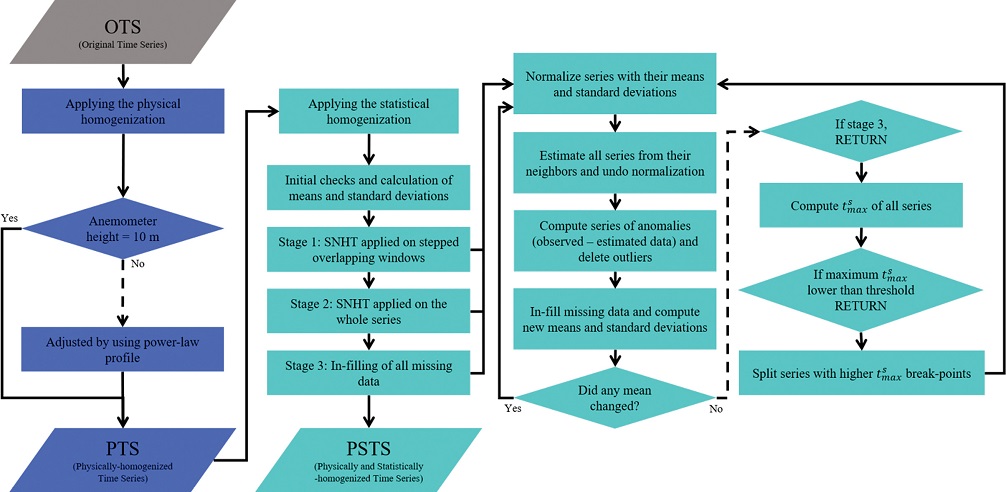
Flow-chart of the homogenization including physical homogenization (in blue) and statistical homogenization (in sky blue) in the Climatol package (Guijarro, 2018).
물리적 보정 과정으로 풍속계 고도 변경 정보를 바탕으로 고도에 따른 풍속의 지수 관계(Peterson and Hennessey Jr., 1978)를 이용하여 OTS를 10 m 고도의 풍속으로 보정하였다. 이 과정을 통해 풍속계 고도에 대한 균질성이 확보된 지상 풍속 자료인 PTS를 대상으로 통계적 보정을 수행하였다.
풍속계 고도 변화 이외의 비기후학적 변화는 통계적 보정을 통해 최소화하였다. 특히 Alexandersson (1986)의 SNHT 기법을 활용하였다. SNHT는 보정하려는 PTS와 비교 기준이 되는 자료(Reference Time Series, RTS)의 비율 또는 차이를 표준화하여, 표준화된 자료를 임의의 두 기간으로 나누었을 때 앞뒤 기간의 평균이 변화없이 표준정규분포를 따르는 지를 검증하는 방법이다.
여기서 RTS는 일반적으로 기후적인 특징을 공유하고 있는 인근 관측소 자료를 사용한다. 인근 관측소 자료가 PTS와 상관관계가 낮은 경우에는 재분석 자료, 수치모델자료, 또는 비슷한 특징을 갖는 다른 변수를 이용한다(Venema et al., 2018). 이 연구에서는 한반도 지상 풍속 자료에 대한 최적의 RTS를 선정하기 위해, 각 관측소 별로 가장 가까운 관측소 자료와 ERA5 자료를 고려하였다. 먼저 인근 관측소 자료로 구성한 RTS는 각 관측소에서 반경 60 km 이내의 관측소 자료를 역거리 가중 방법으로 평균한 것이다. 반경 이내에 관측소가 2개 미만인 경우, 반경 밖에서 거리, 지형, 상관계수를 고려해 관측소를 추가하고 최소 2개의 관측소 자료를 역거리 가중 방법으로 평균하여 RTS를 구성하였다. ERA5 자료로 RTS를 구성한 경우 각 관측소에서 가장 가까운 9개 격자 지점 자료를 역거리 가중 방법으로 평균하였다.
Figure 2은 두 종류의 RTS와 해당 PTS의 상관계수를 나타낸다. 인근 관측소로 구성한 RTS와 상관계수가 0.5 이상인 관측소는 전체의 약 72%(채색된 영역 중 0.5 이상)인 반면에 ERA5의 RTS와 상관계수가 0.5 이상인 관측소는 약 14%(검정 테두리 영역 중 0.5 이상)에 불과한 것으로 나타났다. Figure 3a는 자료로 RTS를 구성하는 것이 더 적합한 것을 의미하므로 이 연구에서는 관측 자료를 통계적 보정의 RTS로 활용하였다.
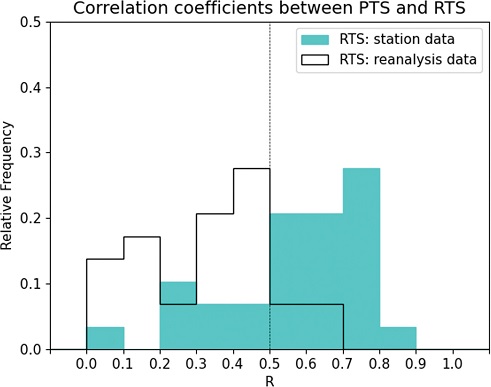
Relative frequency of the Pearson’s correlation coefficients between the physically homogenized time series (PTS) and its neighboring reference data (RTS) from station data (sky blue area) and ERA5 reanalysis data (black solid line).
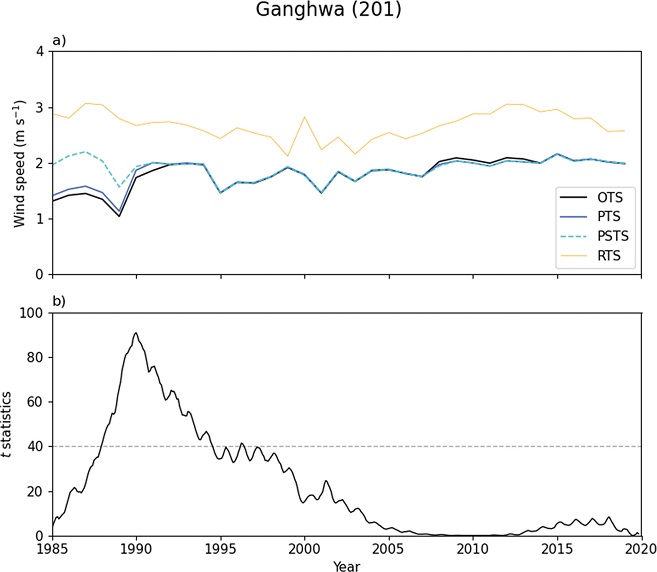
Time series of (a) annual-mean surface wind speed of original data (OTS; black solid line), physically homogenized data (PTS; blue solid line), and physically and statistically homogenized data (PSTS; sky blue dashed line) at Ganghwa (201) station and its neighboring reference data (RTS; yellow line). (b) The corresponding t statistics of the SNHT on monthly time scale. The grey dashed line denotes the threshold value for the break-point detection.
통계적 보정은 Climatol R 패키지(Guijarro, 2018; http://CRAN.R-project.org/package=climatol)를 이용해 수행하였다. 이 패키지를 사용하여 자료의 품질검정(quality control)과 SNHT를 이용한 통계적인 균질성 검정, 불연속점의 통계적 보정의 세 단계로 자료를 검정 및 보정하였다.
품질 검정 단계에서는 PTS에 존재하는 결측 또는 이상치를 확인한 다음, 가까운 시점과 거리에 위치한 RTS의 평균과 표준편차를 사용하여 결측을 추정하고, 보완된 PTS의 평균의 유효한 변화가 없을 때까지 반복 수행을 통해 결측을 추정하였다(Paulhus and Kohler, 1952).
SNHT 균질성 검정은 PTS에 나타나는 비균질한 지점을 찾아 균질화하는 과정으로 진행된다. PTS의 비균질 지점은 PTS와 RTS의 상대적인 차이를 표준화하여 탐지한다. i번째 월을 기준으로 RTS에 대한 PTS와 차이(Qi)는 식(1)과 같이 정의된다.
| (1) |
P는 PTS를 나타내고, R는 RTS를 나타낸다. 아래 첨자 i는 1985년부터 2019년까지 25년 동안 월 단위의 시간을 나타내며, N는 420(35년 × 12개월)에 해당한다. 와 는 각각 PTS와 RTS의 35년 평균을 의미한다.
특정 시점 b에서 PTS의 아노말리가 RTS의 아노말리보다 크다면, Qb가 상대적으로 증가하여 정규분포에서 벗어날 수 있다. 따라서 표준화된 Qi가 표준정규분포를 따른다는 것을 귀무가설 H0로 정하고, 기각하는 경우 시점 b는 불연속점으로 분류된다. 이에 대한 대립가설 H1은 시점 b를 기준으로 전후 기간의 평균이 각각 서로 다른 정규 분포를 따르는 것으로 가정한다.
가설 검정은 식(2)의 검정통계량 을 기준으로 수행하였다.
| (2) |
μ1과 μ2는 각각 {1, …, b} 시점의 표준화된 Qi의 평균과 {b + 1, …, N} 시점의 표준화된 Qi의 평균을 의미한다. b를 1부터 N - 1(= 419)까지 이동시키며 반복하여 시점 b를 기준으로 전후 기간에 대해 각각 t 검정 통계량을 N번 산출한다. 이렇게 반복적으로 산출된 N개의 t 검정 통계량 중 최대값이 정해진 임계값 보다 더 크면 귀무가설은 기각되며 b를 불연속점(break point)으로 탐지한다. 불연속점이 한번 발생하면 이를 기준으로 시계열을 나누어 전후 기간의 시계열에서 각각 위의 과정을 불연속점이 더 이상 나오지 않을 때까지 반복한다.
SNHT는 t 검정 통계량의 최대값을 가지고 하나의 시계열에서 단일 불연속점을 찾기 때문에 불연속점이 여러 개 있는 경우 이를 찾는데 한계가 있다. 이러한 문제를 줄이기 위해 Climatol은 전체 시계열을 1부터 N - m 시점까지 짧은 기간(m = 60)으로 나눈 시계열 조각에 대해서 반복적으로 SNHT 단계를 먼저 거친 다음, 시점 1부터 N(= 420)까지 전체 기간을 기준으로 SNHT 단계를 수행한다. 이 과정에서 탐지된 불연속점들을 기준으로 품질 검정 과정에서 결측값을 추정했던 방식으로 비균질성을 보정한다.
SNHT 단계에서 필요한 t 검정 통계량의 임계값은 Khaliq and Ouarda (2007)에서 제시되어 있으나, 이 값들은 몬테 카를로 시뮬레이션(Monte Carlo ideal simulation)을 통해 계산된 값으로 실제 사용된 변수나 시간 해상도에 따라 임계값과는 다를 수 있다. 임계값이 너무 작으면 불연속점이 과하게 발견되기 때문에 Climatol에서는 기본 설정된 값인 25로 먼저 보정을 수행한 다음, 결과로 제공되는 t 검정 통계량의 히스토그램을 참고하여 사용자가 임계값을 재설정하도록 제시하고 있다(Guijarro, 2018). 이 연구에서는 초기 Climatol 결과를 바탕으로 t 검정 통계량의 임계값을 40으로 설정하였다.
결과적으로 물리적 보정과 통계적 보정을 통해 균질성을 확보한 지상 풍속 자료(PSTS)를 대상으로 장기 추세를 분석하였다.
2.3 추세 변화 추정
물리적 및 통계적 보정을 거친 지상 풍속 자료(PSTS)의 장기 추세 변화를 단일 변화에 대한 선형회귀분석을 식(3)~(5)를 통해 추정하였다(Perron and Yabu, 2009; Kim and Son, 2020).
| (3) |
| (4) |
| (5) |
y는 분석 대상인 PSTS, t는 시간을 나타낸다. α와 β는 추세 변화점인 tB을 기준으로 전후의 추세를 결정하는 회귀계수로, t = 1부터 t = tB까지는 추세가 α로 추정되며, t = tB + 1부터 t = tmax까지는 α + β로 추정된 다. y0와 n(t)는 y 절편 및 회귀오차를 나타낸다. 이는 일반적인 선형회귀 식과 유사하나, 한번의 추세 변화를 dt 항으로 고려하는 방법이다. 즉, 최소 제곱법을 통해 추정된 α, β, tB가 최적의 추세 및 추세 변화점으로 산출된다.
산출된 추세 변화점의 통계적 유의성을 검증하는 일반적인 방법이 존재하지 않기 때문에 다음과 같은 방법을 사용하였다(Kim and Son, 2020). (1) 분석 대상 시계열이 회귀분석의 기본 전제인 오차의 정상성(stationary)을 만족하며, (2) 추정된 tB의 신뢰구간(Chang and Perron, 2018)이 분석 기간을 벗어나지 않아 tB가 신뢰구간 내에서 확실히 존재한다고 할 수 있을 때, 통계적으로 유의미한 추세 변화로 판별하였다. 오차의 정상성은 일반적으로 단위근 검정(unit root test)을 이용하여 확인할 수 있다. 그러나 이 연구에서는 추세 변화를 가정한 회귀분석 모형을 사용하였으므로, 한번의 추세 변화를 가정한 단위근 검정(Kim and Perron, 2009)을 사용하였다. 이 연구에서 해안 지역을 제외하고 내륙 지역과 한반도 평균 지상 풍속 자료는 모두 95% 유의수준에서 추세 변화를 고려한 정상성을 만족하였다.
3. 결 과
이 연구에서 수행한 보정 과정을 강화(201) 지점의 연평균 지상 풍속 자료를 통해 살펴보았다. Figure 3a는 강화(201) 지점의 보정 전(OTS; 검은 실선), 물리적 보정 후(PTS; 파란색 실선), 그리고 물리적 및 통계적 보정 후(PSTS; 하늘색 파선)의 연평균 지상 풍속 시계열을 나타낸다. 보정 전(OTS)과 물리적 보정(PTS)만 적용된 지상 풍속은 대체로 일치하나, 1990년대 중반 이전과 2000년대의 두 기간에서 차이가 드러난다. 관측 환경 변경 기록에 따르면, 강화(201) 지점은 풍속계 고도가 총 6번 변경되었는데, 그 중에서 1992년에 6.0 m에서 9.7 m로, 2008년에는 10 m에서 12 m로 변경되어 물리적 보정이 두드러진 기간과 대체로 일치한다.
또한 통계적 보정 과정에서 비교 기준이 되는 지상 풍속(RTS; 노란색 실선)과 PTS는 절대값의 차이가 있으나 전반적인 경년 변동성 및 장기 추세가 유사한 양상을 보였다. 해당 지점에서 RTS로 사용된 지점 자료는 서울(108)과 인천(112) 두 지점의 지상 풍속을 역거리 가중 평균하여 구한 것이다. 이렇게 구한 RTS를 활용하여 통계적 보정까지 거친 지상 풍속(PSTS)은 물리적 보정만 거친 지상 풍속(PTS)에 비해 보정 전 지상 풍속과의 차이가 크게 나타난다. 이는 물리적 보정만으로는 비기후학적인 요인에 의한 비균질성을 보정하는데 한계가 있음을 시사한다(Wan et al., 2010).
전체 시계열에 대해서 SNHT 과정을 수행하기 전, 시계열 조각들에 대한 반복적인 SNHT 과정에서는 강화(201) 지점의 유의미한 불연속점이 발견되지 않았다. Figure 3b는 강화(201) 지점의 전체 시계열에 대한 SNHT 과정에서 산출된 검정 통계량을 나타난 것이다. Figure 3b에서 점선으로 표시한 임계값인 40을 넘는 최대 검정 통계량이 1990년에 나타나 불연속점으로 탐지되었다. 탐지된 불연속점을 기준으로 시계열을 나누고 불연속점을 반복해서 탐지한 결과에서 강화(201) 지점의 지상 풍속 시계열에서 불연속점은 1990년에 한번 나타났다. 관측 환경 변경 기록을 확인한 결과 1990년에 발생한 25 m에서 46.4 m로의 해발고도 변경된 것으로 추정된다. 강화(201) 지점은 통계적 보정을 통해 물리적 보정(풍속계 고도 보정)에서 고려하지 못한 해발고도 변경에 따른 비균질성이 보정되었다고 볼 수 있다.
같은 방식으로 모든 관측소에서 물리적 보정과 통계적 보정을 수행하였다. 분석 기간 동안 풍속계 고도 변경이 없었던 대관령(100) 지점을 제외하고 모든 관측소에서 풍속계 고도 변경에 대한 물리적 보정이 수행되었다. 이를 바탕으로 통계적 보정까지 거친 결과를 보면 관측소에 따라 불연속점이 최소 0개[인천(112), 안동(136), 합천(285)]부터 최대 5개[거창(284)]까지 발견되었다. 총 29개 관측소에서 총 52개의 불연속점이 탐지되었다. 구체적으로 울산(152)의 경우 1998년과 2002년에 불연속점이 확인되었으며, 1998년은 해발고도가 31.5 m에서 34.7 m로 변경된 시기와 일치하였다. 또한 부여(236)는 불연속점이 1989년과 2000년, 2003년에 걸쳐서 확인되었다. 그 중 2000년은 해발고도가 16 m에서 11.3 m로 변경된 것과 일치하였다. 이처럼 실제 관측 환경 변경 시기와 일치하는 불연속점을 관측 환경 변경 기록을 바탕으로 확인한 결과 총 52개 중 21개로 나타났다. 이 불연속점들은 관측소 위치 변화, 해발고도 변화와 같은 비기후학적인 요인에 의한 것이고, 나머지는 기상 연보에 기록되지 않은 다른 비기후학적인 요인에 의한 것으로 추정된다.
이러한 물리적 및 통계적 보정이 지상 풍속의 장기 추세에 미치는 영향을 확인하고자, 보정 전후 지점별 연평균 지상 풍속의 장기 추세를 비교하였다(Fig. 4). 그림에서 채색된 막대는 t 검정(Student’s t-test) 결과 95% 유의수준에서 통계적으로 유의미한 장기 추세를 의미한다. 거의 모든 관측소에서 보정 전(OTS; 검은색 막대) 연평균 지상 풍속의 장기 추세는 물리적 보정을 거친 후(PTS; 파란색 막대) 전반적으로 약화되었다. 풍속계 고도 변경이 없었던 대관령(100)을 제외하고 28개 지점 중 22개 지점에서 장기 추세가 약화되었다. 이는 기존 OTS가 WMO에서 지정한 풍속계 표준 고도(10 m)에서 관측되지 않은 기간과 해당 고도로 변경된 기간 동안 발생한 비균질성 때문에 지상 풍속의 장기 추세를 과하게 추정하고 있었음을 나타낸다.
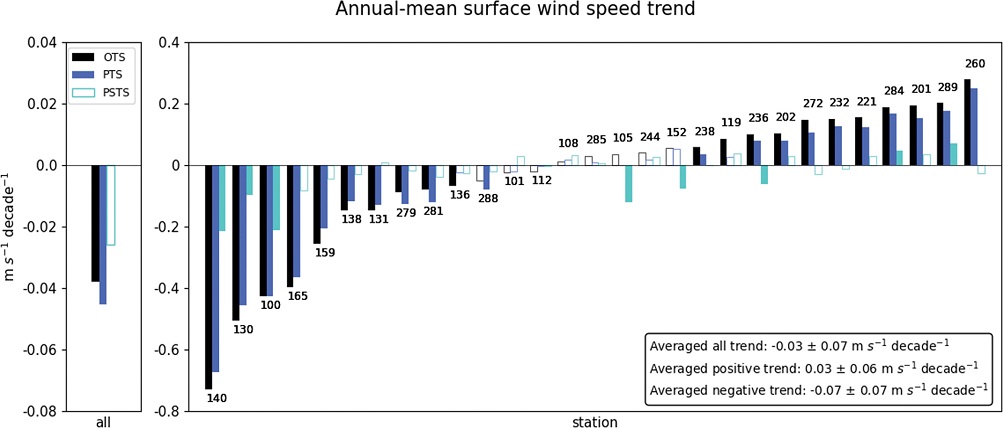
Linear trend of annual-mean surface wind speed from original (OTS; black), physically homogenized (PTS; blue), and physically and statistically homogenized data (PSTS; sky blue) at each station, with station number denoted at the tip of each bar. The filled bar represents the statistically significant trend at the 95% confidence level based on Student’s t-test. The average value of all 29 stations is shown in the left panel.
통계적 보정까지 거친 지상 풍속의 장기 추세(PSTS; 하늘색 막대)도 약화를 보였다. 20개 관측소에서 지상 풍속의 장기 추세가 약화되었는데, 그 중 9개 지점은 장기 추세가 약화되었을 뿐만 아니라 부호까지 달라졌다. 예를 들어, 울산(152)은 지상 풍속의 장기 추세가 0.05 (PTS)에서 -0.08 (PSTS) m s-1 decade-1으로 증가 추세가 뚜렷한 감소 추세로 뒤바뀐 것을 볼 수 있다. 또한 부여(236)는 장기 추세가 0.08 (PTS)에서 -0.06 (PSTS) m s-1 decade-1으로 바뀌었으며, 그 밖에 강릉(105)에서도 기존의 증가 추세에서 통계적으로 유의미한 감소 추세로 바뀌는 것으로 나타났다. 세 지점 모두 관측 환경 변경 기록과 일치하는 불연속점이 확인되었다.
결과적으로 물리적 보정과 통계적 보정을 통해 균질성이 확보된 지상 풍속(PSTS)은 총 29개 관측소 중에서 11개 지점에서 평균 0.03 ± 0.06 m s-1 decade-1의 증가 추세를 보였고, 18개 지점에서 평균 –0.07 ± 0.07 m s-1 decade-1의 감소 추세를 보였다. 종합적으로 한반도 평균 지상 풍속의 장기 추세는 -0.03 ± 0.07 m s-1 decade-1의 감소 추세를 보였다. 또한 평균에 비해 큰 표준편차가 확인되는데, 이는 지역에 따라 장기 추세가 민감하게 달라짐을 의미하며 전반적인 지상 풍속의 장기 추세는 통계적으로 유의미하지 않았다.
지상 풍속의 장기 추세는 지리적 분포에 따라 지역적으로 큰 차이를 보일 수 있다(McVicar et al., 2012). Figure 5는 각 관측소들의 지리적 분포를 나타낸다. Figure 5에서 볼 수 있듯이, 지상 풍속의 장기 추세가 내륙 지역에서는 일관되지 않았고, 지리산 부근의 거창(284), 산청(289)에서는 유의미한 증가 추세가 확인되었다. 반면, 해안에 위치하는 대부분의 지점에서 경기도 지역을 제외하고 통계적으로 유의미한 감소 추세를 보이는 특징을 보여 이는 해안 지역에서 풍속의 감소 추세가 더 뚜렷하다는 선행연구 결과와 일치한다(Seo et al., 2018).
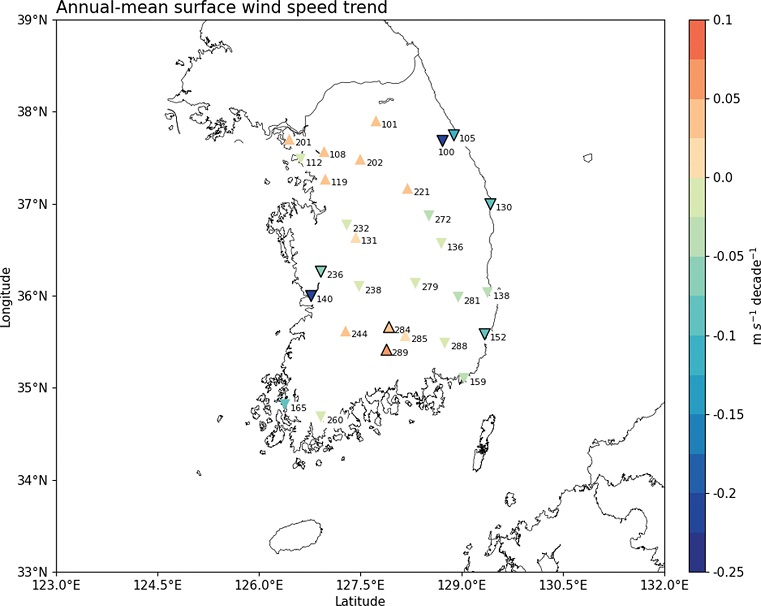
Linear trend of the physically and statistically homogenized (PSTS) surface wind speed for the period of 1985~2019. The warm-colored upward and cold-colored downward triangles denote the positive and negative trends, respectively. The black solid boundary represents the statistically significant trend at the 95% confidence level based on Student’s t-test.
한반도 지상 풍속의 변화가 통계적으로 유의미하지 않은 또다른 이유는 장기 추세에 급격한 변화가 존재하기 때문이다(Fig. 6). 기울기 변화를 고려한 선형회귀분석 기법을 적용하여 물리적 및 통계적 보정 후 지상 풍속(PSTS; 하늘색)의 장기 추세 변화를 추정한 결과, 2001년에 95% 신뢰수준에서 유의미한 추세 변화가 확인되었다. 2001년 이전까지 -0.10 m s-1 decade-1의 감소 추세를 보이다가 이후 기간에는 0.03 m s-1 decade-1의 증가 추세를 보였다. 이는 전지구 지상 풍속이 2000년대 이전까지 유의미하게 약해지는 추세를 보이다가 최근 다시 회복하고 있다는 선행연구와 일관된 결과이다(Azorin-Molina et al., 2018a; Zheng et al., 2019; Zhang and Wang, 2020). 이러한 감소 추세에서 증가 추세로의 변화가 보정 전 한반도 평균 지상 풍속(OTS; 검정색)에서는 나타나지 않았다.
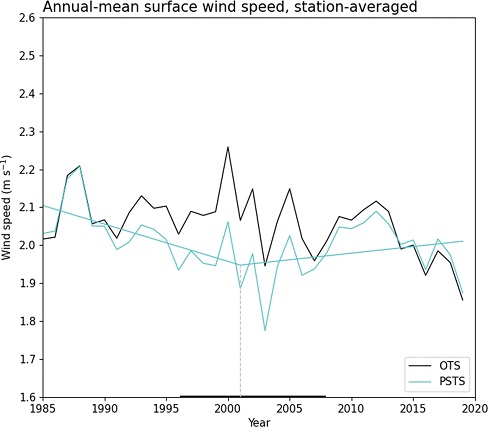
Time series of annual-mean surface wind speed from original (OTS; black), and physically and statistically homogenized (PSTS; sky blue) data averaged over all 29 stations. The sky-blue line represents the linear trends of the PSTS for the two sub-periods across the trend-changing point (grey dashed vertical line in 2001) with 95% confidence interval (black line in the x axis).
한반도 평균 지상 풍속의 추세 변화가 지역적으로 어떻게 나타나는지 확인하기 위해 해안 지역과 내륙지역으로 구분하여 추세 변화를 분석하였다. 해안과 내륙 지역 모두 지상 풍속의 장기 추세 변화가 2000년대 전후에 발생한 것으로 나타났으나, 해안 지역의 경우 통계적 유의성은 없었다. 해안 지역의 지상 풍속은 1996년을 기준으로 추세 변화가 확인되어 –0.25 m s-1 decade-1에서 0.00 m s-1 decade-1로 바뀌었다. 반면 내륙 지역의 지상 풍속은 2001년에 통계적으로 유의미한 추세 변화가 있었으며 이 시기를 기준으로 -0.06 m s-1 decade-1에서 0.04 m s-1 decade-1로 추세가 바뀌었다. 따라서 지상 풍속이 약해지고 있는 추세가 최근 다시 회복하고 있는 것이 한반도 평균 풍속뿐만 아니라 지역별로 나타나는 일관된 특성이라고 설명할 수 있다.
4. 요약 및 결론
이 연구에서는 물리적 및 통계적 보정을 통해 한반도 지상 풍속의 35년간(1985~2019) 장기 추세를 확인하였다. 물리적 보정은 관측 환경 변경 기록을 바탕으로 하여 10 m 풍속으로 변환하였다. 그 결과, 대관령(100)을 제외한 28개 관측소 중 22개 지점에서 기존 관측 자료의 추세보다 약화된 장기 추세를 보였다. 물리적 보정을 통해 비기후학적인 요인에 해당하는 풍속계 고도 변경이 기존 관측 자료의 장기 추세를 과대 추정하고 있음을 확인하였다.
물리적 보정 후에도 남아있을 수 있는 비균질성을 보정하기 위해 SNHT 방법을 이용하여 통계적 보정을 수행하였다. 그 결과, 29개 관측소에서 총 52개의불연속점이 발견되었고, 이 중 40%는 관측 환경 변경과 관련된 불연속점으로 확인되었다. 전체 관측소 중 69% 지점에서 물리적 보정만 거친 지상 풍속보다 통계적 보정까지 거친 지상 풍속이 약한 장기 추세를 보이는 것으로 나타났다. 특히 장기 추세의 크기만 바뀌었던 물리적 보정과는 다르게 통계적 보정의 경우 일부 지역에 걸쳐 장기 추세의 부호가 뒤바뀌는 경우도 확인되었다. 이는 장기 추세를 분석하는 과정에서 이러한 비균질성을 제거하는 절차가 정확한 장기 추세 판단에 중요하다는 것을 시사한다.
위의 과정을 거쳐 균질성이 확보된 지상 풍속의 장기 추세의 특성을 감소와 증가 추세를 띄는 지점을 나누어 살펴보았다. 먼저, 감소 추세를 보이는 지점은 전체 지점의 62%를 차지하며 평균적으로 -0.07 ± 0.07 m s-1 decade-1의 장기 추세를 보였고, 이 중 뚜렷한 감소 추세를 보인 지점들은 대부분 해안가를 중심으로 나타났다. 반면, 나머지 지점들은 0.03 ± 0.06 m s-1 decade-1의 증가 추세를 보였다. 또한 이처럼 평균 풍속이 비교적 큰 해안 지역에서 감소 추세가 뚜렷한 이유는 해안 지역에서 강풍 및 돌풍의 발생 빈도가 감소하기 때문이라고 알려진 바가 있다(Kim et al., 2020; Zhang and Wang, 2020). 향후 이러한 평균 풍속과 강도별 풍속 간의 관련성에 대한 추가 연구가 필요한 것으로 생각된다.
한반도 평균 풍속의 경우 2001년을 기준으로 통계적으로 유의미한 추세의 변화가 확인되었다. 이 시기를 전후로 -0.10 m s-1 decade-1의 감소 추세에서 0.03 m s-1 decade-1의 증가 추세로 바뀌었다. 이는 한반도에서도 지상 풍속이 약해지다가 최근 다시 회복하고 있는 전지구적인 지상 풍속의 장기 추세 변화(Azorin-Molina et al., 2018a; Zeng et al., 2019; Zhang and Wang, 2020)가 동일하게 나타나고 있음을 의미한다. 이러한 특징은 해안과 내륙 지역으로 나누었을 때에도 확인되었고 특히 내륙 지역에서 유의미하게 나타났다. 따라서 한반도 지상 풍속의 장기 변동성은 북반구 중위도 전역에 걸쳐 발생하는 대규모 순환 변동성(Azorin-Molina et al., 2018a; Zeng et al., 2019) 뿐만 아니라 국지적인 요인 또한 중요한 영향을 미친 것으로 보인다. 지상 풍속을 변화시키는 국지적인 요인으로는 도시화나 토지 이용 변화, 식생 성장 등에 의한 지표면 거칠기 변화를 꼽을 수 있다(Vautard et al., 2010; Wu et al., 2018).
최근 국제 사회에서는 기후변화 대응을 위해 여러 재생에너지 자원의 가용성에 대한 평가가 요구되고 있다. 그 일환으로 지상 풍속의 장기 추세는 풍력 발전 분야에서 필수적인 지표로 활용되기 때문에 비균질성 보정을 통해 지상 풍속 자료의 신뢰도를 확보하는 절차가 중요하다고 판단된다. 이 연구에서는 장기간 지상 풍속 관측 자료에 포함된 비기후학적인 요인에 의한 비균질성을 물리적 및 통계적으로 보정하여 선행연구와 일관된 지상 풍속의 장기 추세 변화를 정량화 하였다. 이를 통해 비균질성 보정을 통해 관측 자료 분석, 특히 수십년 규모의 추세 분석의 정확도를 향상시킬 수 있는 가능성을 제시하였다.
Acknowledgments
본 논문의 개선을 위해 좋은 의견을 제시해 주신 두 분의 심사위원께 감사를 드립니다. 이 연구는 2021년 해양수산부 재원으로 해양수산과학기술진흥원(과학기술기반 해역이용영향평가 기술개발, 20210427)의 지원을 받아 수행하였습니다.
References
-
Alexandersson, H., 1986: A homogeneity test applied to precipitation data. J. Climatol., 6, 661-675.
[https://doi.org/10.1002/joc.3370060607]

-
Azorin-Molina, C., S. Rehman, J. A. Guijarro, T. R. McVicar, L. Minola, D. Chen, and S. M. Vicente-Serrano, 2018a: Recent trends in wind speed across Saudi Arabia, 1978-2013: a break in the stilling. Int. J. Climatol., 38, e966-e984.
[https://doi.org/10.1002/joc.5423]

-
Azorin-Molina, C., C., J. Asin, T. R. McVicar, L. Minola, J. I. Lopez-Moreno, S. M. Vicente-Serrano, and D. Chen, 2018b: Evaluating anemometer drift: A statistical approach to correct biases in wind speed measurement. Atmos. Res., 203, 175-188.
[https://doi.org/10.1016/j.atmosres.2017.12.010]

-
Buishand, T. A., 1982: Some methods for testing the homogeneity of rainfall records. J. Hydrology, 58, 11-27.
[https://doi.org/10.1016/0022-1694(82)90066-X]

-
Chang, S. Y., and P. Perron, 2018: A comparison of alternative methods to construct confidence intervals for the estimate of a break date in linear regression models. Econom. Rev., 37, 577-601.
[https://doi.org/10.1080/07474938.2015.1122142]

-
Chen, X., S. Jeong, H. Park, J. Kim, and C.-R. Park, 2020: Urbanization has stronger impacts than regional climate change on wind stilling: a lesson from South Korea. Environ. Res. Lett., 15, 054016.
[https://doi.org/10.1088/1748-9326/ab7e51]

- Choi, Y.-J., C.-H. Park, S.-W. Son, J.-W. Lee, and D.-C. Hong, 2021: Long-term trend of surface wind speed in Korea: Anemometer height adjustment. Atmosphere, 31, 101-112, (in Korean with English abstract).
- Guijarro, J. A., 2018: Homogenization of climatic series with Climatol. Tech. Rep., State Meteorological Agency (AEMET), Balearic Islands Office, Spain, 20 pp.
- Hersbach, H., and D. Dee, 2016: ERA5 reanalysis is in production. ECMWF Newsletter, 147, 7.
-
Khaliq, M. N., and T. B. M. J. Ouarda, 2007: On the critical values of the standard normal homogeneity test (SNHT). Int. J. Climatol., 27, 681-687.
[https://doi.org/10.1002/joc.1438]

-
Kim, D., and P. Perron, 2009: Assessing the relative power of structural break tests using a framework based on the approximate Bahadur slope. J. Econom., 149, 26-51.
[https://doi.org/10.1016/j.jeconom.2008.10.010]

-
Kim, H.-J., and S.-W. Son, 2020: Recent Eurasian winter temperature change and its association with Arctic sea-ice loss. Polar Res., 39, 3363.
[https://doi.org/10.33265/polar.v39.3363]

- Kim, H. U., B. J. Kim, H.-G. Nam, J. H. Jung, and J.-K. Shim, 2020: Climatological spatio-temporal variation of strong wind in Korea. Atmosphere, 30, 47-57, (in Korean with English abstract).
-
Kim, J., and K. Paik, 2015: Recent recovery of surface wind speed after decadal decrease: a focus on South Korea. Climate Dyn., 45, 1699-1712.
[https://doi.org/10.1007/s00382-015-2546-9]

-
Martínez, M. D., C. Serra, A. Burgueño, and X. Lana, 2010: Time trends of daily maximum and minimum temperatures in Catalonia (ne Spain) for the period 1975-2004. Int. J. Climatol., 30, 267-290.
[https://doi.org/10.1002/joc.1884]

-
McVicar, T. R., and Coauthers, 2012: Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. J. Hydrol., 416, 182-205.
[https://doi.org/10.1016/j.jhydrol.2011.10.024]

-
Perron, P. and T. Yabu, 2009: Testing for shifts in trend with an integrated or stationary noise component. J. Bus. Econ. Stat., 27, 369-396.
[https://doi.org/10.1198/jbes.2009.07268]

-
Peterson, E. W., and J. P. Hennessey Jr., 1978: On the use of power laws for estimates of wind power potential. J. Appl. Meteorol., 17, 390-394.
[https://doi.org/10.1175/1520-0450(1978)017<0390:OTUOPL>2.0.CO;2]

-
Pettitt, A. N., 1979: A non-parametric approach to the change-point problem. J. Roy. Statist. Soc: Series C (Appl. Statist.), 28, 126-135.
[https://doi.org/10.2307/2346729]

-
Paulhus, J. L. H., and M. A. Kohler, 1952: Interpolation of missing precipitation records. Mon. Wea. Rev., 80, 129-133.
[https://doi.org/10.1175/1520-0493(1952)080<0129:IOMPR>2.0.CO;2]

-
Roderick, M. L., L. D. Rotstayn, G. D. Farquhar, and M. T. Hobbins, 2007: On the attribution of changing pan evaporation. Geophys. Res. Lett., 34, L17403.
[https://doi.org/10.1029/2007GL031166]

-
Seo, J., D.-S. R. Park, J. Y. Kim, D. Youn, Y. B. Lim, and Y. Kim, 2018: Effects of meteorology and emissions on urban air quality: a quantitative statistical approach to long-term records (1999~2016) in Seoul, South Korea. Atmos. Chem. Phys., 18, 16121-16137.
[https://doi.org/10.5194/acp-18-16121-2018]

-
Vautard, R., J. Cattiaux, P. Yiou, J.-N. Thépaut, and P. Ciais, 2010: Northern Hemisphere atmospheric stilling partly attributed to an increase in surface roughness. Nat. Geosci., 3, 756-761.
[https://doi.org/10.1038/ngeo979]

-
Venema, V., and Coauthors, 2018: Guidance on the homogenization of climate station data. EarthArXiv, 83 pp.
[https://doi.org/10.31223/OSF.IO/8QZRF]

-
Von Neumann, J., 1941: Distribution of the ratio of the mean square successive difference to the variance. Ann. Math. Statist., 12, 367-395.
[https://doi.org/10.1214/aoms/1177731677]

-
Wan, H., X. L. Wang, and V. R. Swail, 2010: Homogenization and trend analysis of Canadian near-surface wind speeds. J. Climate, 23, 1209-1225.
[https://doi.org/10.1175/2009JCLI3200.1]

-
Wu, J., J. Zha, D. Zhao, and Q. Yang, 2018: Changes in terrestrial near-surface wind speed and their possible causes: an overview. Climate Dyn., 51, 2039-2078.
[https://doi.org/10.1007/s00382-017-3997-y]

-
Zeng, Z., and Coauthors, 2019: A reversal in global terrestrial stilling and its implications for wind energy production. Nat. Clim. Change, 9, 979-985.
[https://doi.org/10.1038/s41558-019-0622-6]

-
Zhang, Z., and K. Wang, 2020: Stilling and recovery of the surface wind speed based on observation, reanalysis, and geostrophic wind theory over China from 1960 to 2017. J. Climate, 33, 3989-4008.
[https://doi.org/10.1175/JCLI-D-19-0281.1]
