기상청 기후예측시스템(GloSea5)의 과거기후장 앙상블 확대에 따른 예측성능 평가
Abstract
This study explores the optimal ensemble size to improve the prediction performance of the Korea Meteorological Administration's operational climate prediction system, global seasonal forecast system version 5 (GloSea5). The GloSea5 produces an ensemble of hindcast data using the stochastic kinetic energy backscattering version2 (SKEB2) and time-lagged ensemble. An experiment to increase the hindcast ensemble from 3 to 14 members for four initial dates was performed and the improvement and effect of the prediction performance considering Root Mean Square Error (RMSE), Anomaly Correlation Coefficient (ACC), ensemble spread, and Ratio of Predictable Components (RPC) were evaluated. As the ensemble size increased, the RMSE and ACC prediction performance improved and more significantly in the high variability area. In spread and RPC analysis, the prediction accuracy of the system improved as the ensemble size increased. The closer the initial date, the better the predictive performance. Results show that increasing the ensemble to an appropriate number considering the combination of initial times is efficient.
Keywords:
GloSea5, seasonal forecast, prediction performance, ensemble size1. 서 론
기상청 기후예측시스템(Global Seasonal forecast system version 5, GloSea5)은 전지구 기후모델인 HadGEM3 (Hadley Center Global Environmental Model Version 3)를 기반으로 개발된 앙상블 예측시스템으로 대기-해양-해빙-지면모델을 결합한 모델이다(MacLachlan et al., 2015). 앙상블 예측시스템은 기존 수치모델의 정보와 예측 과정의 불확실성에 대응하기 위한 방안으로 개발된 시스템으로서 모델의 서로 다른 초기조건들을 이용한 적분을 수행하여 단일 예측에 비해 향상된 예측성능을 제공한다.
일반적으로 수치모델의 예측성능은 모델의 모의 환경에 따라 매우 상이하다. 기상청 국립기상과학원에서는 기후예측시스템을 현업 운영 중에 있으며, 시스템의 예측성능을 높이기 위하여 예측시스템의 모의 환경 즉, 기후기간 연장, 초기화 기법, 앙상블의 수 및 생성 방법 등의 개선 방법들을 고안하고 있다(Hyun et al., 2020).
현재까지 전세계적으로 앙상블 예측시스템의 모의 환경 개선을 위한 여러 연구가 수행되어 왔다. 특히 앙상블 크기에 대한 연구는 시스템의 효율적인 운영과 예측성능 향상을 위하여 필수적인데(Kumar et al., 2001; Richardson, 2001; Müller et al., 2005; Scaife et al., 2014), 국외 연구에서는 Murphy (1988) 및 Brankovic et al. (1990)이 앙상블 수가 증가함에 따라 모델의 결정론적 오류가 감소한다는 것을 증명하였으며, Raynaud and Bouttier (2017)는 수평 해상도를 2.5 km에서 1.3 km로 증가시키는 것과 앙상블 수를 12개에서 34개로 증가시키는 것에 대한 이점을 비교한 결과, 앙상블 수의 증가가 해상도 증가보다 더 효과적임을 밝혔다. 또한, Talagrand et al. (1997)은 ECMWF의 예측 성능이 앙상블 크기가 약 20~30개에 이르면 완벽한 예측모델과 가까운 수준을 보임을 시사한 바 있으며, Weisheimer et al. (2019)은 ECMWF의 51개 앙상블 멤버와 110년의 기후기간에 대한 북대서양진동(North Atlantic Osciilation, NAO) 지수 모의성능을 산출한 결과, 작은 앙상블 크기의 경우 관측과의 상관관계가 낮음을 보였다.
국내 연구에서는 Ahn et al. (2018)이 부산대학교에서 자체 개발한 앙상블 예보 시스템의 40개 앙상블을 이용하여 멤버 수가 증가할수록 관측 기온과의 시간 상관계수 값이 증가했으며, 멤버의 수가 작을수록 어떤 앙상블 멤버를 선택하느냐에 따라 예측 성능의 차이가 매우 큼을 보였고, Kim (2019)은 ECMWF의 앙상블 예측을 이용하여 적절한 앙상블 크기 설정에 대한 연구를 수행한 바 있다. 또한 Hyun et al. (2020)은 기상청 기후예측시스템을 포함한 여러 타 기관의 예측시스템 결과를 이용하여 앙상블의 수, 초기 시간, 기후 모의 기간 등을 달리하여 확률예측 신뢰도를 산출하고, 계절 예측의 관점에서 영향을 평가한 바 있다.
이와 같이 앙상블 확대의 중요성이 많이 알려진 가운데 국내 현업 운영 중인 기후예측시스템의 앙상블 수에 대하여 중점으로 이루어진 연구는 거의 없다. 따라서 본 연구에서는 기상청 국립기상과학원에서 현업 운영하고 있는 기후예측시스템 과거기후장(hindcast) 앙상블의 확대 실험을 진행하였으며, 실험 결과를 이용하여 앙상블 수와 시간 지연을 이용한 앙상블 조합에 따른 민감도를 평가하고 현재 새 국가 기상 슈퍼컴퓨터 도입 시점에 맞추어 전산 환경이 확충되는 경우 현업 시스템에서의 앙상블의 수를 늘렸을 때의 최적의 앙상블 크기를 산정해 보고자 하였다.
2. 자료 및 분석방법
기상청 기후예측시스템은 추계적 운동에너지 후방 산란(Stochastic Kinetic Energy Backscattering version2, SKEB2; Bowler et al., 2009)과 시간 지연 앙상블(time-lagged ensemble)을 통하여 과거 기후장과 예측장(forecast)의 앙상블을 생산한다. SKEB2 기법은 모델 불확실성의 원인이 되는 누락된 동적 과정, 즉 모델 내부의 수평 확산과 이류과정에서 과도하게 소산되는 운동 에너지의 일부를 재도입하는 추계적 기법 중 하나이다. 현업 기후예측시스템의 예측장은 SKEB2 기법을 통해 한 초기 시간에 대하여 75일까지 2개, 240일까지 2개 총 4개의 앙상블이 생산되며, 과거 기후장은 한 초기 시간에 대하여 3개의 앙상블이 생산된다. 한편, 시간 지연 앙상블 기법은 서로 다른 초기 시간의 예측 자료를 조합하여 앙상블 수를 증가시키는 방법으로, 예측장에서는 7일간의 초기 시간으로 생산된 모델 결과를 합하여 60일까지의 예측장을 생산하는데 사용하는데, 이는 60일까지의 예측에 있어 7일간의 초기 시간 차이는 앙상블 예측을 위한 초기 변동성 범주 안에 들어 있는 것으로 생각하는 것이다. 또한 3주, 즉 21일간의 초기 시간으로 생산된 모델 결과를 합하여 6개월까지의 예측장을 생산하는데 사용하고 있다.
과거 기후장은 기후기간 동안 1, 9, 17, 25일의 초기 시간에 대하여 1개월, 6개월의 예측장을 생산한다. 매일이 아닌 1, 9, 17, 25일 4일에 대해서만 과거 기후장을 생산하는 이유는 수 십년의 기후기간 동안 매일의 초기 시간으로 앙상블을 생산하기에는 수가 너무 방대해짐에 따라 전산 자원이 감당하기 어렵고, 이 논문의 목적과 같게 처음 앙상블을 설정할 때의 전산 자원량과 앙상블 수, 예측성능 사이의 적정 값을 설정한 것이다. 이렇게 매월 4번 생산된 과거 기후 초기값은 현업에서의 예측 결과를 생산하는 일정에 맞추어야 할 경우는 1개월 예측의 경우 가까운 2개 초기값, 6개월 예측의 경우 가까운 4개 초기값에 가중치를 주는 방법으로 재생산하여 이용하고 있다.
현재 기상청 기후예측시스템의 기후기간은 1991~2016년까지 총 26년이나 본 연구에서는 기후기간에 속하는 1991∼2010년(총 20년)의 여름(6~8월 JJA) 및 겨울철(12~2월 DJF)에 대하여 과거 기후장의 앙상블 수를 3개에서 14개로 확대하는 실험을 수행하였다. 즉, 여름 및 겨울철에 대하여 4개의 초기 시간을 조합하여 현재 매달 12개 생산되는 앙상블을 총 56개의 앙상블로 확대 생산한 것으로, 이를 이용한 분석을 수행하였다. 이때 초기 시간은 여름철이 5월 9, 17, 25일과 6월 1일, 겨울철이 11월 9, 17, 25일과 12월 1일이다. 분석을 위하여 1개에서 56개의 앙상블 조합을 만들 때에는 최대 2000개의 무작위 조합을 중복되지 않게 추출을 하였으며, 각 조합들의 예측성능을 평가하고 평균값을 나타내었다.
분석에 이용된 자료는 현업 기후예측시스템의 1.5 m 기온, 해면기압, 500 hPa 지위고도, 강수량 예측 자료이며, 검증을 위하여 동일한 기간에 대한 관측 자료로 1.5 m 기온, 해면기압, 500 hPa 지위고도는 ECMWF ERA-interim 재분석자료(Dee et al., 2011)를, 강수량은 Global Precipitation Climatology Project (GPCP; Adler et al., 2003) 자료를 이용하였다. 예측성능 평가는 평균제곱근오차(Root Mean Squared Error, RMSE), 편차상관계수(Anomaly Correlation Coefficient, ACC), 스프레드(Spread), 예측가능요소비(Ratio of Predictable Components, RPC) 검증 지수를 통해 이루어졌다.
RMSE는 모델과 관측 값의 차이를 나타내는 척도로 본 연구에서는 bias correction은 되지 않은 모델과 관측의 절대값 검증을 위해 이용되었으며, RMSE가 0에 가까울수록 모델의 예측 값과 관측 값의 수치가 서로 유사하다고 평가된다[식(1)], ACC는 모델과 관측의 평년 편차 사이의 상관계수를 나타낸 것으로 1에 가까울수록 관측에서의 변동성을 모델이 잘 모의하였음을 의미한다[식(2)].
| (1) |
| (2) |
위의 식(1)과 식(2)에서 N은 분석기간으로 총 20년(1991~2010년)을, Fn, On은 각 연도의 모델과 관측의 값을 나타내고 , 는 분석기간 전체의 평년 값을 나타낸다.
스프레드는 앙상블 평균에 대한 각 멤버들의 표준편차로[식(3)], 신뢰도 높은 앙상블의 경우 앙상블 스프레드가 앙상블 에러의 크기를 알려주는 척도로써의 역할을 한다고 알려져 있다. 완벽한 앙상블 시스템에서는 스프레드의 크기가 RMSE 크기와 일치하며 이는 앙상블 편차가 예측의 오차를 적절히 표현함을 의미한다(Palmer et al., 2006; Rodwell and Doblas-Reyes, 2006). 따라서 스프레드가 너무 작으면 과신하는 예측(overconfident forecast)을, 너무 크면 신뢰도가 낮고 불확실성이 큰 과소 예측(underconfident forecast)을 나타낸다. 한편, RPC는 계절내-수년 규모에서 예측가능한 요소(Predictable Components, PC)의 예측성능을 평가하는 방법으로 PC를 예측할 수 있는 총 분산에 대한 비의 제곱근 즉, signal-to-noise ratio로 정의하고 관측의 PC (PCobs)와 모델의 PC (PCmdl)의 비로 계산한다. 하지만, 관측의 signal-to-noise ratio는 직접적으로 알 수 없기 때문에 상관계수의 제곱(r2)이 모델에 의해 설명되는 관측의 변동성을 반영한다는 사실을 이용하여 모델의 signal-to-noise ratio 대비 관측과의 상관계수(r)의 비로 계산하며(Eade et al., 2014; Dunstone et al., 2020; Smith et al., 2020), 이상적으로 RPC가 1의 값을 가질 때 모델이 완벽한 예측성능을 갖는다[식(4)]. RPC가 1보다 작은 경우는 앙상블 멤버들은 서로 잘 맞지만 모델이 관측의 변동성을 잘 모의하지 못하는 ‘과신하는 예측’을 의미하며, RPC가 1보다 큰 경우는 모델이 관측의 변동성을 잘 모의하지만 앙상블 멤버들이 서로 잘 맞지 않는 ‘과소 예측’ 상태를 의미한다.
| (3) |
| (4) |
식(3)에서 M은 앙상블 멤버 수, , fmn는 각각 해당 연도의 앙상블 평균 값과 m번째 앙상블 멤버의 예측값을 의미하고 식(4)에서 r은 모델과 관측 사이의 상관계수, 는 앙상블 평균의 분산, 은 개별 멤버들의 평균 분산을 의미한다.
본 연구의 주 목적인 최적 앙상블 수를 선정하기 위한 방법으로 최소-최대 정규화(Min-Max Normalization) 방법을 이용한 정규화된 ACC를 산출하였다. 이는 앙상블 멤버의 개수가 최소일 경우의 ACC를 0, 최대일 경우의 ACC를 1로 두고 나머지 값들은 비율을 맞춰서 0에서 1 사이의 값으로 스케일링해주는 방법이다. 예를 들어, 앙상블 개수 x의 ACC를 X라고 할 때 이 값을 정규화시키면 (X-MIN)/(MAX-MIN)의 값을 가지게 되며, 정규화된 ACC가 빠르게 1로 포화 될수록 적은 앙상블 개수로도 높은 예측성능을 나타낼 수 있음을 의미하므로 앙상블 민감도가 작다고 평가될 수 있다.
3. 결 과
3.1 앙상블 확대에 따른 예측성능 평가
앙상블 확대에 따른 예측성능 평가에 앞서, 추계적 기법(SKEB2)과 시간 지연(Time-lagged)에 따른 앙상블의 생성 범위가 어느 정도의 변동성 범위 안에 드는지, 약 한달 전의 초기 시간을 이용하는 시간 지연 기법이 추계적 기법의 앙상블 스프레드 범위 안에 드는지에 대한 앙상블 생성 기법의 적정성을 확인해 보았다. Figure 1은 전지구 영역의 20년 평균 추계적 및 시간 지연 기법에 따른 앙상블 범위 즉 스프레드를 나타낸 그림이다(강수량 그림 제외). 그 결과, 앙상블 분포는 추계적 기법이 시간 지연에 비해 1.15~2.12배 가량 큰 범위를 갖는 것으로 나타났다. 다만 매년 가장 빠른 9일 초기 시간(5월 9일과 11월 9일)과 가장 늦은 1일의 초기 시간(6월 1일과 12월 1일)의 스프레드를 비교해 보았을 때에는 한달 사이에 특히 기압장에서 스프레드의 변동이 크게 나타나고 있으며(그림 제외), 이 초기 시간에 따른 예측 성능에 대해서는 이후 3.3절에서 살펴 보았다.
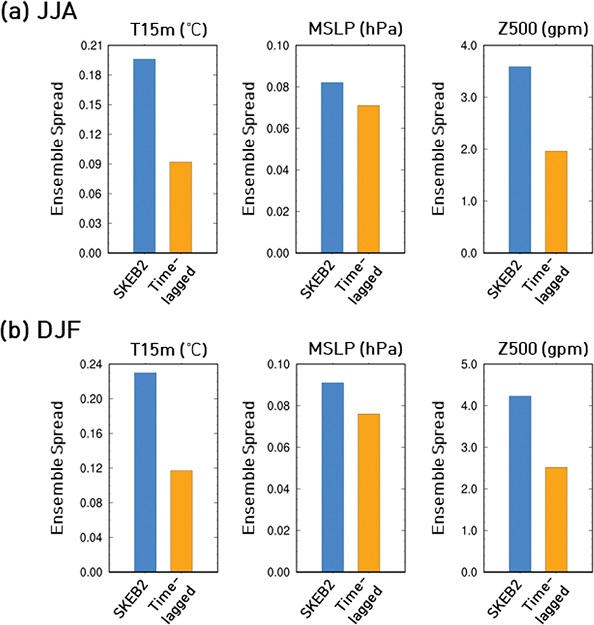
Comparison of ensemble spread produced by stochastic kinetic energy backscattering version2 (SKEB2) and time-lagged ensemble. The blue and orange bar indicates SKEB2 and time-lagged ensemble spread, for (a) JJA and (b) DJF during hindcast period (1991~2010).
기후예측시스템의 앙상블 확대에 따른 예측성능을 평가하기 위하여 앙상블 확대 실험을 통해 생산된 총 56개 앙상블을 이용한 검증결과를 현업 앙상블 수(12개)의 결과와 비교 분석하였다(무작위 2000개 조합). Figure 2는 전지구(극지역 제외, 60oS~80oN) 및 위도별(저위도, 중위도, 고위도) 앙상블 수에 따른 RMSE, ACC 예측성능을 나타낸다. 여기서 저위도는 양 반구의 위도 0o~30o, 중위도는 30o~60o, 고위도는 60o~90o에 해당하는 영역 평균한 값이며, Fig. 2의 OPER, EXP라고 표기된 부분이 각각 현업시스템과 확대 실험의 결과이다. 현업시스템에서의 현재 기후장에 대한 앙상블 수는 56개 앙상블을 모두 이용했을 때에 비해 RMSE와 ACC가 각각 평균 72%, 86% 예측성능에 이르고 있었다. 그러나 개별 변수와 영역을 따로 보았을 경우에는 고위도 영역 기압장 등에서 앙상블 확대에 따른 개선의 여지가 많이 남아 있는 것을 알 수 있었다. 검증지수별로 살펴보면 모든 변수의 RMSE는 앙상블 멤버 수가 증가함에 따라 급격하게 감소하였다가 감소율은 둔화되지만 계속해서 감소함을 보였다. 예를 들어 전지구 영역에서 RMSE는 모든 변수에 대하여 현업 앙상블 수(12개)에 비해 56개를 모두 이용했을 때 여름과 겨울철에 각각 약 14.3%, 14.6% 감소하는 효과를 보였다.
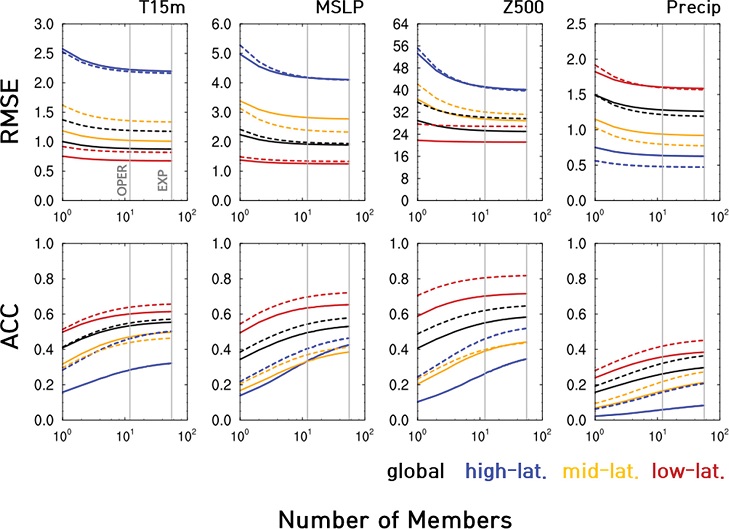
RMSE (top) and ACC (bottom) by ensemble size over global, high-, mid-, and low-latitude. The solid and dashed lines represent JJA and DJF, respectively. (OPER: 12-member, EXP: 56-member).
Figure 2에서 위도별 RMSE는 강수량을 제외한 모든 변수들이 고위도에서 가장 크고 저위도로 갈수록 작음을 알 수 있으며, 강수량의 경우는 반대로 저위도에서 가장 크고 고위도로 갈수록 작아졌다. ACC는 모든 변수들이 저위도가 가장 크고 고위도가 가장 낮았는데, 이는 주된 기후 예측의 소스로 생각되는 적도에서 기온, 기압 변수들의 예측성능이 크지만, 적도에서 변동폭이 큰 강수량의 경우는 저위도 ACC가 높지만 그만큼 오차도 큰 이유이다. 한편, RMSE와 ACC 관점에서의 앙상블 확대 효과는 기온, 기압 변수는 고위도에서, 강수량은 저위도에서 가장 크게 나타났다. 즉, 앙상블의 개선 효과는 변동성이 큰 영역에서 큰 것을 알 수 있었다.
계절별 현업대비 ACC는 전지구 영역에서 여름과 겨울철에 각각 약 28.7%, 26.7% 증가하는 효과를 보였다. 변수별로는 현업 대비 앙상블 개선 효과가 고위도 강수량에서 최대 약 44.9%로 가장 컸으며, 다음으로 고위도 500 hPa 지위고도에서 40.1%의 개선율을 보였다. 전체적으로 중-고위도 강수량에서의 개선율이 가장 컸으며(특히 여름철), 다음으로 500 hPa 지위고도와 해면기압의 개선율이 크고, 1.5 m 기온의 개선율은 가장 작았는데, 강수량의 경우 예측성능 개선율이 가장 컸으나 56개의 앙상블로 확대하였을 때에도 ACC가 0.5 미만의 통계적으로 유의하지 않은 수준으로 나타나 본 분석에 대한 해석에 주의가 필요하다. 한편, 동아시아에서의 여름과 겨울철의 ACC는 현업 대비 각각 28.9%, 25.7% 증가하는 효과를 보였다(그림 제외).
Figure 3은 56개 앙상블과 12개 앙상블의 RMSE, ACC 예측성능 차이를 공간분포로 나타낸 것이다. 이 분석에서는 Fig. 2에서 전지구 영역을 기준으로 RMSE와 ACC의 개선율이 가장 높은 해면기압 및 강수량에 대하여 이루어졌다. 분석 결과, 해면기압의 RMSE는 여름과 겨울철에 각각 남극과 북극 부근에서 가장 크게 개선되었는데, 극 소용돌이 등에 의한 변동성이 강한 영역에서 앙상블이 증가할수록 오차를 많이 감소시킬 수 있음을 알 수 있다. 그리고 ACC는 여름철의 북아시아, 겨울철의 그린랜드와 북미 지역, 알류산 저기압 지역 등이 포함된 고위도에서 가장 크게 개선되었다. 강수량은 RMSE 관점에서 열대와 아열대 강수대를 따라 현저한 개선 효과를 보였으나, ACC는 열대태평양에서 가장 작고 나머지 영역에 대해서는 뚜렷한 특징을 보이지 않았다.
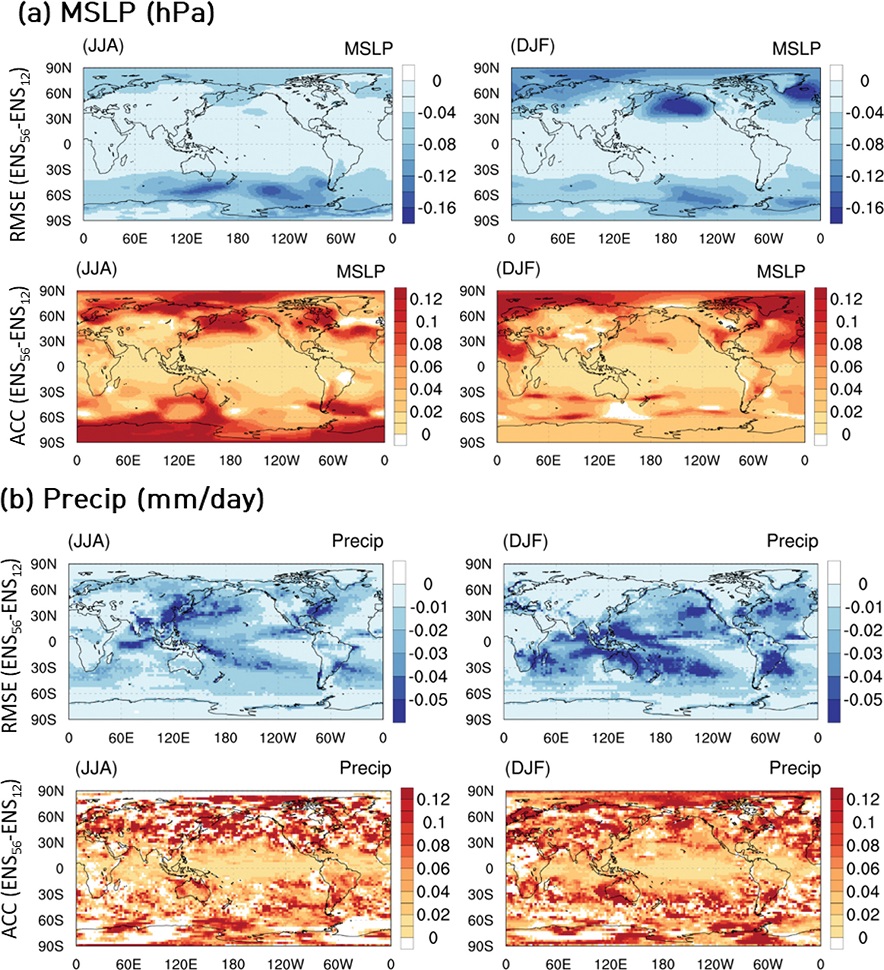
Improvements of (a) MSLP and (b) precipitation according to the ensemble expansion from 12 to 56 members. Left panel is for JJA and right is DJF (Top panel: RMSE, Bottom panel: ACC).
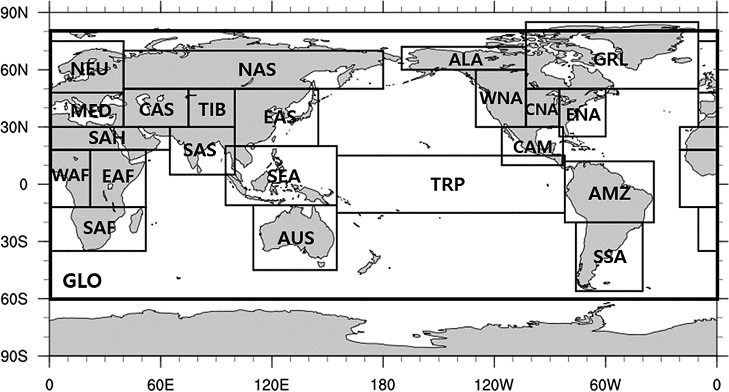
앙상블 확대의 영향을 영역별로 좀 더 세분화 하여 살펴보고 최적의 앙상블 크기를 산정하기 위하여 기준 선행연구 Giorgi and Francisco (2000)의 분석 영역(Fig. 4)을 참고하여 총 23곳의 영역을 선정한 후각 영역에 대한 정규화된 ACC를 산출하고(Fig. 5), 앙상블의 개선 효과가 변동성이 큰 영역에서 스프레드의 증가로 인한 것인지를 확인해 보고자 각 영역별 앙상블 스프레드와 비교하였다(Fig. 6).
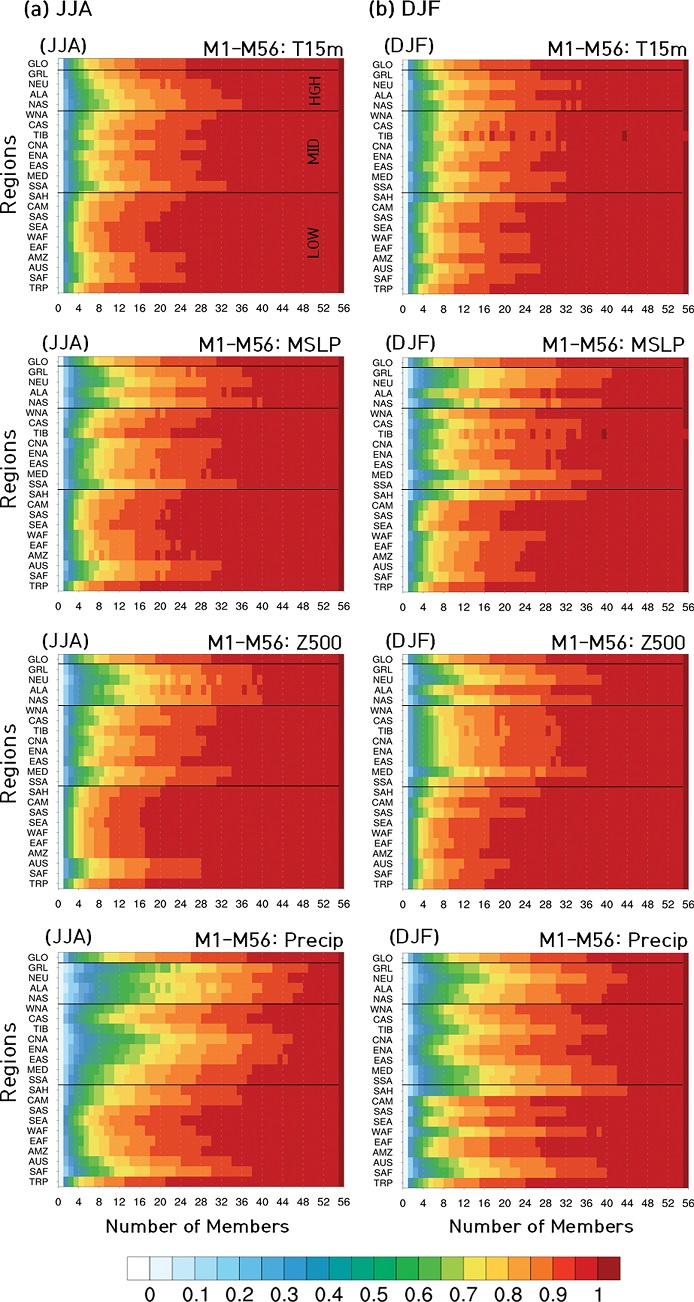
Normalized ACC by regions in Fig. 4 as ensemble size increases during (a) JJA and (b) DJF (HGH: high-latitude, MID: mid-latitude, LOW: low-latitude).
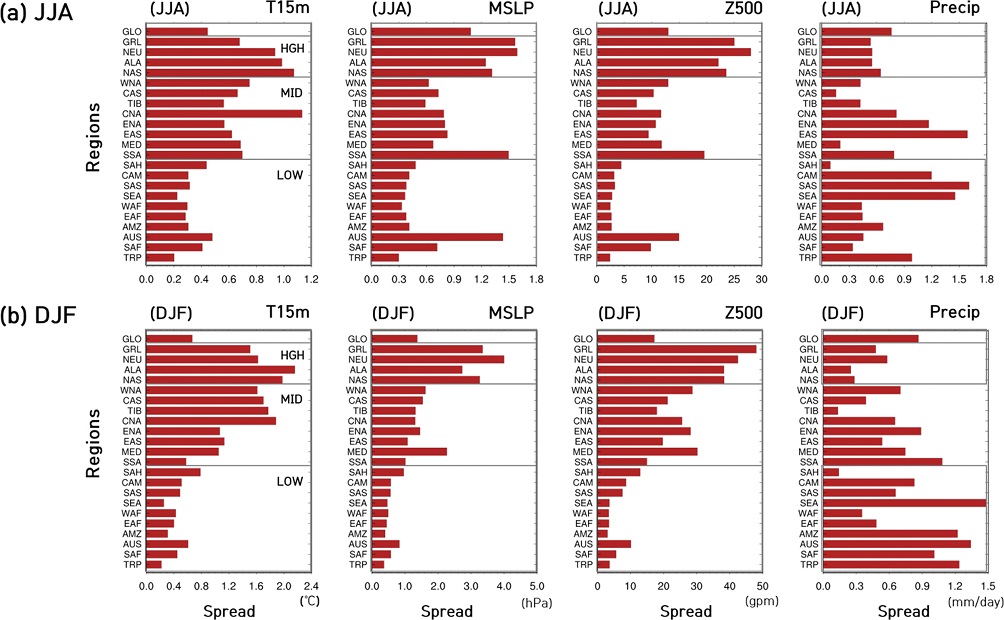
Ensemble spreads by regions in Fig. 4 during (a) JJA and (b) DJF (HGH: high-latitude, MID: mid-latitude, LOW: low-latitude).
Figure 5는 여름과 겨울철의 각 영역에서 정규화된 ACC를 산출한 것이다. 이 분석에서는 최소-최대 정규화(Min-Max Normalization) 방법을 이용하였으며 정규화된 ACC가 빠르게 포화 될수록 앙상블 민감도가 작은 영역이라고 평가될 수 있다. 앞서 Fig. 2에서 살펴본 것과 마찬가지로 다른 변수들에 비해 강수량의 앙상블 민감도가 가장 크게 나타나 앙상블 확대에 따른 예측성능 개선 효과가 가장 큰 것을 알 수 있었다. 또한, 모든 변수는 그린란드(GRL), 북유럽(NEU), 북아시아(NAS) 등이 속하는 고위도에서 앙상블 민감도가 크고 열대태평양(TRP)을 포함한 저위도 영역에서 작음을 보였다. Table 1은 Fig. 5 결과를 바탕으로 전지구, 동아시아, 열대 태평양 영역에서 정규화된 ACC가 포화되기 시작할 때의 앙상블 개수를 나타낸 것이다. 전지구 영역(GLO)과 중위도에 속하는 동아시아 영역(EAS)은 강수량을 제외한 변수들이 25 ~32개, 강수량은 37~44개의 범위에서 포화되어 현업 앙상블 수에 비해 많은 앙상블을 필요로 하는 것으로 나타났다. 한편, 23개 영역 중 가장 작은 민감도를 나타낸 TRP에서는 강수량을 제외한 변수들이 17~18개, 강수량은 22~25개 앙상블에서 포화되었다.
앙상블 민감도와 각 영역별 앙상블 스프레드를 비교해 보았을 때(Fig. 6), 대부분의 변수들이 민감도가 큰 영역에서 스프레드 또한 크게 나타났으나 강수량은 영역별 스프레드와 정규화된 ACC가 다른 변수에 비해 관련이 낮게 분포하는 것을 볼 수 있었다. 정규화된 ACC가 0.95 이상의 값을 나타내는 앙상블 수를 기준으로 영역별 스프레드와의 상관계수(R)를 산출해 본 결과, 여름철의 1.5 m 기온, 해면기압, 500 hPa 지위고도가 각각 0.86, 0.91, 0.83, 겨울철은 각각 0.72, 0.77, 0.86으로 강한 상관을 보인 반면, 강수량은 여름철과 겨울철 모두 0.5 미만의 약한 상관을 보였다. 이와 관련하여 선행연구에서는 모델의 예측성능을 키우기 위해 스프레드를 키워야 하며, 스프레드를 키우는 방법으로 앙상블 수를 늘린 바 있다(Williams et al., 2013).
3.2 앙상블 스프레드 평가
앙상블 예측시스템에 있어서 앙상블 평균과 관측 사이의 예측성능뿐만 아니라 시스템 자체의 앙상블 스프레드 평가 또한 중요하다(Corti et al., 2012; Goddard et al., 2012). 앞선 2장에서 설명했듯이 앙상블 RPC와 스프레드는 앙상블 시스템의 과신(overconfidence)과 과소(underconfidence)를 평가하는데 이용되므로(Eade et al., 2014; Baker et al., 2018), 본 파트에서는 RPC와 스프레드를 이용한 분석을 진행하였다. Figure 7은 전지구 영역에서의 RPC를 RPC 계산식에서 분자 및 분모에 해당하는 상관계수 및 signal-to-noise ratio(SNR)와 함께 나타낸 것으로, RPC는 앙상블 수의 확대에 따라 증가하였으며, 강수량을 제외한 대부분의 변수에 대하여 계절 간 차이가 크지 않았다. 해면기압과 500 hPa 고도장에서의 RPC는 앙상블을 확대할수록 완벽한 예측성능을 의미하는 1에 가까운 값을 보이고 있었지만, 1.5 m 기온과 강수량의 경우는 1보다 작은 값 즉, ‘과신하는 예측’을 보이고 앙상블 수를 56개로 확대한 결과 비교적 1과 가까운 값을 갖게 되었다.
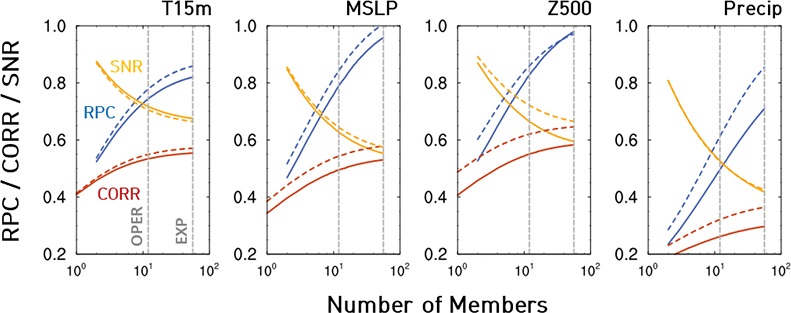
Ratio of Predictable Components (RPC), Correlation (CORR), and Signal-to-Noise Ratio (SNR) as a function of ensemble size for global mean. Solid and dashed lines represent JJA and DJF, respectively.
RPC와 함께 상관계수, signal-to-noise ratio (SNR)를 살펴본 결과(Fig. 7), 앙상블 확대에 따라 상관계수는 증가하고 SNR은 감소함을 보였다. 앙상블 수가 증가하면서 노이즈가 증가하여 SNR이 감소되는 것으로 확인하였으며(not shown), 앙상블 확대에 따라 각 지수들이 증가/감소하는 변화율을 보면, 상관계수가 작은 증가를 보여도 SNR이 급격하게 감소함에 따라 RPC 값이 급격한 증가를 보임을 알 수 있다. 이는 상관계수보다 SNR이 RPC에 더 큰 영향을 준 것으로 보여지며, 이러한 효과는 해면기압에서 가장 작고 강수에서 가장 크게 나타났다. 한편, 해면기압은 앙상블 멤버를 56개로 증가시킴에 따라 완벽한 값을 나타내는 1에 가까워짐을 확인하였으며, 강수량은 다른 변수에 비해 RPC 관점에서 더 개선될 여지가 있음을 확인할 수 있었다.
모델이 적절한 수준의 스프레드를 가지는지 평가하는 방법으로는 앙상블 평균의 RMSE와 전체 앙상블 스프레드를 비교하는 방법이 있다(Strommen and Palmer, 2019). Figure 8은 전지구 영역(극 제외)에 대한 앙상블 수에 따른 RMSE 및 스프레드의 산포도로 이상적으로는 RMSE와 스프레드 값이 같아 기울기가 1인 기준선에 닿아야 한다(Palmer et al., 2006; Rodwell and Doblas-Reyes, 2006). 분석 결과, 앙상블 수가 증가할수록 RMSE는 감소하고 스프레드는 증가함에 따라 기준선과 가까워짐을 확인할 수 있었으나 RMSE에 비해 스프레드가 과소모의되어 기준선에 미치지 못하는 모습을 보였다. 변수 별로 살펴보면, 1.5 m 기온과 500 hPa 지위고도의 RMSE 대비 스프레드는 앙상블 멤버 56개를 이용했을 때의 여름철에 51~52%, 겨울철에 57~58%, 해면기압이 각각 57%와 71%, 그리고 강수량이 각각 60%와 73%의 수준을 보였다. 한편, 현재 결과에서 앙상블 증가에 따른 RMSE와 스프레드의 비의 변화가 선형적으로 이루어진다고 가정했을 때 그 비율이 1에 포화되려면 훨씬 많은 앙상블이 필요할 것으로 예상된다. 하지만 단순히 앙상블 수의 확대가 아닌 초기 시간 조합을 달리하는 등 더욱 좋은 예측성능을 이끌어내는 앙상블 생성 방안을 찾는다면 비교적 적은 개수로 앙상블 수를 증가시켜도 RMSE와 스프레드 비율이 1이 되는 결과를 보일 수 있을 것이라 생각된다.
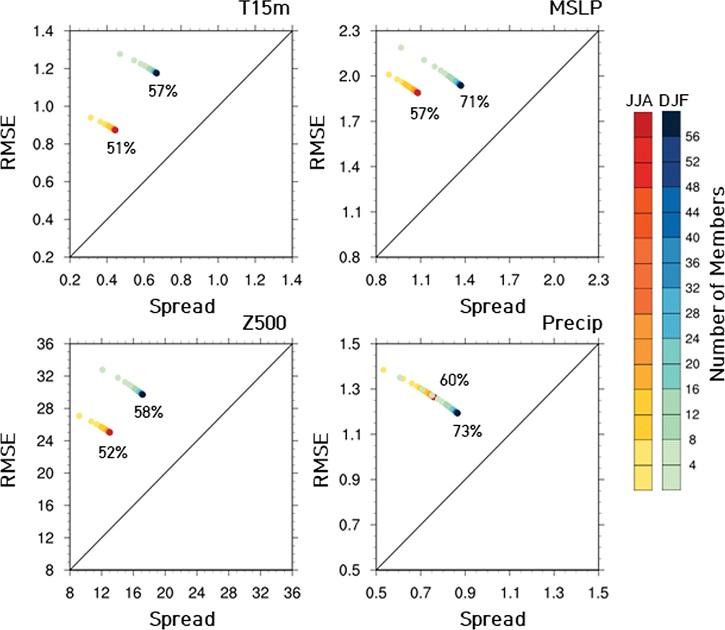
The relationship between RMSE and ensemble spread as a function of ensemble size for global mean. Solid line represents results of a ‘perfect’ model. Values shown in the plots are the ratio of ensemble spread to RMSE (%).
RMSE에 비해 스프레드가 과소모의되는 결과 또한 RPC 분석에서 보였던 ‘과신하는 예측’의 결과이다. 계절예측에서의 ‘과신하는 예측’은 잘 알려져 있으며(Weisheimer et al., 2019), 이와 관련하여 Vitart (2017)은 MJO에 대한 S2S 모델들(ECMWF, NCEP, 그리고 BoM)이 모두 ‘과신하는 예측’을 보이며, 앙상블 스프레드가 RMSE에 비해 매우 작은 값을 나타냈다고 밝혔으며, Weisheimer at al. (2019)은 NAO에 대한 앙상블 및 기후기간의 크기가 RMSE와 스프레드의 비에 미치는 영향을 분석한 결과, RMSE와 스프레드의 비는 적은 앙상블 수에서 과대모의됐으며, 앙상블 수가 증가함에 따라 점차 1에 가까운 값을 보인 바 있다.
3.3 초기 시간에 따른 예측성능
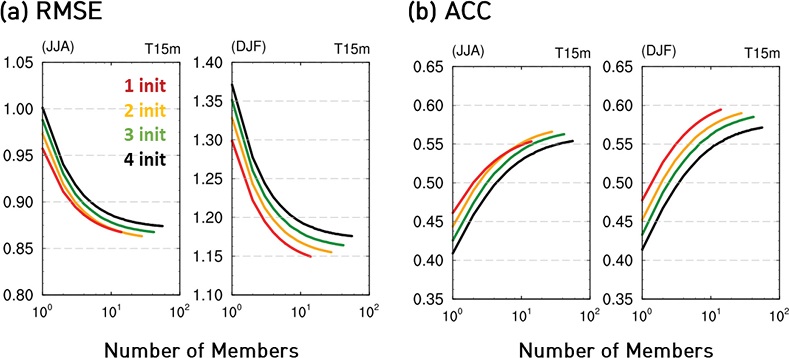
본 연구에서는 하나의 초기 시간당 생산하는 앙상블을 확대하였기 때문에 가까운 초기 시간만을 가지고 앙상블 평균을 함으로써 계절내 예측 기간에서의 예측성능을 개선시킬 수도 있다. 따라서 앙상블 확대 효과뿐만 아니라 초기 시간별 예측성능을 살펴보고 초기 시간의 수/조합이 예측성능에 어떠한 영향을 미치는지 살펴보고자 하였다. 이 분석에서는 앞선 앙상블 확대실험 결과인 14개의 앙상블을 모두 이용하였으며, 전지구 영역을 분석 영역으로 선정하였고 각 초기 시간에 대한 예측성능을 모든 초기 시간을 이용한 경우(총 56개)와 비교 분석하였다. 이 분석에서는 모든 변수에서 비슷한 결과가 나타나 1.5 m 기온만을 보였다. 먼저, RMSE는 여름철과 겨울철 모두 예측 시간(forecast time)이 짧을수록 즉, 타겟 계절과 초기 시간이 가까워질수록 감소하며, ACC는 증가함을 보였다(Fig. 9). 모든 초기 시간을 고려한 경우(총 56개 앙상블, 검은색) 보다 가장 가까운 초기 시간인 여름철 6월 1일과 겨울철 12월 1일의 앙상블 만을 사용한 것이 더 나은 예측성능을 보였으며, 그 다음 25일 초기 시간을 쓴 경우 모든 초기 시간을 다 쓴 경우와 비교했을 때 조금 낮은 성능을 보였다.
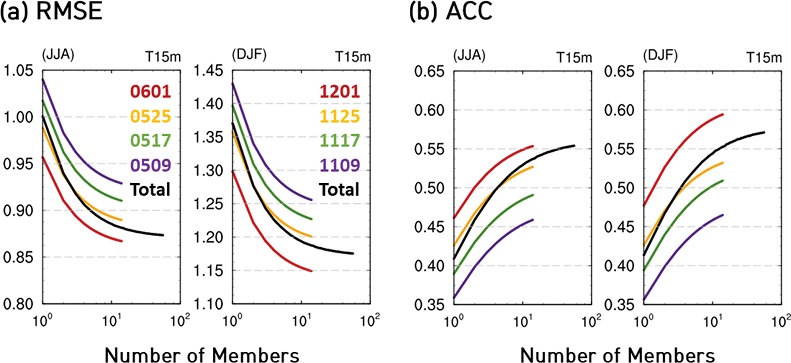
(a) RMSE and (b) ACC of 1.5 m temperature as a function of ensemble size for each initial time. Black line shows the result using all initial dates and each color represents each initial time.
앞서 Fig. 9에서 가장 가까운 초기 시간을 사용하였을 경우 가장 예측성능이 좋음을 보였음으로, 타겟 계절을 기준으로 가장 가까운 1개 초기 시간부터 차례로 4개 날짜까지의 초기 시간(각각 1~4 Init)을 늘려갔을 때 예측성능을 산출하였다(Fig. 10). ACC는 대부분 가까운 2개의 날짜를 이용하였을 때 가장 큰 값을 보인 반면, RMSE는 500 hPa 지위고도의 경우 가장 가까운 초기 시간 1개 날짜만을 이용했을 때 가장 좋았고, 1.5 m 기온은 가까운 1~2개 날짜, 해면기압과 강수량은 2~3개 날짜를 이용했을 때 가장 낮았다. RMSE와 ACC 관점에서 모든 초기 시간을 이용한 경우(4 Init)의 예측성능이 대부분 가장 좋지 않게 모의되었는데 이러한 검증 결과로 보아 앙상블을 무조건 늘리는 것 보다는 전산 자원량을 확보하고 초기 시간의 조합을 고려하여 적정 개수로 앙상블을 늘리는 것이 가장 효율적으로 앙상블을 확대시키는 방법으로 판단된다.
4. 요약 및 토의
본 연구에서는 기상청 기후예측시스템(GloSea5)의 과거 기후장 앙상블 확대 및 초기 시간에 따른 예측 성능과 앙상블 스프레드를 평가하였다. 이를 통해 국가 기상 슈퍼컴퓨터 5호기 도입 시점에 맞추어 전산 환경이 확충되는 경우 현업 시스템에서의 앙상블의 수를 늘리기 위한 최적의 앙상블 크기를 산정해 보고자 하였다. 추계적 기법을 이용하여 초기 시간당 3개의 과거 기후장 앙상블을 생산하고 있는 현재에서 14개까지 5배 가까이 증가시키는 실험을 진행하였으며, 계절 예측 평가를 위해 여름과 겨울철에 대하여 각 4개의 초기 시간을 조합하여 총 12개에서 56개까지의 앙상블을 확대하고 예측성능 개선 효과를 RMSE, ACC, 앙상블 스프레드와 RPC의 관점에서 평가하였다.
앙상블 수의 증가에 따라 위도별로는 모든 변수에서 변동성이 큰 영역에서 RMSE와 ACC 성능의 개선 폭이 크게 나타났고, RPC는 앙상블의 증가에 따라 1에 가까운 수준을 가지게 되었으며, 이는 상관계수의 증가보다는 노이즈 증가에 따른 signal-to-noise ratio 감소의 영향에서 온 것으로 판단되었다. RMSE/스프레드의 비 또한 점차 1에 가까워짐을 보여 보다 적절한 수준의 모델 스프레드를 가지기 위해서도 앙상블 확대가 필요함을 보였다.
최적의 앙상블 크기를 산정하기 위한 분석으로는 총 23개 영역에 대한 정규화된 ACC를 산출하였다. 정규화된 ACC 0.95 기준에서 최대 예측성능에 포화된다고 평가하였을 때, 전지구와 동아시아 영역에서는 강수량을 제외한 변수에 대하여 25~32개 앙상블을 필요로 하며, 강수량은 37개 이상의 앙상블을 필요로 함을 알 수 있었다. 초기 시간에 따른 예측성능 분석에서는 모든 앙상블을 이용한 경우보다 RMSE는 변수별로 가까운 1~3개, ACC는 대부분 가까운 2개의 초기 시간을 썼을 때 가장 예측에 유리함을 알 수 있어, 전산 자원량을 확보하고 초기 시간의 조합을 고려하여 적정 개수로 앙상블을 확대하는 것이 도움이 될 것으로 판단되었다.
현재까지 예측의 공백으로 여겨지고 있는 계절 내에서 계절 기간의 예측성능의 개선은 근본적으로는 모델의 물리-역학 과정 등의 꾸준한 개선으로 이어져야겠지만, 초기 시간과 앙상블에 의존하는 시스템의 특성상 시스템에 최적화된 앙상블과 초기장 개선이 아직까지는 예측성능의 개선을 이끌어 낼 수 있는 여지가 많은 것으로 보인다. 국가 기상 슈퍼컴퓨터 5호기가 새로이 도입되고, 현재 기상청 현업 기후예측시스템이 GloSea5에서 GloSea6로의 업그레이드를 준비하고 있는 시점에서, 본 연구에서의 앙상블의 확대 평가는 새로운 현업 기후예측시스템(GloSea6)에서의 앙상블 구성에 대한 근거로써도 활용될 것이다. 따라서 본 연구의 결과를 토대로 추후 과거기후장의 초기 시간을 2개로 줄이고 추계적 앙상블을 3개에서 7개로 확대시킬 예정이며, 예측장에 대해서도 앙상블 확대를 진행할 예정이다.
Acknowledgments
이 연구는 기상청 국립기상과학원 「기후예측 현업 시스템 개발」(KMA2018-00322)의 지원으로 수행되었습니다.
References
-
Adler, R. F., and Coauthors, 2003: The Version-2 Global Precipitation Climatology Project (GPCP) monthly precipitation analysis (1979-Present). J. Hydrometeor., 4, 1147-1167.
[https://doi.org/10.1175/1525-7541(2003)004<1147:TVGPCP>2.0.CO;2]

- Ahn, J.-B., J. Lee, and S. Jo, 2018: Evaluation of PNU CGCM ensemble forecast system for boreal winter temperature over South Korea. Atmosphere, 28, 509-520, (in Korean with English abstract).
-
Baker, L. H., L. C. Shaffrey, R. T. Sutton, A. Weisheimer, and A. A. Scaife, 2018: An intercomparison of skill and overconfidence/underconfidence of the wintertime North Atlantic Oscillation in multimodel seasonal forecasts. Geophys. Res. Lett., 45, 7808-7817.
[https://doi.org/10.1029/2018GL078838]

-
Bowler, N. E., A. Arribas, S. E. Beare, K. R. Mylne, and G. J. Shutts, 2009: The local ETKF and SKEB: Upgrades to the MOGREPS short-range ensemble prediction system. Q. J. R. Meteorol. Soc., 135, 767-776.
[https://doi.org/10.1002/qj.394]

-
Branković, Č., T. N. Palmer, F. Molteni, S. Tibaldi, and U. Cubasch, 1990: Extended-range predictions with ECMWF models: Time-lagged ensemble forecasting. Q. J. R. Meteorol. Soc., 116, 867-912.
[https://doi.org/10.1002/qj.49711649405]

-
Corti, S., A. Weisheimer, T. N. Palmer, F. J. Doblas-Reyes, and L. Magnusson, 2012: Reliability of decadal predictions. Geophys. Res. Lett., 39, L21712.
[https://doi.org/10.1029/2012GL053354]

- Dee, D. P., and Coauthors, 2011: The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc., 137, 553-597.
-
Dunstone, N., and Coauthors, 2020: Skilful interannual climate prediction from two large initialised model ensembles. Environ. Res. Lett., 15, 094083.
[https://doi.org/10.1088/1748-9326/ab9f7d]

-
Eade R., D. Smith, A. Scaife, E. Wallace, N. Dunstone, L. Hermanson, and N. Robinson, 2014: Do seasonal-to-decadal climate predictions underestimate the predictability of the real world?. Geophys. Res. Lett., 41, 5620-5628.
[https://doi.org/10.1002/2014GL061146]

-
Giorgi, F., and R. Francisco, 2000: Uncertainties in regional climate change prediction: a regional analysis of ensemble simulations with the HADCM2 coupled AOGCM. Climate Dyn., 16, 169-182.
[https://doi.org/10.1007/PL00013733]

-
Goddard, L., and Coauthors, 2012: A verification framework for interannual-to-decadal predictions experiments. Climate Dyn., 40, 245–272.
[https://doi.org/10.1007/s00382-012-1481-2]

- Hyun, Y.-K., J. Park, J. Lee, S. Lim, S.-I. Heo, H. Ham, S.-M. Lee, H.-S. Ji, and Y. Kim, 2020: Reliability assessment of temperature and precipitation seasonal probability in current climate prediction systems. Atmosphere, 30, 141-154, (in Korean with English abstract).
- Kim, S.-W., 2019: Optimal ensemble size for Sub-seasonal to Seasonal (S2S) prediction system. M. S. thesis, Dept. of Earth and Environmental Sciences, Seoul National University, 41 pp.
-
Kumar, A., A. G. Barnston, and M. P. Hoerling, 2001: Seasonal predictions, probabilistic verifications, and ensemble size. J. Climate, 14, 1671-1676.
[https://doi.org/10.1175/1520-0442(2001)014<1671:SPPVAE>2.0.CO;2]

-
MacLachlan, C., and Coauthors, 2015: Global Seasonal Forecast System version 5 (GloSea5): a high-resolution seasonal forecast system. Q. J. R. Meteorol. Soc., 141, 1072-1084.
[https://doi.org/10.1002/qj.2396]

-
Murphy, J. M., 1988: Assessment of the practical utility of extended range ensemble forecasts. Q. J. R. Meteorol. Soc., 116, 89-125.
[https://doi.org/10.1002/qj.49711649105]

-
Müller, W. A., C. Appenzeller, F. J. Doblas-Reyes, and M. A. Liniger, 2005: A debiased ranked probability skill score to evaluate probabilistic ensemble forecasts with small ensemble sizes. J. Climate, 18, 1513-1523.
[https://doi.org/10.1175/JCLI3361.1]

- Palmer, T., R. Buizza, R. Hagedorn, A. Lawrence, M. Leutbecher, and L. Smith, 2006: Ensemble prediction: a pedagogical perspective. ECMWF Newsletter, 106, 10-17.
-
Raynaud, L., and F. Bouttier, 2017: The impact of horizontal resolution and ensemble size for convective-scale probabilistic forecasts. Q. J. R. Meteorol. Soc., 143, 3037-3047.
[https://doi.org/10.1002/qj.3159]

-
Richardson, D. S., 2001: Measures of skill and value of ensemble prediction systems, their interrelationship and the effect of ensemble size. Q. J. R. Meteorol. Soc., 127, 2473-2489.
[https://doi.org/10.1002/qj.49712757715]

-
Rodwell, M. J., and F. J. Doblas-Reyes, 2006: Medium-range, monthly, and seasonal prediction for Europe and the use of forecast information. J. Climate, 19, 6025-6046.
[https://doi.org/10.1175/JCLI3944.1]

-
Scaife, A. A., and Coauthors, 2014: Skillful long-range prediction of European and North American winters. Geophys. Res. Lett., 41, 2514-2519.
[https://doi.org/10.1002/2014GL059637]

-
Smith, D. M., and Coauthors, 2020: North Atlantic climate far more predictable than models imply. Nature, 583, 796-800.
[https://doi.org/10.1038/s41586-020-2525-0]

-
Strommen, K., and T. N. Palmer, 2019: Signal and noise in regime systems: A hypothesis on the predictability of the North Atlantic Oscillation. Q. J. R. Meteorol. Soc., 145, 147-163.
[https://doi.org/10.1002/qj.3414]

- Talagrand, O., R. Vautard, and B. Strauss, 1997: Evaluation of probabilistic prediction systems. Proc., Workshop on Predictability, Shinfield Park, Reading, UK, ECMWF, 1-25.
-
Vitart, F., 2017: Madden - Julian Oscillation prediction and teleconnections in the S2S database. Q. J. R. Meteorol. Soc., 143, 2210-2220.
[https://doi.org/10.1002/qj.3079]

-
Williams, R. M., C. A. T. Ferro, and F. Kwasniok, 2013: A comparison of ensemble post-processing methods for extreme events. Q. J. R. Meteorol. Soc., 140, 1112-1120.
[https://doi.org/10.1002/qj.2198]

-
Weisheimer, A., D. Decremer, D. MacLeod, C. O'Reilly, T. N. Stockdale, S. Johnson, and T. N. Palmer, 2019: How confident are predictability estimates of the winter North Atlantic Oscillation?. Q. J. R. Meteorol. Soc., 145, 140-159.
[https://doi.org/10.1002/qj.3446]