GloSea5 북반구 대기 원격상관패턴의 1~6주 주별 예측성능 검증
Abstract
Due to frequent occurrence of abnormal weather, the need to improve the accuracy of subseasonal prediction has increased. Here we analyze the performance of weekly predictions out to 6 weeks by GloSea5 climate model. The performance in circulation field from January 1991 to December 2010 is first analyzed at each grid point using the 500-hPa geopotential height. The anomaly correlation coefficient and mean-square skill score, calculated each week against the ECWMF ERA-Interim reanalysis data, illustrate better prediction skills regionally in the tropics and over the ocean and seasonally during winter. Secondly, we evaluate the predictability of 7 major teleconnection patterns in the Northern Hemisphere: North Atlantic Oscillation (NAO), East Atlantic (EA), East Atlantic/Western Russia (EAWR), Scandinavia (SCAND), Polar/Eurasia (PE), West Pacific (WP), Pacific-North American (PNA). Skillful predictability of the patterns turns out to be approximately 1~2 weeks. During summer, the EAWR and SCAND, which exhibit a wave pattern propagating over Eurasia, show a considerably lower skill than the other 5 patterns, while in winter, the WP and PNA, occurring in the Pacific region, maintain the skill up to 2 weeks. To account for the model’s bias in reproducing the teleconnection patterns, we measure the similarity between the teleconnection patterns obtained in each lead time. In January, the model’s teleconnection pattern remains similar until lead time 3, while a sharp decrease of similarity can be seen from lead time 2 in July.
Keywords:
S2S, weekly prediction, GloSea5 hindcast experiment, teleconnection patterns1. 서 론
단기예측과 계절예측의 사이에 해당하는 계절내 예측 구간은 기상/기후 예보에 있어 흥미로우며 도전적인 시간규모이다. 대기는 혼돈 상태이므로 초기 상태의 작은 오차도 크게 성장하여 일반적으로 2주 이상의 예측이 불가능한 것으로 알려져 있다(Lorenz, 1963). 또한 수치 기상예측 모델을 활용한 일기예보는 초기 조건에 민감하고 그 예측 성능은 시간에 따라 급격히 감소하므로 7~10일 이후 유의미한 예측 결과를 제공하기 힘들다(White et al., 2017). 해양과 같이 천천히 변화하는 기후 시스템의 영향을 받기에는 계절내 시간규모가 상대적으로 짧기 때문에 기후예측 모델로 계절내 예측을 하는 것은 더욱 어렵다(Vitart, 2014).
1~6주 후를 주별(weekly)로 예측하는 1개월 전망, 혹은 계절내(subseasonal) 기후 예측은 인간의 삶과 지역사회에 미치는 영향이 커서 사회적 수요가 높다. 최근 기후변화에 따른 한반도의 이상기후 현상이 빈번하게 발생하고 있어(Park and Suh, 2011) 사회·경제적 피해를 최소화하기 위해 계절내 시간규모에서 기상/기후 모델의 주별 예측성능을 높이는 데에 초점이 모아지고 있다(WMO, 2013). 계절내 예측은 공중보건, 재난예보, 물관리, 에너지 및 농업 분야 등에서 지속적으로 유용하게 사용할 수 있는 것으로 알려져 있어 많은 기관에서 예측성 검증 및 개선에 관해 지속적인 연구를 수행 하고 있다(White et al., 2017).
세계기상기구(World Meteorological Organization; 이하 WMO)는 예측 기술과 이해도를 향상시키기 위하여 계절내-계절(Subseasonal to Seasonal; 이하 S2S) 예측 프로젝트를 2013년부터 실행하였고, 그간의 성과와 중요성을 인정받아 2018년부터 2차 프로젝트가 진행 중이다. S2S 예측 프로젝트는 6개의 소주제를 선택하였는데, 그 중 하나가 원격상관(teleconnection)이다(http://s2sprediction.net/static/subproject). 대기의 원격상관패턴은 광대한 지리적 영역에 걸쳐 반복적으로 나타나는 대규모 대기 순환 구조이다. 이러한 현상은 지면/해양 경계 조건과의 상호작용을 통해 수 개월 혹은 경년 이상의 시간규모에서도 두드러진 진동을 보이기는 하지만(e.g., Häkkinen et al., 2011), 일반적으로 1~2주의 시간규모를 가지므로 S2S 프로젝트가 예측인자로서 주목하고 있다(Feldstein, 2000).
원격상관패턴은 근본적으로 내부 대기 역학에 따라 자연적으로 발생하며(Barnston and Livezey, 1987), 해양 등의 경계조건이나 외적 강제력에 의해 발생하기도 한다(e.g., Jin and Hoskins, 1995). 이 패턴들은 대기파와 제트기류의 패턴을 대규모로 변화시킬 뿐 아니라 광대한 지역에 걸쳐 온도, 강우량, 폭풍 트랙, 제트기류의 위치와 강도 등에 영향을 주며, 먼 거리에서 동시에 일어나는 비정상적인 기상/기후 패턴의 원인으로 지목된다(https://www.cpc.ncep.noaa.gov/data/teledoc/teleintro.shtml). 예를 들어, 1993~2003 동안 겨울철 북대서양진동(North Atlantic Oscillation; 이하 NAO)의 강한 양의 위상으로 인해 북유럽과 미국 동부지역의 겨울철 기온은 높았고, 캐나다는 극한 추위를 경험하였다(Yiou and Nojaj, 2004).
본 연구에서는 한국 기상청에서 운용 중인 계절예측 모델에 나타난 북반구 원격상관패턴의 계절내 예측성능을 살펴보고자 한다. 미 국립해양대기국의 기후예측센터(National Oceanic and Atmospheric Administration/Climate Prediction Center, NOAA/CPC)에서 정의한 10개의 북반구 중-고위도 원격상관패턴(https://www.cpc.ncep.noaa.gov/data/teledoc/telecontents.shtml) 중 계절에 관계없이 꾸준하게 발달하는 7개의 패턴에 대하여 예측성능을 분석하고자 하였다. 기후모형으로 한국 기상청이 현업에 운용하고 있는 전지구 계절 예측 시스템(Global Seasonal Forecast System, version 5, GloSea5; MacLachlan et al., 2015)을 선택하였다. GloSea5는 영국 기상청이 대기-해양-해빙-지면 결합 모형인 HadGEM3(Hadley Center Global Environmental Model, Version 3)를 기반으로 하여 계절예측을 목적으로 설계한 모델로서, 한국 기상청이 2013년 7월부터 현업에 도입, 운용하고 있다. 원격상관패턴 예측성능평가는 본 모형의 대기 주요 모드 예측성능에 대한 정보를 제공하며, 원격상관패턴을 활용한 통계예측모형(Yoo et al., 2018)과 비교 결합을 통하여 예측성능 향상 가능성을 제시할 수 있다. 또한 모형의 원격상관패턴 모의의 정확성, 편이(bias), 또는 신뢰도(reliability)에 대한 정보를 제공할 수 있다.
2장에서는 본 연구에서 사용된 자료와 예측성능을 평가하는 방법을 소개하였다. 3장에서 지역별 500-hPa 지위고도 예측성능 평가 결과를 시작으로 원격상관패턴을 정의하고 평가한 결과물들에 대한 분석 및 해석을 기술하였다. 4장에서 이 논문에 대한 요약과 결론으로 마무리하였다.
2. 자료 및 예측성능 측도
2.1 자료
대한민국 기상청으로부터 제공받은 GloSea5의 과거 모의실험(Hindcast experiment)을 분석하였다. 대기 대규모 순환장 및 북반구 원격상관패턴의 주별 예측성능 평가를 위하여 일평균 500-hPa 지위고도 자료가 사용되었다. GloSea5는 영국 기상청(UK Met Office)의 대기모형(Unified Model, UM), 해양모형(Nucleus for European Modelling of the Ocean, NEMO), 지면모형(Joint UK Land Environment Simulator, JULES), 그리고 해빙모형(The Los Alamos Sea Ice Model, CICE)으로 구성되어 있다. 각 모형의 해상도 및 참고문헌은 Table 1에 정리하였다(Maclachlan et al., 2015).
과거기후 모의실험은 1991년 1월부터 2010년 12월까지 총 20년 동안, 매달 1일, 9일, 17일, 25일 4회 초기화되어 각각 60일 동안 적분되었다. 실험은 초기장을 변화시킨 3개의 앙상블 멤버로 구성되었는데, 초기장과 모형의 불확실성을 고려하여 3개의 앙상블 멤버 평균값을 사용하였다. 또한 본 연구의 관심이 원격상관패턴과 같은 대규모 대기순환장에 있기 때문에 실험자료는 위/경도 2.5o의 수평 해상도로 쌍선형(bilinear) 내삽해 사용하였다.
모형의 예측성 평가를 위한 관측값으로 ECMWF(European Centre for Medium-Range Weather Forecasts) ERA-interim 재분석자료(Dee et al., 2011)의 월평균 및 일평균 500-hPa 지위고도 자료를 사용하였다. 북반구 기후 설명에 용이한 원격상관패턴을 생성하기 위하여 GloSea5 모의자료 기간 보다 긴, 1979년부터 2016년까지 38년의 월평균 자료를 사용했고, 예측성능 평가에는 모의자료와 동일한 기간에 대한 일평균 자료를 사용하였다. 재분석 자료 역시 과거 모의자료와 해상도를 통일하기 위하여 위/경도 2.5o로 내삽 후 사용하였다.
예측성능 평가는 주별로 이루어졌다. 선행 시간(lead time)은 예측 시점과 초기화 시점의 시간상 차이로서, 선행 시간 1은 모형적분의 초기화 시점부터 1주일까지의 평균을 의미한다(Johansson, 2007). 60일 동안 적분된 일별자료들을 이용하면 선행 시간 8까지 분석이 가능하지만, 6주 이후는 주별 예측성이 거의 동일하고 매우 낮기 때문에 선행 시간 1~6을 분석 기간으로 선택하였다. 이는 대한민국 기상청의 1개월 전망(https://www.weather.go.kr/weather/forecast/long-range1.jsp)과 미국 NOAA/CPC Week 3-4 Outlooks(https://www.cpc.ncep.noaa.gov/products/predictions/WK34/)의 예측 시간을 넉넉히 포함한다.
2.2 예측성능 측도
관측값으로 초기화된 모형이 장시간 적분되면 예측결과가 관측값으로부터 멀어지며, 특히 그 차이가 모형 내부 물리-역학 과정의 특성에 따라 구조적 편이(structural bias)를 보이는, 이른바 기후 표류(climate drift)가 나타난다(Gupta et al., 2013). 따라서 구조적 편이의 제거는 천천히 변화는 경계값에 대한 준평형 반응을 보다 정확하게 관찰할 수 있게 한다. 다만, 평균을 안정적으로 추정하기 위해서는 적당한 크기 이상의 자료수가 필요하다. 본 연구에서는 아래와 같은 보정식을 사용하여 구조적 편이를 제거하는 모형 편이 보정(Bias correction)을 수행하였다.
| (1) |
| (2) |
여기서 H와 O는 각각 예측값과 관측값을 의미한다. 또한 t는 선행시간으로 주별로 1부터 6까지의 값을 가지며, y는 각 해에 해당하는 인덱스이다. 즉, Hyt는 각 초기장에 따른 앙상블 평균된 주별 예측값을 의미한다. 와 는 각 선행시간 별, 연중날짜(day of year)별로 20년에 대하여 평균한 값을 의미한다(n = 20). 는 구조적 편이가 제거된 예측값이다. 구조 편이 제거 결과는 다음 장에서 설명하였다.
보정된 모델 자료와 관측값을 이용하여 이상상관계수(Anomaly Correlation Coefficient; 이하 ACC)와 평균-제곱근 예측성능지수(Mean-Square Skill Score; 이하 MSSS)를 구함으로써 모형의 주별 예측성능을 평가하였다. 두 검증 지수는 WMO에서 표준화한 지수들에 포함되며 다년 시간규모의 예측성 평가를 위해 제안된 진단기법이다(Goddard et al., 2013). 또한 다수의 선행 연구에서 계절 규모의 예측성 검증을 위해 자주 사용한 평가 방법이다(e.g., Jung et al., 2015; Choi et al., 2016).
| (3) |
ACC는 위의 식으로 계산할 수 있으며, 각 기호의 의미는 앞서 기술한 바와 동일하다. ACC는 관측과 모델이 갖는 선형 상관관계에 대한 예측성 진단 변수이다. 그 값이 1에 가까울수록 모델과 관측이 완전한 선형관계임을 의미하고, 선형 상관성이 없을 때 0의 값을 가지며, 반대로 모의할 때 −1의 값을 갖는다. 경험적으로 0.5 또는 0.6 이하로 떨어질 경우 종관규모에 유용한 예측성이 없다고 판단하며(e.g., Wilks, 2011; Owen and Hewson, 2018), 본 연구에서는 0.5를 기준값으로 하였다.
MSSS는 평균-제곱 오차(Mean-Square Error; 이하 MSE)를 이용해 구한다(Murphy, 1988).
| (4) |
| (5) |
| (6) |
ACC를 사용하여 다시 정리하면 그 의미가 좀더 분명하다.
| (7) |
| (8) |
| (9) |
MSSS는 예측과 관측이 선형 상관관계를 갖더라도 시간에 따른 경향성의 크기가 다를 때 발생하게 되는 조건부 편이(Conditional bias)를 고려하는 예측진단변수이며, 관측과 모형 사이의 분산 차이를 고려하지 못하는 ACC의 단점을 보완한다. MSSS는 1에서 음의 무한대까지의 값을 가지며 ACC와 마찬가지로 1에 가까울수록 예측성이 높고 음의 값을 가질 경우 예측성이 없다고 판단한다.
3. 주별 예측성능 평가 결과
3.1 지역별 500-hPa 지위고도 예측성능 평가
원격상관패턴 예측성능 평가에 앞서, 전지구의 각 지역별 대기 순환장 예측성능의 특징을 살펴보기 위하여 500-hPa 지위고도의 주별 예측성능을 평가하였다. 2장에서 소개된 바와 같이, 주별로 정의된 모형의 구조적 편이를 각 선행시간에 대하여 제거하였다(Fig. 1). 60oS-70oN 지역에 대하여 20년 자료 중 1월 1일에 초기화된 자료의 편이와 수정된 편이를 살펴보면(왼쪽 패널) 과거기후 모의자료의 편이(검은색 선)는 1주차부터 −12 m 정도의 과소모의된 값을 보인다. 모형의 과소모의 경향은 선행시간과 함께 증가하여 3주차 이후로 −18 m 정도의 값으로 수렴한다. 또한 각 해에서 얻어진 구조적 편이의 최댓값과 최솟값의 범위(회색 음영)를 보면, 그 정도가 선행 시간에 따라 최대 6~34 m 정도로 증가함을 볼 수 있다. 2장에서 제시된 보정식을 사용하여 편이 수정된 20년 평균된 편이(빨간색 선)는 모든 선행시간에 대하여 0으로 보정됨을 확인할 수 있다. 각 해의 편이간 분산(분홍색 음영)은 보정되지 않았다. 7월 1일에 초기화된 자료에 대하여 살펴보면(오른쪽 패널), 1월과 비슷한 모형의 과소모의(검은색 선) 경향과 편이 수정 결과(빨간색 선)를 확인할 수 있다. Figure 1는 1월 1일과 7월의 1일에 시작된 결과만을 제시하나 다른 날짜에 대하여도 비슷한 결론을 얻을 수 있다(보이지 않음).
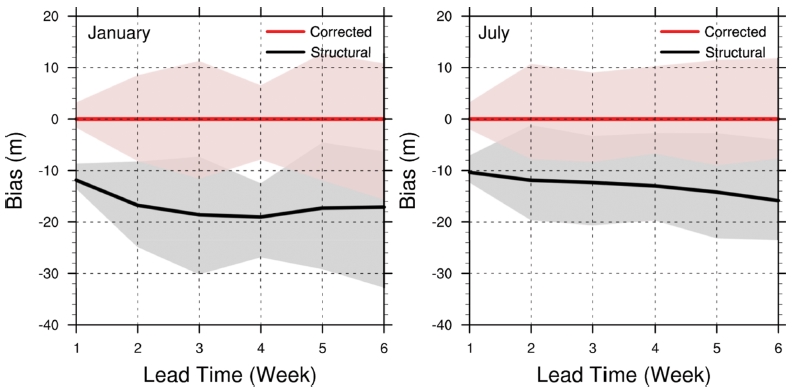
Black (red) line presents the 20-year average of the difference in the 60oS-70oN mean 500-hPa geopotential height between the hindcast raw data (bias-corrected data) and the ERA-interim data where the spread of the difference between the maximum and minimum values among the years is shown by grey (pink) shading. The results for an initial date of January 1 on the left and July 1 on the right.
북반구 겨울철의 전 지구 ACC, MSSS 값을 살펴보면 다음과 같은 특징들이 두드러진다(Figs. 2a, b). 첫째로 중고위도에 비하여 열대지역 예측성능이 초기 선행 시간에서부터 지속적으로 높게 유지된다. 이는 열대 지역이 ENSO (El Niño-Southern Oscillation)와 같이 천천히 변하는 강제력에 대한 반응으로 중층 지위고도에서 대규모적인 변동성이 작게 나타나는 것을 보여준다(Zhu et al., 2014). 반면에 중-고위도 지역은 초기에 존재하는 예측성능이 상대적으로 빠르게 제거됨을 확인할 수 있는데, 이는 중위도에서 강한 온도 경도로 인한 경압 불안정의 시간규모와 관련된 것으로 이해 가능하다(e.g., Eady, 1949). 또한 해양과 대륙의 열용량 차이 등에 의하여, 대륙지역을 중심으로 더욱 급격하게 예측성이 낮아짐을 확인할 수 있다.
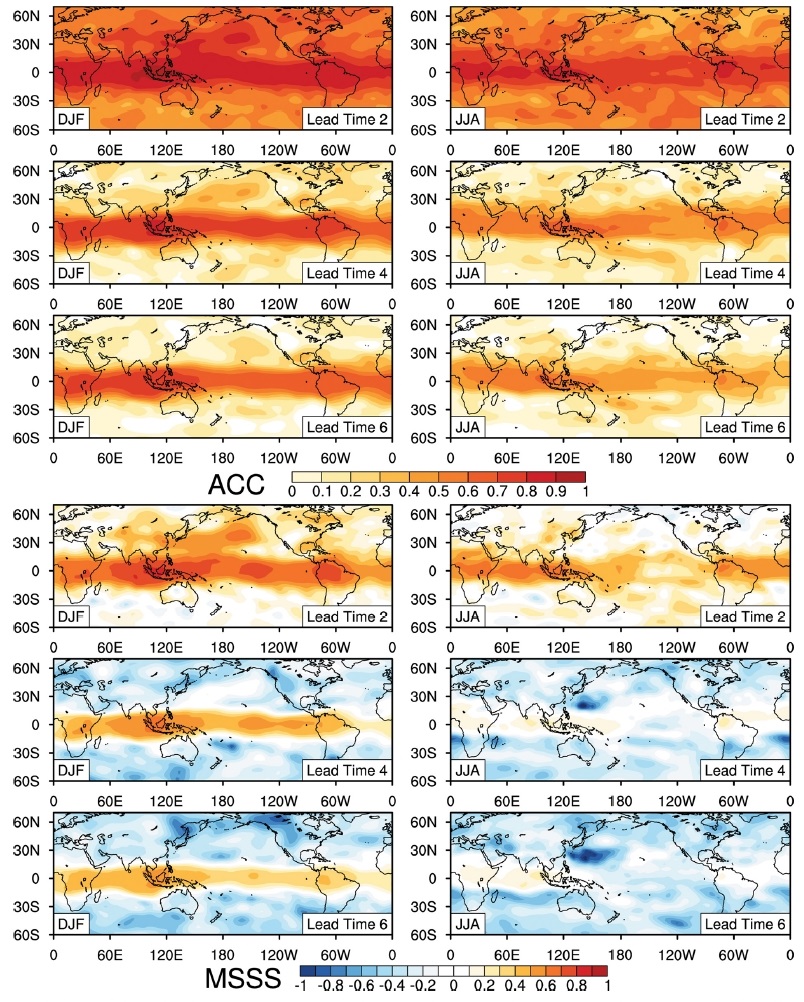
ACC and MSSS for the 500-hPa geopotential height from 60oS to 70oN for lead time 2, 4, and 6 (see bottom right of each figure) from December to February (DJF, left) and from June to August (JJA, right). The top six figures show the ACC value, and the bottom six figures show the MSSS value.
둘째로, 북반구 겨울철 예측성능이 여름철에 비해 높게 유지됨을 확인할 수 있다(Figs. 2c, d). 이는 기존 계절 시간규모 예측성능에서도 보고된 결과로, 남반구에 비하여 열대지역과 북반구에서 더욱 두드러진다. 북반구 겨울철에 대기 원격상관패턴과 열대 변동성인 매든줄리안진동(Madden Julian Oscillation; Madden and Julian 1971)이나 엘니뇨남방진동(El Niño-Southern Oscillation)의 지속성과 강도가 향상된다는 점과 일치한다. 위와 같은 열대 기후모드는 계절내 혹은 그 이상의 시간규모에서 준정기(quasi-periodic)적으로 변동하며, 로스비 파동 등을 통하여 그 영향이 중-고위도에 전파된다(e.g., Hoskins and Karoly, 1981; Seo and Son, 2012; Seo et al., 2016). 또한 여름철에 비하여 겨울철 강하게 발달하는 경압 시스템이 상대적으로 높은 예측성능에 기여할 수 있다. 남, 북반구 차이의 경우 북반구에서 상대적으로 우수한 초기 조건의 질과 지리적으로 고정된 강제력의 영향이 예측성능을 향상시킬 수 있다.
지역별 평균을 수행하여 ACC 결과(Fig. 3a)를 정량화하면, 열대 지역(20oS-20oN; 파란선)은 선행시간 4주차까지 ACC 기준 0.5를 넘는 반면, 북반구 중-고위도 지역(20oN-70oN; 초록선)은 선행시간 2주차까지만 유용한 예측성능(i.e., 0.5 이상)이 유지되는 것으로 계산되었다. 북반구 중-고위도의 대륙(빨간선)과 해양(주황선)을 나누어 ACC값을 평가하면, 해양의 예측성능이 3주차 이후에 대략 0.05~0.1 정도 높게 유지됨을 볼 수 있다. 북반구의 계절별 예측 결과를 살펴보면, 봄, 여름, 가을철에는 서로 비슷한 ACC를 보인 반면, 겨울철에는 선행시간 2주차부터 다른 세 계절에 비하여 0.05~0.1 정도 높은 ACC 값이 지속되었다(Fig. 3c). Figure 2에서 확인할 수 있듯 겨울철에 상대적으로 높은 ACC 값은 중고위도 해양과 대륙 위에서 모두 확인된다. 이는 대기의 장주기 변동성이 여름철보다 겨울철에 더 큰 강도를 보이며(Barnston and Livezey, 1987), 해양의 기후모드(e.g., Pacific Decadal Oscillation) 역시 그러하기 때문이다(Mills and Walsh, 2013).
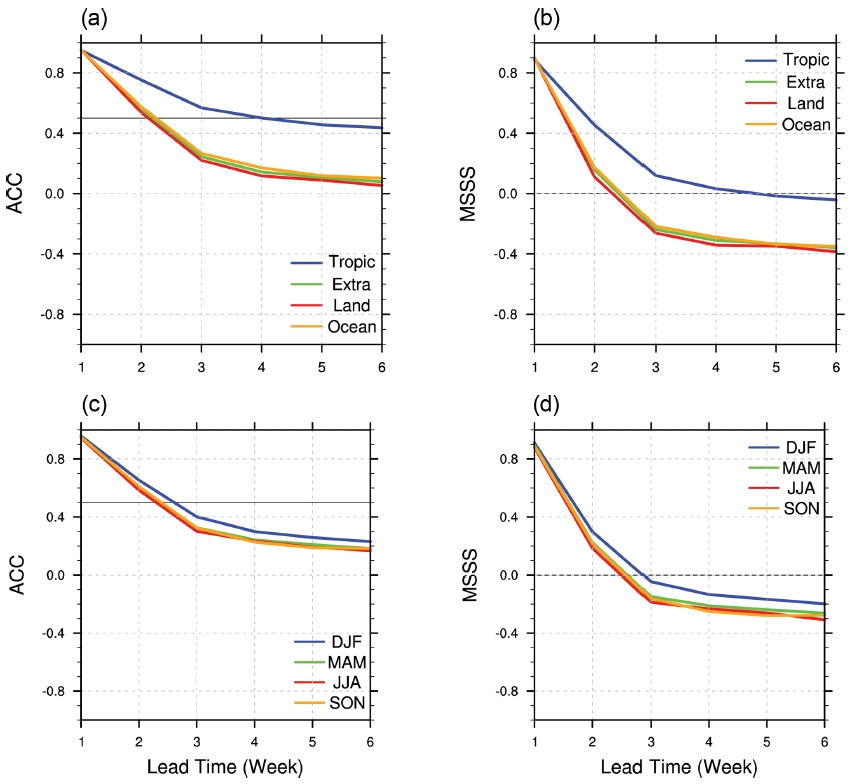
(a) ACC and (b) MSSS in the tropical (20oN-20oS, blue) and Northern Hemisphere (NH) extratropical regions (20-70oN, green) calculated for all months. In addition, the scores calculated separately for land (red) and ocean areas (orange) in the NH extratropics are also plotted. (c) ACC and (d) MSSS in the NH extratropics in each season: December to February (DJF, blue), March to May (MAM, green), June to August (JJA, red), and September to November (SON, orange).
MSSS 역시 ACC와 유사한 결과를 제시한다(Figs. 3b, d). 다시 말하면, 열대 지역이 중고위도 지역보다 예측성능이 높게 유지되며, 겨울철 예측성능이 타 계절에 비하여 높다. 앞서 설명하였듯, MSSS는 추가적으로 조건부 편이를 고려한 측도이기 때문에, MSSS와 ACC 간의 유사성은 관측값과 모형예측값 간의 분산의 기울기(Slope)가 1을 크게 벗어나지 않는 것을 의미한다.
3.2 원격상관패턴 정의
본 연구에서 원격상관패턴을 객관적으로 정의하기 위하여 NOAA/CPC의 정의를 따랐으며, 이는 Barnston and Livezey (1987)의 분석방법에 기반한다. 원격상관 패턴을 추출하기 위하여 북반구 지역(20oN-90oN) 월평균 500-hPa 지위고도 아노말리를 사용한다. 여기서 아노말리는 계절변동을 고려하여 월별 기후값을 제거한 것을 의미한다. 지위고도장을 먼저 10개의 경험적 직교함수(Empirical Orthogonal Function; 이하 EOF)로 필터링하며, 이후 하나의 요인에 높게 적재하는 변수의 수를 줄여서 요인의 해석에 중점을 둔 ‘Varimax’ 방식으로 회전된 경험적 직교함수(Rotated EOF; 이하 REOF)로 다시 정의한다. 각 패턴을 월별로 정의하는데, 월별 패턴을 위하여 앞뒤 1개월씩의 자료를 추가로 사용한다. 예를 들어, 1월 패턴은 12월부터 2월까지의 3개월 자료를 사용하여 정의한다. 인덱스는 각 월별 패턴에 일별 500-hPa 지위고도 아노말리를 내적한 후 월별 표준편차를 사용하여 표준화하였다.
REOF를 사용하여 객관적으로 정의된 원격상관패턴은 작용 중심(center of action)의 위치에 따라 명명된다. 본 연구에서 평가할 패턴은 대류권 중층에서 정의되는 NAO, EA (East Atlantic), EAWR (East Atlantic/Western Russia), SCAND (Scandinavia), PE(Polar/Eurasia), WP (West Pacific), PNA (Pacific-North American) 패턴이다(Fig. 4). NOAA/CPC는 이들에 추가로 북극 진동(Arctic Oscillation; 이하 AO), 남극 진동(Antarctic Oscillation; 이하 AAO) 등을 포함한 10개의 북반구 대기 원격상관패턴에 대해 월별 인덱스를 제공한다. 이 중 AAO는 남반구의 패턴이므로 분석에서 제외하였다.
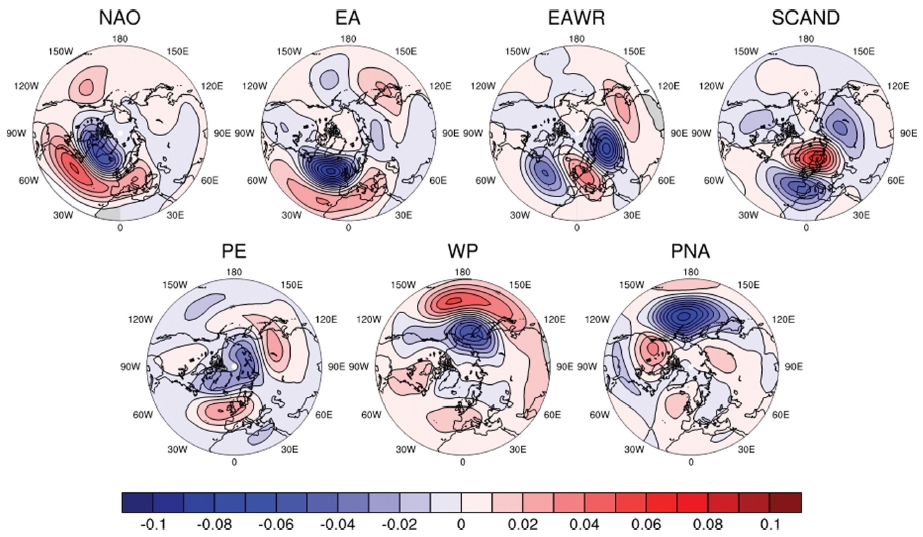
Dimensionless NH teleconnection patterns of 500-hPa geopotential height anomalies for NAO (North Atlantic Oscillation), EA (East Atlantic), EAWR (East Atlantic/Western Russia), SCAND (Scandinavia), PE (Polar/Eurasia), WP (West Pacific), and PNA (Pacific/North American) in January, obtained using ERA-interim. The contour interval is 0.01.
NAO 패턴은 남북 쌍극자 아노말리 센터로 구성된 것이 특징인데 한 곳은 그린란드에 위치하고 다른 한 곳은 북대서양의 중위도에 걸쳐 있다(Fig. 4). EA 패턴은 NAO 패턴에 비해 아노말리 중심이 남동쪽으로 밀려있으며, 두 패턴의 구조는 매우 유사하다. EAWR 패턴은 동부 대서양에서부터 서부 러시아에 걸쳐 3~4개의 주요 아노말리 센터로 구성된다. SCAND 패턴은 주요 순환 중심이 스칸디나비아 지역에 있고 반대의 약한 신호를 가진 센터가 서유럽과 동부 러시아/서부 몽골 지역에 걸쳐 있다. PE 패턴은 극 지역과 중국 북부 및 몽골에 대해 아노말리 센터가 존재하는 것이 특징이다. WP 패턴은 북태평양의 장주기 변동성의 주요 모드이며 캄차카 반도에 위치한 한 개의 중심과 남동 아시아와 서부 아열대 북태평양의 일부를 덮는 반대 신호의 중심을 포함하는 남북 쌍극자 형태를 하고 있다. PNA 패턴은 4개의 센터를 포함하는 특징이 있는데 하와이 부근과 북아메리카의 중간 산맥 지역에 같은 위상의 아노말리 센터가 존재하고, 알류샨 열도의 남부와 미국 남동부에 걸쳐 반대 위상의 아노말리 센터가 위치한다. 작용 중심만을 보고 패턴을 정의하기가 애매한 경우에는 NOAA/CPC의 월별 인덱스와의 상관계수를 고려하여 결정하였다.
3.3 원격상관패턴 예측성능 평가
500-hPa 지위고도를 사용했을 때 북반구 기후를 설명하는 원격상관패턴 중 가장 두드러진 NAO에 대하여, 계절별 NAO 패턴을 모델과 관측값에 각각 내적하였다. 예를 들어 겨울철의 경우 12월부터 2월까지의 자료에 그 중간에 해당하는 1월 NAO 패턴을 활용하며 여름철의 경우 6월부터 8월까지의 자료에 7월 패턴을 이용하여 내적한다. 내적한 결과에 대하여 상관성을 관찰할 수 있도록 4년 간(1993년 7월부터 1997년 7월까지)의 자료만을 시계열로 제시하였다(Fig. 5). 결과를 관찰할 시 주의할 점은, 모형이 매월 4번(1, 9, 17, 25일) 초기화 되는데, 그 주기가 일주일이 아니므로 각 선행 시간에 제시된 시계열이 서로 동일한 날짜에 해당하지 않는다. 관측값과 모형값의 상관계수(Fig. 5 각 패널 오른쪽 상단에 표기)는 전체 분석 기간인 20년에 대하여 계산되었다. 선행 시간 1주차 상관계수는 0.8이며, 4주차까지 그 값이 급격히 낮아지고(R = 0.17), 그 이후로 6주차까지 낮은 값을 유지한다. 관측값(빨간 점선)과 모형값(파란색 실선)이 제시하는 NAO 시계열의 주기(frequency)는 선행 시간이 지남에도 크게 다르지 않지만, 모형의 진폭은 선행 시간이 지날수록 다소 줄어드는 경향을 보인다. 진폭의 변화는 ACC에 영향을 주지 않지만, MSSS에는 영향을 미친다.
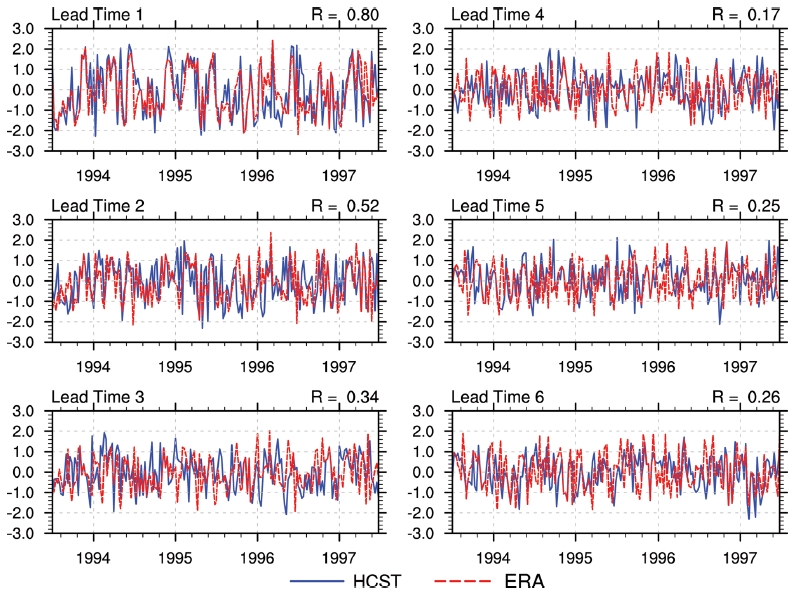
Time series of the NAO indices obtained for lead time 1-6 from the hindcasts (blue solid) and their corresponding time series from ERA-interim data (red dashed). The indices were constructed by projecting seasonal patterns (January, April, July, October) of NAO onto the 500-hPa geopotential height fields (20oN-90oN). The plotting period is from July 1993 to July 1997 to clearly see the relationship. R indicated at the top right of each panel represents the correlation coefficient between the two indices for the entire 20-year period.
NAO에 대한 ACC 결과를 정량화하면서 지상자료를 활용하여 북반구 기후에 가장 큰 영향을 주는 것으로 알려진 북극 진동(Arctic Oscillation; 이하 AO)에 대한 분석을 병행하였다. 선행 시간 2주차에서 ACC 기준 0.5를 초과한 인덱스가 없었으나(Figs. 6a, c), NAO는 겨울철(~0.5)은 다른 계절(0.2~0.4)보다 예측성이 높았다(Fig. 6a). MSSS 결과에서는 NAO는 여름을 제외한 계절에 대해서 선행 시간 1주까지만 유용한 예측성능(i.e., 0 이상)이 유지되는 것으로 계산되었다(Fig. 6b). AO는 전 계절에 대하여 선행 시간 1주까지 예측성능이 있는 것으로 나타났고 NAO와 마찬가지로 봄의 예측성능이 높았다(Fig. 6d). Feldstein(2000)이 일별 NAO 지수를 사용하여 파워 스펙트럼 분석법(Power spectrum analysis)으로 밝혀낸 NAO의 시간 규모는 9.5일이었고, Kushnir (2006)가 계절별 자기상관 분석을 통해 계산한 전계절 NAO e-folding 시간규모는 10일 미만이다. 이러한 결과를 고려할 때 NAO 예측성능은 Fig. 6에서 보이듯, 1~2주 정도라는 결론을 내릴 수 있다. 다만, NAO는 성층권 극소용돌이 등의 영향으로 강화될 수 있다는 점(Baldwin and Dunkerton, 2001)에서 추가적인 예측성능 확보가 가능하다.
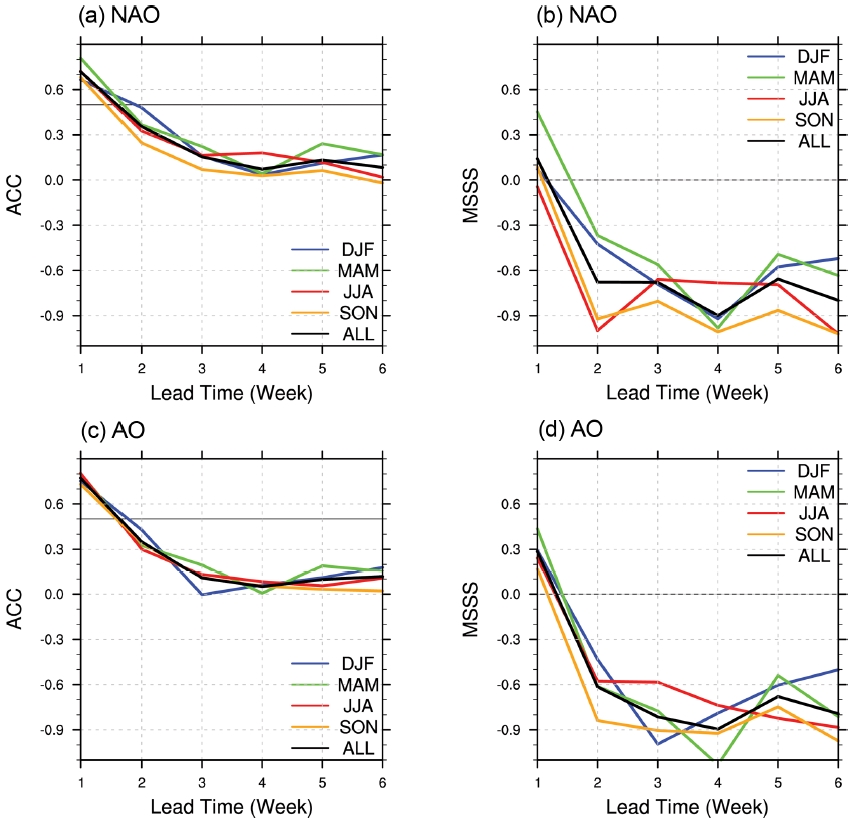
(a) ACC and (b) MSSS of the NAO index for DJF (blue), MAM (green), JJA (red), SON (orange), and all seasons (black). (c) ACC and (d) MSSS of the AO index were presented in the same way.
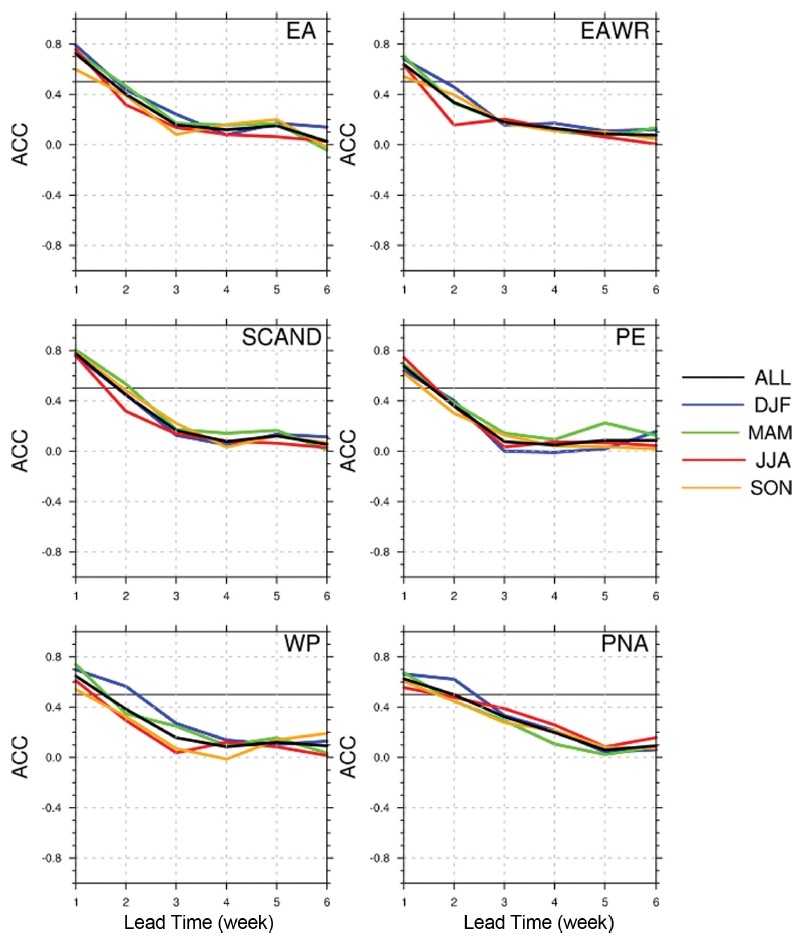
다른 원격상관패턴에 대한 ACC를 분석하면 다양한 해석이 가능하다(Fig. 7). 전 계절(검은색 선)에 대해서 선행 시간 1주차를 보면 SCAND (0.78), EA (0.72), PE (0.67), WP (0.65), EAWR (0.64), PNA (0.62) 순으로 예측성이 평가되었다. 선행 시간 2에서 ACC의 기준인 0.5를 넘는 인덱스는 PNA의 전 계절(0.50), SCAND 패턴의 봄철(0.53), WP 패턴의 겨울철(0.57)과 PNA 패턴의 겨울철(0.62)이었다. EAWR과 SCAND 패턴에 대해서 여름철 인덱스가 선행 시간 2주차에서 두드러지게 감소하고, 태평양에서 발생하는 두 가지 대표적인 원격상관 패턴인 WP와 PNA가 선행 시간 2주차에서 예측성이 좋은 인덱스로 판정된 것은 흥미로운 결과이다. 더욱이 SCAND, EAWR과 같은 원격상관 패턴은 북대서양에서 시작하여 유라시아를 넘어 동아시아로 향하는 파동의 형태를 갖는 패턴으로 동아시아 계절내 예측에 활용될 수 있다고 보고된 바 있다(Yoo et al., 2018). WP 역시 태평양 서쪽에 위치하여 동아시아 온도 변화에 중요한 영향을 준다(Park and Ahn, 2016).
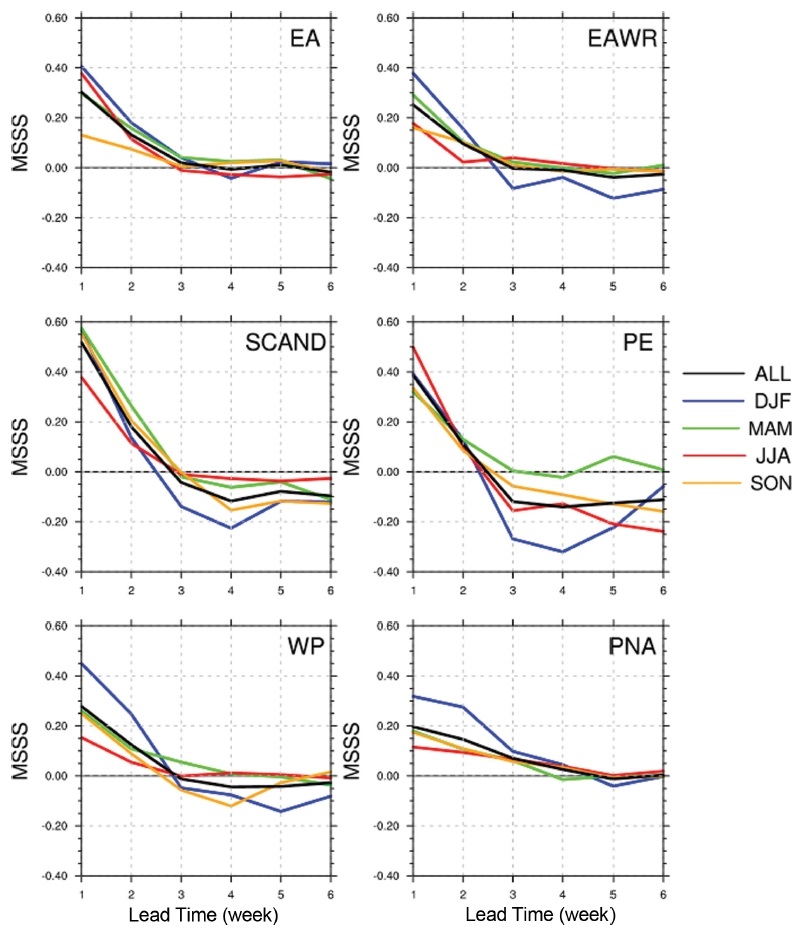
MSSS도 ACC와 유사한 결과를 제시하지만 조금 더 심층적인 분석을 가능하게 한다(Fig. 8). PE를 제외한 모든 패턴이 선행 시간 2주 전까지 겨울철(파란색 선) 예측 성능이 여름철(빨간색 선)에 비하여 높다. 태평양 지역에서 발생하는 패턴(WP, PNA)이 대서양이나 대륙 지역에서 발생하는 다른 원격상관 패턴들보다 겨울에 예측성이 높게 나타나는 특성을 좀더 명료하게 확인할 수 있다. PNA의 경우 열대태평양 ENSO에 대해 강제된 반응(forced response)으로 예측성능의 유지가 이해된다. WP의 경우도 해양과 결합된 North Pacific Oscillation으로도 정의가 가능하다는 점(Linkin and Nigam, 2008)에서 겨울철 예측성능 향상이 설명된다.
계절과 선행 시간에 따른 모형의 원격상관 예측성능을 좀 더 이해하기 위하여, 모형이 모사하는 NAO 1월과 7월 패턴의 변화 양상을 관찰하였다(Fig. 9). 선행 시간 1주에서 정의한 NAO 패턴을 기준으로 계산된 패턴 자기상관 계수를 오른쪽 상단에 표시했다. 상단의 그림 6개는 1월 NAO 패턴들로서 모두 0.90을 넘는 높은 상관계수를 보인다. 이는 모형이 선행 시간이 증가함에도 지속적으로 NAO 변동성 패턴을 잘 모사함을 의미한다. 하지만 7월의 경우(하단 그림 6개) 상관계수가 지속적으로 감소할 뿐만 아니라 쌍극 아노말리 센터 중 양의 위상이 선행 시간을 따라 희미해지며 선행 시간 4주차부터는 음의 위상이 북서태평양까지 퍼지는 듯한 모양 변화를 관찰할 수 있다. 이와 같은 결과는, 본 연구에서 수행된 바와 같이, 모형 고유 패턴을 활용하는 것이 정확한 NAO 예측성능 평가에 필요하다는 것을 제시한다. 모형 결과를 관측된 패턴에 내적(또는 투영, projection)하여 평가한다면, 특히 여름철, 예측성능을 과소모의할 수 있다.
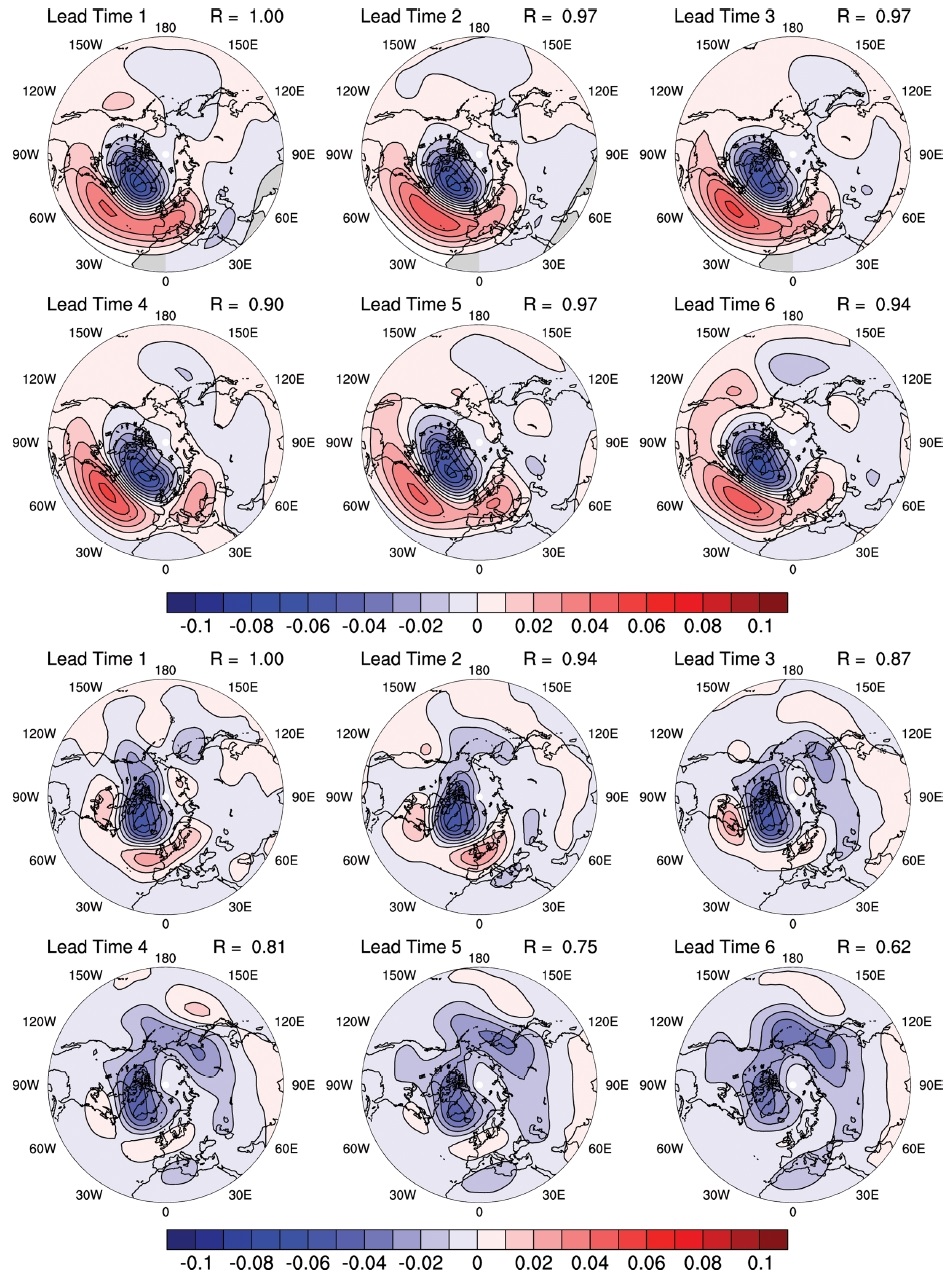
The NAO teleconnection patterns produced by using the hindcast results for lead time 1-6, respectively. The R value shown on the top right in each figure is the pattern correlation coefficient with the NAO pattern at lead time 1. The above six are in January, and the below six in July.
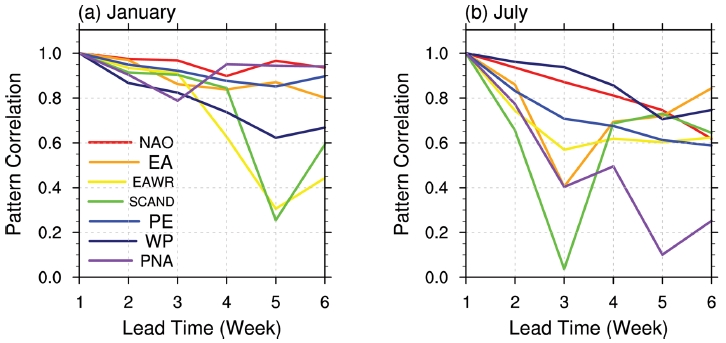
Figure 10은 NAO에 다른 6개의 원격상관패턴을 추가하여 Fig. 9에서와 마찬가지로 1월과 7월로 나누어 패턴 자기 상관계수를 구한 결과이다. 1월 패턴들은 선행 시간 2에서 상관계수가 전 패턴에 대하여 0.85를 초과하나, 7월에는 0.65까지 떨어지는 패턴이 발생한다. 선행 시간 3에는 1월 패턴들은 7개 모두 잘 추출되지만, 7월 패턴들 중 EA, PNA, SCAND 패턴들은 처음 패턴에 비해 크게 변형되는 것으로 보아 전반적으로 겨울철의 예측성이 좋다는 것을 뒷받침한다. 앞서 보았듯이, NAO 패턴(빨간색 선)은 1월에 비하여 7월에 선행 시간이 지남에 따라 자기상관계수가 선형적으로 감소한다. SCAND (초록색 선)와 EAWR (노란색 선)이 1월에는 선행 시간 5에서, 7월에는 3주차에 급감하는 것은 이 패턴들도 또한 겨울철의 예측성능이 더 높다는 것을 시사한다. PNA (Fig. 10 보라색 선)는 1월에는 상관계수가 항상 0.75를 넘지만 7월에는 3주차부터 0.5~0.1의 값을 보이며, 이는 PNA가 여름에 분간이 어려운 패턴으로 알려져 있는 것과 일치하는 결과이다. 그러나 WP는 Figs. 7, 8에서 여름철에 비해 겨울철에 선행시간 1~2주차까지 예측성이 두드러지게 좋았으나 패턴 분석에서는 여름철이 겨울철보다 전 구간에 대하여 예측성이 더 좋았다. 이는 모형에서 WP 패턴으로 추정되는 패턴이 관측값 혹은 NOAA/CPC에서 규정하는 패턴과 많이 달라서 발생하는 차이로 분석할 수 있다.
4. 요약 및 결론
GloSea5 기후모형의 계절내 시간규모의 예측성능을 향상시키기 위한 발판으로서, 원격상관패턴에 대해 예측성능을 분석하였다. 분석에 앞서 원격상관패턴 추출에 사용되는 500-hPa 지위고도 변수에 대하여 모형의 적분기간이 증가함에 따라 불가피하게 발생하는 구조적 편이를 제거한 후 예측성능을 평가하였다. 그 결과, 열대 지역에 대해서는 선행 시간 4까지 예측이 가능하지만 북반구 중-고위도 지역에 대해서는 2가 한계인 것으로 나타났다. 계절별로 분석하면 다른 계절에 비하여 겨울철의 예측성능이 더 높았다. 원격상관패턴을 추출하여 내적한 인덱스를 갖고 동일한 방식으로 분석하면, 선행 시간 2에서도 예측성능이 있다고 판단되는 패턴은 전 계절 PNA, 겨울철 PNA, 봄철 SCAND, 겨울철 WP였고, 나머지는 모두 1주 이내의 예측 성능을 갖는 것으로 분석되었다.
내적한 분석 결과물보다 정확하고 직관적인 분석이 가능하도록 모델이 각 선행 시간에 따라 원격상관 패턴을 어떻게 모의하는지 패턴 상관계수를 통해 살펴보았다. 1월 원격상관패턴들의 패턴 자기상관계수는 선행 시간 3까지 모든 패턴에 대하여 0.7 이상을 유지하였다. 7월에는 PNA, EAWR, SCAND 패턴의 상관계수가 급격히 감소함으로 인하여 선행 시간 2에서 0.6 이상을 보였다. 겨울철의 선행 시간 5에서 나타나는 EAWR, SCAND의 급격한 감소와 여름철 선행 시간 3에서 보여지는 SCAND, PNA, EA의 낮은 예측성을 통해 주별 예측 성능을 높일 수 있는 방향을 설정하는 데에 도움을 줄 것으로 기대한다.
계절 예측 시스템의 예측 기술의 지역적 차이에 대한 물리적 통찰력을 제공하기 위해 원격상관패턴이 발생하는 지역에 따라 WP, PNA/EA, NAO/SCAND, EAWR/PE 패턴을 분류하여 분석할 필요가 있다. 또한, 앙상블 개수를 늘려 다른 모델과의 분석을 시도하고, 결과에 대한 원인을 규명하기 위해 제트 기류의 출입구 위치와 강도, 로스비 파동의 영향 등을 고려한 해석이 향후 필요할 것으로 예상한다.
Acknowledgments
본 논문의 발전을 위해 귀중한 조언을 해주신 두 심사위원님께 감사드립니다. 본 연구는 한국연구재단(NRF-2019R1C1C1003161)의 지원으로 진행되었으며, GloSea5 자료는 대한민국 기상청으로부터 제공받아 연구되었습니다.
References
-
Baldwin, M. P., and T. J. Dunkerton, 2001: Stratospheric harbingers of anomalous weather regimes. Science, 294, 581-584.
[https://doi.org/10.1126/science.1063315]

-
Barnston, A. G., and R. E. Livezey, 1987: Classification, seasonality and persistence of low-frequency atmospheric circulation patterns. Mon. Wea. Rev., 115, 1083-1126.
[https://doi.org/10.1175/1520-0493(1987)115<1083:CSAPOL>2.0.CO;2]

-
Best, M. J., and Coauthors, 2011: The Joint UK Land Environment Simulator (JULES), model description-Part 1: energy and water fluxes. Geosci. Model Dev., 4, 677-699.
[https://doi.org/10.5194/gmd-4-677-2011]

-
Brown, A., S. Milton, M. Cullen, B. Golding, J. Mitchell, and A. Shelly, 2012: Unified modeling and prediction of weather and climate: A 25-year journey. Bull. Amer. Meteor. Soc., 93, 1865-1877.
[https://doi.org/10.1175/BAMS-D-12-00018.1]

-
Choi, J., S.-W. Son, Y.-G. Ham, J.-Y. Lee, and H.-M. Kim, 2016: Seasonal-to-interannual prediction skills of near-surface air temperature in the CMIP5 decadal hindcast experiments. J. Climate, 29, 1511-1527.
[https://doi.org/10.1175/JCLI-D-15-0182.1]

-
Dee, D. P., and Coauthors, 2011: The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc., 137, 553-597.
[https://doi.org/10.1002/qj.828]

-
Eady, E. T., 1949: Long Waves and Cyclone Waves. Tellus, 1, 33-52.
[https://doi.org/10.3402/tellusa.v1i3.8507]

-
Feldstein, S. B., 2000: The timescale, power spectra, and climate noise properties of teleconnection patterns. J. Climate, 13, 4430-4440.
[https://doi.org/10.1175/1520-0442(2000)013<4430:TTPSAC>2.0.CO;2]

-
Goddard, L., and Coauthors, 2013: A verification framework for interannual-to-decadal predictions experiments. Climate Dyn., 40, 245-272.
[https://doi.org/10.1007/s00382-012-1481-2]

-
Gupta, A. S., N. C. Jourdain, J. N. Brown, and D. Monselesan, 2013: Climate drift in the CMIP5 models. J. Climate, 26, 8597-8615.
[https://doi.org/10.1175/JCLI-D-12-00521.1]

-
Häkkinen, S., P. B. Rhines, and D. L. Worthen, 2011: Atmospheric blocking and Atlantic multidecadal ocean variability. Science, 334, 655-659.
[https://doi.org/10.1126/science.1205683]

-
Hoskins, B. J., and D. J. Karoly, 1981: The steady linear response of a spherical atmosphere to thermal and orographic forcing. J. Atmos. Sci., 38, 1179-1196.
[https://doi.org/10.1175/1520-0469(1981)038<1179:TSLROA>2.0.CO;2]

- Hunke, E. C., and W. H. Lipscomb, 2010: CICE: The Los Alamos sea ice model documentation and software user’s manual Version 4.1 LA-CC-06-012. Technical report, Los Alamos National Laboratory NM87545, 76 pp.
-
Jin, F., and B. J. Hoskins, 1995: The direct response to tropical heating in a baroclinic atmosphere. J. Atmos. Sci., 52, 307-319.
[https://doi.org/10.1175/1520-0469(1995)052<0307:TDRTTH>2.0.CO;2]

-
Johansson, Å., 2007: Prediction Skill of the NAO and PNA from Daily to Seasonal Time Scales. J. Climate, 20, 1957-1975.
[https://doi.org/10.1175/JCLI4072.1]

-
Jung, M.-I., S.-W. Son, J. Choi, and H.-S. Kang, 2015: Assessment of 6-month lead prediction skill of the GloSea5 hindcast experiment, Atmosphere, 25, 323-337, (in Korean with English abstract).
[https://doi.org/10.14191/Atmos.2015.25.2.323]

-
Kushnir, Y., W. A. Robinson, P. Chang, and A. W. Robertson, 2006: The physical basis for predicting atlantic sector seasonal-to-interannual climate variability. J. Climate, 19, 5949-5970.
[https://doi.org/10.1175/JCLI3943.1]

-
Lorenz, E. N., 1963: Deterministic Nonperiodic Flow. J. Atmos. Sci., 20, 130-141.
[https://doi.org/10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2]

-
MacLachlan, C., and Coauthors, 2015: Global Seasonal forecast system version 5 (GloSea5): a high-resolution seasonal forecast system. Q. J. R. Meteorol. Soc., 141, 1072-1084.
[https://doi.org/10.1002/qj.2396]

-
Madden, R. A., and P. R. Julian, 1971: Detection of a 40~50 day oscillation in the zonal wind in the tropical pacific. J. Atmos. Sci., 28, 702-708.
[https://doi.org/10.1175/1520-0469(1971)028<0702:DOADOI>2.0.CO;2]

- Madec, G., 2008: NEMO ocean engine. Note du Po?le de modélisation No.27 Institut Pierre-Simon Laplace (IPSL) France, 300 pp.
-
Mills, C. M., and J. E. Walsh, 2013: Seasonal variation and spatial patterns of the atmospheric component of the pacific decadal oscillation. J. Climate, 26, 1575-1594.
[https://doi.org/10.1175/JCLI-D-12-00264.1]

-
Murphy, A. H., 1988: Skill scores based on the mean square error and their relationships to the correlation coefficient. Mon. Wea. Rev., 116, 2417-2424.
[https://doi.org/10.1175/1520-0493(1988)116<2417:SSBOTM>2.0.CO;2]

-
Linkin, M. E., and S. Nigam, 2008: The North Pacific Oscillation-West Pacific teleconnection pattern: mature-phase structure and winter impacts. J. Climate, 21, 1979-1997.
[https://doi.org/10.1175/2007JCLI2048.1]

-
Owens, R. G., and T. D. Hewson, 2018: ECMWF Forecast User Guide. Reading, ECMWF.
[https://doi.org/10.21957/m1cs7h]

-
Park, H.-J., and J.-B. Ahn, 2016: Combined effect of the Arctic Oscillation and the Western Pacific pattern on East Asia winter temperature. Climate Dyn., 46, 3205-3221.
[https://doi.org/10.1007/s00382-015-2763-2]

- Park, W.-S., and M.-S. Suh, 2011: Characteristics and trends of tropical night occurrence in South Korea for recent 50 years (1958-2007). Atmosphere, 21, 361-371 (in Korean with English abstract).
-
Seo, K.-H., and S.-W. Son, 2012: The global atmospheric circulation response to tropical diabatic heating associated with the Madden-Julian oscillation during northern winter. J. Atmos. Sci., 69, 79-96.
[https://doi.org/10.1175/2011JAS3686.1]

-
Seo, K.-H., H.-J. Lee, and D. M. W. Frierson, 2016: Unraveling the teleconnection mechanisms that induce wintertime temperature anomalies over the Northern Hemisphere continents in response to the MJO. J. Atmos. Sci., 73, 3557-3571.
[https://doi.org/10.1175/JAS-D-16-0036.1]

-
Vitart, F., 2014: Evolution of ECMWF sub-seasonal forecast skill scores. Q. J. R. Meteorol. Soc., 140, 1889-1899.
[https://doi.org/10.1002/qj.2256]

-
Walters, D. N., and Coauthors, 2011: The Met Office Unified Model global atmosphere 3.0/3.1 and JULES global land 3.0/3.1 configurations. Geosci. Model Dev., 4, 919-941.
[https://doi.org/10.5194/gmd-4-919-2011]

- Wilks, D. S., 2011: Statistical methods in the atmospheric sciences. Vol. 100, Academic press, 676 pp.
-
White, C. J., and Coauthors, 2017: Potential applications of subseasonal-to-seasonal (S2S) predictions. Meteor. Appl., 24, 315-325.
[https://doi.org/10.1002/met.1654]

- WMO, 2012: Subseasonal to seasonal prediction - Research implementation plan. World Meteorological Organization, 66 pp [Available online at https://library.wmo.int/pmb_ged/subseasonal_to_seasonal_prediction-research_implementation_plan_2012.pdf, ].
-
Yiou, P., and M. Nogaj, 2004: Extreme climatic events and weather regimes over the North Atlantic: When and where? Geophys. Res. Lett., 31, L07202.
[https://doi.org/10.1029/2003GL019119]

-
Yoo, C., N. C. Johnson, C.-H. Chang, S. B. Feldstein, and Y.-H. Kim, 2018: Subseasonal prediction of wintertime East Asian temperature based on atmospheric teleconnections. J. Climate, 31, 9351-9366.
[https://doi.org/10.1175/JCLI-D-17-0811.1]

-
Zhu, H., M. C. Wheeler, A. H. Sobel, and D. Hudson, 2014: Seamless precipitation prediction skill in the tropics and extratropics from a global model. Mon. Wea. Rev., 142, 1556-1569.
[https://doi.org/10.1175/MWR-D-13-00222.1]